人教版数学七年级上册 1.2.1 有理数 教案
文档属性
| 名称 | 人教版数学七年级上册 1.2.1 有理数 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 178.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 22:29:57 | ||
图片预览




文档简介
第一章 有理数
1.2 有理数
1.2.1 有理数
一、教学目标
【知识与技能】
1.掌握有理数的概念,会对有理数按照一定的标准进行分类,培养分类能力;
2. 使学生会用正数、负数表示具有相反意义的量,并能按不同要求对有理数进行分类.
【过程与方法】
1.了解分类的标准与分类结果的相关性,初步了解“集合”的含义;
2. 经历对有理数进行分类探索的过程,初步感受分类讨论的数学思想.
【情感态度与价值观】
体验分类是数学上的常用处理问题的方法.
二、课型
新授课
三、课时
第1课时
四、教学重难点
【教学重点】
正确理解有理数的概念
【教学难点】
正确理解分类的标准和按照一定的标准进行分类.
五、课前准备
教师:课件、三角尺、有理数分类结构图等。
学生:三角尺、练习本、铅笔、圆珠笔或钢笔。
六、教学过程
(一)导入新课
某天毛毛看报纸,见到下面一段内容:冬季的一天,某地的最高气温为6℃,最低气温达到-10℃,平均气温是0℃,而同一天北京的气温-3℃~7℃,这里出现了哪些数?我们到目前为止学过了哪些数?你能试着将它们进行分类吗?今天我们要把大家学过的数进行分类命名.(出示课件2)
(二)探索新知
教师问1:在前两个学段,我们已经学习了很多不同类型的数,通过上两节课的学习,又知道了现在的数包括了负数,现在请同学们在草稿纸上任意写出3个数(同时请3个同学在黑板上写出).
学生板书回答:6,-2,0,0.5,20%,-,-20,,-0.76(答案不唯一)
教师问2:观察黑板上的9个数,并给它们进行分类.
学生回答:小数,正数,负数,分数,百分数等.
教师问3:0是正数还是负数?
学生回答:0既不是正数也不是负数.
教师问4:看上边的导入新课,这里面出现的数是什么数?
学生回答:6,7是正数; -10,-3是负数; 0既不是正数也不是负数.
教师问5:目前我们所学的小数有哪几类?(出示课件5)
学生回答:有限小数,无限循环小数,无限不循环小数.
教师问6:对于数5,可这样问:5和5. 1是相同的类型吗?
学生回答:不是.
教师问7:5可以表示5个人,而5. 1可以表示人数吗?
学生讨论后回答:(不可以)所以它们是不同类型的数,数5是正数中整个的数,我们就称它为“正整数”,而5. 1不是整个的数,称为“正分数,,.··…
教师问8:0.1, -0.5, 5.32, -1.5,0. 2,又是什么数?
学生回答:小数.
教师问9:这些小数可以化为分数吗?请动手试一试.
学生回答:可以,解答如下:
,,,,.
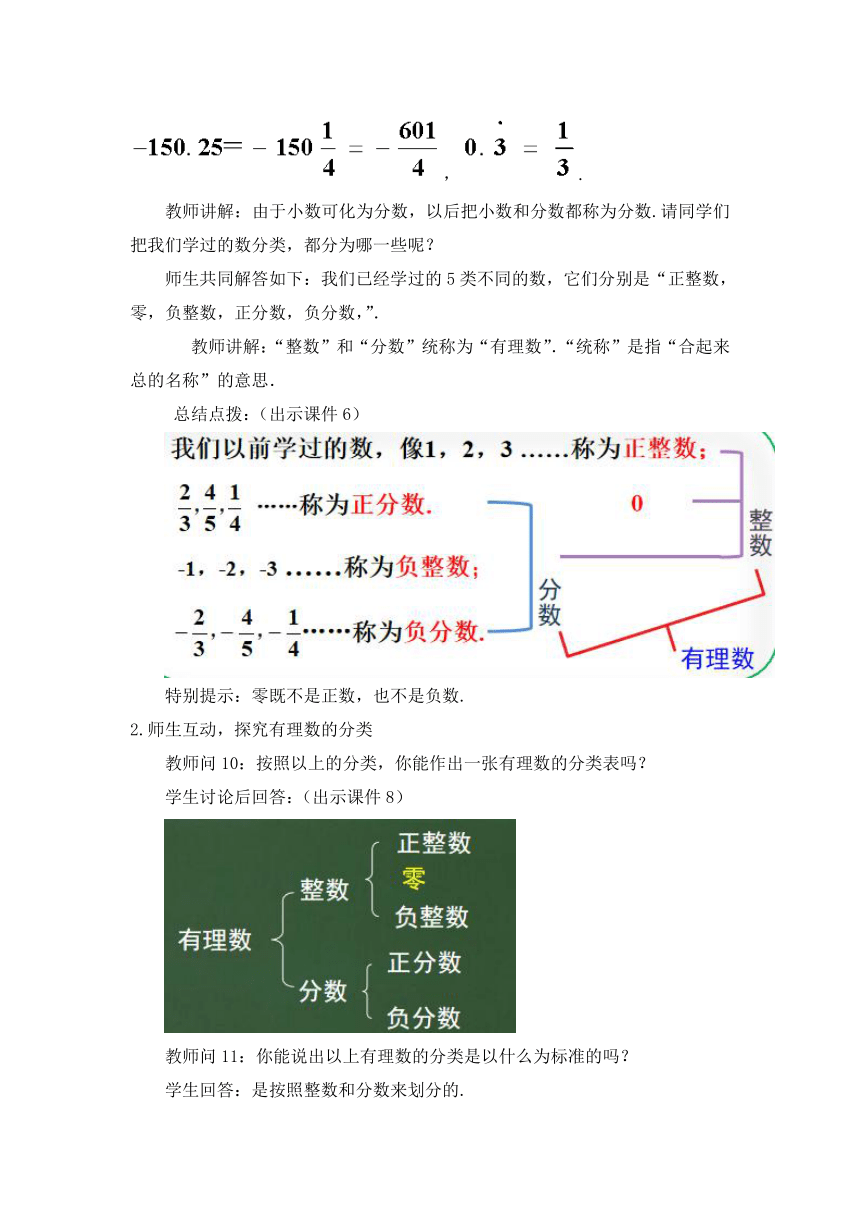
教师讲解:由于小数可化为分数,以后把小数和分数都称为分数.请同学们把我们学过的数分类,都分为哪一些呢?
师生共同解答如下:我们已经学过的5类不同的数,它们分别是“正整数,零,负整数,正分数,负分数,”.
教师讲解:“整数”和“分数”统称为“有理数”.“统称”是指“合起来总的名称”的意思.
总结点拨:(出示课件6)
特别提示:零既不是正数,也不是负数.
2.师生互动,探究有理数的分类
教师问10:按照以上的分类,你能作出一张有理数的分类表吗?
学生讨论后回答:(出示课件8)
教师问11:你能说出以上有理数的分类是以什么为标准的吗?
学生回答:是按照整数和分数来划分的.
教师问12:任意写出三个有理数,并说出是什么类型的数,与同伴进行交流.
学生回答:整数,分数,正整数,负整数,正分数,负分数.
教师向学生作如下的说明:把一些数放在一起,就组成了一个数的集合,简称“数集”,所有有理数组成的数集叫做有理数集.类似地,所有整数组成的数集叫做整数集,所有负数组成的数集叫做负数集……;
数集一般用圆圈或大括号表示,因为集合中的数是无限的,而在题中只填了所给的几个数,所以应该加上省略号.
教师问13:有理数可分为正数和负数两大类,对吗?为什么?
学生讨论后回答:不是,因为0既不是正数也不是负数.
教师问14:学了有理数的分类后,有没有一些数不是有理数呢?
师生共同讨论后解答如下:
有限小数和无限循环小数都是分数,所以也是有理数.
无限不循环小数(如π)不是分数,就不是有理数.
教师问15:有理数还有其他的分类方法吗?(出示课件10)
学生讨论后回答,教师参与讨论后得到如下共识:
注意:1. 如 能约分成整数的数不能(填“能”或“不能”)算做分数;
2. 无限不循环小数不是有理数,如π;
3. 整数中除了正整数和负整数,还有__0___.
总结点拨:(出示课件11)
有理数按符号(正、负)分类如下:
注意 :①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复;
③零是整数,但零既不是正数,也不是负数.
例1:下列说法:(出示课件13)
①0是整数;② 是负分数;
③4.2不是正数; ④自然数一定是正数;⑤负分数一定是负有理数.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
师生共同解答如下:
正确,②也正确,③4.2是正数,故错误,④0是自然数,但不是正数,故错误,⑤正确.所以答案选C
答案:C.
总结点拨:(出示课件15)
小学里学过的数除0外都是正数;正数前面添上“-”号的数是负数;0既不是正数,也不是负数,它表示正数、负数的界限.
有理数的分类方法不是唯一的,可以按整数和分数分成两大类,也可以按正有理数、零、负有理数分成三大类.
例2:把下列各数填在相应的集合中:(出示课件16)
正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负有理数集合:{ };
有理数集合:{ }.
师生共同解答如下:
解:正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负有理数集合:{ };
有理数集合:{ }.
总结点拨:1.像+300% 这种可以先化简成整数的数是整数不是分数;
2.π大于0是正数不是正有理数.
(三)课堂练习(出示课件18-31)
1.下列四个数中,是正整数的是( )
A.-1 B.0 C. D.1
2. 四个数-3, 0, 1, 2,其中负数是( )
A. -3 B. 0 C. 1 D. 2
3. 下列说法中,正确的是( )
A. 正整数、负整数统称为整数
B. 正分数、负分数统称为分数
C. 零既可以是正整数,也可以是负整数
D. 一个有理数不是正数就是负数
4. 下列各数:
-2,5, ,0.63,0,7,-0.05,-6,9, , .
其中正数有____个,负数有____个,正分数有____个,
负分数有____个,自然数有____个,整数有____个.
5. 判 断:
(1)0是整数.( )
(2)自然数一定是整数.( )
(3)0一定是正整数.( )
(4)整数一定是自然数.( )
6. 填空:
(1)有理数中,是整数而不是正数的是___________;
是负数而不是分数的是__________.
(2)零是_________,还是______,但不是_____,也不是_____.
7. 把下列各数分别填入相应的大括号里.
-15,+6,-2,-0.9,1, ,0, ,0.63,-4.95.
(1)正整数集合:{ …}
(2)负整数集合:{ …}
(3)正分数集合:{ …}
(4)负分数集合:{ …}
8. 某中学对九年级男生进行引体向上的测试,以能做10个为标准,超过的次数用正数表示,不足的次数用负数表示,其中8名男生的成绩如下:+2,-5,0,-2,+4,-1,-1,+3.
(1)达到标准的男生占百分之几
(2)他们共做了多少个引体向上
参考答案:
1.D
2.A
3.B
4.6;4;3;2;4;6.
5.(1)√ (2)√ (3)× (4)×
6.(1)负整数和0;负整数.(2)有理数;整数;正数;负数.
7. (1)正整数集合:{ +6,1 …}
(2)负整数集合:{ -15,-2 …}
(3)正分数集合:{ , ,0.63 …}
(4)负分数集合:{ -0.9,-4.95 …}
8. 解:(1) ,达到标准的男生占50%.
(2)2-5+0-2+4-1-1+3+8×10 = 80(个),他们共做了80个引体向上.
(四)课堂小结
今天我们学了哪些内容:
到现在为止我们学过的数都是有理数(圆周率除外),有理数可以按不同的标准进行分类,标准不同,分类的结果也不同。
(五)课前预习
预习下节课(1.2.2)的相关内容。
知道数轴的相关定义
七、课后作业
1、教材6到7页练习1,2
2、把下列各数填入相应的集合内.-10,8,-7,3,-10%,,2,0,3.14,-67,,0.618,-1,0.3080080008…
正数集合{ …};
负数集合{ …};
整数集合{ …};
分数集合{ …}.
八、板书设计:
1.到现在为止,我们学过的数(π 除外)都是有理数.
2.有理数的分类
3.注意0的特殊性,分类时不要遗漏0.
九、教学反思:
1,本课在引人了负数后对所学过的数按照一定的标准进行分类,提出了有理数的概
念.分类是数学中解决问题的常用手段,通过本节课的学习使学生了解分类的思想并进
行简单的分类是数学能力的体现,教师在教学中应引起足够的重视.关于分类标准与分
类结果的关系,分类标准的确定可向学生作适当的渗透,集合的概念比较抽象,学生真正接受需要很长的过程,本课不要过多展开。
2,本课具有开放性的特点,给学生提供了较大的思维空间,能促进学生积极主动地参加学习,亲自体验知识的形成过程,可避免直接进行分类所带来的枯燥性;同时还体现合作学习、交流、探究提高的特点,对学生分类能力的养成有很好的作用。
3,两种分类方法,应以第一种方法为主,第二种方法可视学生的情况进行。
1.2 有理数
1.2.1 有理数
一、教学目标
【知识与技能】
1.掌握有理数的概念,会对有理数按照一定的标准进行分类,培养分类能力;
2. 使学生会用正数、负数表示具有相反意义的量,并能按不同要求对有理数进行分类.
【过程与方法】
1.了解分类的标准与分类结果的相关性,初步了解“集合”的含义;
2. 经历对有理数进行分类探索的过程,初步感受分类讨论的数学思想.
【情感态度与价值观】
体验分类是数学上的常用处理问题的方法.
二、课型
新授课
三、课时
第1课时
四、教学重难点
【教学重点】
正确理解有理数的概念
【教学难点】
正确理解分类的标准和按照一定的标准进行分类.
五、课前准备
教师:课件、三角尺、有理数分类结构图等。
学生:三角尺、练习本、铅笔、圆珠笔或钢笔。
六、教学过程
(一)导入新课
某天毛毛看报纸,见到下面一段内容:冬季的一天,某地的最高气温为6℃,最低气温达到-10℃,平均气温是0℃,而同一天北京的气温-3℃~7℃,这里出现了哪些数?我们到目前为止学过了哪些数?你能试着将它们进行分类吗?今天我们要把大家学过的数进行分类命名.(出示课件2)
(二)探索新知
教师问1:在前两个学段,我们已经学习了很多不同类型的数,通过上两节课的学习,又知道了现在的数包括了负数,现在请同学们在草稿纸上任意写出3个数(同时请3个同学在黑板上写出).
学生板书回答:6,-2,0,0.5,20%,-,-20,,-0.76(答案不唯一)
教师问2:观察黑板上的9个数,并给它们进行分类.
学生回答:小数,正数,负数,分数,百分数等.
教师问3:0是正数还是负数?
学生回答:0既不是正数也不是负数.
教师问4:看上边的导入新课,这里面出现的数是什么数?
学生回答:6,7是正数; -10,-3是负数; 0既不是正数也不是负数.
教师问5:目前我们所学的小数有哪几类?(出示课件5)
学生回答:有限小数,无限循环小数,无限不循环小数.
教师问6:对于数5,可这样问:5和5. 1是相同的类型吗?
学生回答:不是.
教师问7:5可以表示5个人,而5. 1可以表示人数吗?
学生讨论后回答:(不可以)所以它们是不同类型的数,数5是正数中整个的数,我们就称它为“正整数”,而5. 1不是整个的数,称为“正分数,,.··…
教师问8:0.1, -0.5, 5.32, -1.5,0. 2,又是什么数?
学生回答:小数.
教师问9:这些小数可以化为分数吗?请动手试一试.
学生回答:可以,解答如下:
,,,,.
教师讲解:由于小数可化为分数,以后把小数和分数都称为分数.请同学们把我们学过的数分类,都分为哪一些呢?
师生共同解答如下:我们已经学过的5类不同的数,它们分别是“正整数,零,负整数,正分数,负分数,”.
教师讲解:“整数”和“分数”统称为“有理数”.“统称”是指“合起来总的名称”的意思.
总结点拨:(出示课件6)
特别提示:零既不是正数,也不是负数.
2.师生互动,探究有理数的分类
教师问10:按照以上的分类,你能作出一张有理数的分类表吗?
学生讨论后回答:(出示课件8)
教师问11:你能说出以上有理数的分类是以什么为标准的吗?
学生回答:是按照整数和分数来划分的.
教师问12:任意写出三个有理数,并说出是什么类型的数,与同伴进行交流.
学生回答:整数,分数,正整数,负整数,正分数,负分数.
教师向学生作如下的说明:把一些数放在一起,就组成了一个数的集合,简称“数集”,所有有理数组成的数集叫做有理数集.类似地,所有整数组成的数集叫做整数集,所有负数组成的数集叫做负数集……;
数集一般用圆圈或大括号表示,因为集合中的数是无限的,而在题中只填了所给的几个数,所以应该加上省略号.
教师问13:有理数可分为正数和负数两大类,对吗?为什么?
学生讨论后回答:不是,因为0既不是正数也不是负数.
教师问14:学了有理数的分类后,有没有一些数不是有理数呢?
师生共同讨论后解答如下:
有限小数和无限循环小数都是分数,所以也是有理数.
无限不循环小数(如π)不是分数,就不是有理数.
教师问15:有理数还有其他的分类方法吗?(出示课件10)
学生讨论后回答,教师参与讨论后得到如下共识:
注意:1. 如 能约分成整数的数不能(填“能”或“不能”)算做分数;
2. 无限不循环小数不是有理数,如π;
3. 整数中除了正整数和负整数,还有__0___.
总结点拨:(出示课件11)
有理数按符号(正、负)分类如下:
注意 :①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复;
③零是整数,但零既不是正数,也不是负数.
例1:下列说法:(出示课件13)
①0是整数;② 是负分数;
③4.2不是正数; ④自然数一定是正数;⑤负分数一定是负有理数.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
师生共同解答如下:
正确,②也正确,③4.2是正数,故错误,④0是自然数,但不是正数,故错误,⑤正确.所以答案选C
答案:C.
总结点拨:(出示课件15)
小学里学过的数除0外都是正数;正数前面添上“-”号的数是负数;0既不是正数,也不是负数,它表示正数、负数的界限.
有理数的分类方法不是唯一的,可以按整数和分数分成两大类,也可以按正有理数、零、负有理数分成三大类.
例2:把下列各数填在相应的集合中:(出示课件16)
正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负有理数集合:{ };
有理数集合:{ }.
师生共同解答如下:
解:正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负有理数集合:{ };
有理数集合:{ }.
总结点拨:1.像+300% 这种可以先化简成整数的数是整数不是分数;
2.π大于0是正数不是正有理数.
(三)课堂练习(出示课件18-31)
1.下列四个数中,是正整数的是( )
A.-1 B.0 C. D.1
2. 四个数-3, 0, 1, 2,其中负数是( )
A. -3 B. 0 C. 1 D. 2
3. 下列说法中,正确的是( )
A. 正整数、负整数统称为整数
B. 正分数、负分数统称为分数
C. 零既可以是正整数,也可以是负整数
D. 一个有理数不是正数就是负数
4. 下列各数:
-2,5, ,0.63,0,7,-0.05,-6,9, , .
其中正数有____个,负数有____个,正分数有____个,
负分数有____个,自然数有____个,整数有____个.
5. 判 断:
(1)0是整数.( )
(2)自然数一定是整数.( )
(3)0一定是正整数.( )
(4)整数一定是自然数.( )
6. 填空:
(1)有理数中,是整数而不是正数的是___________;
是负数而不是分数的是__________.
(2)零是_________,还是______,但不是_____,也不是_____.
7. 把下列各数分别填入相应的大括号里.
-15,+6,-2,-0.9,1, ,0, ,0.63,-4.95.
(1)正整数集合:{ …}
(2)负整数集合:{ …}
(3)正分数集合:{ …}
(4)负分数集合:{ …}
8. 某中学对九年级男生进行引体向上的测试,以能做10个为标准,超过的次数用正数表示,不足的次数用负数表示,其中8名男生的成绩如下:+2,-5,0,-2,+4,-1,-1,+3.
(1)达到标准的男生占百分之几
(2)他们共做了多少个引体向上
参考答案:
1.D
2.A
3.B
4.6;4;3;2;4;6.
5.(1)√ (2)√ (3)× (4)×
6.(1)负整数和0;负整数.(2)有理数;整数;正数;负数.
7. (1)正整数集合:{ +6,1 …}
(2)负整数集合:{ -15,-2 …}
(3)正分数集合:{ , ,0.63 …}
(4)负分数集合:{ -0.9,-4.95 …}
8. 解:(1) ,达到标准的男生占50%.
(2)2-5+0-2+4-1-1+3+8×10 = 80(个),他们共做了80个引体向上.
(四)课堂小结
今天我们学了哪些内容:
到现在为止我们学过的数都是有理数(圆周率除外),有理数可以按不同的标准进行分类,标准不同,分类的结果也不同。
(五)课前预习
预习下节课(1.2.2)的相关内容。
知道数轴的相关定义
七、课后作业
1、教材6到7页练习1,2
2、把下列各数填入相应的集合内.-10,8,-7,3,-10%,,2,0,3.14,-67,,0.618,-1,0.3080080008…
正数集合{ …};
负数集合{ …};
整数集合{ …};
分数集合{ …}.
八、板书设计:
1.到现在为止,我们学过的数(π 除外)都是有理数.
2.有理数的分类
3.注意0的特殊性,分类时不要遗漏0.
九、教学反思:
1,本课在引人了负数后对所学过的数按照一定的标准进行分类,提出了有理数的概
念.分类是数学中解决问题的常用手段,通过本节课的学习使学生了解分类的思想并进
行简单的分类是数学能力的体现,教师在教学中应引起足够的重视.关于分类标准与分
类结果的关系,分类标准的确定可向学生作适当的渗透,集合的概念比较抽象,学生真正接受需要很长的过程,本课不要过多展开。
2,本课具有开放性的特点,给学生提供了较大的思维空间,能促进学生积极主动地参加学习,亲自体验知识的形成过程,可避免直接进行分类所带来的枯燥性;同时还体现合作学习、交流、探究提高的特点,对学生分类能力的养成有很好的作用。
3,两种分类方法,应以第一种方法为主,第二种方法可视学生的情况进行。
