七年级数学上册同步精品课件(沪科版)1.2.1 数轴 课件-(共25张PPT)
文档属性
| 名称 | 七年级数学上册同步精品课件(沪科版)1.2.1 数轴 课件-(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 480.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
1.2.1 数轴
注意:有理数可以按整数和分数来分类;
也可以按照正有理数、负有理数 和 0 来分类,
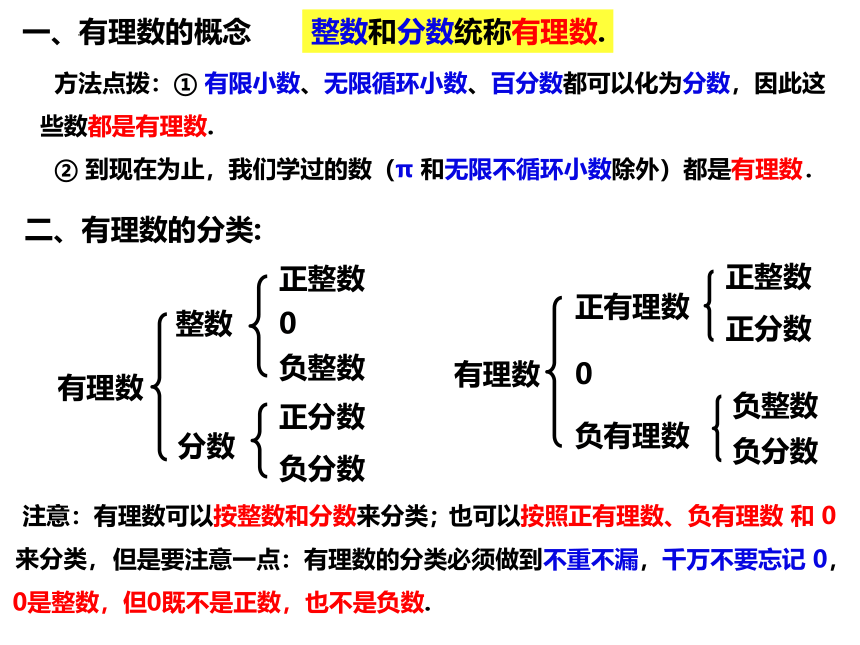
一、有理数的概念
二、有理数的分类:
整数和分数统称有理数.
方法点拨:① 有限小数、无限循环小数、百分数都可以化为分数,因此这些数都是有理数.
② 到现在为止,我们学过的数(π 和无限不循环小数除外)都是有理数.
有理数
整数
分数
正整数
0
负整数
正分数
负分数
有理数
正有理数
负有理数
0
正整数
正分数
负整数
负分数
有理数的分类必须做到不重不漏,千万不要忘记 0,0是整数,但0既不是正数,也不是负数.
但是要注意一点:
B
A
C
(3) 温度计刻度的正负是怎样规定的?以什么为基准?基准刻度线表示多少摄氏度?
情境引入
问题一:观察如图的温度计,回答下列问题:
(1) 点A表示多少摄氏度?点B呢?点C呢?
在0℃以上为正,0℃以下为负,温度计是以0℃为基准的.
(4) 每摄氏度两条刻度线之间的距离有什么特点
距离相等
(2) A,B,C三点所表示的温度哪个高?哪个低?
0℃
20℃
-5℃
A点所表示的温度最高,B点所表示的温度最低.
情境引入
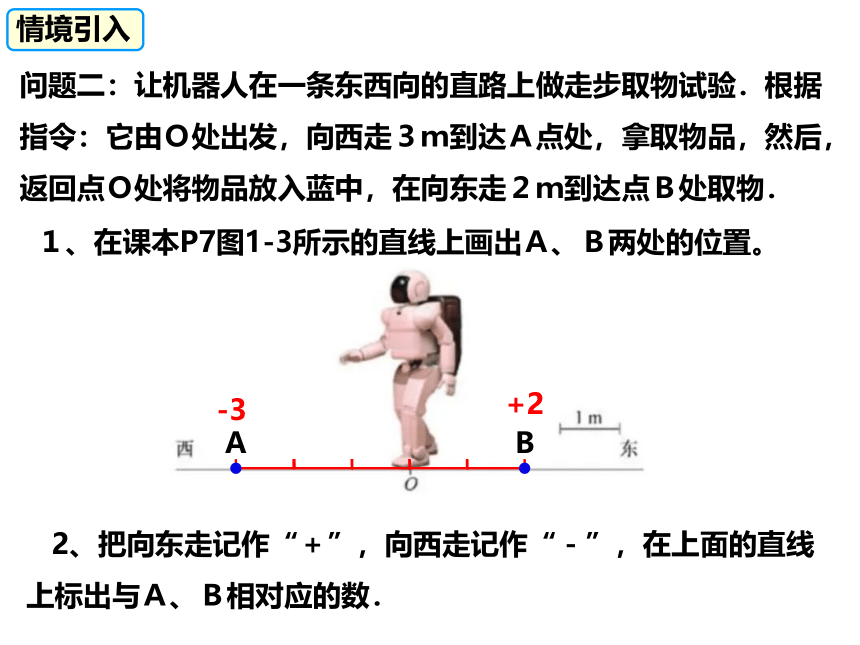
问题二:让机器人在一条东西向的直路上做走步取物试验.根据指令:它由O处出发,向西走3m到达A点处,拿取物品,然后,返回点O处将物品放入蓝中,在向东走2m到达点B处取物.
1、在课本P7图1-3所示的直线上画出A、B两处的位置。
2、把向东走记作“+”,向西走记作“-”,在上面的直线上标出与A、B相对应的数.
A
B
-3
+2
探究新知
思考:根据前面的两个问题,你能用一条直线上的点表示有理数吗?
在直线上从原点向右,每隔一个单位长度取一点,这些点依次表示1,2,3,4
,......,
(当直线水平放置时,一般取从左到右的方向为正方向,并用箭头表示),
探究新知
下面,我们来学习用直线上的点来表示数.
第一步:画一条直线,在这条直线上任取一点,叫做原点,
0
第二步:规定这条直线的一个方向为正方向
相反
第三步:适当地选取某一长度作为单位长度,
从原点向左,每隔一个单位长度取一点,他们依次表示 -1,-2,-3,-4,...... ;
用这点表示数0.
的方向就是负方向。
1
2
3
4
-1
-2
-3
-4
同一数轴上的单位长度必须相同.
概念学习
0
1
2
3
4
-1
-2
-3
-4
像这样规定了原点、正方向和单位长度的直线叫做数轴.
数轴定义包含三层含义:
① 数轴是一条直线,它可以向两端无限延伸
正方向
② 数轴的三要素
原点
单位长度
三者缺一不可
③ 原点的选定、正方向的选取、单位长度大小的确定,都是根据实际需要“选定”的.
概念学习
0
1
2
3
4
-1
-2
-3
-4
像这样规定了原点、正方向和单位长度的直线叫做数轴.
画数轴的步骤:
一画:画一条直线 (一般画成水平的直线);
二取:在这条直线的适当位置取一点作为原点,用0表示;
三定:确定正方向,并用箭头表示.
四选:根据需要选取适当单位长度,并标上数字.
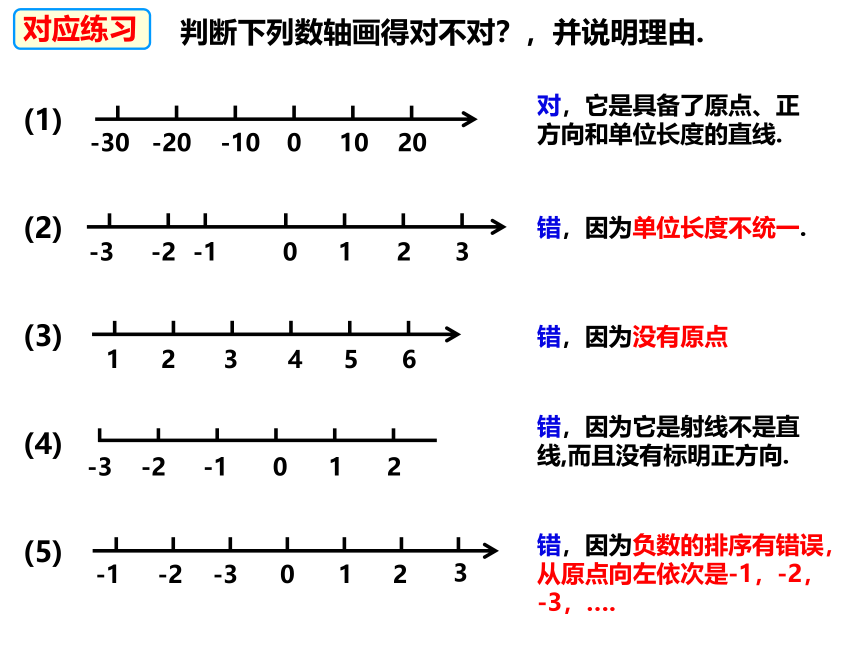
判断下列数轴画得对不对?,并说明理由.
对应练习
10
20
0
-10
-20
-30
(1)
对,它是具备了原点、正方向和单位长度的直线.
(2)
1
2
3
0
-1
-2
-3
错,因为单位长度不统一.
(3)
5
6
4
3
2
1
错,因为没有原点
(4)
1
2
0
-1
-2
-3
错,因为它是射线不是直线,而且没有标明正方向.
1
2
0
-3
-2
-1
(5)
3
错,因为负数的排序有错误,从原点向左依次是-1,-2,-3,….
例 1 说出下图所示的数轴上 A,B,C,D 各表示的数.
1
2
0
-1
-2
-3
-3.5
D
C
A
B
解:点A在原点左边与原点距离2个单位长度,故表示-2.
点B在原点左边与原点距离3.5个单位长度,故表示-3.5.
点D在原点右边与原点距离2个单位长度,故表示2.
点C在原点表示0.
题型一:根据数轴上的点读出有理数
例 1 说出下图所示的数轴上 A,B,C,D 各表示的数.
1
2
0
-1
-2
-3
-3.5
D
C
A
B
思考:如何确定数轴上的点所表示的数?
从两方面考虑:
(1) 点的位置:原点表示0,原点右边的点表示正数,原点左边的点表示负数;
(2) 确定该点到原点的距离.
题型一:根据数轴上的点读出有理数
例 2 在数轴上,画出表示下列各数的点:
注意:① 把点标在线上; ② 把数标在点的上方.
3
4
2
0
-1
+4,- , ,-1.25,-4
1
2
1
2
1
-2
-3
-4
解:+4用数轴上位于原点右边与原点距离4个单位长度的点表示.
+4
- 用数轴上位于原点左边与原点距离 个单位长度的点表示.
1
2
1
2
1
2
-
1
2
-1.25
-4
用数轴上位于原点左边与原点距离 个单位长度的点表示.
1
2
1
2
题型二:用数轴上的点表示给定的有理数
例 2 在数轴上,画出表示下列各数的点:
3
4
2
0
-1
+4,- , ,-1.25,-4
1
2
1
2
1
-2
-3
-4
+4
1
2
-
1
2
-1.25
-4
题型二:用数轴上的点表示给定的有理数
归纳总结:
一般地,任意一个有理数,都可以用数轴上的一个点来表示,
但反过来就不成立了,即数轴上的点表示的不一定都是有理数,
如π能在数轴上表示,但不是有理数.
-2500
0
-1000
500
-2000
-500
-1500
分别画出数轴,并在数轴上表示下列各数
-5
-4
-3
-2
-1
0
2
1
3
解:(1)
+2.5
-3
1.5
-0.5
0
-2500
-2000
500
-1000
对应练习
(1) - +2.5 -3 1.5 0 -0.5
(2) -1000 500 -2000 -2500
(2)
注意: 原点的选定、正方向的选取、单位长度大小的确定,都是根据实际需要“选定”的.
5
4
5
4
-
1、下列语句:
① 数轴上的点只能表示整数;
② 数轴是一条线段;
③ 数轴上的点只能表示一个数;
④ 数轴上找不到既不表示正数,又不表示负数的点;
⑤ 数轴上的点所表示的数都是有理数.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
巩固练习
A
2、一个点从数轴上的原点出发,向右走3个单位长度,再向左移动5个单位长度,到达终点所表示的数是( )
巩固练习
A.8 B.-8 C.2 D.-2
方法点拨:数轴的引入,使我们能用直观图形来解数的有关概念,这就是“数”与“形”的结合,数形结合是一种重要的方法,我们应注意掌握。
D
① 3和-3在原点 ,3在原点 ,-3在原点 ,到原点距离都是 .
② 一般地,设a是一个正数,则数轴上表示数a在原点的 边,与原点的距离是 个单位长度;表示数-a的点在原点的 边,与原点的距离是 个单位长度.
3、观察数轴上的有理数与原点的关系
右
a
左
a
3
4
2
0
-1
1
-2
-3
-4
两边
右边
左边
3个单位长度
③ 数轴上,与原点距离为 4 的单位长度的点有 个,它们表示的数分别为 .
2
+4 或 -4
±4
巩固练习
4、数轴上有一点A,一只蚂蚁从A出发爬了8个单位长度到了原点,则点A所表示的数是________.
±8
5、在数轴上到表示 -2 的点相距 8 个单位长度的点表示的数为 .
巩固练习
-10或6
6、在数轴上,表示-1和3的两点间的距离是 .
7、若在数轴上表示数-1和2019的两点分别为点A和点B,则A,B两点之间的距离为( )
A.2018 B.2019 C.2020 D.2021
巩固练习
4
C
8、如果数轴上点A到原点的距离为5,点B到原点的距离为9,那么A,B两点的距离是 .
8或14
9、如图,数轴上一点A向左移动2个单位长度到达点B,再向右移动5个单位长度到达点C.若点C表示的数为1,则点A表示的数( )
巩固练习
A.7 B.3 C.-3 D.-2
D
10、在数轴上点A表示-4,如果把原点0向负方向移动1.5个单位,那么在新数轴上点A表示的数是( )
C
A. -5 B.-4 C. -2.5 D.2
1
2
1
2
巩固练习
数轴上的两个点,右边点表示的数与左边点表示的数的大小关系?
数轴上不同的两个点表示的数,右边点表示的数总比左边点表示的数大.
0大于负数,
正数大于负数。
正数大于0,
越来越大
3
2
0
-1
1
-2
-3
即
负数<0<正数
探究思考
拓展提升
操作探究:已知在纸面上有一数轴(如图所示).
左右折叠纸面,折痕所在的直线与数轴的交点为“对折中心点”
操作一:
(1) 左右折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与 表示的点重合;
操作二:
(2) 左右折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①对折中心点所表示的数为 .对折后5表示的点与数 表示的点重合;
②若数轴上A、B两点之间距离为11(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
3
1
-3
A、B两点表示的数分别是-4.5,6.5.
本节课你有什么收获?
数轴
画法
定义
规定了原点、正方向和单位长度的直线叫做数轴.
一画:画一条直线 (一般画成水平的直线);
二取:在这条直线的适当位置取一点作
为原点,用0表示;
三定:确定正方向,并用箭头表示.
四选:根据需要选取适当单位长度,
并标上数字.
应用
根据数轴上的点读出有理数
用数轴上的点表示给定的有理数
数形结合解决问题
1.2.1 数轴
注意:有理数可以按整数和分数来分类;
也可以按照正有理数、负有理数 和 0 来分类,
一、有理数的概念
二、有理数的分类:
整数和分数统称有理数.
方法点拨:① 有限小数、无限循环小数、百分数都可以化为分数,因此这些数都是有理数.
② 到现在为止,我们学过的数(π 和无限不循环小数除外)都是有理数.
有理数
整数
分数
正整数
0
负整数
正分数
负分数
有理数
正有理数
负有理数
0
正整数
正分数
负整数
负分数
有理数的分类必须做到不重不漏,千万不要忘记 0,0是整数,但0既不是正数,也不是负数.
但是要注意一点:
B
A
C
(3) 温度计刻度的正负是怎样规定的?以什么为基准?基准刻度线表示多少摄氏度?
情境引入
问题一:观察如图的温度计,回答下列问题:
(1) 点A表示多少摄氏度?点B呢?点C呢?
在0℃以上为正,0℃以下为负,温度计是以0℃为基准的.
(4) 每摄氏度两条刻度线之间的距离有什么特点
距离相等
(2) A,B,C三点所表示的温度哪个高?哪个低?
0℃
20℃
-5℃
A点所表示的温度最高,B点所表示的温度最低.
情境引入
问题二:让机器人在一条东西向的直路上做走步取物试验.根据指令:它由O处出发,向西走3m到达A点处,拿取物品,然后,返回点O处将物品放入蓝中,在向东走2m到达点B处取物.
1、在课本P7图1-3所示的直线上画出A、B两处的位置。
2、把向东走记作“+”,向西走记作“-”,在上面的直线上标出与A、B相对应的数.
A
B
-3
+2
探究新知
思考:根据前面的两个问题,你能用一条直线上的点表示有理数吗?
在直线上从原点向右,每隔一个单位长度取一点,这些点依次表示1,2,3,4
,......,
(当直线水平放置时,一般取从左到右的方向为正方向,并用箭头表示),
探究新知
下面,我们来学习用直线上的点来表示数.
第一步:画一条直线,在这条直线上任取一点,叫做原点,
0
第二步:规定这条直线的一个方向为正方向
相反
第三步:适当地选取某一长度作为单位长度,
从原点向左,每隔一个单位长度取一点,他们依次表示 -1,-2,-3,-4,...... ;
用这点表示数0.
的方向就是负方向。
1
2
3
4
-1
-2
-3
-4
同一数轴上的单位长度必须相同.
概念学习
0
1
2
3
4
-1
-2
-3
-4
像这样规定了原点、正方向和单位长度的直线叫做数轴.
数轴定义包含三层含义:
① 数轴是一条直线,它可以向两端无限延伸
正方向
② 数轴的三要素
原点
单位长度
三者缺一不可
③ 原点的选定、正方向的选取、单位长度大小的确定,都是根据实际需要“选定”的.
概念学习
0
1
2
3
4
-1
-2
-3
-4
像这样规定了原点、正方向和单位长度的直线叫做数轴.
画数轴的步骤:
一画:画一条直线 (一般画成水平的直线);
二取:在这条直线的适当位置取一点作为原点,用0表示;
三定:确定正方向,并用箭头表示.
四选:根据需要选取适当单位长度,并标上数字.
判断下列数轴画得对不对?,并说明理由.
对应练习
10
20
0
-10
-20
-30
(1)
对,它是具备了原点、正方向和单位长度的直线.
(2)
1
2
3
0
-1
-2
-3
错,因为单位长度不统一.
(3)
5
6
4
3
2
1
错,因为没有原点
(4)
1
2
0
-1
-2
-3
错,因为它是射线不是直线,而且没有标明正方向.
1
2
0
-3
-2
-1
(5)
3
错,因为负数的排序有错误,从原点向左依次是-1,-2,-3,….
例 1 说出下图所示的数轴上 A,B,C,D 各表示的数.
1
2
0
-1
-2
-3
-3.5
D
C
A
B
解:点A在原点左边与原点距离2个单位长度,故表示-2.
点B在原点左边与原点距离3.5个单位长度,故表示-3.5.
点D在原点右边与原点距离2个单位长度,故表示2.
点C在原点表示0.
题型一:根据数轴上的点读出有理数
例 1 说出下图所示的数轴上 A,B,C,D 各表示的数.
1
2
0
-1
-2
-3
-3.5
D
C
A
B
思考:如何确定数轴上的点所表示的数?
从两方面考虑:
(1) 点的位置:原点表示0,原点右边的点表示正数,原点左边的点表示负数;
(2) 确定该点到原点的距离.
题型一:根据数轴上的点读出有理数
例 2 在数轴上,画出表示下列各数的点:
注意:① 把点标在线上; ② 把数标在点的上方.
3
4
2
0
-1
+4,- , ,-1.25,-4
1
2
1
2
1
-2
-3
-4
解:+4用数轴上位于原点右边与原点距离4个单位长度的点表示.
+4
- 用数轴上位于原点左边与原点距离 个单位长度的点表示.
1
2
1
2
1
2
-
1
2
-1.25
-4
用数轴上位于原点左边与原点距离 个单位长度的点表示.
1
2
1
2
题型二:用数轴上的点表示给定的有理数
例 2 在数轴上,画出表示下列各数的点:
3
4
2
0
-1
+4,- , ,-1.25,-4
1
2
1
2
1
-2
-3
-4
+4
1
2
-
1
2
-1.25
-4
题型二:用数轴上的点表示给定的有理数
归纳总结:
一般地,任意一个有理数,都可以用数轴上的一个点来表示,
但反过来就不成立了,即数轴上的点表示的不一定都是有理数,
如π能在数轴上表示,但不是有理数.
-2500
0
-1000
500
-2000
-500
-1500
分别画出数轴,并在数轴上表示下列各数
-5
-4
-3
-2
-1
0
2
1
3
解:(1)
+2.5
-3
1.5
-0.5
0
-2500
-2000
500
-1000
对应练习
(1) - +2.5 -3 1.5 0 -0.5
(2) -1000 500 -2000 -2500
(2)
注意: 原点的选定、正方向的选取、单位长度大小的确定,都是根据实际需要“选定”的.
5
4
5
4
-
1、下列语句:
① 数轴上的点只能表示整数;
② 数轴是一条线段;
③ 数轴上的点只能表示一个数;
④ 数轴上找不到既不表示正数,又不表示负数的点;
⑤ 数轴上的点所表示的数都是有理数.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
巩固练习
A
2、一个点从数轴上的原点出发,向右走3个单位长度,再向左移动5个单位长度,到达终点所表示的数是( )
巩固练习
A.8 B.-8 C.2 D.-2
方法点拨:数轴的引入,使我们能用直观图形来解数的有关概念,这就是“数”与“形”的结合,数形结合是一种重要的方法,我们应注意掌握。
D
① 3和-3在原点 ,3在原点 ,-3在原点 ,到原点距离都是 .
② 一般地,设a是一个正数,则数轴上表示数a在原点的 边,与原点的距离是 个单位长度;表示数-a的点在原点的 边,与原点的距离是 个单位长度.
3、观察数轴上的有理数与原点的关系
右
a
左
a
3
4
2
0
-1
1
-2
-3
-4
两边
右边
左边
3个单位长度
③ 数轴上,与原点距离为 4 的单位长度的点有 个,它们表示的数分别为 .
2
+4 或 -4
±4
巩固练习
4、数轴上有一点A,一只蚂蚁从A出发爬了8个单位长度到了原点,则点A所表示的数是________.
±8
5、在数轴上到表示 -2 的点相距 8 个单位长度的点表示的数为 .
巩固练习
-10或6
6、在数轴上,表示-1和3的两点间的距离是 .
7、若在数轴上表示数-1和2019的两点分别为点A和点B,则A,B两点之间的距离为( )
A.2018 B.2019 C.2020 D.2021
巩固练习
4
C
8、如果数轴上点A到原点的距离为5,点B到原点的距离为9,那么A,B两点的距离是 .
8或14
9、如图,数轴上一点A向左移动2个单位长度到达点B,再向右移动5个单位长度到达点C.若点C表示的数为1,则点A表示的数( )
巩固练习
A.7 B.3 C.-3 D.-2
D
10、在数轴上点A表示-4,如果把原点0向负方向移动1.5个单位,那么在新数轴上点A表示的数是( )
C
A. -5 B.-4 C. -2.5 D.2
1
2
1
2
巩固练习
数轴上的两个点,右边点表示的数与左边点表示的数的大小关系?
数轴上不同的两个点表示的数,右边点表示的数总比左边点表示的数大.
0大于负数,
正数大于负数。
正数大于0,
越来越大
3
2
0
-1
1
-2
-3
即
负数<0<正数
探究思考
拓展提升
操作探究:已知在纸面上有一数轴(如图所示).
左右折叠纸面,折痕所在的直线与数轴的交点为“对折中心点”
操作一:
(1) 左右折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与 表示的点重合;
操作二:
(2) 左右折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①对折中心点所表示的数为 .对折后5表示的点与数 表示的点重合;
②若数轴上A、B两点之间距离为11(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
3
1
-3
A、B两点表示的数分别是-4.5,6.5.
本节课你有什么收获?
数轴
画法
定义
规定了原点、正方向和单位长度的直线叫做数轴.
一画:画一条直线 (一般画成水平的直线);
二取:在这条直线的适当位置取一点作
为原点,用0表示;
三定:确定正方向,并用箭头表示.
四选:根据需要选取适当单位长度,
并标上数字.
应用
根据数轴上的点读出有理数
用数轴上的点表示给定的有理数
数形结合解决问题
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
