人教版八年级数学上学期 12.2.3全等三角形的判定(第三课时ASA,AAS) 课件(共22张PPT)
文档属性
| 名称 | 人教版八年级数学上学期 12.2.3全等三角形的判定(第三课时ASA,AAS) 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 16:55:22 | ||
图片预览






文档简介
(共22张PPT)
第12.2.3全等三角形的判定
(第三课时ASA、AAS)
人教版数学八年级上册
学习目标
1.掌握三角形全等“ASA”和“AAS”的条件.
2.能运用“ASA”和“AAS”条件判定两个三角形全等.
3、通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
情境引入
三条边分别相等的三角形全等(SSS).
上节课我们学习了什么方法可以判定两个三角形全等?
除了上面的方法,还有其他方法能判定两个三角形全等吗?我们继续探索三角形全等的条件.
两边和它们的夹角分别相等的两个三角形全等(SAS).
(2) 三条边
(1) 三个角
(3) 两边一角
(4) 两角一边
SSS
不能
当两个三角形满足六个条件中的三个条件时,有四种情况:
情境引入
两边和它们的夹角分别相等的两个三角形全等
两边和其中一边的对角对应相等的两个三角形不一定全等
互动新授
这节课我们一起来探究满足两边一角时,能否判定两个三角形全等呢?
(2)两角及一角的对边
(1)两角及其夹边
互动新授
先任意画出一个△ABC,再画一个△A′B′C′,使得AB=A′B′,∠A=∠A′,∠B=∠B′(即两角和它们的夹边分别相等).此时的△ABC和△A′B′C′全等吗?
画法:1、画A′B′=AB.
2、在A′B′的同旁画∠DA′B′=∠A,∠EB′A′=∠B,A′D,B′E相交于点C′.
3、△A′B′C′即为所作三角形.
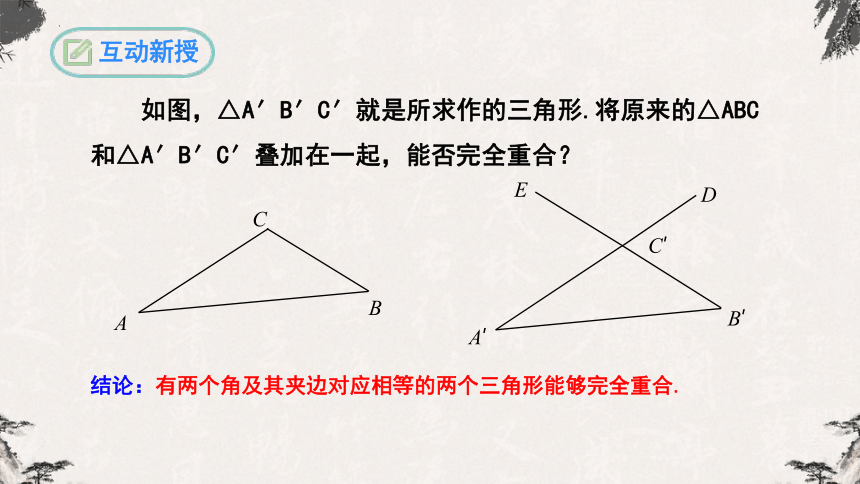
结论:有两个角及其夹边对应相等的两个三角形能够完全重合.
C
A
B
C′
A′
B′
E
D
如图,△A′B′C′就是所求作的三角形.将原来的△ABC和△A′B′C′叠加在一起,能否完全重合?
互动新授
互动新授
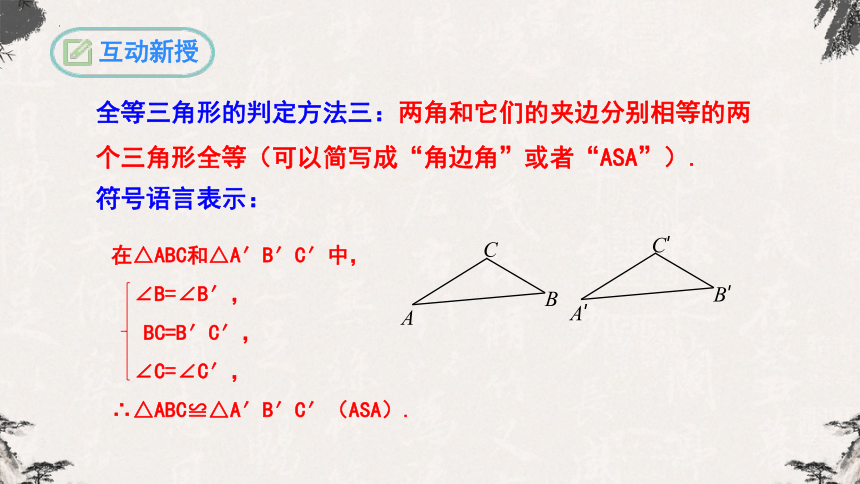
全等三角形的判定方法三:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”).
符号语言表示:
C
A
B
C′
A′
B′
在△ABC和△A′B′C′中,
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(ASA).
典例精析
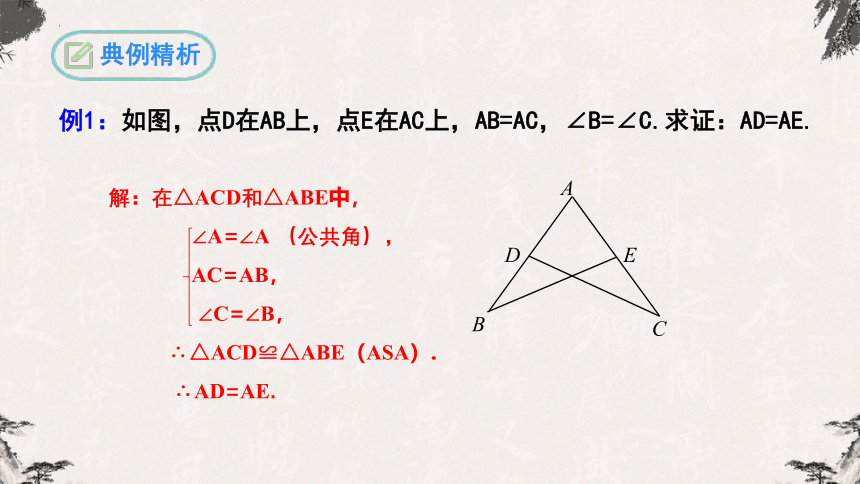
例1:如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
解:在△ACD和△ABE中,
∠A=∠A (公共角),
AC=AB,
∠C=∠B,
∴△ACD≌△ABE(ASA).
∴AD=AE.
D
E
B
C
A
典例精析
例2:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.
A
B
E
D
C
F
分析:BC,EF不是已知两对角的夹边,
在三角形中,知道两个角的关系,利用三角形内角和定理可以求得∠C和∠F之间的关系呢?
最后,通过转化来构造“ASA”的判定条件来证明
典例精析
例2:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.
A
B
E
D
C
F
证明:在△ABC和△DEF中,
∵∠A=∠D,∠B=∠E,
∴∠C=180°-∠A-∠B,∠F=180°-∠D-∠E,
即∠C=∠F.
在△ABC和△DEF中,
∠B=∠E,
BC=EF,
∠C=∠F,
∴△ABC≌△DEF(ASA).
通过例题2,你可以得到什么结论呢?两角和其中一角的对边对应相等的
两个三角形会全等吗?
A
B
E
D
C
F
总结归纳
全等三角形的判定方法四:两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或者“AAS”).
符号语言表示:
证明:在△ABC和△DEF中,
∠A=∠D,
∠B=∠E,
BC=EF,
∴△ABC≌△DEF(AAS).
如图,已知∠1=∠2,∠C=∠D.求证:AC=AD.
证明:∵∠1=∠2,∠C=∠D,
∴∠ABC=∠ABD
在△ABC和△ABD中,
∠1=∠2,
AB=AB(公共边),
∠ABC=∠ABD,
∴△ABC≌△ABD(ASA).
∴AC=AD.
A
B
1
2
C
D
小试牛刀
1.已知,如图AB⊥BC,AD⊥DC,垂足分别为B,D,∠1=∠2.求证:AB=AD
证明:∵AB⊥BC, AD⊥DC
∴∠B=∠D= 90°
在ΔABC与ΔADC中
∠B= ∠D
∠1= ∠2
AC=AC
∴ΔABC≌ΔADC(AAS)
∴AB=AD
课堂检测
2.已知,如图,点E是AC上一点,AB=CE,AB//CD,∠ACB=∠D.求证:BC=ED.
证明:∵AB//CD,
∴∠A=∠ECD.
在△ACB和△CDE中,
∠ACB=∠D,
∠A=∠ECD,
AB=CE,
∴△ACB≌△CDE(AAS).
∴BC=ED.
A
B
E
C
D
课堂检测
1.如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D,使BC=CD,再作出BF的垂线DE,使A,C,E三点在一条直线上,这时测得DE的长就是A、B两点间的距离,为什么?
证明:∵AB⊥BF, DE⊥BF
∴∠ABC=∠EDC= 90°
在ΔABC与ΔEDC中
∠ABC= ∠EDC
∠1= ∠2
BC=DC
2
1
∴ΔABC≌ΔEDC(ASA)
∴AB=ED
拓展训练
2.如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:BO=CO.
证明:在△ACD和△ABE中,
A
B
C
D
E
O
∴△ACD≌△ABE(ASA),
∴AD=AE.
拓展训练
∵AB=AC,
∴AB-AD=AC-AE.
即BD=CE.
在△BOD和△COE中,
∴△BOD≌△COE(AAS).
∴BO=CO.
A
B
C
D
E
O
拓展训练
课堂小结
1.三角形全等的判定:ASA和AAS
2.利用ASA和AAS解决实际问题
3.截止现在我们学习了几种三角形全等的判定方法?
(1)全等三角形的定义;
(2)边边边(SSS);
(3)边角边(SAS);
(4)角边角(ASA);
(5)角角边(AAS).
1.如图,已知:AD为△ABC的中线,且CF⊥AD于点F,BE⊥AD交AD的延长线于点E.求证:BE=CF.
证明:∵AD为△ABC的中线,
∴BD=CD.
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°.
在△BED与△CFD中,
∴△BED≌△CFD(AAS).
∴BE=CF.
课后作业
2.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:△BEC≌△CDA.
证明:∵∠ACB=90°,BE⊥CE,AD⊥CE,
∴∠BEC=∠ADC=90°,
∴∠BCE+∠CBE=90°,
∠BCE+∠ACD=90°,
∴∠CBE=∠ACD,
∵AC=BC,
∴△BEC≌△CDA(AAS)
课后作业
谢谢聆听
第12.2.3全等三角形的判定
(第三课时ASA、AAS)
人教版数学八年级上册
学习目标
1.掌握三角形全等“ASA”和“AAS”的条件.
2.能运用“ASA”和“AAS”条件判定两个三角形全等.
3、通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
情境引入
三条边分别相等的三角形全等(SSS).
上节课我们学习了什么方法可以判定两个三角形全等?
除了上面的方法,还有其他方法能判定两个三角形全等吗?我们继续探索三角形全等的条件.
两边和它们的夹角分别相等的两个三角形全等(SAS).
(2) 三条边
(1) 三个角
(3) 两边一角
(4) 两角一边
SSS
不能
当两个三角形满足六个条件中的三个条件时,有四种情况:
情境引入
两边和它们的夹角分别相等的两个三角形全等
两边和其中一边的对角对应相等的两个三角形不一定全等
互动新授
这节课我们一起来探究满足两边一角时,能否判定两个三角形全等呢?
(2)两角及一角的对边
(1)两角及其夹边
互动新授
先任意画出一个△ABC,再画一个△A′B′C′,使得AB=A′B′,∠A=∠A′,∠B=∠B′(即两角和它们的夹边分别相等).此时的△ABC和△A′B′C′全等吗?
画法:1、画A′B′=AB.
2、在A′B′的同旁画∠DA′B′=∠A,∠EB′A′=∠B,A′D,B′E相交于点C′.
3、△A′B′C′即为所作三角形.
结论:有两个角及其夹边对应相等的两个三角形能够完全重合.
C
A
B
C′
A′
B′
E
D
如图,△A′B′C′就是所求作的三角形.将原来的△ABC和△A′B′C′叠加在一起,能否完全重合?
互动新授
互动新授
全等三角形的判定方法三:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”).
符号语言表示:
C
A
B
C′
A′
B′
在△ABC和△A′B′C′中,
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(ASA).
典例精析
例1:如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
解:在△ACD和△ABE中,
∠A=∠A (公共角),
AC=AB,
∠C=∠B,
∴△ACD≌△ABE(ASA).
∴AD=AE.
D
E
B
C
A
典例精析
例2:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.
A
B
E
D
C
F
分析:BC,EF不是已知两对角的夹边,
在三角形中,知道两个角的关系,利用三角形内角和定理可以求得∠C和∠F之间的关系呢?
最后,通过转化来构造“ASA”的判定条件来证明
典例精析
例2:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.
A
B
E
D
C
F
证明:在△ABC和△DEF中,
∵∠A=∠D,∠B=∠E,
∴∠C=180°-∠A-∠B,∠F=180°-∠D-∠E,
即∠C=∠F.
在△ABC和△DEF中,
∠B=∠E,
BC=EF,
∠C=∠F,
∴△ABC≌△DEF(ASA).
通过例题2,你可以得到什么结论呢?两角和其中一角的对边对应相等的
两个三角形会全等吗?
A
B
E
D
C
F
总结归纳
全等三角形的判定方法四:两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或者“AAS”).
符号语言表示:
证明:在△ABC和△DEF中,
∠A=∠D,
∠B=∠E,
BC=EF,
∴△ABC≌△DEF(AAS).
如图,已知∠1=∠2,∠C=∠D.求证:AC=AD.
证明:∵∠1=∠2,∠C=∠D,
∴∠ABC=∠ABD
在△ABC和△ABD中,
∠1=∠2,
AB=AB(公共边),
∠ABC=∠ABD,
∴△ABC≌△ABD(ASA).
∴AC=AD.
A
B
1
2
C
D
小试牛刀
1.已知,如图AB⊥BC,AD⊥DC,垂足分别为B,D,∠1=∠2.求证:AB=AD
证明:∵AB⊥BC, AD⊥DC
∴∠B=∠D= 90°
在ΔABC与ΔADC中
∠B= ∠D
∠1= ∠2
AC=AC
∴ΔABC≌ΔADC(AAS)
∴AB=AD
课堂检测
2.已知,如图,点E是AC上一点,AB=CE,AB//CD,∠ACB=∠D.求证:BC=ED.
证明:∵AB//CD,
∴∠A=∠ECD.
在△ACB和△CDE中,
∠ACB=∠D,
∠A=∠ECD,
AB=CE,
∴△ACB≌△CDE(AAS).
∴BC=ED.
A
B
E
C
D
课堂检测
1.如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D,使BC=CD,再作出BF的垂线DE,使A,C,E三点在一条直线上,这时测得DE的长就是A、B两点间的距离,为什么?
证明:∵AB⊥BF, DE⊥BF
∴∠ABC=∠EDC= 90°
在ΔABC与ΔEDC中
∠ABC= ∠EDC
∠1= ∠2
BC=DC
2
1
∴ΔABC≌ΔEDC(ASA)
∴AB=ED
拓展训练
2.如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:BO=CO.
证明:在△ACD和△ABE中,
A
B
C
D
E
O
∴△ACD≌△ABE(ASA),
∴AD=AE.
拓展训练
∵AB=AC,
∴AB-AD=AC-AE.
即BD=CE.
在△BOD和△COE中,
∴△BOD≌△COE(AAS).
∴BO=CO.
A
B
C
D
E
O
拓展训练
课堂小结
1.三角形全等的判定:ASA和AAS
2.利用ASA和AAS解决实际问题
3.截止现在我们学习了几种三角形全等的判定方法?
(1)全等三角形的定义;
(2)边边边(SSS);
(3)边角边(SAS);
(4)角边角(ASA);
(5)角角边(AAS).
1.如图,已知:AD为△ABC的中线,且CF⊥AD于点F,BE⊥AD交AD的延长线于点E.求证:BE=CF.
证明:∵AD为△ABC的中线,
∴BD=CD.
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°.
在△BED与△CFD中,
∴△BED≌△CFD(AAS).
∴BE=CF.
课后作业
2.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:△BEC≌△CDA.
证明:∵∠ACB=90°,BE⊥CE,AD⊥CE,
∴∠BEC=∠ADC=90°,
∴∠BCE+∠CBE=90°,
∠BCE+∠ACD=90°,
∴∠CBE=∠ACD,
∵AC=BC,
∴△BEC≌△CDA(AAS)
课后作业
谢谢聆听
