2021-2022学年人教版数学八年级上册13.3.2等边三角形 课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册13.3.2等边三角形 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
等边三角形
1、掌握等边三角形的定义;
2、探索等边三角形的性质和判定
方法;(重点)
3、能熟练地运用等边三角形的性
质和判定解决问题。(难点)
学习目标
新课导入
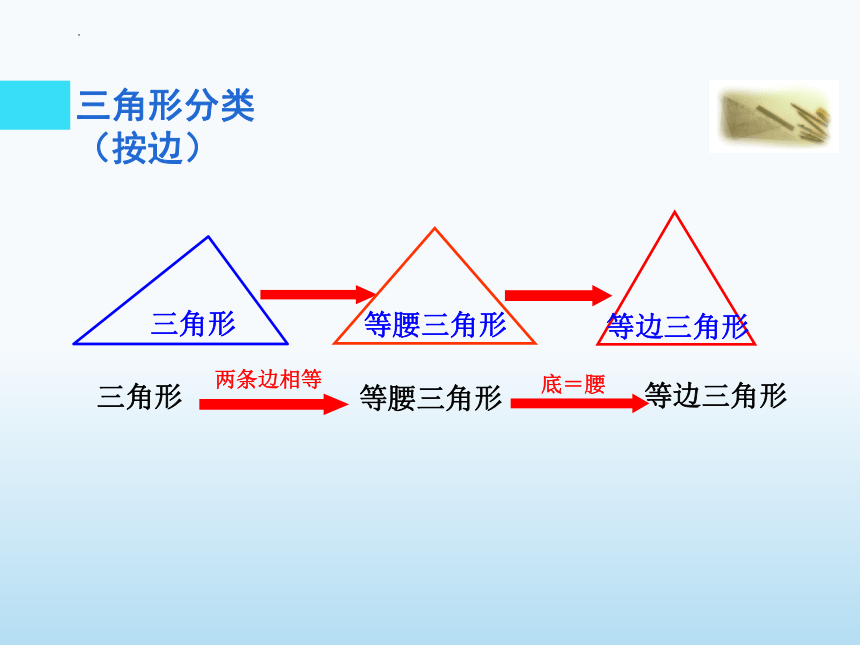
三角形
三角形
两条边相等
等腰三角形
等腰三角形
底=腰
等边三角形
等边三角形
三角形分类(按边)
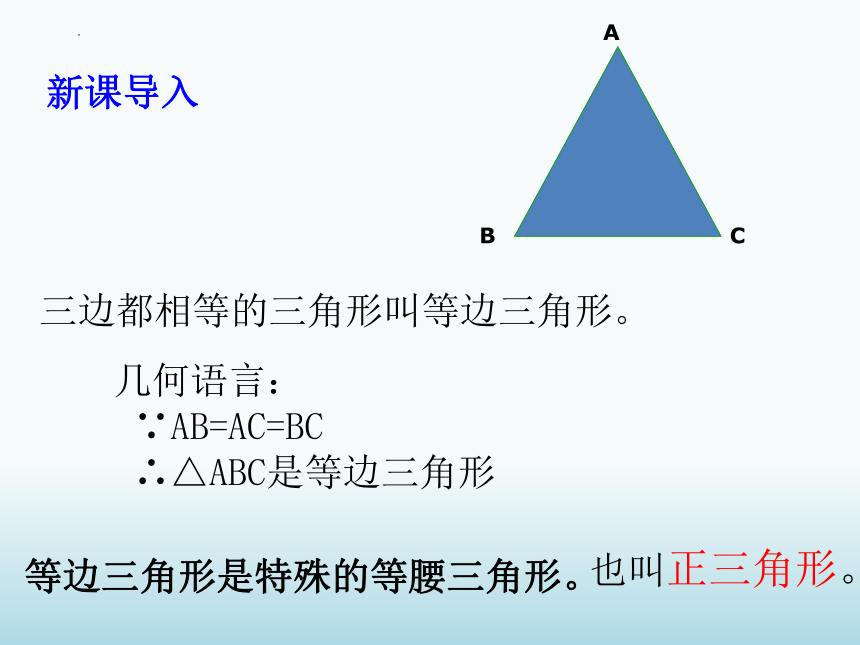
等边三角形是特殊的等腰三角形。
A
B
C
几何语言:
∵AB=AC=BC
∴△ABC是等边三角形
三边都相等的三角形叫等边三角形。
也叫正三角形。
新课导入
图形 等腰三角形
性 质
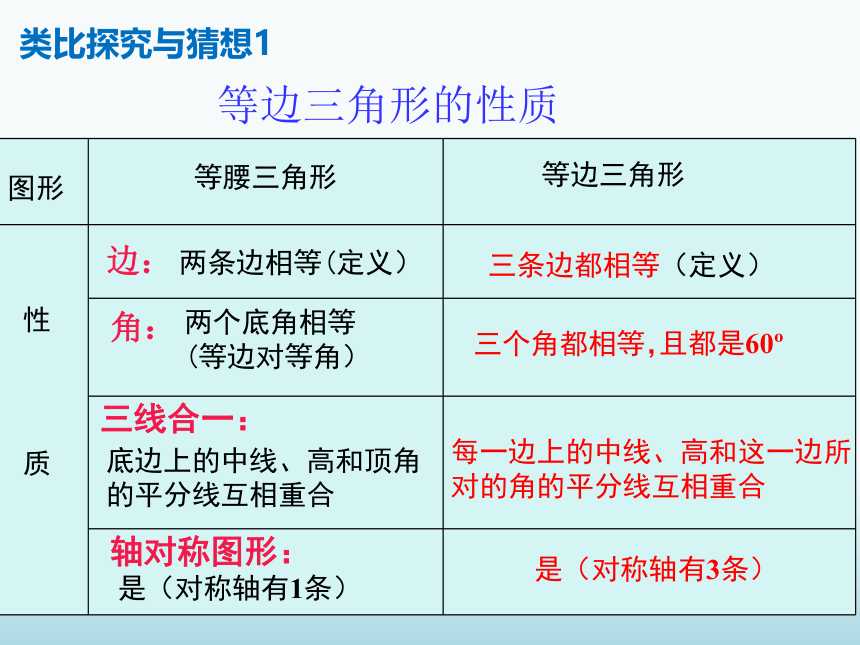
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
是(对称轴有3条)
等边三角形
是(对称轴有1条)
两个底角相等
(等边对等角)
底边上的中线、高和顶角
的平分线互相重合
且都是60
两条边相等(定义)
三条边都相等(定义)
边:
角:
类比探究与猜想1
等边三角形的性质
三线合一:
轴对称图形:
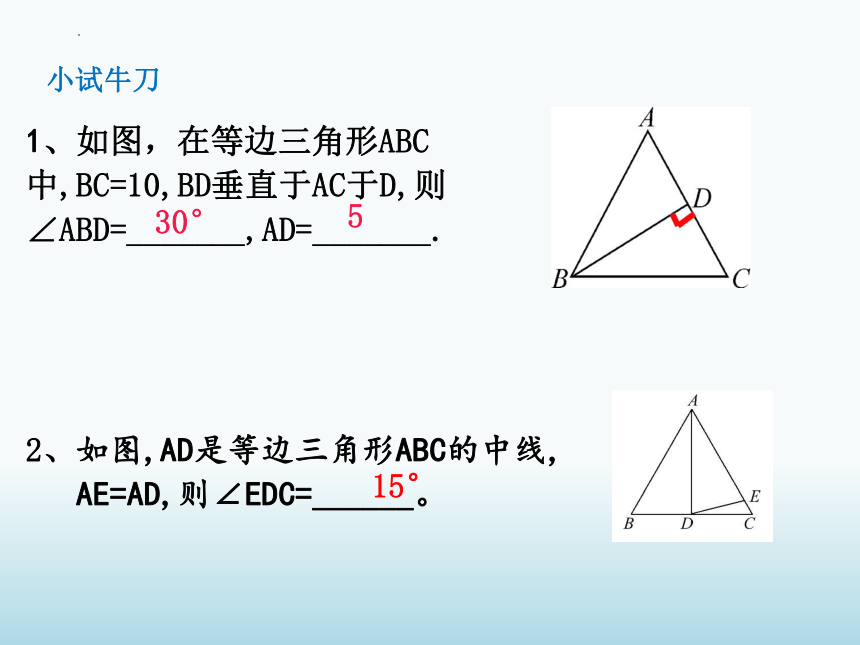
1、如图,在等边三角形ABC中,BC=10,BD垂直于AC于D,则∠ABD=_______,AD=_______.
2、如图,AD是等边三角形ABC的中线,
AE=AD,则∠EDC=______。
15°
小试牛刀
30°
5
一个三角形满足什么条件就是等边三角形
探究:等边三角形的判定
图形 等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形(定义)
三条边都相等的三角形是等边三角形(定义)
类比探究与猜想2
已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证: ⊿ ABC是等边三角形。
A
B
C
证明:
在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=AC(等角对等边)
同理 ,∵∠B=∠C
∴ AC=AB
∴AB=AC=BC
即⊿ ABC是等边三角形。
A
B
C
∵ ∠A= ∠ B= ∠ C
∴△ABC是等边三角形
三个角都相等的三角形是等边三角形。
三个角相等可以证明是等边三角形。
那么两个角可以吗?
两个60°的角可以吗?
一个60°的角可以吗?
如果一个等腰三角形中有一个角是60°,那么这个三角形是等边三角形?
第一种情况:当顶角是60度时
第二种情况:当底角是60度时
(不可以)
(可以)
(不可以)
已知: ⊿ABC中,AB=AC, ∠ A=600。
求证: ⊿ ABC是等边三角形。
A
B
C
证明:∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴∠B+∠C=120°
∴ ∠B=∠C = 600
∴∠A=∠B=∠C
∴ ⊿ ABC是等边三角形
讨论:如果∠ B=600 或是 ∠ C=600 ,
它是等边三角形吗?
有一个角是 60°的等腰三角形是等边三角形。
A
B
C
几何语言:
∵ ∠B=600 AB=BC
∴△ABC是等边三角形
2. 三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角
形是等边三角形.
1.三边都相等的三角形是等边三角形.(定义)
一般三角形
等边三角形
A
B
C
等腰三角形
等边三角形
A
B
C
∵AB=BC=AC
∴△ABC是等边三角形
∵ ∠B=600 AB=BC
∴△ABC是等边三角形
∵ ∠A= ∠ B= ∠ C
∴△ABC是等边三角形
等边三角形的判定方法
辩一辩:根据条件判断下列三角形是否为等边三角形.
(1)
(2)
(6)
(5)
不
是
是
是
是
是
(4)
(3)
不一定
是
练习 如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C,
∴ ∠A= ∠ADE= ∠ AED,
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
证明:∵ △ABC 是等边三角形,
∴ ∠A =∠ABC =∠ACB =60°.
∵ DE∥BC,
∴ ∠ABC =∠ADE,
∠ACB =∠AED,
∴ ∠A =∠ADE =∠AED,
∴ △ADE 是等边三角形.
【变式1】若点D、E 在边AB、AC 的延长线上,且 DE∥BC,结论还成立吗?
A
D
E
B
C
【变式2】若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E,
∴ ∠EAD =∠D =∠E,
∴ △ADE 是等边三角形.
A
D
E
B
C
【变式3】上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A==60°,
∵ AD=AE,
∴ △ADE是等腰三角形,
∴ △ADE是等边三角形.
同学们,这节课你有什么收获呢?
等边
三角形
定义
底=腰
性质
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
三边法
三角法
等腰三角形法
课堂总结
如图,等边三角形ABC中,AD是BC上的高,∠BDE= ∠CDF=60°,结合图形,图中有哪些与BD相等的线段?
相等的角?
等腰三角形?
等边三角形?
其他?
A
C
B
D
E
F
课下思考:
严格性之于数学家,犹如道德之于人。
证明的规范性在于:条理清晰,因果相应,言必有据。
这是初学证明者谨记和遵循的原则。
寄语
等边三角形
1、掌握等边三角形的定义;
2、探索等边三角形的性质和判定
方法;(重点)
3、能熟练地运用等边三角形的性
质和判定解决问题。(难点)
学习目标
新课导入
三角形
三角形
两条边相等
等腰三角形
等腰三角形
底=腰
等边三角形
等边三角形
三角形分类(按边)
等边三角形是特殊的等腰三角形。
A
B
C
几何语言:
∵AB=AC=BC
∴△ABC是等边三角形
三边都相等的三角形叫等边三角形。
也叫正三角形。
新课导入
图形 等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
是(对称轴有3条)
等边三角形
是(对称轴有1条)
两个底角相等
(等边对等角)
底边上的中线、高和顶角
的平分线互相重合
且都是60
两条边相等(定义)
三条边都相等(定义)
边:
角:
类比探究与猜想1
等边三角形的性质
三线合一:
轴对称图形:
1、如图,在等边三角形ABC中,BC=10,BD垂直于AC于D,则∠ABD=_______,AD=_______.
2、如图,AD是等边三角形ABC的中线,
AE=AD,则∠EDC=______。
15°
小试牛刀
30°
5
一个三角形满足什么条件就是等边三角形
探究:等边三角形的判定
图形 等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形(定义)
三条边都相等的三角形是等边三角形(定义)
类比探究与猜想2
已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证: ⊿ ABC是等边三角形。
A
B
C
证明:
在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=AC(等角对等边)
同理 ,∵∠B=∠C
∴ AC=AB
∴AB=AC=BC
即⊿ ABC是等边三角形。
A
B
C
∵ ∠A= ∠ B= ∠ C
∴△ABC是等边三角形
三个角都相等的三角形是等边三角形。
三个角相等可以证明是等边三角形。
那么两个角可以吗?
两个60°的角可以吗?
一个60°的角可以吗?
如果一个等腰三角形中有一个角是60°,那么这个三角形是等边三角形?
第一种情况:当顶角是60度时
第二种情况:当底角是60度时
(不可以)
(可以)
(不可以)
已知: ⊿ABC中,AB=AC, ∠ A=600。
求证: ⊿ ABC是等边三角形。
A
B
C
证明:∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴∠B+∠C=120°
∴ ∠B=∠C = 600
∴∠A=∠B=∠C
∴ ⊿ ABC是等边三角形
讨论:如果∠ B=600 或是 ∠ C=600 ,
它是等边三角形吗?
有一个角是 60°的等腰三角形是等边三角形。
A
B
C
几何语言:
∵ ∠B=600 AB=BC
∴△ABC是等边三角形
2. 三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角
形是等边三角形.
1.三边都相等的三角形是等边三角形.(定义)
一般三角形
等边三角形
A
B
C
等腰三角形
等边三角形
A
B
C
∵AB=BC=AC
∴△ABC是等边三角形
∵ ∠B=600 AB=BC
∴△ABC是等边三角形
∵ ∠A= ∠ B= ∠ C
∴△ABC是等边三角形
等边三角形的判定方法
辩一辩:根据条件判断下列三角形是否为等边三角形.
(1)
(2)
(6)
(5)
不
是
是
是
是
是
(4)
(3)
不一定
是
练习 如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C,
∴ ∠A= ∠ADE= ∠ AED,
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
证明:∵ △ABC 是等边三角形,
∴ ∠A =∠ABC =∠ACB =60°.
∵ DE∥BC,
∴ ∠ABC =∠ADE,
∠ACB =∠AED,
∴ ∠A =∠ADE =∠AED,
∴ △ADE 是等边三角形.
【变式1】若点D、E 在边AB、AC 的延长线上,且 DE∥BC,结论还成立吗?
A
D
E
B
C
【变式2】若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E,
∴ ∠EAD =∠D =∠E,
∴ △ADE 是等边三角形.
A
D
E
B
C
【变式3】上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A==60°,
∵ AD=AE,
∴ △ADE是等腰三角形,
∴ △ADE是等边三角形.
同学们,这节课你有什么收获呢?
等边
三角形
定义
底=腰
性质
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
三边法
三角法
等腰三角形法
课堂总结
如图,等边三角形ABC中,AD是BC上的高,∠BDE= ∠CDF=60°,结合图形,图中有哪些与BD相等的线段?
相等的角?
等腰三角形?
等边三角形?
其他?
A
C
B
D
E
F
课下思考:
严格性之于数学家,犹如道德之于人。
证明的规范性在于:条理清晰,因果相应,言必有据。
这是初学证明者谨记和遵循的原则。
寄语
