九年级数学上册(人教版) 24.1.4(1) 圆周角-定理及推论1 教学课件(共24张PPT)
文档属性
| 名称 | 九年级数学上册(人教版) 24.1.4(1) 圆周角-定理及推论1 教学课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 17:23:33 | ||
图片预览



文档简介
(共24张PPT)
人教版九年级(上)数学教学课件
第24章 圆
24.1 圆的有关性质
情境导入
探究新知
当堂训练
典例精讲
知识归纳
24.1.4(1) 圆周角-定理及推论1
情境导入
温故知新
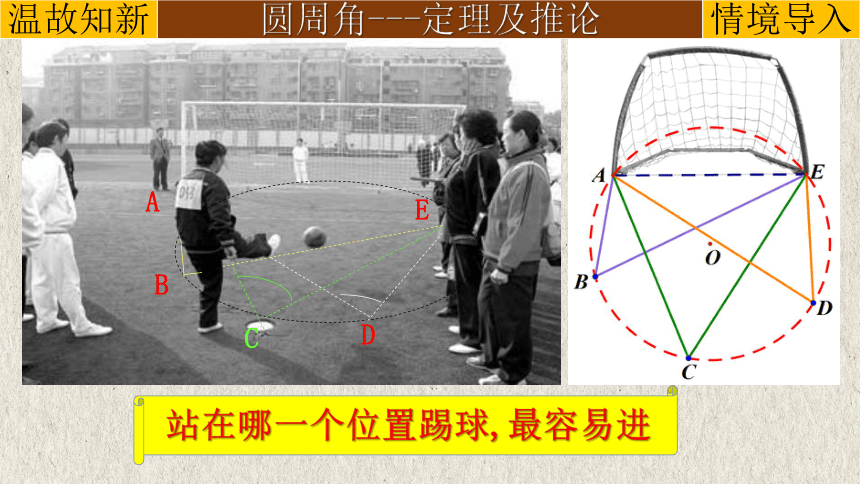
圆周角---定理及推论
C
A
E
D
B
站在哪一个位置踢球,最容易进
圆周角的定义
01
圆周角定理
02
圆周角定理的推论1
03
知识要点
精讲精练
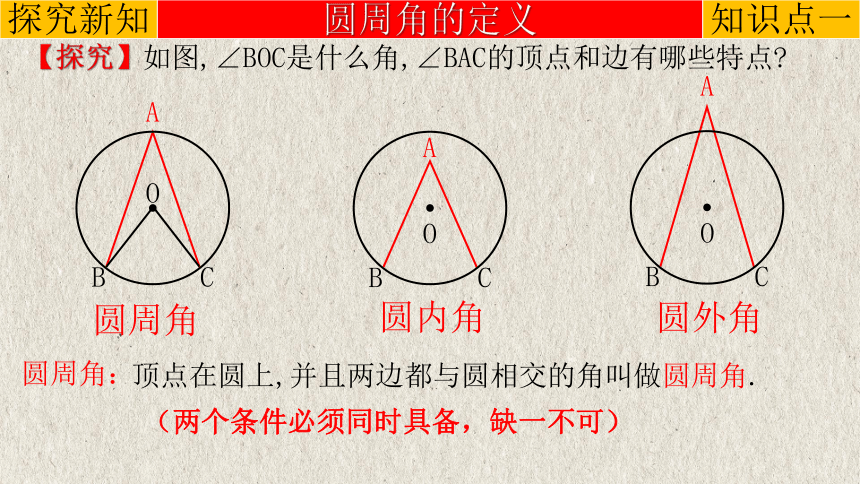
【探究】如图,∠BOC是什么角,∠BAC的顶点和边有哪些特点
A
C
O
B
A
C
O
B
A
C
O
B
(两个条件必须同时具备,缺一不可)
圆周角
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
知识点一
探究新知
圆周角的定义
圆内角
圆外角
圆周角:
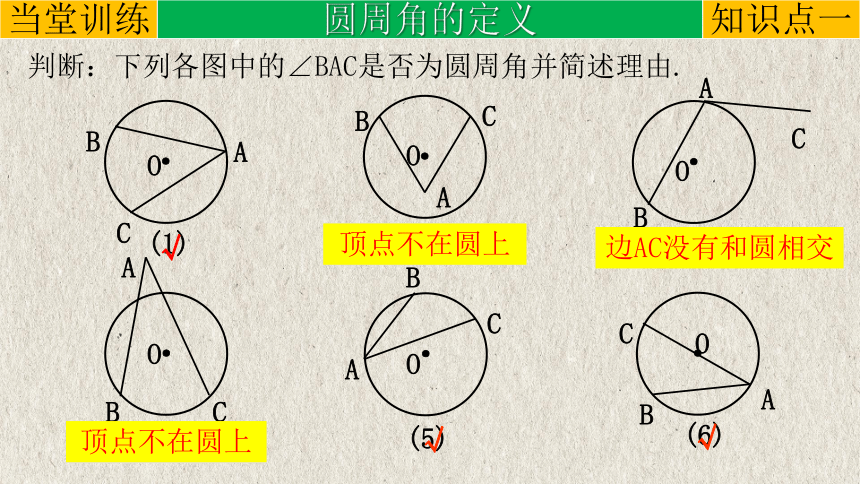
判断:下列各图中的∠BAC是否为圆周角并简述理由.
·
C
O
B
A
(2)
·
C
O
B
A
(1)
·
C
O
A
B
(3)
·
C
O
B
A
(5)
·
C
O
A
B
(6)
顶点不在圆上
边AC没有和圆相交
√
√
√
知识点一
当堂训练
圆周角的定义
·
C
O
B
A
(4)
顶点不在圆上
圆周角的定义
01
圆周角定理
02
圆周角定理的推论1
03
知识要点
精讲精练
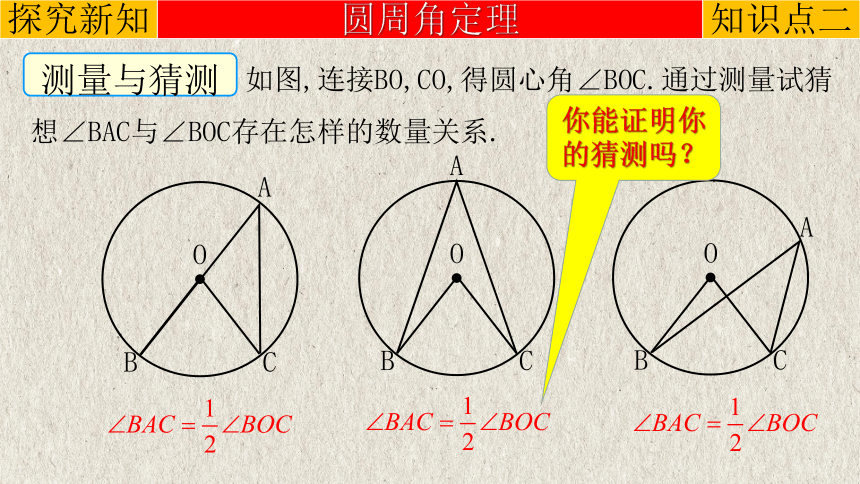
如图,连接BO,CO,得圆心角∠BOC.通过测量试猜想∠BAC与∠BOC存在怎样的数量关系.
测量与猜测
A
C
O
B
A
C
O
B
A
C
O
B
你能证明你的猜测吗?
知识点二
探究新知
圆周角定理
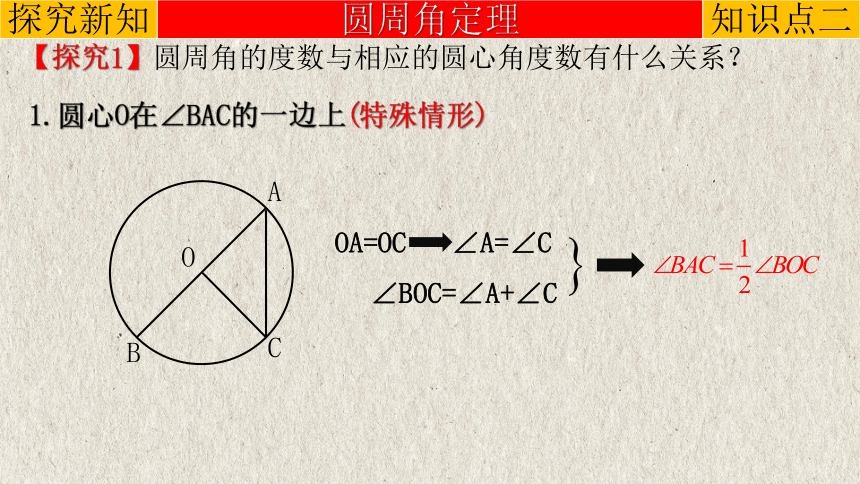
1.圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A=∠C
∠BOC=∠A+∠C
【探究1】圆周角的度数与相应的圆心角度数有什么关系?
A
C
B
O
知识点二
探究新知
圆周角定理
O
A
B
D
O
A
B
C
O
A
C
D
O
A
B
D
D
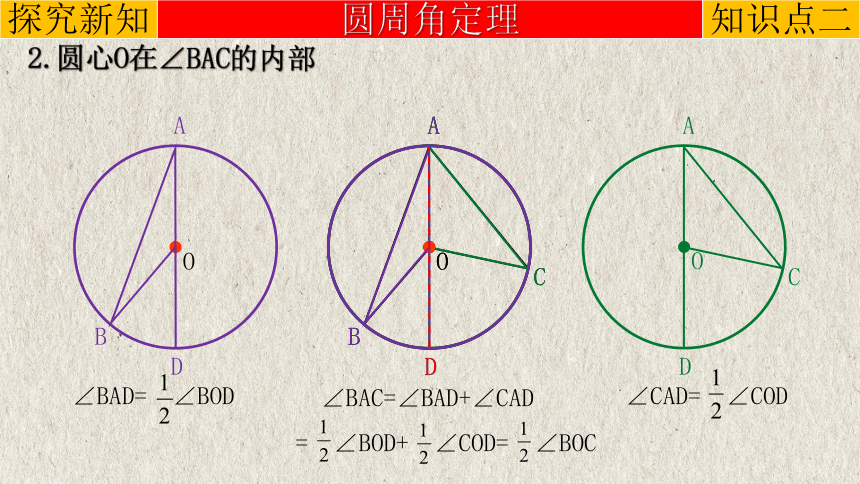
2.圆心O在∠BAC的内部
知识点二
探究新知
圆周角定理
∠CAD= ∠COD
∠BAD= ∠BOD
∠BAC=∠BAD+∠CAD
= ∠BOD+ ∠COD= ∠BOC
O
A
C
D
O
A
B
C
O
A
D
C
O
A
B
D
知识点二
探究新知
圆周角定理
O
A
D
C
3.圆心O在∠BAC的外部
D
O
A
B
D
∠CAD= ∠COD
∠BAD= ∠BOD
∠BAC=∠CAD-∠BAD
= ∠COD- ∠BOD = ∠BOC
圆周角定理:
A
C
O
B
A
C
O
B
一条弧所对的圆周角等于它所对圆心角的一半.
知识点二
知识归纳
圆周角定理
A
C
O
B
推导格式:
∴
∵BC=BC.
︵
︵
【例1】在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100) 和(5x-30) ,求这条弧所对的圆心角和圆周角的度数。
知识点二
典例精讲
圆周角定理
解:由题意得:
2x+100=2(5x-30)
解得:x=20
∴2x+100=140 ,5x-30=70 .
答:这条弧所对的圆心角和圆周角的度数分别为:140 和70 .
1.如图,已知CD是⊙O的直径,⊙O的弦AB⊥CD于点E,若∠AOD=60 ,则∠BCD的度数为( )
A.30 B.40 C.50 D.60
2.已知△ABC的三个顶点在⊙O上,∠BAC=50 ,
∠ABC=47 ,∠AOB=______.
A
A
E
O
B
C
D
166
B
A
C
O
知识点二
针对训练
圆周角定理
圆周角的定义
01
圆周角定理
02
圆周角定理的推论1
03
知识要点
精讲精练
1.如图1,∠D,∠C,∠E是什么角?它们对的弧是那条弧?
O
E
C
D
B
A
图1
知识点三
探究新知
圆周角定理的推论 1
2.∠D,∠C,∠E有什么大小关系?
3.把你得出的结论用文字描述出来.
同弧所对的圆周角相等.
5.把你得出的结论用文字描述出来.
等弧所对的圆周角相等.
4.如图2,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.若AB=AD,则∠BDA与∠CDA是否相等,为什么?
︵
︵
A
C
B
D
O
图2
圆周角定理推论1:
在同圆或等圆中,相等的圆周角所对的弧相等.
同弧或等弧所对的圆周角相等.
知识点三
知识归纳
圆周角定理的推论 1
O
E
C
D
B
A
图1
A
C
B
D
O
图2
推导格式:
∴∠C=∠D
∵AB=AB.
︵
︵
∵∠C=∠D
∴AB=AB.
︵
︵
【例3】在⊙O中,∠CBD=30 ,∠BDC=20 .求∠BAD的度数.
O
A
B
D
C
知识点三
典例精讲
圆周角定理的推论 1
解:连接AC.
∴∠BAC=∠BDC=20 ,∠CAD=∠CBD=30 .
∴∠BAD=∠BAC+∠CAD=50 .
∵BC=BC,CD=CD.
︵
︵
︵
︵
C
A
E
D
B
站在哪一个位置踢球,最容易进。
知识点三
当堂训练
圆周角定理的推论 1
1.判断:(1)同一个圆中等弧所对的圆周角相等( )
(2)相等的弦所对的圆周角也相等 ( )
2.若∠A=44 ,则∠O=____.∠D=____.若∠O=44 ,则∠D=____.
3.如图,点A,B,C,D在同一个圆上,AC,BD为四边形ABCD的对角线.
完成下列填空∠1=_____.∠2=_____.∠3=_____.∠5=____.
√
×
88
22
44
∠4
∠8
∠6
∠7
O
A
B
C
D
A
B
C
D
O
1
4
5
6
7
8
3
2
知识点三
当堂训练
圆周角定理的推论 1
4.船在航行过程中,船长通过测定角数来确定是否遇到暗礁,如图,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”,当船位于安全区域时,∠α与“危险角”有怎样的大小关系
解:当船位于安全区域时,即船位于暗礁区域外(即⊙O外),与两个灯塔的夹角∠α小于“危险角”.
A
F
E
O
P
C
B
α
知识点三
当堂训练
圆周角定理的推论 1
知识梳理
课堂小结
圆周角---定理及推论
圆周角
圆周角
定理
推论
1.顶点在圆上
2.两边都与圆相交的角
同弧或等弧所对的圆周角等于该弧所对的圆心角的一半;
同弧或等弧所对的圆周角相等;
相等的圆周角所对的弧相等.
圆周角
强
化
训
练
1.如图,在☉O中,已知直径AB⊥CD于点E,∠CDB=18 .将△OBD绕点O顺时针旋转,且旋转后点B,D的对应点分别是B ,D ,使弦B D 的一个端点与弦AC的一个端点恰好重合,则弦B D 与弦AC的夹角为___________.
2.如图,⊙O的直径AB=8,∠CBD=30 ,则CD=_____.
54 或90
A
E
B
D
C
O
提升能力
强化训练
圆周角---定理及推论
A
B
O
C
D
4
2.(一题多解)如图,已知AB、CD是⊙O中互相垂直的两条直径,又两条弦AE、CF垂直相交与点G,试证明:AE=CF
提升能力
强化训练
圆周角---定理及推论
O
C
D
G
E
F
B
A
人教版九年级(上)数学教学课件
第24章 圆
24.1 圆的有关性质
情境导入
探究新知
当堂训练
典例精讲
知识归纳
24.1.4(1) 圆周角-定理及推论1
情境导入
温故知新
圆周角---定理及推论
C
A
E
D
B
站在哪一个位置踢球,最容易进
圆周角的定义
01
圆周角定理
02
圆周角定理的推论1
03
知识要点
精讲精练
【探究】如图,∠BOC是什么角,∠BAC的顶点和边有哪些特点
A
C
O
B
A
C
O
B
A
C
O
B
(两个条件必须同时具备,缺一不可)
圆周角
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
知识点一
探究新知
圆周角的定义
圆内角
圆外角
圆周角:
判断:下列各图中的∠BAC是否为圆周角并简述理由.
·
C
O
B
A
(2)
·
C
O
B
A
(1)
·
C
O
A
B
(3)
·
C
O
B
A
(5)
·
C
O
A
B
(6)
顶点不在圆上
边AC没有和圆相交
√
√
√
知识点一
当堂训练
圆周角的定义
·
C
O
B
A
(4)
顶点不在圆上
圆周角的定义
01
圆周角定理
02
圆周角定理的推论1
03
知识要点
精讲精练
如图,连接BO,CO,得圆心角∠BOC.通过测量试猜想∠BAC与∠BOC存在怎样的数量关系.
测量与猜测
A
C
O
B
A
C
O
B
A
C
O
B
你能证明你的猜测吗?
知识点二
探究新知
圆周角定理
1.圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A=∠C
∠BOC=∠A+∠C
【探究1】圆周角的度数与相应的圆心角度数有什么关系?
A
C
B
O
知识点二
探究新知
圆周角定理
O
A
B
D
O
A
B
C
O
A
C
D
O
A
B
D
D
2.圆心O在∠BAC的内部
知识点二
探究新知
圆周角定理
∠CAD= ∠COD
∠BAD= ∠BOD
∠BAC=∠BAD+∠CAD
= ∠BOD+ ∠COD= ∠BOC
O
A
C
D
O
A
B
C
O
A
D
C
O
A
B
D
知识点二
探究新知
圆周角定理
O
A
D
C
3.圆心O在∠BAC的外部
D
O
A
B
D
∠CAD= ∠COD
∠BAD= ∠BOD
∠BAC=∠CAD-∠BAD
= ∠COD- ∠BOD = ∠BOC
圆周角定理:
A
C
O
B
A
C
O
B
一条弧所对的圆周角等于它所对圆心角的一半.
知识点二
知识归纳
圆周角定理
A
C
O
B
推导格式:
∴
∵BC=BC.
︵
︵
【例1】在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100) 和(5x-30) ,求这条弧所对的圆心角和圆周角的度数。
知识点二
典例精讲
圆周角定理
解:由题意得:
2x+100=2(5x-30)
解得:x=20
∴2x+100=140 ,5x-30=70 .
答:这条弧所对的圆心角和圆周角的度数分别为:140 和70 .
1.如图,已知CD是⊙O的直径,⊙O的弦AB⊥CD于点E,若∠AOD=60 ,则∠BCD的度数为( )
A.30 B.40 C.50 D.60
2.已知△ABC的三个顶点在⊙O上,∠BAC=50 ,
∠ABC=47 ,∠AOB=______.
A
A
E
O
B
C
D
166
B
A
C
O
知识点二
针对训练
圆周角定理
圆周角的定义
01
圆周角定理
02
圆周角定理的推论1
03
知识要点
精讲精练
1.如图1,∠D,∠C,∠E是什么角?它们对的弧是那条弧?
O
E
C
D
B
A
图1
知识点三
探究新知
圆周角定理的推论 1
2.∠D,∠C,∠E有什么大小关系?
3.把你得出的结论用文字描述出来.
同弧所对的圆周角相等.
5.把你得出的结论用文字描述出来.
等弧所对的圆周角相等.
4.如图2,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.若AB=AD,则∠BDA与∠CDA是否相等,为什么?
︵
︵
A
C
B
D
O
图2
圆周角定理推论1:
在同圆或等圆中,相等的圆周角所对的弧相等.
同弧或等弧所对的圆周角相等.
知识点三
知识归纳
圆周角定理的推论 1
O
E
C
D
B
A
图1
A
C
B
D
O
图2
推导格式:
∴∠C=∠D
∵AB=AB.
︵
︵
∵∠C=∠D
∴AB=AB.
︵
︵
【例3】在⊙O中,∠CBD=30 ,∠BDC=20 .求∠BAD的度数.
O
A
B
D
C
知识点三
典例精讲
圆周角定理的推论 1
解:连接AC.
∴∠BAC=∠BDC=20 ,∠CAD=∠CBD=30 .
∴∠BAD=∠BAC+∠CAD=50 .
∵BC=BC,CD=CD.
︵
︵
︵
︵
C
A
E
D
B
站在哪一个位置踢球,最容易进。
知识点三
当堂训练
圆周角定理的推论 1
1.判断:(1)同一个圆中等弧所对的圆周角相等( )
(2)相等的弦所对的圆周角也相等 ( )
2.若∠A=44 ,则∠O=____.∠D=____.若∠O=44 ,则∠D=____.
3.如图,点A,B,C,D在同一个圆上,AC,BD为四边形ABCD的对角线.
完成下列填空∠1=_____.∠2=_____.∠3=_____.∠5=____.
√
×
88
22
44
∠4
∠8
∠6
∠7
O
A
B
C
D
A
B
C
D
O
1
4
5
6
7
8
3
2
知识点三
当堂训练
圆周角定理的推论 1
4.船在航行过程中,船长通过测定角数来确定是否遇到暗礁,如图,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”,当船位于安全区域时,∠α与“危险角”有怎样的大小关系
解:当船位于安全区域时,即船位于暗礁区域外(即⊙O外),与两个灯塔的夹角∠α小于“危险角”.
A
F
E
O
P
C
B
α
知识点三
当堂训练
圆周角定理的推论 1
知识梳理
课堂小结
圆周角---定理及推论
圆周角
圆周角
定理
推论
1.顶点在圆上
2.两边都与圆相交的角
同弧或等弧所对的圆周角等于该弧所对的圆心角的一半;
同弧或等弧所对的圆周角相等;
相等的圆周角所对的弧相等.
圆周角
强
化
训
练
1.如图,在☉O中,已知直径AB⊥CD于点E,∠CDB=18 .将△OBD绕点O顺时针旋转,且旋转后点B,D的对应点分别是B ,D ,使弦B D 的一个端点与弦AC的一个端点恰好重合,则弦B D 与弦AC的夹角为___________.
2.如图,⊙O的直径AB=8,∠CBD=30 ,则CD=_____.
54 或90
A
E
B
D
C
O
提升能力
强化训练
圆周角---定理及推论
A
B
O
C
D
4
2.(一题多解)如图,已知AB、CD是⊙O中互相垂直的两条直径,又两条弦AE、CF垂直相交与点G,试证明:AE=CF
提升能力
强化训练
圆周角---定理及推论
O
C
D
G
E
F
B
A
同课章节目录
