九年级数学上册(人教版) 24.1.4(2) 圆周角-推论2,3及圆内接四边形 课件(共21张PPT)
文档属性
| 名称 | 九年级数学上册(人教版) 24.1.4(2) 圆周角-推论2,3及圆内接四边形 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
人教版九年级(上)数学教学课件
第24章 圆
24.1 圆的有关性质
情境导入
探究新知
当堂训练
典例精讲
知识归纳
24.1.4(2) 圆周角-推论2、3及圆内接四边形
圆周角定理的推论2、3
01
圆内接四边形定理
02
圆内接四边形定理的推论
03
知识要点
精讲精练
【探究】如图,线段AB是☉O的直径,点C是☉O上的任意一点(除点A、B外),那么,∠ACB就是直径AB所对的圆周角,∠ACB会是什么特殊角
·
O
A
C
B
解:∵OA=OB=OC,
∴∠OAC=∠OCA,∠OBC=∠OCB.
∵∠OAC+∠OBC+∠ACB=180 .
∴∠ACB=∠OCA+∠OCB=180 ÷2=90 .
知识点一
探究新知
圆周角定理的推论2、3
∴△AOC、△BOC都是等腰三角形.
·
O
A
C
B
圆周角定理推论2:
半圆(或直径)所对的圆周角是直角;
知识点一
知识归纳
圆周角定理的推论2、3
90 的圆周角所对的弦是直径.
推导格式:
∵AB是⊙O的直径,
∴∠C=90 ,
∴AB是⊙O的直径,
∵∠C=90 ,
一边的中线等于这边的一半的三角形是直角三角形.
圆周角定理推论3:
∴AD=BD=
【例1】如图,⊙O直径AB为10cm,弦AC为6cm.∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
A
C
B
D
O
知识点一
典例精讲
圆周角定理的推论2、3
解:连接OD,
∵AB是⊙O的直径,
在Rt△ABC中,BC=
∵CD平分 ACB,
∴ ACB= ADB=90 .
∴ ACD= BCD=45 ,
∴ AOD= BOD=90 ,
∴AD=BD
在Rt△ABD中,AD2+BD2=AB2,
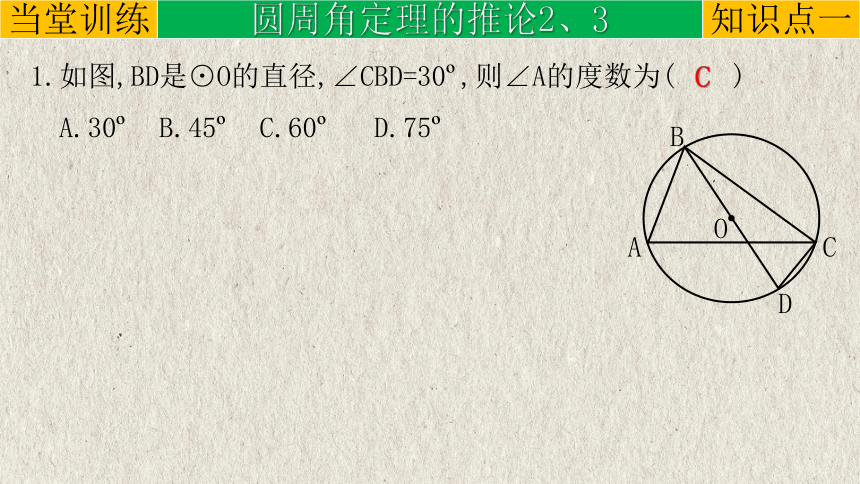
1.如图,BD是⊙O的直径,∠CBD=30 ,则∠A的度数为( )
A.30 B.45 C.60 D.75
C
A
O
C
D
B
知识点一
当堂训练
圆周角定理的推论2、3
圆周角定理的推论2、3
01
圆内接四边形定理
02
圆内接四边形定理的推论
03
知识要点
精讲精练
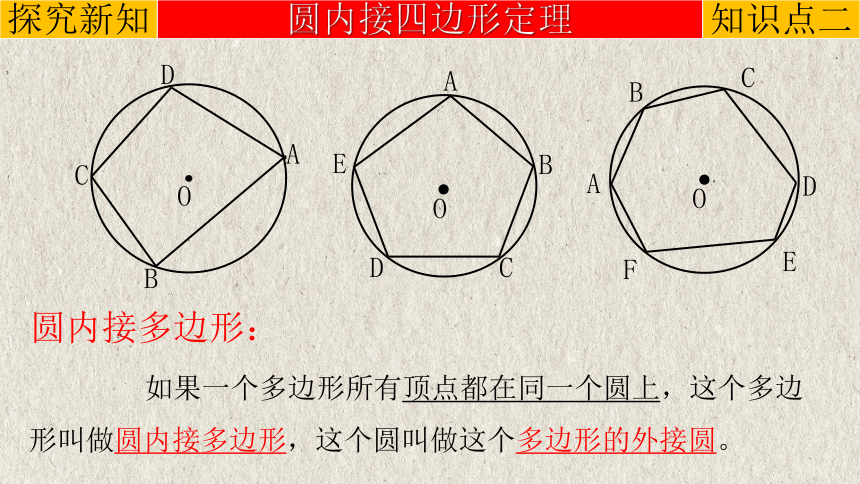
如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
圆内接多边形:
O
C
D
B
E
A
O
A
C
D
B
O
B
C
D
E
F
A
知识点二
探究新知
圆内接四边形定理
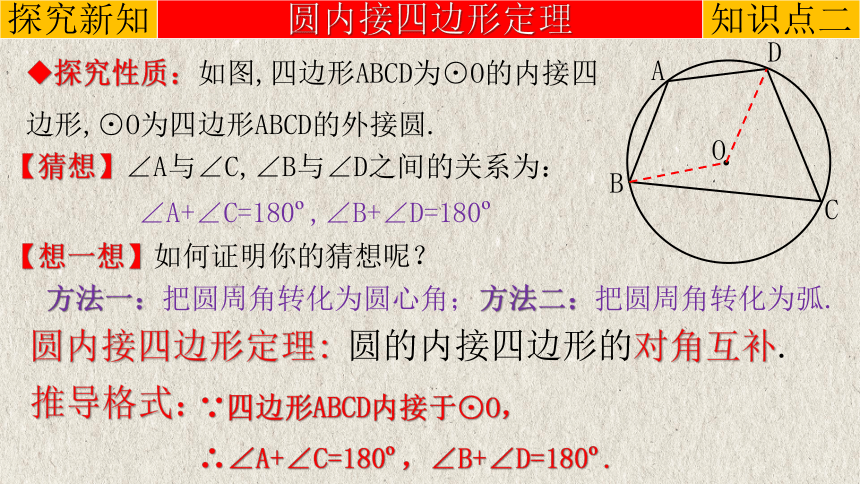
探究性质:如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
【猜想】∠A与∠C,∠B与∠D之间的关系为:
∠A+∠C=180 ,∠B+∠D=180
【想一想】如何证明你的猜想呢?
A
O
C
B
D
方法一:把圆周角转化为圆心角;
方法二:把圆周角转化为弧.
知识点二
探究新知
圆内接四边形定理
圆内接四边形定理:
推导格式:
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180 ,∠B+∠D=180 .
圆的内接四边形的对角互补.
【例2】若四边形ABCD为圆内接四边形,则∠A:∠B:∠C:∠D=( )
A.1:2:3:4 B.2:1:3:4 C.3:2:1:4 D.4:3:2:1
B
知识点二
典例精讲
圆内接四边形定理
1.如图,在⊙O中,∠BOD=120 ,那么∠BCD是( )
A.120 B.100 C.80 D.60
2.四边形ABCD是⊙O的内接四边形,且∠A=110 ,
∠B=80 ,则∠C= ,∠D= .
3.四边形ABCD内接于⊙O,∠A:∠C=1:3,则∠A=_____.
4.四边形ABCD内接于⊙O,AC垂直平分BD,∠BAC=40 ,则∠BCD=___
A
70
100
45
100
B
O
D
A
C
知识点二
当堂训练
圆内接四边形定理
C
O
D
B
A
E
想一想
图中∠A与∠DCE的大小有何关系?
圆内接四边形定理推论:
圆的内接四边形的任何一个外角都等于它的内对角.
推导格式:
∵四边形ABCD内接于⊙O.
∴∠DCE=∠A.
知识点三
探究新知
圆内接四边形定理的推论
【例3】如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G.
求证:∠FGD=∠ADC.
证明:∵AB为⊙O的直径,CF⊥AB于E,
O
D
E
G
A
B
C
F
知识点三
典例精讲
圆内接四边形定理的推论
∴∠FGD=∠ADC.
∴∠FGD=∠ACD.
∴弧AC=弧AD,
∴∠ADC=∠ACD,
∵四边形ACDG内接于⊙O,
如图,四边形ABCD内接于⊙O,若∠BOD=138 ,则它的外角∠DCE等于( ) A.69 B.42 C.48 D.38
A
D
C
B
E
O
A
知识点三
当堂训练
圆内接四边形定理的推论
推论2
推论3
圆内接
四边形
知识梳理
课堂小结
圆周角推论2、3及圆内接四边形
半圆(或直径)所对的圆周角是直角;
90 的圆周角所对的弦是直径.
定理:圆内接四边形的对角互补.
推论:圆内接四边形的任何一角的外角
都等于它的内对角.
圆周角
强
化
训
练
1.如图,AB是⊙O的直径,C,D在⊙O上,∠ABD=40 ,则∠BCD=_____.
2.如图,△ABC内接于⊙O上,∠C=30 ,AB=2,则⊙O的半径是_____.
3.等边△ABC内接于⊙O,P是⊙O上的一点,且不与A、B重合,则∠APB=___________.
4.若弧BC的度数为100 ,点A在⊙上则∠BOC=___,∠BAC=________
50
A
B
O
C
D
C
A
B
O
2
查漏补缺
巩固训练
圆周角推论2、3及圆内接四边形
120 或60
100
50 或130
5.如图,AB是⊙O的直径,弦CD交AB于点P,∠ACD=60 ,∠ADC=70 .
求∠APC的度数.
解:连接BC,则∠ACB=90 ,
∴∠DCB=∠ACB-∠ACD=90 -60 =30 .
又∵∠BAD=∠DCB=30 ,
∴∠APC=∠BAD+∠ADC=30 +70 =100 .
O
A
D
C
P
B
查漏补缺
巩固训练
圆周角推论2、3及圆内接四边形
6.如图,在△ABC中,AB=AC,以AB为直径的圆交BC于D,交AC于E.
(1)BD与CD的大小有什么关系 为什么
(2)求证:
A
B
C
D
E
O
提升能力
强化训练
圆周角推论2、3及圆内接四边形
7.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠BCD=120 ,
BC=CD.
(1)求证:CD∥AB;
(2)求S△ACD:S△ABC的值.
A
O
C
D
B
提升能力
强化训练
圆周角推论2、3及圆内接四边形
8.如图⊙O1与⊙O2都经过A,B两点,经过点A的直线CD与⊙O1交于点C与⊙O2交于点D.经过点B的直线EF与⊙O1交于点E,与⊙O2交于点F.求证:CE∥DF
提升能力
强化训练
圆周角推论2、3及圆内接四边形
O2
O1
C
E
A
B
F
D
人教版九年级(上)数学教学课件
第24章 圆
24.1 圆的有关性质
情境导入
探究新知
当堂训练
典例精讲
知识归纳
24.1.4(2) 圆周角-推论2、3及圆内接四边形
圆周角定理的推论2、3
01
圆内接四边形定理
02
圆内接四边形定理的推论
03
知识要点
精讲精练
【探究】如图,线段AB是☉O的直径,点C是☉O上的任意一点(除点A、B外),那么,∠ACB就是直径AB所对的圆周角,∠ACB会是什么特殊角
·
O
A
C
B
解:∵OA=OB=OC,
∴∠OAC=∠OCA,∠OBC=∠OCB.
∵∠OAC+∠OBC+∠ACB=180 .
∴∠ACB=∠OCA+∠OCB=180 ÷2=90 .
知识点一
探究新知
圆周角定理的推论2、3
∴△AOC、△BOC都是等腰三角形.
·
O
A
C
B
圆周角定理推论2:
半圆(或直径)所对的圆周角是直角;
知识点一
知识归纳
圆周角定理的推论2、3
90 的圆周角所对的弦是直径.
推导格式:
∵AB是⊙O的直径,
∴∠C=90 ,
∴AB是⊙O的直径,
∵∠C=90 ,
一边的中线等于这边的一半的三角形是直角三角形.
圆周角定理推论3:
∴AD=BD=
【例1】如图,⊙O直径AB为10cm,弦AC为6cm.∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
A
C
B
D
O
知识点一
典例精讲
圆周角定理的推论2、3
解:连接OD,
∵AB是⊙O的直径,
在Rt△ABC中,BC=
∵CD平分 ACB,
∴ ACB= ADB=90 .
∴ ACD= BCD=45 ,
∴ AOD= BOD=90 ,
∴AD=BD
在Rt△ABD中,AD2+BD2=AB2,
1.如图,BD是⊙O的直径,∠CBD=30 ,则∠A的度数为( )
A.30 B.45 C.60 D.75
C
A
O
C
D
B
知识点一
当堂训练
圆周角定理的推论2、3
圆周角定理的推论2、3
01
圆内接四边形定理
02
圆内接四边形定理的推论
03
知识要点
精讲精练
如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
圆内接多边形:
O
C
D
B
E
A
O
A
C
D
B
O
B
C
D
E
F
A
知识点二
探究新知
圆内接四边形定理
探究性质:如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
【猜想】∠A与∠C,∠B与∠D之间的关系为:
∠A+∠C=180 ,∠B+∠D=180
【想一想】如何证明你的猜想呢?
A
O
C
B
D
方法一:把圆周角转化为圆心角;
方法二:把圆周角转化为弧.
知识点二
探究新知
圆内接四边形定理
圆内接四边形定理:
推导格式:
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180 ,∠B+∠D=180 .
圆的内接四边形的对角互补.
【例2】若四边形ABCD为圆内接四边形,则∠A:∠B:∠C:∠D=( )
A.1:2:3:4 B.2:1:3:4 C.3:2:1:4 D.4:3:2:1
B
知识点二
典例精讲
圆内接四边形定理
1.如图,在⊙O中,∠BOD=120 ,那么∠BCD是( )
A.120 B.100 C.80 D.60
2.四边形ABCD是⊙O的内接四边形,且∠A=110 ,
∠B=80 ,则∠C= ,∠D= .
3.四边形ABCD内接于⊙O,∠A:∠C=1:3,则∠A=_____.
4.四边形ABCD内接于⊙O,AC垂直平分BD,∠BAC=40 ,则∠BCD=___
A
70
100
45
100
B
O
D
A
C
知识点二
当堂训练
圆内接四边形定理
C
O
D
B
A
E
想一想
图中∠A与∠DCE的大小有何关系?
圆内接四边形定理推论:
圆的内接四边形的任何一个外角都等于它的内对角.
推导格式:
∵四边形ABCD内接于⊙O.
∴∠DCE=∠A.
知识点三
探究新知
圆内接四边形定理的推论
【例3】如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G.
求证:∠FGD=∠ADC.
证明:∵AB为⊙O的直径,CF⊥AB于E,
O
D
E
G
A
B
C
F
知识点三
典例精讲
圆内接四边形定理的推论
∴∠FGD=∠ADC.
∴∠FGD=∠ACD.
∴弧AC=弧AD,
∴∠ADC=∠ACD,
∵四边形ACDG内接于⊙O,
如图,四边形ABCD内接于⊙O,若∠BOD=138 ,则它的外角∠DCE等于( ) A.69 B.42 C.48 D.38
A
D
C
B
E
O
A
知识点三
当堂训练
圆内接四边形定理的推论
推论2
推论3
圆内接
四边形
知识梳理
课堂小结
圆周角推论2、3及圆内接四边形
半圆(或直径)所对的圆周角是直角;
90 的圆周角所对的弦是直径.
定理:圆内接四边形的对角互补.
推论:圆内接四边形的任何一角的外角
都等于它的内对角.
圆周角
强
化
训
练
1.如图,AB是⊙O的直径,C,D在⊙O上,∠ABD=40 ,则∠BCD=_____.
2.如图,△ABC内接于⊙O上,∠C=30 ,AB=2,则⊙O的半径是_____.
3.等边△ABC内接于⊙O,P是⊙O上的一点,且不与A、B重合,则∠APB=___________.
4.若弧BC的度数为100 ,点A在⊙上则∠BOC=___,∠BAC=________
50
A
B
O
C
D
C
A
B
O
2
查漏补缺
巩固训练
圆周角推论2、3及圆内接四边形
120 或60
100
50 或130
5.如图,AB是⊙O的直径,弦CD交AB于点P,∠ACD=60 ,∠ADC=70 .
求∠APC的度数.
解:连接BC,则∠ACB=90 ,
∴∠DCB=∠ACB-∠ACD=90 -60 =30 .
又∵∠BAD=∠DCB=30 ,
∴∠APC=∠BAD+∠ADC=30 +70 =100 .
O
A
D
C
P
B
查漏补缺
巩固训练
圆周角推论2、3及圆内接四边形
6.如图,在△ABC中,AB=AC,以AB为直径的圆交BC于D,交AC于E.
(1)BD与CD的大小有什么关系 为什么
(2)求证:
A
B
C
D
E
O
提升能力
强化训练
圆周角推论2、3及圆内接四边形
7.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠BCD=120 ,
BC=CD.
(1)求证:CD∥AB;
(2)求S△ACD:S△ABC的值.
A
O
C
D
B
提升能力
强化训练
圆周角推论2、3及圆内接四边形
8.如图⊙O1与⊙O2都经过A,B两点,经过点A的直线CD与⊙O1交于点C与⊙O2交于点D.经过点B的直线EF与⊙O1交于点E,与⊙O2交于点F.求证:CE∥DF
提升能力
强化训练
圆周角推论2、3及圆内接四边形
O2
O1
C
E
A
B
F
D
同课章节目录
