人教版数学九年级下册 27.2.2 相似三角形的性质 课件(共21张PPT)
文档属性
| 名称 | 人教版数学九年级下册 27.2.2 相似三角形的性质 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 469.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 17:29:14 | ||
图片预览





文档简介
(共21张PPT)
第27章 相似
27.2 相似三角形
27.2.2 相似三角形的性质
猜想和探究
1.相似三角形有哪些判定定理?相似三角形的边和角分别有什么性质?
2.全等三角形的对应线段——对应中线、对应角平分线和对应高线各有什么性质?
判定定理: (1)三边成比例的两个三角形相似.
(2)两边成比例且夹角相等的两个三角形相似.
(3)两角分别相等的两个三角形相似.
性质: (1)对应边成比例; (2)对应角相等.
猜想:相似三角形的对应中线、对应角平分线和对应高线有何性质?
性质:全等三角形的对应中线、对应角平分线及对应高线都分别相等.
A'
B'
D'
C'
A
B
D
C
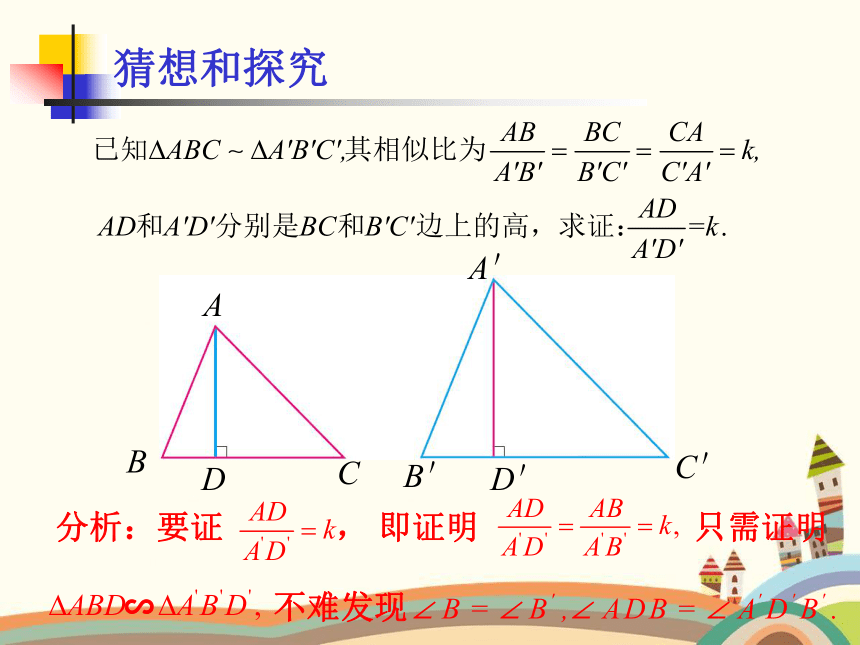
猜想和探究
分析:要证 , 即证明 只需证明
∽ 不难发现
结论1: 两个相似三角形对应高的比等于相似比.
试一试:请仿照上述方法猜想并证明两个相似三角形对应中线、对应角平分线的性质.
猜想和探究
生成与挖掘
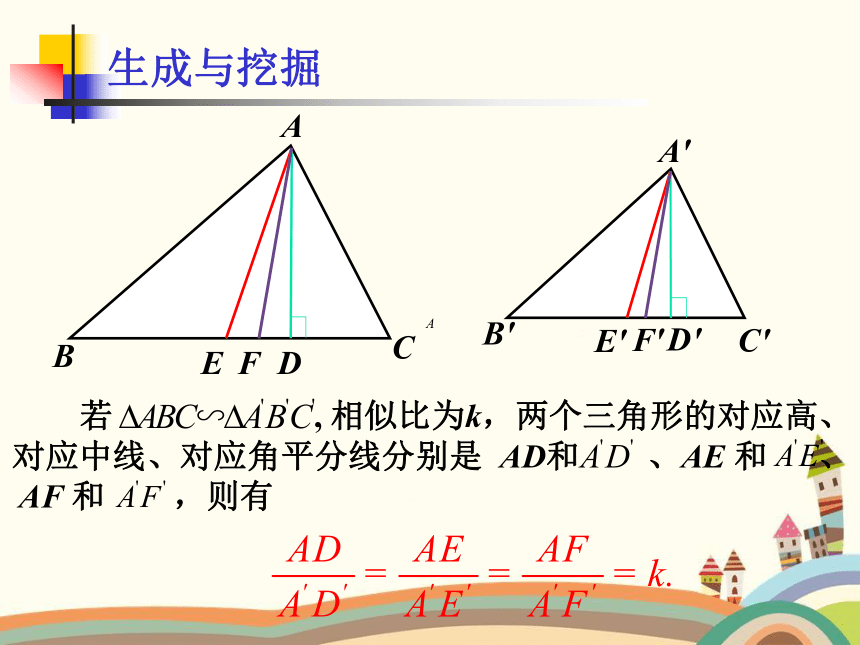
结论1:相似三角形的对应中线、对应角平分线、对应高的比都等于相似比.
1.根据你的猜想和证明,你发现相似三角形的对应中线、对应角平分线、对应高各有什么性质?请你用文字、图形和符号语言分别描述出来.
生成与挖掘
D
C
B
A
E
F
D'
B'
A′
C′
E′
F′
若 , 相似比为k,两个三角形的对应高、
对应中线、对应角平分线分别是 AD和 、AE 和 、
AF 和 ,则有
生成与挖掘
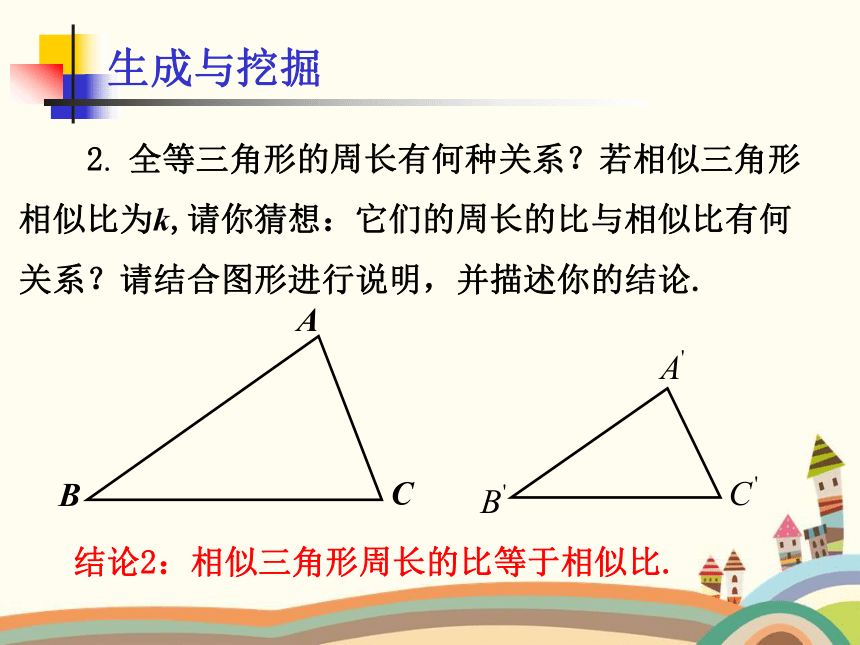
结论2:相似三角形周长的比等于相似比.
2. 全等三角形的周长有何种关系?若相似三角形
相似比为k,请你猜想:它们的周长的比与相似比有何
关系?请结合图形进行说明,并描述你的结论.
A
B
C
生成与挖掘
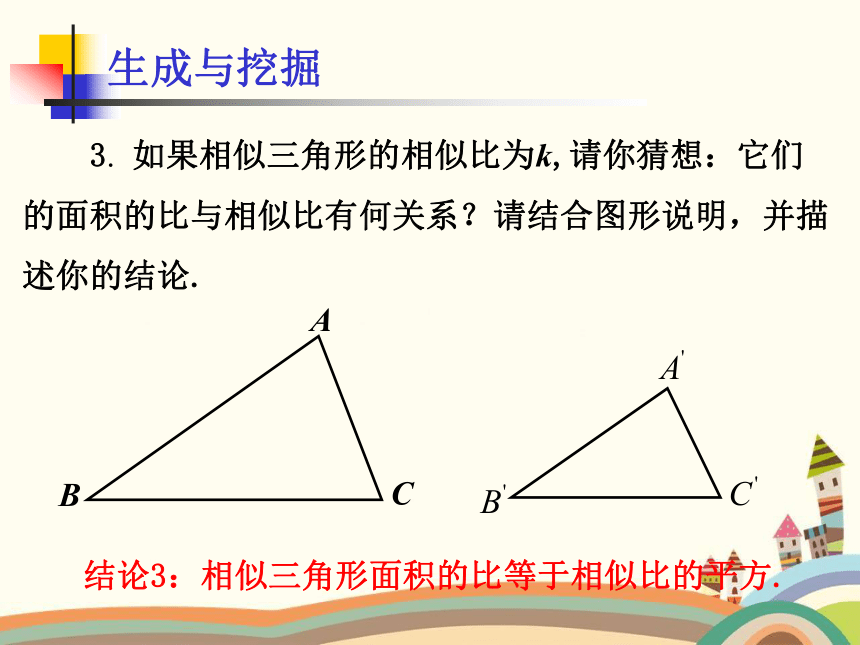
结论3:相似三角形面积的比等于相似比的平方.
3. 如果相似三角形的相似比为k,请你猜想:它们的面积的比与相似比有何关系?请结合图形说明,并描述你的结论.
A
B
C
生成与挖掘
相似三角形的性质:
如果两个相似三角形的相似比为k,则它们的对应线段(高、中线、角平分线)和周长的比都等于相似比,它们所对应面积的比等于相似比的平方.
辨析结论
1.判断题(正确的画“√”,错误的画“Χ”)
(1)一个三角形各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍;( )
(2)一个三角形各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍.( )
√
Χ
练习1:
例题与练习
例1 如图,在△ABC 和△DEF 中, AB=2DE ,AC=2DF,∠A=∠D.若△ABC 的边 BC 上的高为 6,
面积为 ,求△DEF 的边 EF 上的高和面积.
B
A
C
D
E
F
∵ △ABC 的边BC上的高是 6,面积是 ,
∴ △DEF 的边EF上的高为 ×6=3,
面积为
解:在△ABC 和△DEF 中,
∵AB=2DE,AC=2DF,
∴
又 ∠D=∠A ,
∴ △DEF∽△ABC ,
△DEF 与△ABC 的相似比为 .
例题与练习
练习2:
2.如图, △ABC∽△A′B′C′,AD,BE是△ABC的高, A′D′、 B′E′是△A′B′C′的高,求证
解:因为△ABC∽△A′B′C′,
AD、 A′D′是△ABC和△A′B′C′的高,
所以
同理
所以
例题与练习
练习2:
3.在一张复印出来的纸上,一个三角形的一条边由原图中的2 cm变成了6 cm,放缩比例是多少?这个三角形的面积发生了什么变化?
解:放缩比例是300%, 面积扩大为原来的9倍.
例题与练习
提高与拓展
例2 如图,在△ABC中, BA= BC=20 cm,AC=
30 cm,点P从A点出发,沿着AB以每秒4 cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3 cm的速度向A点运动,设运动时间为x 秒.
当x为何值时,PQ∥BC
如果△ABC与以点A,P,Q为
顶点的三角形相似,试求出它们的面积比.
提高与拓展
解:(1)由题意可知AP=4x,AQ=30- 3x.
因为 PQ∥BC,
所以
即
解得
提高与拓展
(2)当PQ∥BC时, ∽
由(1)可知
面积比为
当 ∠APQ= ∠ACB时, ∽
由
面积比为
提高与拓展
练习3:在△ABC中,AE ︰ EB=1 ︰ 2 ,EF∥BC , AD∥BC交CE 的延长线于D.求
答案:1 ︰6
课堂小结与作业布置
回顾思考:相似三角形有哪些性质?
1.从边的角度看:对应边的比等于相似比.
2.从角的角度看:对应角相等.
3.从对应线段的角度看:对应高、对应中线 、对应角平分线的比都等于相似比.
4.从周长和面积的角度看:对应周长的比等于相似
比,对应面积的比等于相似比的平方.
课堂小结:
课堂小结与作业布置
教材第42~43页习题27.2 第6,12题.
作业布置:
第27章 相似
27.2 相似三角形
27.2.2 相似三角形的性质
猜想和探究
1.相似三角形有哪些判定定理?相似三角形的边和角分别有什么性质?
2.全等三角形的对应线段——对应中线、对应角平分线和对应高线各有什么性质?
判定定理: (1)三边成比例的两个三角形相似.
(2)两边成比例且夹角相等的两个三角形相似.
(3)两角分别相等的两个三角形相似.
性质: (1)对应边成比例; (2)对应角相等.
猜想:相似三角形的对应中线、对应角平分线和对应高线有何性质?
性质:全等三角形的对应中线、对应角平分线及对应高线都分别相等.
A'
B'
D'
C'
A
B
D
C
猜想和探究
分析:要证 , 即证明 只需证明
∽ 不难发现
结论1: 两个相似三角形对应高的比等于相似比.
试一试:请仿照上述方法猜想并证明两个相似三角形对应中线、对应角平分线的性质.
猜想和探究
生成与挖掘
结论1:相似三角形的对应中线、对应角平分线、对应高的比都等于相似比.
1.根据你的猜想和证明,你发现相似三角形的对应中线、对应角平分线、对应高各有什么性质?请你用文字、图形和符号语言分别描述出来.
生成与挖掘
D
C
B
A
E
F
D'
B'
A′
C′
E′
F′
若 , 相似比为k,两个三角形的对应高、
对应中线、对应角平分线分别是 AD和 、AE 和 、
AF 和 ,则有
生成与挖掘
结论2:相似三角形周长的比等于相似比.
2. 全等三角形的周长有何种关系?若相似三角形
相似比为k,请你猜想:它们的周长的比与相似比有何
关系?请结合图形进行说明,并描述你的结论.
A
B
C
生成与挖掘
结论3:相似三角形面积的比等于相似比的平方.
3. 如果相似三角形的相似比为k,请你猜想:它们的面积的比与相似比有何关系?请结合图形说明,并描述你的结论.
A
B
C
生成与挖掘
相似三角形的性质:
如果两个相似三角形的相似比为k,则它们的对应线段(高、中线、角平分线)和周长的比都等于相似比,它们所对应面积的比等于相似比的平方.
辨析结论
1.判断题(正确的画“√”,错误的画“Χ”)
(1)一个三角形各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍;( )
(2)一个三角形各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍.( )
√
Χ
练习1:
例题与练习
例1 如图,在△ABC 和△DEF 中, AB=2DE ,AC=2DF,∠A=∠D.若△ABC 的边 BC 上的高为 6,
面积为 ,求△DEF 的边 EF 上的高和面积.
B
A
C
D
E
F
∵ △ABC 的边BC上的高是 6,面积是 ,
∴ △DEF 的边EF上的高为 ×6=3,
面积为
解:在△ABC 和△DEF 中,
∵AB=2DE,AC=2DF,
∴
又 ∠D=∠A ,
∴ △DEF∽△ABC ,
△DEF 与△ABC 的相似比为 .
例题与练习
练习2:
2.如图, △ABC∽△A′B′C′,AD,BE是△ABC的高, A′D′、 B′E′是△A′B′C′的高,求证
解:因为△ABC∽△A′B′C′,
AD、 A′D′是△ABC和△A′B′C′的高,
所以
同理
所以
例题与练习
练习2:
3.在一张复印出来的纸上,一个三角形的一条边由原图中的2 cm变成了6 cm,放缩比例是多少?这个三角形的面积发生了什么变化?
解:放缩比例是300%, 面积扩大为原来的9倍.
例题与练习
提高与拓展
例2 如图,在△ABC中, BA= BC=20 cm,AC=
30 cm,点P从A点出发,沿着AB以每秒4 cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3 cm的速度向A点运动,设运动时间为x 秒.
当x为何值时,PQ∥BC
如果△ABC与以点A,P,Q为
顶点的三角形相似,试求出它们的面积比.
提高与拓展
解:(1)由题意可知AP=4x,AQ=30- 3x.
因为 PQ∥BC,
所以
即
解得
提高与拓展
(2)当PQ∥BC时, ∽
由(1)可知
面积比为
当 ∠APQ= ∠ACB时, ∽
由
面积比为
提高与拓展
练习3:在△ABC中,AE ︰ EB=1 ︰ 2 ,EF∥BC , AD∥BC交CE 的延长线于D.求
答案:1 ︰6
课堂小结与作业布置
回顾思考:相似三角形有哪些性质?
1.从边的角度看:对应边的比等于相似比.
2.从角的角度看:对应角相等.
3.从对应线段的角度看:对应高、对应中线 、对应角平分线的比都等于相似比.
4.从周长和面积的角度看:对应周长的比等于相似
比,对应面积的比等于相似比的平方.
课堂小结:
课堂小结与作业布置
教材第42~43页习题27.2 第6,12题.
作业布置:
