【总复习】数学_必修四_平面向量_PPT
文档属性
| 名称 | 【总复习】数学_必修四_平面向量_PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 256.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-18 22:41:06 | ||
图片预览









文档简介
课件41张PPT。 必修四 平面向量
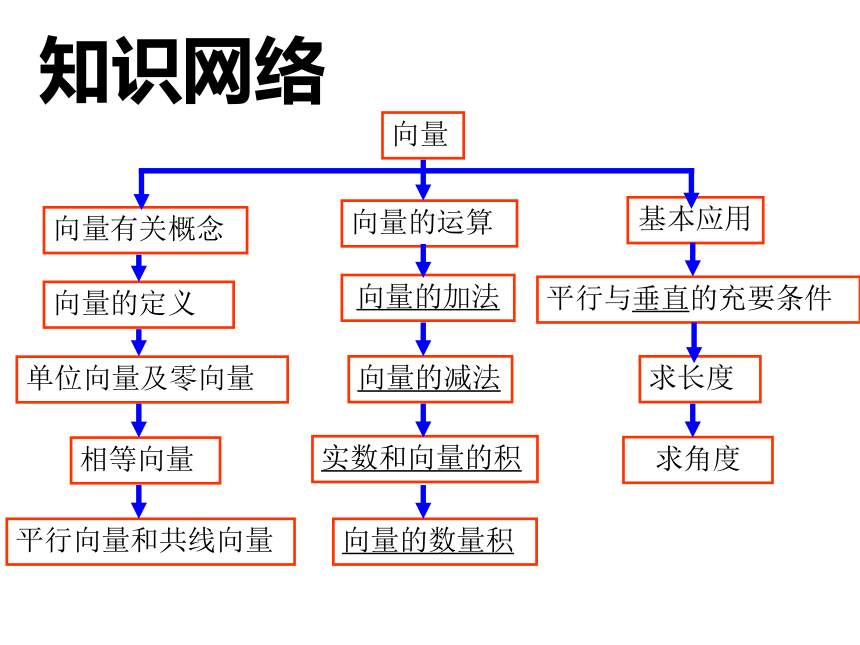
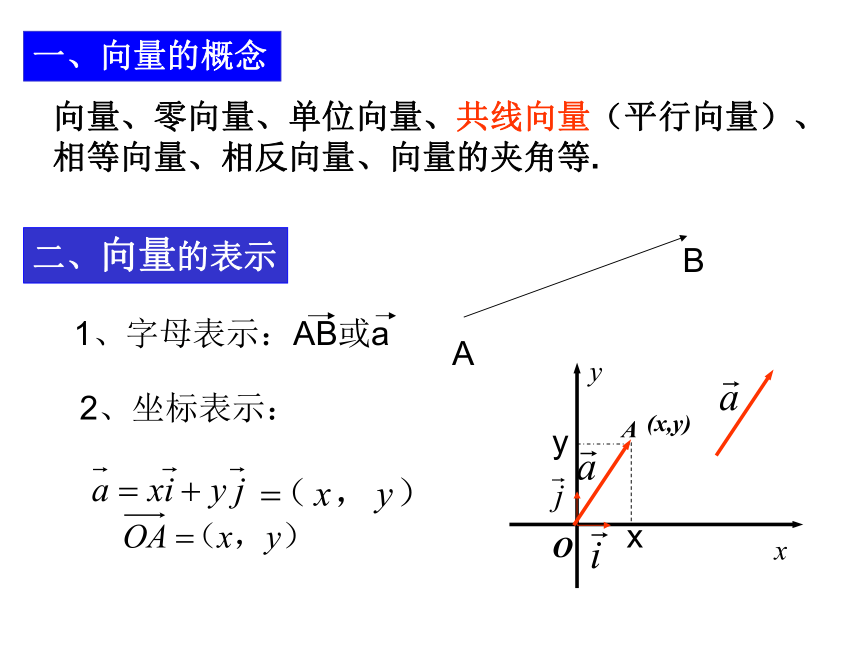
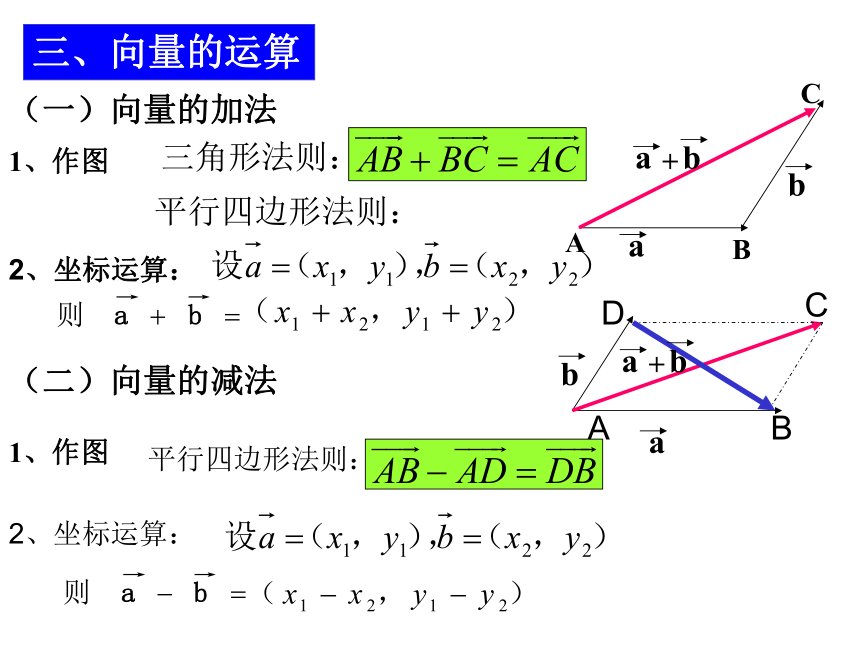
总 复 习知识网络向量、零向量、单位向量、共线向量(平行向量)、相等向量、相反向量、向量的夹角等.例1 e1、e2不共线,a=e1+e2 b=3e1-3e2
a与b是否共线。典型例题分析:例2 设a,b是两个不共线向量。AB=2a+kb BC=a+b CD=a-2b
A、B、D共线则k=_____(k∈R)例3、 已知a=(3,-2) b=(-2,1) c=(7,-4),用a、b表示c。例4、 |a|=10 b=(3,-4)且a∥b求a例5、 设|a|=|b|=1 |3a-2b|=3则|3a+b|=____法2 9=9a2+4b2-12a·b
∴a·b=
又,(3a+b)2=9a2+b2+6a·b=12
∴|3a+b|=2[解][例10][解析][例11][例11][解析][例12][解析]4、已知|a|=|b|=1,a与b的夹角为90。,c=2a+3b,d=ka-4b,c⊥d,k=()
A. -6 B. 6 C. 3 D. -3
5、设点A(a,b),B(c,d),若径平移得A(2a,2b),那么B点之新坐标为()
A. (2c,2d) B. (a+c,b+d)
C. (a+2c,b+2d) D. (2a+c,2b+d)
6、已知|a|=3,|b|=4,(a+b)·(a+3b)=33,则a与b的夹角为()
A. 30。 B. 60。 C. 120。 D. 150。
7.若|a-b|= ,|a|=4,|b|=5,则a·b=( )
A.10 B.-10 C.10 D.108、已知△ABC中,AB=a,AC=b,a·b<0,S△ABC= ,|a|=3,|b|=5,则a与b的夹角为()
A.30。B.-150。C.150。D.30。或150。
9、若点P分AB所成的比为 ,则A分BP所成的比是()
A. B. C. - D. -
10、在△ABC中,三内角A,B,C对应的三边分别为a,b,c,已知c=3,∠C=60。,a+b=5,则cos 的值是()
A. B. C. D.11、在△ABC中,若(a+c)(a-c)=b(b+c),则∠A=()
A.30。 B.60。 C.120。 D.150。
12、在△ABC中,已知角A、B、C的对边分别是a、b、c,且3b= asinB,
cosB=cosC,则△ABC的形状是()
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形二、填空题:
13、设a=(m+1)e1-3e2,b=e1+(m-1)e2,若(a+b)⊥(a-b),那么m=____。
14、单位向量e1,e2的夹角为60。,则(e1-2e2)·(-2e1+3e2)=______。
15、在△ABC中,若(a+b+c)(b+c-a)=3bc,则∠A=_____。
16、在△ABC中,a,b,c分别是角A,B,C的对边长,若(a+b+c)(sinA+sinB-sinC)=3asinB,则∠C=_______。三、解答题:
17、已知e1与e2是夹角为60。的单位向量,且a=2e1+e2,b=-3e1+2e2,求a·b及a与b的夹角α。
解:e1,e2是单位向量,且夹角为60。
∴e1e2=|e1||e2|cos60。=
∴ab=(2e1+e2)·(-3e1+2e2)
=-6|e12|+e1·e2+2e22=-3
而|a|2=a2=(2e1+e2)2=4e12+4e1e2+e22=7
|b|2=b2=(-3e1+2e2)2=9e12-12e1e2+4e22=7
|a|= |b|= ∴cosα= α=120。20、(1)已知a,b都是非零向量,且a+3b与7a-5b垂直,a-4b与7a-2b垂直,求a与b的夹角;(2)已知|a|= ,|b|= ,且a与b的夹角为 ,试求a+2b与a-b的夹角θ的大小。
解:(1)(a+3b)·(7a-5b)=0
(a-4b)·(7a-2b)=0
7a+16a·b-15b=0
7a2-30a·b+8b2=0
a2=b2 2a·b=b2
∴cosθ= θ=60。(2)a2=3 b2=4 |a|·|b|=2
a·b=|a|·|b|cosθ= ·cos30。=322、已知△ABC中,A(2,4),B(-1,-2),
C(4,3),BC边上的高为AD。
(1)求证:AB⊥AC;
(2)求点D和向量AD的坐标;
(3)求证:AD2=BD·DC
解:(1)A(2,4) B(-1,-2) C(4,3)
AB=(-3,-6) AC=(2,-1)
AB·AC=(-3)×2+(-6)×(-1)=0
AB⊥AC(3)AD=( ,- ) BD=( , )
DC=( , )
|AD|2= + =
BD·DC= + =
∴AD2=BD·DC
a与b是否共线。典型例题分析:例2 设a,b是两个不共线向量。AB=2a+kb BC=a+b CD=a-2b
A、B、D共线则k=_____(k∈R)例3、 已知a=(3,-2) b=(-2,1) c=(7,-4),用a、b表示c。例4、 |a|=10 b=(3,-4)且a∥b求a例5、 设|a|=|b|=1 |3a-2b|=3则|3a+b|=____法2 9=9a2+4b2-12a·b
∴a·b=
又,(3a+b)2=9a2+b2+6a·b=12
∴|3a+b|=2[解][例10][解析][例11][例11][解析][例12][解析]4、已知|a|=|b|=1,a与b的夹角为90。,c=2a+3b,d=ka-4b,c⊥d,k=()
A. -6 B. 6 C. 3 D. -3
5、设点A(a,b),B(c,d),若径平移得A(2a,2b),那么B点之新坐标为()
A. (2c,2d) B. (a+c,b+d)
C. (a+2c,b+2d) D. (2a+c,2b+d)
6、已知|a|=3,|b|=4,(a+b)·(a+3b)=33,则a与b的夹角为()
A. 30。 B. 60。 C. 120。 D. 150。
7.若|a-b|= ,|a|=4,|b|=5,则a·b=( )
A.10 B.-10 C.10 D.108、已知△ABC中,AB=a,AC=b,a·b<0,S△ABC= ,|a|=3,|b|=5,则a与b的夹角为()
A.30。B.-150。C.150。D.30。或150。
9、若点P分AB所成的比为 ,则A分BP所成的比是()
A. B. C. - D. -
10、在△ABC中,三内角A,B,C对应的三边分别为a,b,c,已知c=3,∠C=60。,a+b=5,则cos 的值是()
A. B. C. D.11、在△ABC中,若(a+c)(a-c)=b(b+c),则∠A=()
A.30。 B.60。 C.120。 D.150。
12、在△ABC中,已知角A、B、C的对边分别是a、b、c,且3b= asinB,
cosB=cosC,则△ABC的形状是()
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形二、填空题:
13、设a=(m+1)e1-3e2,b=e1+(m-1)e2,若(a+b)⊥(a-b),那么m=____。
14、单位向量e1,e2的夹角为60。,则(e1-2e2)·(-2e1+3e2)=______。
15、在△ABC中,若(a+b+c)(b+c-a)=3bc,则∠A=_____。
16、在△ABC中,a,b,c分别是角A,B,C的对边长,若(a+b+c)(sinA+sinB-sinC)=3asinB,则∠C=_______。三、解答题:
17、已知e1与e2是夹角为60。的单位向量,且a=2e1+e2,b=-3e1+2e2,求a·b及a与b的夹角α。
解:e1,e2是单位向量,且夹角为60。
∴e1e2=|e1||e2|cos60。=
∴ab=(2e1+e2)·(-3e1+2e2)
=-6|e12|+e1·e2+2e22=-3
而|a|2=a2=(2e1+e2)2=4e12+4e1e2+e22=7
|b|2=b2=(-3e1+2e2)2=9e12-12e1e2+4e22=7
|a|= |b|= ∴cosα= α=120。20、(1)已知a,b都是非零向量,且a+3b与7a-5b垂直,a-4b与7a-2b垂直,求a与b的夹角;(2)已知|a|= ,|b|= ,且a与b的夹角为 ,试求a+2b与a-b的夹角θ的大小。
解:(1)(a+3b)·(7a-5b)=0
(a-4b)·(7a-2b)=0
7a+16a·b-15b=0
7a2-30a·b+8b2=0
a2=b2 2a·b=b2
∴cosθ= θ=60。(2)a2=3 b2=4 |a|·|b|=2
a·b=|a|·|b|cosθ= ·cos30。=322、已知△ABC中,A(2,4),B(-1,-2),
C(4,3),BC边上的高为AD。
(1)求证:AB⊥AC;
(2)求点D和向量AD的坐标;
(3)求证:AD2=BD·DC
解:(1)A(2,4) B(-1,-2) C(4,3)
AB=(-3,-6) AC=(2,-1)
AB·AC=(-3)×2+(-6)×(-1)=0
AB⊥AC(3)AD=( ,- ) BD=( , )
DC=( , )
|AD|2= + =
BD·DC= + =
∴AD2=BD·DC
同课章节目录
