高中数学必修4复习

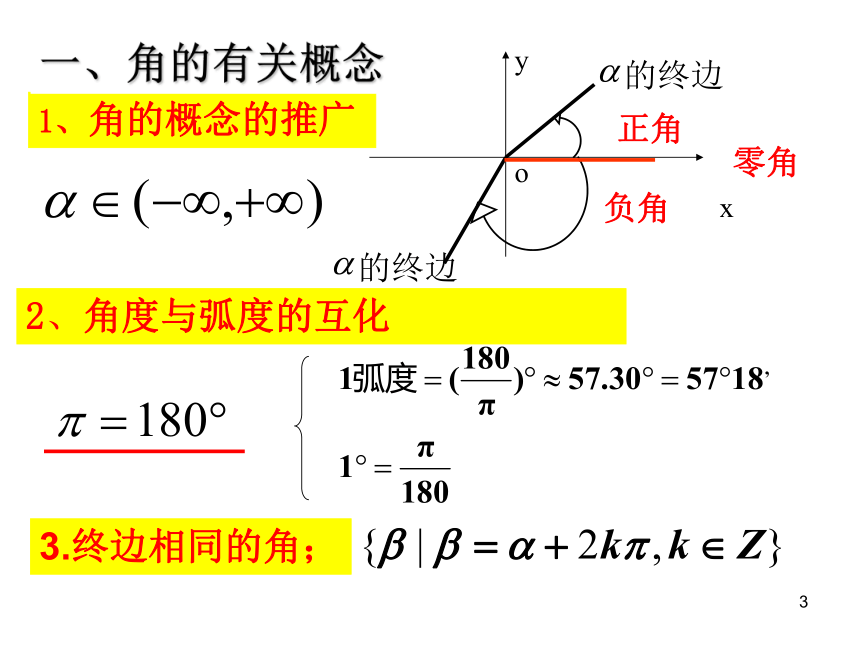
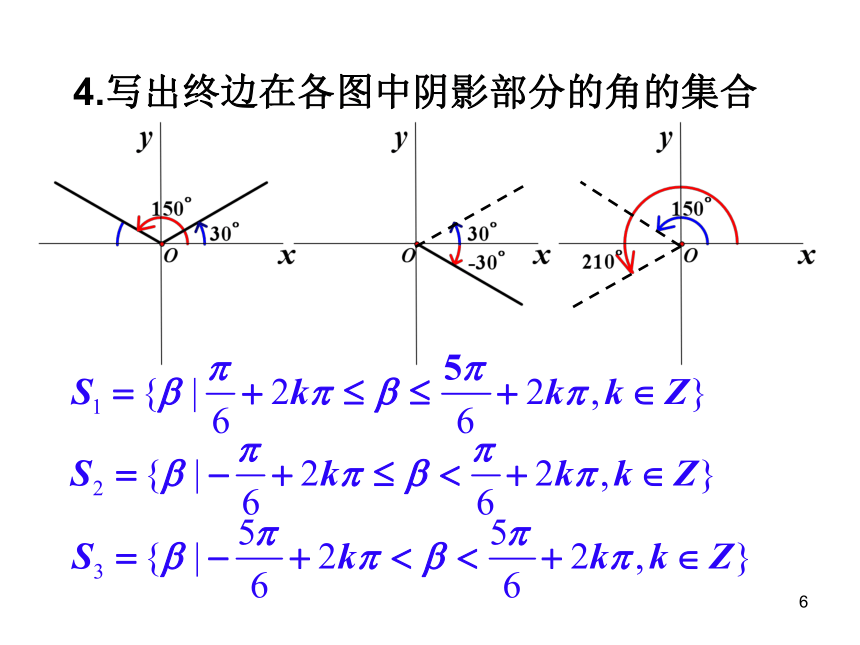
课件45张PPT。1必修四复习2三角函数部分31、角的概念的推广x一、角的有关概念2、角度与弧度的互化3.终边相同的角；4练习：2.分别写出满足下列条件的角的集合（1）终边在y轴上的角的集合（2）终边在象限角平分线上的角的集合53、角的终边落在“射线上”、“直线上”及“互相垂直的两条直线上”的一般表示式64.写出终边在各图中阴影部分的角的集合74.弧度制：(1)1弧度的角：长度等于半径的弧所对的圆心角.(2)弧长公式：(3)扇形面积公式：8已知一个扇形的周长是4cm,面积为1cm2，
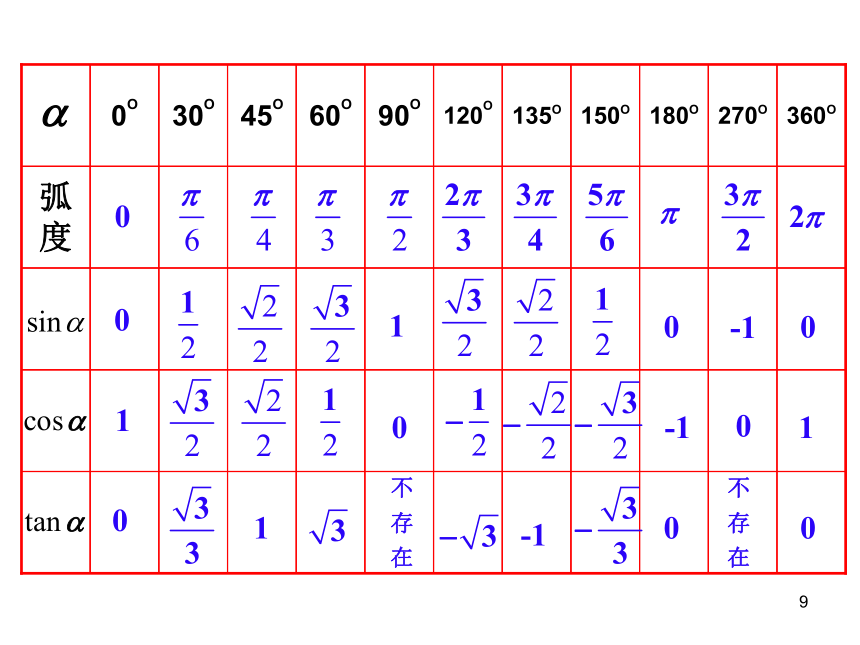
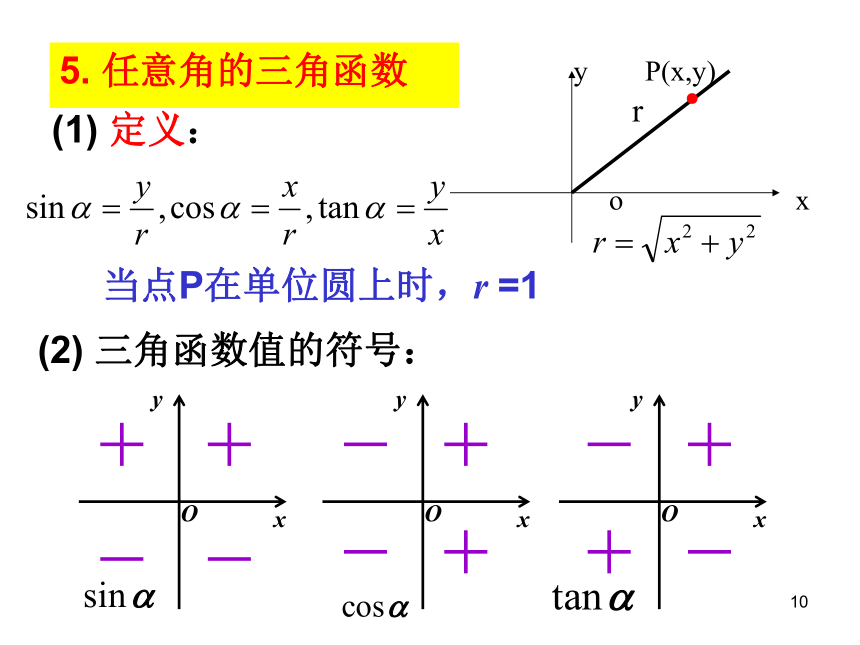
则这个扇形的圆心角的弧度数为_____________练习9105. 任意角的三角函数(1) 定义：(2) 三角函数值的符号：当点P在单位圆上时，r =1xyo●P(x,y)r116. 同角三角函数的基本关系式(1) 平方关系：(2) 商的关系：练习．已知tanα= ，求sinα.cosα 12练习13公式二：公式三：公式四：公式一(k∈Z)诱导公式记忆方法：奇变偶不变，符号看象限14公式五：公式六：公式七：公式八：诱导公式记忆方法：奇变偶不变，符号看象限15利用诱导公式把任意角的三角函数转化为
锐角三角函数,一般按下面步骤进行:用公式一
或公式三用公式一用公式二或四或五或六可概括为：“负化正，大化小，化到锐角为终了” 161,求值：练习17最高点：最低点：与x轴的交点：作图时的五个关键点18最高点：最低点：与x轴的交点：作图时的五个关键点19所有的点向左(? >0)
或向右(? <0)平行移动
| ? | 个单位长度y=sinxy=sin(x+?)y=sinxy=sin?x横坐标缩短(?>1)或
伸长(0< ?<1) 1/?倍纵坐标不变y=sinxy=Asinx纵坐标伸长(A>1)或
缩短(0< A<1) A倍横坐标不变 y=Asin（?x+ ?）y=sinx三角函数图象变换20y=sinxy=sin(x+?)横坐标缩短?>1 (伸长01 (缩短00 (向右?<0)方法1:按先平移后变周期的顺序变换平移|?|个单位纵坐标不变横坐标不变21y=sinx横坐标缩短?>1 (伸长01 (缩短00 (向右?<0)平移|?|/?个单位22总结:利用 ，求得23时，时，时，时，奇函数偶函数T=2π奇函数T=2πT=π24求函数 的单调递增区间:增增增减25练习26三角函数常规求值域问题27平面向量部分28既有大小又有方向的量叫向量或用有向线段表示29平行向量的定义： 长度（模）为1个单位长度的向量长度（模）为0的向量，记作 方向相同或相反的非零向量规定：零向量与任一向量平行30长度相等且方向相同的向量叫做相等向量任一组平行向量都可移到同一条直线上 所以平行向量也叫共线向量311.向量加法三角形法则:特点:首尾相接特点:共起点2.向量加法平行四边形法则:3.向量减法三角形法则:特点：共起点，连终点，方向指向被减数3233共线向量基本定理： 向量 与非零向量 共线当且仅当
有唯一一个实数 ，使得(2)证明三点共线的问题:定理的应用:(1)有关向量共线问题:(3)证明两直线平行的问题:34平面向量基本定理:如果 是同一平面内的两个不共线向量，那么对于这一平面内的任一向量 有且只有一对实数 ,使35向量的夹角:夹角的范围：注意:两向量必须是同起点的36坐标(x,y)向量 一个向量的坐标等于表示此向量的有向
线段的终点的坐标减去起点的坐标.重要结论37平面向量数量积3839(1)垂直:(2)平行:40解:设所求向量为(x, y), 则已知 =(4,3) ,求与 垂直的单位向量 .41B 练习C42D15.6.m=-2 练习437.A8. 练习4445