苏教版2019高中数学必修1 第8章8.2.1 几个函数模型的比较 课件(60张PPT)
文档属性
| 名称 | 苏教版2019高中数学必修1 第8章8.2.1 几个函数模型的比较 课件(60张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 09:25:07 | ||
图片预览










文档简介
(共60张PPT)
8.2.1 几个函数模型的比较
第8章 §8.2 函数与数学模型
学习目标
1.了解指数爆炸、对数增长等含义.
2.借助信息技术,作出函数图象,比较指数函数、对数函数以及幂函数的增长差异.
3.了解不同函数模型的“变化趋势”,加深对自然现象的理解.
导语
如果你现在手里有一笔资金可以用于投资,现在有三种投资方案供你选择,这三种方案的回报是这样的:方案一:每天回报40元;方案二:第一天回报10元,以后每天比前一天多回报10元;方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.请问,你会选择哪种投资方案?为了解决这个问题,让我们一起开始今天的探究吧!
一、指数爆炸(求值)
二、函数模型增长差异的比较(图象)
课时对点练
随堂演练
内容索引
指数爆炸(求值)
一
知识梳理
指数变化
当a>1时,指数函数y=ax随着x的增大而 ,且增大的速度越来越 ,呈“爆炸”的趋势,因此“指数增长”可以用“指数爆炸”来形容.
当0增大
快
减小
0
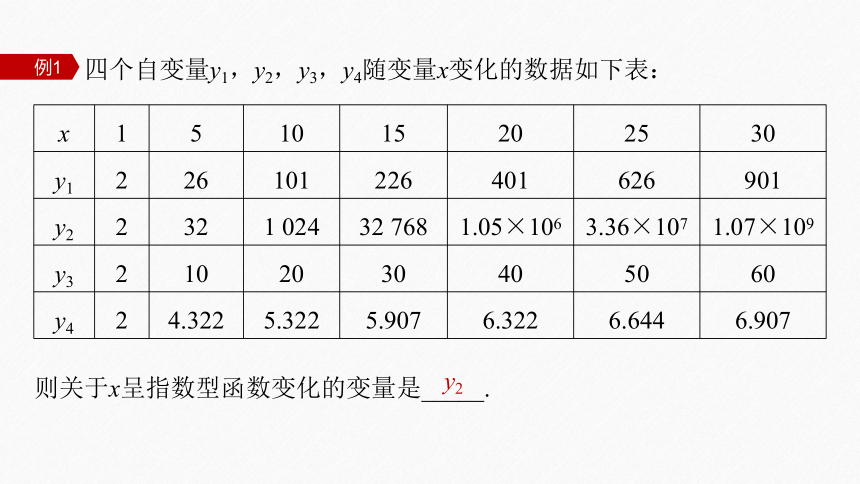
四个自变量y1,y2,y3,y4随变量x变化的数据如下表:
例1
x 1 5 10 15 20 25 30
y1 2 26 101 226 401 626 901
y2 2 32 1 024 32 768 1.05×106 3.36×107 1.07×109
y3 2 10 20 30 40 50 60
y4 2 4.322 5.322 5.907 6.322 6.644 6.907
则关于x呈指数型函数变化的变量是_____.
y2
以爆炸式增长的变量呈指数函数变化.从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,且都是越来越大,但是增长速度不同,其中变量y2的增长速度最快,画出它们的图象(图略),可知变量y2关于x呈指数型函数变化.
指数函数增长的特点
指数函数y=ax(a>1)是增函数,随着x的增大,y=ax(a>1)的增长速度越来越快,形象地称为“指数爆炸”.
反思感悟
下表是函数值y随自变量x变化的一组数据,由此判断它最符合的函数模型是
A.一次函数
B.二次函数
C.指数型函数
D.对数型函数
跟踪训练1
x 3 4 5 6 7
y 3.38 5.06 7.59 11.39 67.09
√
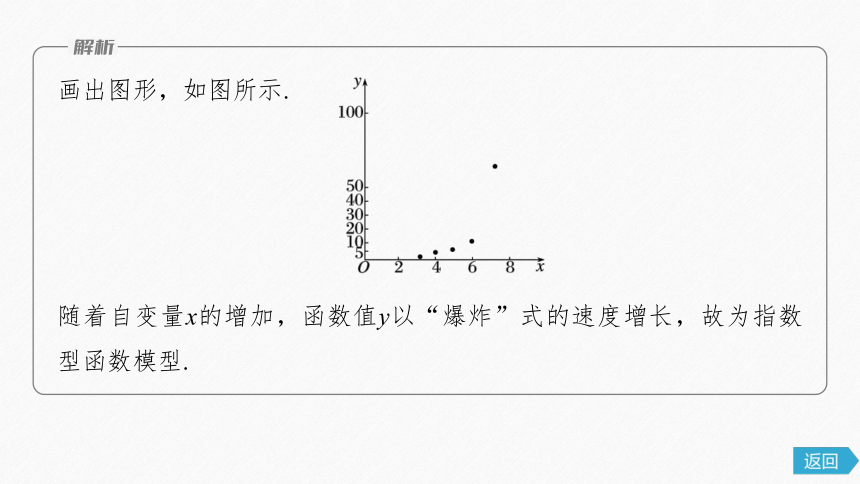
画出图形,如图所示.
随着自变量x的增加,函数值y以“爆炸”式的速度增长,故为指数型函数模型.
二
函数模型增长差异的比较(图象)
问题 把一次函数y=2x,对数函数y=lg x和指数函数y=2x的图象画到同一坐标系下,并比较它们的增长差异.
提示
一次函数y=2x匀速增长,指数函数y=2x增长越来越快,对数函数y=lg x增长最慢.
知识梳理
指数函数与对数函数、幂函数的增长趋势比较
函数 性质 y=ax(a>1) y=logax(a>1) y=xα(α>0)
在(0,+∞)上的增减性 _______ _______ _______
图象的变化 随x的增大逐渐变“陡” 随x的增大逐渐趋于稳定 随α值的不同而不同
增长速度 ax的增长 xα的增长,xα的增长 logax的增长 增长后果 当x足够大时,有 (a>1) 增函数
增函数
增函数
快于
快于
ax>xα>logax
(1)下列函数中,增长速度最快的是
A.y=2 023x
B.y=x2 023
C.y=log2 023x
D.y=2 023x
例2
√
(2)某生物研究者于元旦在湖中放入一些凤眼莲(其覆盖面积为k),这些凤眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲的覆盖面积为24 m2,三月底测得凤眼莲的覆盖面积为36 m2,凤眼莲的覆盖面积y(单位:m2)与月份x(单位:月)之间的关系有两个函数模型y=kax(k>0,a>1)与
(p>0,k>0)可供选择.
试判断哪个函数模型更合适并求出该模型的解析式.
由题设可知,两个函数y=kax(k>0,a>1), (p>0,k>0)在(0,+∞)上均为增函数,
随着x的增大,函数y=kax(k>0,a>1)的值增加得越来越快,
而函数 (p>0,k>0)的值增加得越来越慢,
由于凤眼莲在湖中的蔓延速度越来越快,故而函数模型y=kax(k>0,a>1)满足要求.
指数函数、对数函数和幂函数增长差异的判断方法
(1)根据函数的变化量的情况对函数增长模型进行判断.
(2)根据图象判断增长型的指数函数、对数函数和幂函数时,通常是观察函数图象上升的快慢,即随着自变量的增大,图象最“陡”的函数是指数函数;图象趋于平缓的函数是对数函数.
反思感悟
函数f(x)=2x和g(x)=x3的图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1(1)请指出图中曲线C1,C2分别对应的函数;
跟踪训练2
C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.
(2)结合函数图象,判断f(6),g(6),f(2 022),g(2 022)的大小.
因为f(1)>g(1),f(2)g(10),
所以1x2,
从图象上可以看出,
当x1所以f(6)当x>x2时,f(x)>g(x),
所以f(2 022)>g(2 022).
又因为g(2 022)>g(6),
所以f(2 022)>g(2 022)>g(6)>f(6).
课堂
小结
1.知识清单:
(1)指数增长.
(2)幂函数、指数函数、对数函数增长趋势的比较.
2.方法归纳:数形结合法.
3.常见误区:函数值大小关系比较时没有注意所给区间.
随堂演练
1.下列函数中,随着x的增长,增长速度最快的是
A.y=50x B.y=1 000x
1
2
3
4
指数函数y=ax,在a>1时呈爆炸式增长,而且a越大,增长速度越快.
√
1
2
3
4
2.某公司为了适应市场需求对产品结构作了重大调整,调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润y与时间x的关系,可选用
A.一次函数 B.幂函数
C.指数型函数 D.对数型函数
√
初期增长迅速,后来增长越来越慢,可用对数型函数模型来反映y与x的关系.
1
2
3
4
3.如图所示给出了红豆生长时间t(月)与枝数y(枝)的散点图,那么最能拟合诗句“红豆生南国,春来发几枝”所提到的红豆生长时间与枝数的关系的函数模型为
A.指数函数:y=2t
B.对数函数:y=log2t
C.幂函数:y=t3
D.二次函数:y=2t2
√
由散点图可知,与指数函数拟合的最贴切.
1
2
3
4
4.若a>1,n>0,那么当x足够大时,ax,xn,logax的大小关系是______________.
ax>xn>logax
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1.某研究小组在一项实验中获得一组关于y,t的数据,将其整理得到如图所示的图形.下列函数中最能近似刻画y与t之间关系的是
A.y=2t
B.y=2t2
C.y=t3
D.y=log2t
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.当2<x<4时,2x,x2,log2x的大小关系是
A.2x>x2>log2x B.x2>2x>log2x
C.2x>log2x>x2 D.x2>log2x>2x
√
方法一 在同一平面直角坐标系中分别画出函数y=log2x,y=x2,y=2x的图象(图略),在区间(2,4)上从上往下依次是y=x2,y=2x,y=log2x的图象,所以x2>2x>log2x.
方法二 比较三个函数值的大小,作为选择题,可以采用特殊值代入法.可取x=3,经检验易知x2>2x>log2x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.某地区植被被破坏,土地沙漠化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x(年)的函数关系较为近似的是
将x=1,2,3,y=0.2,0.4,0.76分别代入验算.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.有一组实验数据如下表所示:
x 1 2 3 4 5
y 1.5 5.9 13.4 24.1 37
下列所给函数模型较适合的是
A.y=logax(a>1) B.y=ax+b(a>1)
C.y=ax2+b(a>0) D.y=logax+b(a>1)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
通过所给数据可知y随x增大,其增长速度越来越快,而A,D中的函数增长速度越来越慢,而B中的函数增长速度保持不变.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.某新款电视投放市场后第一个月销售了100台,第二个月销售了200台,第三个月销售了400台,第四个月销售了790台,则下列函数模型中能较好地反映销量y与投放市场的月数x(1≤x≤4,x∈N*)之间关系的是
A.y=100x B.y=50x2-50x+100
C.y=50×2x D.y=100x
√
将数据代入各函数中,易知指数型函数能较好地与题中的数据相对应.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,f2(x)=x2,f3(x)=x,f4(x)=log2(x+1),以下说法正确的是
A.当x>1时,乙走在最前面
B.当01时,丁走在最后面
C.丙不可能走在最前面,也不可能走在最后面
D.如果它们一直运动下去,最终走在最前面的是甲
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
f1(x)=2x-1,f2(x)=x2,f3(x)=x,f4(x)=log2(x+1)相应的函数模型分别是指数型函数,二次函数,一次函数和对数型函数模型.当x=5时,f1(5)=31,f2(5)=25,f1(5)>f2(5),A不正确;
根据四种函数的变化特点,对数型函数的变化是先快后慢,当x=1时甲、乙、丙、丁四个物体又重合,从而可知当01时,丁走在最后面,B正确;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
指数函数变化是先慢后快,当运动的时间足够长,最前面的一定是按照指数型函数运动的物体,即一定是甲物体,D正确;
结合对数型和指数型函数的图象变化情况,可知丙不可能走在最前面,也不可能走在最后面,C正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.物价上涨是当前的热点话题,特别是肉价,我国某部门为尽快实现稳定肉价,提出四种绿色运输方案.据预测,这四种方案均能在规定的时间T内完成预测的运输任务Q0,各种方案的运输总量Q与时间t的函数关系如图所示,在这四种方案中,运输效率(单位时间的运输量)逐步提高的是______.
Q的值随t的变化越来越快,即运输效率在逐步提高,只有②吻合.
②
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.如图所示,折线是某电信局规定打长途电话所需要付的电话费y(元)与通话时间t(分钟)之间的函数关系图象,根据图象填空:
(1)通话5分钟,需付电话费______元;
由图象知,当t=5时,y=6,需付电话费6元.
6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)如果t≥3,则电话费y(元)与通话时间t(分钟)之间的函数关系式为______________.
y=1.2t(t≥3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当t≥3时,y关于t的图象是一条直线,
且经过(3,3.6)和(5,6)两点,
故设函数关系式为y=kt+b,
故电话费y(元)与通话时间t(分钟)之间的函数关系式为y=1.2t(t≥3).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.函数f(x)=lg x,g(x)=0.3x-1的图象如图所示.
C1对应的函数为g(x)=0.3x-1,C2对应的函数为f(x)=lg x.
(1)试根据函数的增长差异指出曲线C1,C2分别对应的函数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).
当0f(x);
当x1g(x);
当x>x2时,g(x)>f(x);
当x=x1或x=x2时,f(x)=g(x).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知某种药物在血液中以每小时20%的比例衰减,现给某病人静脉注射了该药物2 500 mg,设经过x个小时后,药物在病人血液中的量为y mg.
(1)求y与x的关系式;
由题意知,该种药物在血液中以每小时20%的比例衰减,给某病人注射了该药物2 500 mg,经过x个小时后,药物在病人血液中的量为y=2 500×(1-20%)x=2 500×0.8x(mg),即y与x的关系式为y=2 500 ×0.8x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当该药物在病人血液中的量保持在1 500 mg以上时,才有疗效;而低于500 mg时,病人就有危险.则要使病人没有危险,再次注射该药物的时间不能超过多少小时(精确到0.1)
(参考数据:0.20.3≈0.6,0.82.3≈0.6,0.87.2≈0.2,0.89.9≈0.1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当该药物在病人血液中的量保持在1 500 mg以上时,才有疗效,而低于500 mg时,病人就有危险,
∴令2 500×0.8x≥500,即0.8x≥0.2.
∵0.87.2≈0.2,y=0.8x是减函数,
∴x≤7.2,
∴要使病人没有危险,再次注射该药物的时间不能超过7.2小时.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.下列对函数 g(x)= 与 在区间(0,+∞)上的递减情况说法正确的是
A.f(x)递减速度越来越慢,g(x)递减速度越来越快,h(x)递减速度越来越慢
B.f(x)递减速度越来越快,g(x)递减速度越来越慢,h(x)递减速度越来越快
C.f(x)递减速度越来越慢,g(x)递减速度越来越慢,h(x)递减速度越来越慢
D.f(x)递减速度越来越快,g(x)递减速度越来越快,h(x)递减速度越来越快
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
观察函数 g(x)= 与 在区
间(0,+∞)上的图象(如图)可知:函数f(x)的图象
在区间(0,1)上递减较快,但递减速度逐渐变慢;在
区间(1,+∞)上,递减较慢,且越来越慢;同样,函数g(x)的图象在区间(0,+∞)上,递减较慢,且递减速度越来越慢;函数h(x)的图象在区间(0,1)上递减较快,但递减速度逐渐变慢;在区间(1,+∞)上,递减较慢,且越来越慢.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.某种纯净水制造厂在净化水过程中,每增加一次过滤可减少水中杂质的20%,要使水中杂质减少到原来的10%以下,则至少需过滤的次数为(参考数据:lg 2≈0.301 0)
A.10 B.11 C.12 D.13
√
设过滤次数为x,原有杂质为a,
则a(1-20%)x<a·10%,
即x>10.31,即至少需要过滤11次.
13.安徽怀远石榴(Punicagranatum)自古就有“九州之奇树,天下之名果”的美称,今年又喜获丰收.某中学数学兴趣小组进行社会调查,了解到某石榴合作社为了实现100万元利润目标,准备制定激励销售人员的奖励方案:在销售利润超过6万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过3万元,同时奖金不能超过利润的20%.同学们利用函数知识设计了如下函数模型,其中符合合作社要求的是
(参考数据:1.015100≈4.432,lg 11≈1.041)
A.y=0.04x B.y=1.015x-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于函数y=0.04x,当x=100时,y=4>3,不符合题意;
对于函数y=1.015x-1,当x=100时,y=3.432>3,不符合题意;
对于函数y=log11(3x-10),满足当x∈(6,100]时,函数为增函数,
且y≤log11(3×100-10)=log112901
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.如图,与函数y=2x,y=5x, ,y=log0.5x,
y=log0.3x相对应的图象依次为_______________.
(只填序号)
(1)(2)分别为y=5x和y=2x的图象;
(3)为 的图象;
(4)(5)分别为y=log0.3x和y=log0.5x的图象.
(2)(1)(3)(5)(4)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.生活经验告诉我们,当水注入容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在图中请选择与容器相匹配的图象,A对应______;B对应______;C对应______;D对应______.
(4) (1) (3) (2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A容器下粗上细,水高度的变化先慢后快,故与(4)对应;
B容器为球形,水高度变化为快—慢—快,应与(1)对应;
C,D容器都是柱形的,水高度的变化速度都应是直线型,
但C容器细,D容器粗,故水高度的变化为:C容器快,与(3)对应,D容器慢,与(2)对应.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.假设有一套住房从2012年的20万元上涨到2022年的40万元.下表给出了两种价格增长方式,其中P1是按直线上升的房价,P2是按指数增长的房价,t是2012年以来经过的年数.
t 0 5 10 15 20
P1/万元 20 40
P2/万元 20 40
(1)求函数P1=f(t)的解析式;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为P1是按直线上升的房价,
设f(t)=kt+b(k≠0),t≥0,
由f(0)=k·0+b=20,
f(10)=k·10+b=40,
可得k=2,b=20,
即P1=2t+20,t≥0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求函数P2=g(t)的解析式;
因为P2是按指数增长的房价,
设g(t)=a0at(a>0且a≠1),t≥0,
由g(0)=a0a0=20,g(10)=a0a10=40,
可得a0=20,
即P2=20× ,t≥0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)完成上表空格中的数据,并在同一直角坐标系中画出两个函数的图象,然后比较两种价格增长方式的差异.
t 0 5 10 15 20
P1/万元 20 40
P2/万元 20 40
由(1)和(2)知,当t=5时,
当t=20时,P1=60,P2=80,
则表格如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则图象为
根据表格和图象可知,房价按函数P1=f(t)呈直线上升,每年的增加量相同,保持相同的增长速度;按函数P2=g(t)呈指数增长,每年的增加量越来越大,开始增长慢,然后会越来越快,但保持相同的增长比例.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.2.1 几个函数模型的比较
第8章 §8.2 函数与数学模型
学习目标
1.了解指数爆炸、对数增长等含义.
2.借助信息技术,作出函数图象,比较指数函数、对数函数以及幂函数的增长差异.
3.了解不同函数模型的“变化趋势”,加深对自然现象的理解.
导语
如果你现在手里有一笔资金可以用于投资,现在有三种投资方案供你选择,这三种方案的回报是这样的:方案一:每天回报40元;方案二:第一天回报10元,以后每天比前一天多回报10元;方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.请问,你会选择哪种投资方案?为了解决这个问题,让我们一起开始今天的探究吧!
一、指数爆炸(求值)
二、函数模型增长差异的比较(图象)
课时对点练
随堂演练
内容索引
指数爆炸(求值)
一
知识梳理
指数变化
当a>1时,指数函数y=ax随着x的增大而 ,且增大的速度越来越 ,呈“爆炸”的趋势,因此“指数增长”可以用“指数爆炸”来形容.
当0
快
减小
0
四个自变量y1,y2,y3,y4随变量x变化的数据如下表:
例1
x 1 5 10 15 20 25 30
y1 2 26 101 226 401 626 901
y2 2 32 1 024 32 768 1.05×106 3.36×107 1.07×109
y3 2 10 20 30 40 50 60
y4 2 4.322 5.322 5.907 6.322 6.644 6.907
则关于x呈指数型函数变化的变量是_____.
y2
以爆炸式增长的变量呈指数函数变化.从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,且都是越来越大,但是增长速度不同,其中变量y2的增长速度最快,画出它们的图象(图略),可知变量y2关于x呈指数型函数变化.
指数函数增长的特点
指数函数y=ax(a>1)是增函数,随着x的增大,y=ax(a>1)的增长速度越来越快,形象地称为“指数爆炸”.
反思感悟
下表是函数值y随自变量x变化的一组数据,由此判断它最符合的函数模型是
A.一次函数
B.二次函数
C.指数型函数
D.对数型函数
跟踪训练1
x 3 4 5 6 7
y 3.38 5.06 7.59 11.39 67.09
√
画出图形,如图所示.
随着自变量x的增加,函数值y以“爆炸”式的速度增长,故为指数型函数模型.
二
函数模型增长差异的比较(图象)
问题 把一次函数y=2x,对数函数y=lg x和指数函数y=2x的图象画到同一坐标系下,并比较它们的增长差异.
提示
一次函数y=2x匀速增长,指数函数y=2x增长越来越快,对数函数y=lg x增长最慢.
知识梳理
指数函数与对数函数、幂函数的增长趋势比较
函数 性质 y=ax(a>1) y=logax(a>1) y=xα(α>0)
在(0,+∞)上的增减性 _______ _______ _______
图象的变化 随x的增大逐渐变“陡” 随x的增大逐渐趋于稳定 随α值的不同而不同
增长速度 ax的增长 xα的增长,xα的增长 logax的增长 增长后果 当x足够大时,有 (a>1) 增函数
增函数
增函数
快于
快于
ax>xα>logax
(1)下列函数中,增长速度最快的是
A.y=2 023x
B.y=x2 023
C.y=log2 023x
D.y=2 023x
例2
√
(2)某生物研究者于元旦在湖中放入一些凤眼莲(其覆盖面积为k),这些凤眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲的覆盖面积为24 m2,三月底测得凤眼莲的覆盖面积为36 m2,凤眼莲的覆盖面积y(单位:m2)与月份x(单位:月)之间的关系有两个函数模型y=kax(k>0,a>1)与
(p>0,k>0)可供选择.
试判断哪个函数模型更合适并求出该模型的解析式.
由题设可知,两个函数y=kax(k>0,a>1), (p>0,k>0)在(0,+∞)上均为增函数,
随着x的增大,函数y=kax(k>0,a>1)的值增加得越来越快,
而函数 (p>0,k>0)的值增加得越来越慢,
由于凤眼莲在湖中的蔓延速度越来越快,故而函数模型y=kax(k>0,a>1)满足要求.
指数函数、对数函数和幂函数增长差异的判断方法
(1)根据函数的变化量的情况对函数增长模型进行判断.
(2)根据图象判断增长型的指数函数、对数函数和幂函数时,通常是观察函数图象上升的快慢,即随着自变量的增大,图象最“陡”的函数是指数函数;图象趋于平缓的函数是对数函数.
反思感悟
函数f(x)=2x和g(x)=x3的图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1
跟踪训练2
C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.
(2)结合函数图象,判断f(6),g(6),f(2 022),g(2 022)的大小.
因为f(1)>g(1),f(2)
所以1
从图象上可以看出,
当x1
所以f(2 022)>g(2 022).
又因为g(2 022)>g(6),
所以f(2 022)>g(2 022)>g(6)>f(6).
课堂
小结
1.知识清单:
(1)指数增长.
(2)幂函数、指数函数、对数函数增长趋势的比较.
2.方法归纳:数形结合法.
3.常见误区:函数值大小关系比较时没有注意所给区间.
随堂演练
1.下列函数中,随着x的增长,增长速度最快的是
A.y=50x B.y=1 000x
1
2
3
4
指数函数y=ax,在a>1时呈爆炸式增长,而且a越大,增长速度越快.
√
1
2
3
4
2.某公司为了适应市场需求对产品结构作了重大调整,调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润y与时间x的关系,可选用
A.一次函数 B.幂函数
C.指数型函数 D.对数型函数
√
初期增长迅速,后来增长越来越慢,可用对数型函数模型来反映y与x的关系.
1
2
3
4
3.如图所示给出了红豆生长时间t(月)与枝数y(枝)的散点图,那么最能拟合诗句“红豆生南国,春来发几枝”所提到的红豆生长时间与枝数的关系的函数模型为
A.指数函数:y=2t
B.对数函数:y=log2t
C.幂函数:y=t3
D.二次函数:y=2t2
√
由散点图可知,与指数函数拟合的最贴切.
1
2
3
4
4.若a>1,n>0,那么当x足够大时,ax,xn,logax的大小关系是______________.
ax>xn>logax
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1.某研究小组在一项实验中获得一组关于y,t的数据,将其整理得到如图所示的图形.下列函数中最能近似刻画y与t之间关系的是
A.y=2t
B.y=2t2
C.y=t3
D.y=log2t
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.当2<x<4时,2x,x2,log2x的大小关系是
A.2x>x2>log2x B.x2>2x>log2x
C.2x>log2x>x2 D.x2>log2x>2x
√
方法一 在同一平面直角坐标系中分别画出函数y=log2x,y=x2,y=2x的图象(图略),在区间(2,4)上从上往下依次是y=x2,y=2x,y=log2x的图象,所以x2>2x>log2x.
方法二 比较三个函数值的大小,作为选择题,可以采用特殊值代入法.可取x=3,经检验易知x2>2x>log2x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.某地区植被被破坏,土地沙漠化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x(年)的函数关系较为近似的是
将x=1,2,3,y=0.2,0.4,0.76分别代入验算.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.有一组实验数据如下表所示:
x 1 2 3 4 5
y 1.5 5.9 13.4 24.1 37
下列所给函数模型较适合的是
A.y=logax(a>1) B.y=ax+b(a>1)
C.y=ax2+b(a>0) D.y=logax+b(a>1)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
通过所给数据可知y随x增大,其增长速度越来越快,而A,D中的函数增长速度越来越慢,而B中的函数增长速度保持不变.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.某新款电视投放市场后第一个月销售了100台,第二个月销售了200台,第三个月销售了400台,第四个月销售了790台,则下列函数模型中能较好地反映销量y与投放市场的月数x(1≤x≤4,x∈N*)之间关系的是
A.y=100x B.y=50x2-50x+100
C.y=50×2x D.y=100x
√
将数据代入各函数中,易知指数型函数能较好地与题中的数据相对应.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,f2(x)=x2,f3(x)=x,f4(x)=log2(x+1),以下说法正确的是
A.当x>1时,乙走在最前面
B.当0
C.丙不可能走在最前面,也不可能走在最后面
D.如果它们一直运动下去,最终走在最前面的是甲
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
f1(x)=2x-1,f2(x)=x2,f3(x)=x,f4(x)=log2(x+1)相应的函数模型分别是指数型函数,二次函数,一次函数和对数型函数模型.当x=5时,f1(5)=31,f2(5)=25,f1(5)>f2(5),A不正确;
根据四种函数的变化特点,对数型函数的变化是先快后慢,当x=1时甲、乙、丙、丁四个物体又重合,从而可知当0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
指数函数变化是先慢后快,当运动的时间足够长,最前面的一定是按照指数型函数运动的物体,即一定是甲物体,D正确;
结合对数型和指数型函数的图象变化情况,可知丙不可能走在最前面,也不可能走在最后面,C正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.物价上涨是当前的热点话题,特别是肉价,我国某部门为尽快实现稳定肉价,提出四种绿色运输方案.据预测,这四种方案均能在规定的时间T内完成预测的运输任务Q0,各种方案的运输总量Q与时间t的函数关系如图所示,在这四种方案中,运输效率(单位时间的运输量)逐步提高的是______.
Q的值随t的变化越来越快,即运输效率在逐步提高,只有②吻合.
②
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.如图所示,折线是某电信局规定打长途电话所需要付的电话费y(元)与通话时间t(分钟)之间的函数关系图象,根据图象填空:
(1)通话5分钟,需付电话费______元;
由图象知,当t=5时,y=6,需付电话费6元.
6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)如果t≥3,则电话费y(元)与通话时间t(分钟)之间的函数关系式为______________.
y=1.2t(t≥3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当t≥3时,y关于t的图象是一条直线,
且经过(3,3.6)和(5,6)两点,
故设函数关系式为y=kt+b,
故电话费y(元)与通话时间t(分钟)之间的函数关系式为y=1.2t(t≥3).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.函数f(x)=lg x,g(x)=0.3x-1的图象如图所示.
C1对应的函数为g(x)=0.3x-1,C2对应的函数为f(x)=lg x.
(1)试根据函数的增长差异指出曲线C1,C2分别对应的函数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).
当0
当x1
当x>x2时,g(x)>f(x);
当x=x1或x=x2时,f(x)=g(x).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知某种药物在血液中以每小时20%的比例衰减,现给某病人静脉注射了该药物2 500 mg,设经过x个小时后,药物在病人血液中的量为y mg.
(1)求y与x的关系式;
由题意知,该种药物在血液中以每小时20%的比例衰减,给某病人注射了该药物2 500 mg,经过x个小时后,药物在病人血液中的量为y=2 500×(1-20%)x=2 500×0.8x(mg),即y与x的关系式为y=2 500 ×0.8x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当该药物在病人血液中的量保持在1 500 mg以上时,才有疗效;而低于500 mg时,病人就有危险.则要使病人没有危险,再次注射该药物的时间不能超过多少小时(精确到0.1)
(参考数据:0.20.3≈0.6,0.82.3≈0.6,0.87.2≈0.2,0.89.9≈0.1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当该药物在病人血液中的量保持在1 500 mg以上时,才有疗效,而低于500 mg时,病人就有危险,
∴令2 500×0.8x≥500,即0.8x≥0.2.
∵0.87.2≈0.2,y=0.8x是减函数,
∴x≤7.2,
∴要使病人没有危险,再次注射该药物的时间不能超过7.2小时.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.下列对函数 g(x)= 与 在区间(0,+∞)上的递减情况说法正确的是
A.f(x)递减速度越来越慢,g(x)递减速度越来越快,h(x)递减速度越来越慢
B.f(x)递减速度越来越快,g(x)递减速度越来越慢,h(x)递减速度越来越快
C.f(x)递减速度越来越慢,g(x)递减速度越来越慢,h(x)递减速度越来越慢
D.f(x)递减速度越来越快,g(x)递减速度越来越快,h(x)递减速度越来越快
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
观察函数 g(x)= 与 在区
间(0,+∞)上的图象(如图)可知:函数f(x)的图象
在区间(0,1)上递减较快,但递减速度逐渐变慢;在
区间(1,+∞)上,递减较慢,且越来越慢;同样,函数g(x)的图象在区间(0,+∞)上,递减较慢,且递减速度越来越慢;函数h(x)的图象在区间(0,1)上递减较快,但递减速度逐渐变慢;在区间(1,+∞)上,递减较慢,且越来越慢.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.某种纯净水制造厂在净化水过程中,每增加一次过滤可减少水中杂质的20%,要使水中杂质减少到原来的10%以下,则至少需过滤的次数为(参考数据:lg 2≈0.301 0)
A.10 B.11 C.12 D.13
√
设过滤次数为x,原有杂质为a,
则a(1-20%)x<a·10%,
即x>10.31,即至少需要过滤11次.
13.安徽怀远石榴(Punicagranatum)自古就有“九州之奇树,天下之名果”的美称,今年又喜获丰收.某中学数学兴趣小组进行社会调查,了解到某石榴合作社为了实现100万元利润目标,准备制定激励销售人员的奖励方案:在销售利润超过6万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过3万元,同时奖金不能超过利润的20%.同学们利用函数知识设计了如下函数模型,其中符合合作社要求的是
(参考数据:1.015100≈4.432,lg 11≈1.041)
A.y=0.04x B.y=1.015x-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于函数y=0.04x,当x=100时,y=4>3,不符合题意;
对于函数y=1.015x-1,当x=100时,y=3.432>3,不符合题意;
对于函数y=log11(3x-10),满足当x∈(6,100]时,函数为增函数,
且y≤log11(3×100-10)=log11290
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.如图,与函数y=2x,y=5x, ,y=log0.5x,
y=log0.3x相对应的图象依次为_______________.
(只填序号)
(1)(2)分别为y=5x和y=2x的图象;
(3)为 的图象;
(4)(5)分别为y=log0.3x和y=log0.5x的图象.
(2)(1)(3)(5)(4)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.生活经验告诉我们,当水注入容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在图中请选择与容器相匹配的图象,A对应______;B对应______;C对应______;D对应______.
(4) (1) (3) (2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A容器下粗上细,水高度的变化先慢后快,故与(4)对应;
B容器为球形,水高度变化为快—慢—快,应与(1)对应;
C,D容器都是柱形的,水高度的变化速度都应是直线型,
但C容器细,D容器粗,故水高度的变化为:C容器快,与(3)对应,D容器慢,与(2)对应.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.假设有一套住房从2012年的20万元上涨到2022年的40万元.下表给出了两种价格增长方式,其中P1是按直线上升的房价,P2是按指数增长的房价,t是2012年以来经过的年数.
t 0 5 10 15 20
P1/万元 20 40
P2/万元 20 40
(1)求函数P1=f(t)的解析式;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为P1是按直线上升的房价,
设f(t)=kt+b(k≠0),t≥0,
由f(0)=k·0+b=20,
f(10)=k·10+b=40,
可得k=2,b=20,
即P1=2t+20,t≥0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求函数P2=g(t)的解析式;
因为P2是按指数增长的房价,
设g(t)=a0at(a>0且a≠1),t≥0,
由g(0)=a0a0=20,g(10)=a0a10=40,
可得a0=20,
即P2=20× ,t≥0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)完成上表空格中的数据,并在同一直角坐标系中画出两个函数的图象,然后比较两种价格增长方式的差异.
t 0 5 10 15 20
P1/万元 20 40
P2/万元 20 40
由(1)和(2)知,当t=5时,
当t=20时,P1=60,P2=80,
则表格如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则图象为
根据表格和图象可知,房价按函数P1=f(t)呈直线上升,每年的增加量相同,保持相同的增长速度;按函数P2=g(t)呈指数增长,每年的增加量越来越大,开始增长慢,然后会越来越快,但保持相同的增长比例.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
