27.2 二次函数的图象与性质(7课时课件)
文档属性
| 名称 | 27.2 二次函数的图象与性质(7课时课件) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-19 10:27:10 | ||
图片预览








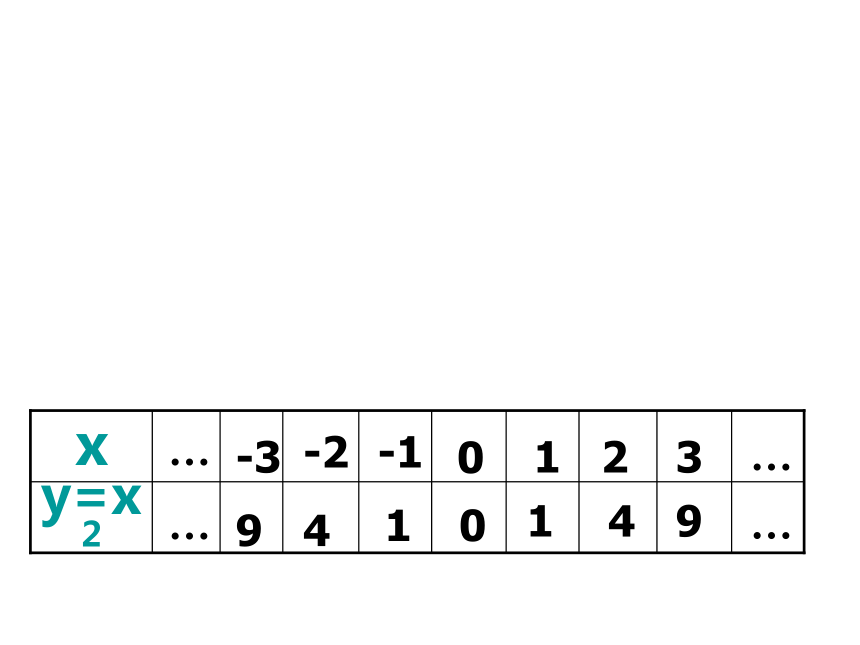
文档简介
课件106张PPT。华东师大版
九年级(下)数学教学课件27.2 二次函数的图象与性质华东师大版九年级(下册)(第1课时)函数y=ax2+bx+c (a,b,c是常数,a≠ 0) 叫做x的二次函数.什么叫二次函数?我们学过用什么方法画函数
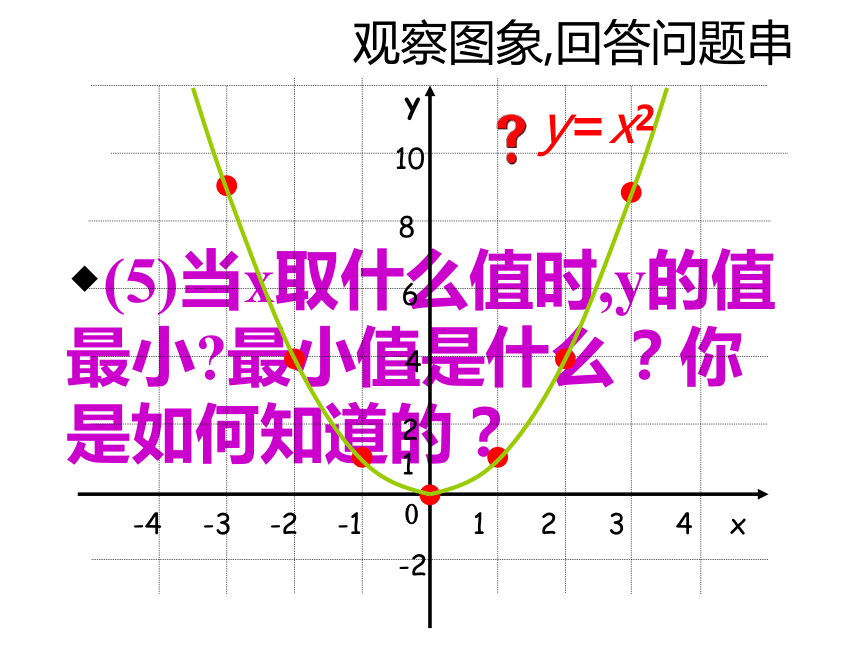
的图象?主要有哪些步骤?观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表:用描点法画二次函数y=x2的图象0123…0149…描点,连线y=x2观察图象,回答问题串(1)你能描述图象的形状吗?与同伴进行交流.(2)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流.观察图象,回答问题串(3)图象 与x轴有交点吗?如果有,交点坐标是什么?(4)在对称轴左侧,随着x值的增大,y 的值如何变化?在对称轴右侧呢?观察图象,回答问题串(5)当x取什么值时,y的值最小?最小值是什么?你是如何知道的?这条抛物线关于
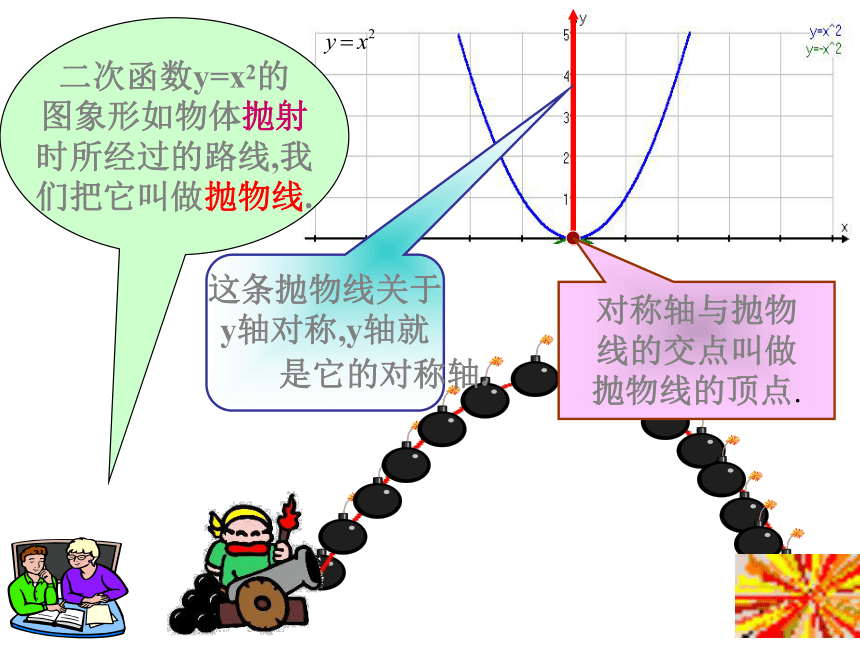
y轴对称,y轴就
是它的对称轴. 对称轴与抛物
线的交点叫做
抛物线的顶点.二次函数y=x2的
图象形如物体抛射
时所经过的路线,我
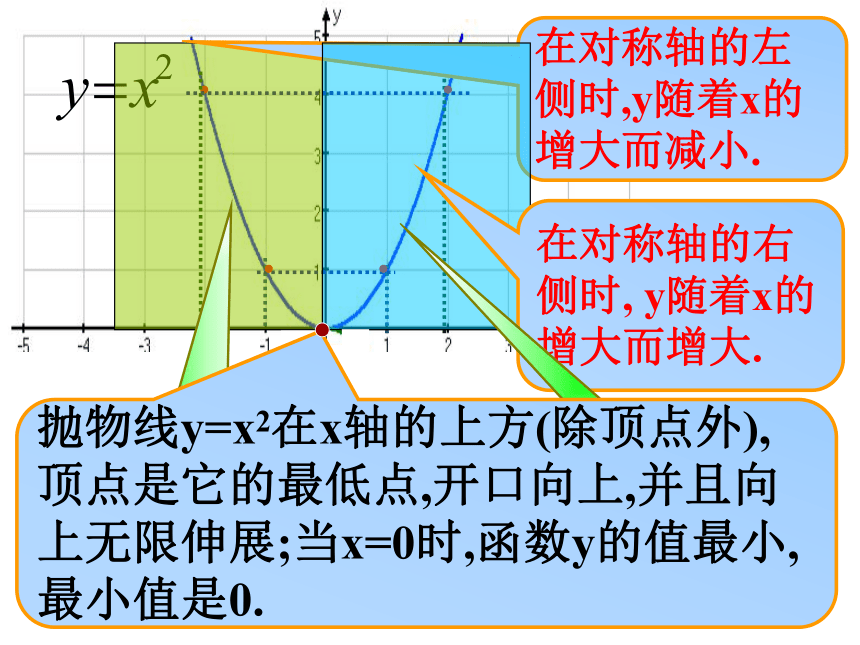
们把它叫做抛物线.在对称轴的左
侧时,y随着x的
增大而减小. 在对称轴的右
侧时, y随着x的
增大而增大. 抛物线y=x2在x轴的上方(除顶点外),
顶点是它的最低点,开口向上,并且向
上无限伸展;当x=0时,函数y的值最小,
最小值是0.(1)二次函数y=-x2的图象是什么形状?(2)它与二次函数y=x2的图象有什么关系?你能根据表格中的数据作出猜想吗?xy0-4-3-2-11234-10-8-6-4-22-1描点,连线y=-x2这条抛物线关于
y轴对称,y轴就
是它的对称轴. 对称轴与抛物
线的交点叫做
抛物线的顶点.yy在对称轴的左侧
时,y随着x的增大
而增大. 在对称轴的右侧
时, y随着x的增大
而减小. y抛物线y= -x2在x轴的下方(除顶点外),
顶点是它的最高点,开口向下,并且向下
无限伸展;当x=0时,函数y的值最大,
最大值是0.抛物线顶点坐标对称轴位置开口方向增减性最值y=x2y= -x2(0,0)(0,0)y轴y轴在x轴的上方(除顶点外)在x轴的下方( 除顶点外)向上向下当x=0时,最小值为0.当x=0时,最大值为0.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 函数y=ax2(a≠0)的图象和性质:y=x2y=-x21.顶点坐标与对称轴2.位置与开口方向3.增减性与最值1.抛物线y=ax2的顶点是原点,对称轴是y轴.2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.二次函数y=ax2的性质1.已知抛物线y=ax2经过点A(-2,-8)
(1)求此抛物线的函数解析式;
(2)判断点B(-1,-4)是否在此抛物线上;
(3)求出此抛物线上纵坐标为-6的点的坐标;
(4)若点(m,n)在此抛物线上,那么点
(-m,n)是否在此抛物线上?点(m,-n)呢?2.填空:
(1)抛物线y=2x2的顶点坐标是_____;
对称轴是______;在___________ 侧,
y随着x的增大而增大;在_________侧,
y随着x的增大而减小;当x= 时,函数y的值最小,最小值是 ;抛物线y=2x2在x轴的 方(除顶点外).(0,0)y轴对称轴的左0对称轴的右0上(2)抛物线 在x轴的 方(除顶点外),
当x_____时,y随着x的增大而增大;
当x_____时,y随着x的,增大而减小
当x=0时,函数y的值最大,最大值是_____,
当x 0时,y<0.下0<0>0回味无穷2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;
在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;
在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.1.抛物线y=ax2的顶点是原点,对称轴是y轴.由二次函数y=x2和y=-x2知:27.2 二次函数的图象与性质(第2课时)华东师大版九年级(下册)比较二次函数 y=x2 和 y= –x2 图象的异同:二次函数 y=2x2 的图象是什么形状?它与二次函数 y=x2 的图象有什么相同和不同?(1)二次函数 y=2x2+1 的图象与二次函数 y=2x2 的图象有什么关系?(2)二次函数 y=3x2-1 的图象与二次函数 y=3x2 的图象有什么关系?y在同一直角坐标系中画出函数
的图像试说出函数y=ax2+k(a、k是常数,a≠0)的图象的开口方向、对称轴和顶点坐标,并填写下表. 向上向下y轴y轴(0,k)(0,k)练习
1.把抛物线 向下平移2个单位,可以得到抛物线 ,在向上平移5个单位,可以得到抛物线 ;
2.对于函数y= –x2+1,当x 时,函数值y随x的增大而增大;当x 时,函数值y随x的增大而减小;当x 时,函数取得最 值,为 。<0>0=0大03.函数y=3x2+5与y=3x2的图象的不同之处是( )
A.对称轴 B.开口方向
C.顶点 D.形状
4.已知抛物线y=2x2-1上有两点(x1,y1 ) ,(x1,y1 )且x1<x2<0,则y1 y2(填“<”或“>”)C<5.已知一个二次函数图像的顶点在y轴上,并且离原点1个单位,图像经过点(–1,0),求该二次函数解析式。
6.已知抛物线 ,把它向下平移,得到的抛物线与x轴交于A、B两点,与y轴交于C点,若⊿ABC是直角三角形,那么原抛物线应向下平移几个单位?27.2二次函数的图象与性质(第3课时)华东师大版九年级(下册)1.抛物线y=ax2的顶点是原点,对称轴是y轴.2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外), 它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.二次函数y=ax2的性质在同一个直角坐标系里画出函数 与 的图象.xy0-8-6-4-2246820161284-2描点,连线1012-10-122观察这两个函数的图象,
它们有什么关系?xy0-8-6-4-2246820161284-2描点,连线1012-10-1222xyO函数y= (x-2)2的图象与y= x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么? 二次项系数
相同 a>0,
开口都向上,两个二次函数的图象
形状相同,可以看作是
抛物线y= x2整体
沿x轴向右平移了2
个单位2xyO函数y= (x-2)2的图象与y= x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么? 顶点坐标
是点(2,0).图象是轴对称图形
对称轴是平行于
y轴的直线:x=2.2xyOx取哪些值时,函数y= (x-1)2的值随x值的增大而减小?x取哪些值时,函数y= (x-1)2的值随x的增大而增大? 在对称轴(直线:x=2)
左侧(即x<2时), y的值
随x的增大而减小,.在对称轴(直线:x=2)
右侧(即x>2时), y的值
随x的增大而增大,.顶点是最低点,函数
有最小值.当x=2时,
最小值是0..想一想, 这个函数的图象和性质会是什么样? 在同一个直角坐标系里画出 函数 和 的图象 xy0-8-6-4-2246820161284-2描点,连线1012-10-122观察函数 与 的
图象,它们有什么关系?xy0-8-6-4-2246820161284-2描点,连线1012-10-122函数 与 的
图象有什么关系?说出它
的顶点坐标和对称轴直线x=-2函数 的图象可以看成由
的图象向_____平移___个单位得到,它们的形状和开口大小相同函数 的图象可以看成由
的图象向____平移___个单位得到,它们的形状和开口大小相同这里的平移方向有什么规律?右左22函数y=a(x-h)2(a≠0)的图象和性质1.函数y=a(x-h)2(a≠0)的图象可
由函数y=ax2的图象平移得到.
当h>0 时,向___平移___个单位
当h<0 时,向___平移____个单位
对称轴为:_________.顶点为____h|h|右左直线x=h(h,0)2.当a>0时,抛物线在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.函数y=a(x-h)2(a≠0)的图象和性质3.当a>0时,在对称轴(x=h)的左侧,y随着x的增大而减小;在对称轴(x=h)右侧,y随着x的增大而增大;当x=h时函数y的值最小(是0).
当a<0时,在对称轴(x=h)的左侧,y随着x的增大而增大;在对称轴(x=h)的右侧,y随着x增大而减小;当x=h时,函数y的值最大(是0).直线x=h二次函数y=a(x-h)2的性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=a(x-h)2 (a>0)y=a(x-h)2 (a<0)(h,0)(h,0)直线x=h直线x=h在x轴的上方(除顶点外)在x轴的下方( 除顶点外)向上向下当x=h时,最小值为0.当x=h时,最大值为0.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 3、把抛物线向左平移 3 个单位,可得到抛物线 .右427.2 二次函数的图象与性质(第2课时)华东师大版九年级(下册)你能用配方的方法把y=3x2-6x+5变形成
y=a(x-h)2+k的形式吗?函数y=ax2+bx+c的图象 二次函数y=3x2-6x+5的图象是什么形状?它与我们已经作过的二次函数的图象有什么关系? 在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象. 由于y=3x2-6x+5=3(x-1)2+2,因此我们先作二次函数y=3(x-1)2的图象. 观察图象,回答问题(1)函数y=3(x-1)2的图象与y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么? (2)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x-1)2的值随x的增大而减少? 我思考,我进步在同一坐标系中作出二次函数y=3x2,y=3(x-1)2和y=3(x-1)2+2的图象. 二次函数y=3x2,y=3(x-1)2和y=3(x-1)2+2的图象有什么关系?
它们的开口方向,对称轴和顶点坐标分别是什么?作图看一看. 对称轴仍是平行于y轴的直
线(x=1);增减性与y=3x2类似. 顶点是(1,2).二次函数y=3(x-1)2+2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
上平移2个单位后得到的.二次函数y=3(x-1)2+2的图象和抛物线y=3x2,y=3(x-1)2有什么关系?它的开口方向,对称轴和顶点坐标分别是什么?开口向上,当
X=1时有最小
值:且最小值=2.先猜一猜,再做一做,在同一坐标系中作二次函数y=3(x-1)2-2,会是什么样?X=1对称轴仍是平行于y轴的直线
(x=1);增减性与y=3x2类似. 顶点是(1,-2).二次函数y=3(x-1)2-2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
下平移2个单位后得到的.二次函数y=3(x-1)2-2的图象与抛物线y=3x2和y=3(x-1)2有何关系?它的开口方向、对称轴和顶点坐标分别是什么? 开口向上,
当x=1时y有
最小值:且
最小值= -2.想一想,二次函数y=-3(x-1)2+2和y=-3x2,y=-3(x-1)2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?再作图看一看.X=1我思考,我进步 在同一坐标系中作出二次函数
y=-3(x-1)2+2,y=-3(x-1)2-2,y=-3x2和
y=-3(x-1)2的图象 二次函数y=-3(x-1)2+2与y=-3(x-1)2-2和y=-3x2,y=-3(x-1)2的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小? 对称轴仍是平行于y轴的直线
(x=1);增减性与y= -3x2类似. 顶点分别是
(1,2)和(1,-2).二次函数y=-3(x-1)2+2与
y=-3(x-1)2+2的图象可
以看作是抛物线y=-3x2
先沿着x轴向右平移1个
单位,再沿直线x=1向上
(或向下)平移2个单位后
得到的.二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物
线y=-3x2,y=-3(x-1)2有什
么关系? 它的开口方向,对
称轴和顶点坐标分别是什
么?开口向下,
当x=1时y有
最大值:且
最大值= 2
(或最大值=-2).想一想,二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x2,y=-3(x+1)2yX=1对称轴仍是平行于y轴的直线
(x=-1);增减性与y= -3x2类似. 顶点分别是
(-1,2)和(-1,-2)..二次函数y=-3(x+1)2+2与
y=-3(x+1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向左平移1个
单位,再沿直线x=-1向上
(或向下)平移2个单位后
得到的.二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x2,y=-3(x+1)2有什么关系? 它的开口方向,对称轴和顶点坐标分别是什么?开口向下,
当x=-1时y有
最大值:且
最大值= 2
(或最大值= - 2).先想一想,再总结二次函数y=a(x-h)2+k的图象和性质. x=1二次函数y=a(x-h)2+k与y=ax2的关系一般地,由y=ax2的图象便可得到二次函数y=a(x-h)2+k的图象:y=a(x-h)2+k(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
因此,二次函数y=a(x-h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关. 二次函数y=a(x+h)2+k的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=a(x-h)2+k(a>0)y=a(x-h)2+k(a<0)(h,k)(h,k)直线x=h直线x=h由h和k的符号确定由h和k的符号确定向上向下当x=h时,最小值为k.当x=h时,最大值为k.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:1.指出下列函数图象的开口方向对称轴和顶点坐标:2.(1)二次函数y=3(x+1)2的图象与二次函数y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
(2)二次函数y=-3(x-2)2+4的图象与二次函数y=-3x2的图象有什么关系?
对于二次函数y=3(x+1)2,当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?二次函数y=3(x+1)2+4呢? 2.不同点: 只是位置不同(1)顶点不同:分别是(h,k)和(0,0).
(2)对称轴不同:分别是直线x= h和y轴.
(3)最值不同:分别是k和0.
3.联系: y=a(x-h)2+k(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 . 二次函数y=a(x-h)2+k与y=ax2的关系1.指出下列函数图象的开口方向,对称轴和顶点坐标.必要时作出草图进行验证.2.填写下表:27.2二次函数的图象和性质(第5课时)华东师大版九年级(下册)回答问题: 说出下列函数的开口方向、对称轴、顶点坐标: 函数y=ax2+bx+c的对称轴,顶点坐标是什么? 回答问题: 1. 说出下列函数的开口方向、对称轴、顶点坐标:例:指出抛物线:的开口方向,求出它的对称轴、顶点坐标、与y轴的交点坐标、与x轴的交点坐标。并画出草图。 对于y=ax2+bx+c我们可以确定它的开口
方向,求出它的对称轴、顶点坐标、与y轴
的交点坐标、与x轴的交点坐标(有交点时)
,这样就可以画出它的大致图象。练习 指出下列抛物线的开口方向、求出
它的对称轴、顶点坐标、与y轴的交
点坐标、与x轴的交点坐标。并画出
草图。 B1.抛物线y=2x2+8x-11的顶点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.不论k 取任何实数,抛物线y=a(x+k)2+k(a≠0)的
顶点都在
A.直线y = x上 B.直线y = - x上
C.x轴上 D.y轴上
3.若二次函数y=ax2 + 4x+a-1的最小值是2,则a的值是
4 B. -1 C. 3 D.4或-1
4.若二次函数 y=ax2 + b x + c 的图象如下,与x
轴的一个交点为(1,0),则下列
各式中不成立的是( )
A.b2-4ac>0 B.abc>0
C.a+b+c=0 D.a-b+c<01CAxyo-1 B( )
( ) 5.若把抛物线y=x2+bx+c向左平移2个单位,再向上平
移3个单位,得抛物线y = x2 - 2x+1,则
A.b=2 B.b=-6,c=6
C.b=-8 D.b=-8,c=18
6.若一次函数 y= ax + b 的图象经过第二、三、四象限,
则二次函数y = ax2 + bx - 3的大致图象是 ( )( )
B
-3-3-3-3C
7.在同一直角坐标系中,二次函数y=ax2+bx+c与一次函数y=ax+c的大致图象可能是 ( )C
27.2二次函数的图象和性质(第6课时)华东师大版九年级(下册)问题1如图,要用长为20m的铁栏杆,一面靠
墙,围成一个矩形的花圃,怎样围法才
能使围成的花圃面积最大?根据题意,得
y=-2x2+20x(0<x<10)配方,得
y=-2(x-5)2+50。函数图象开口向下,顶点坐标为(5,50),即当x=5时,函数取得最大值50.所以当AB长为5m,BC长为10m时,花圃的面积最大,为50m2.问题2某商店将每件进价为8元的某种商品按每
件10元出售,一天可销出约100件。该店
想通过降低售价、增加销售量的办法来提
高利润。经过市场调查,发现这种商品单
价每降低0.1元,其销售量可增加约10件。
将这种商品的售价降低多少时,能使销售
利润最大?
根据题意,得关系式为
y=-100x2+100x+200(02≤x≤2)你能完成吗?例 5用6 m长的铝合金型材做一个形状如图所示的
矩形窗框.应做成长、宽各为多少时,才能
使做成的窗框的透光面积最大?最大透光面
积是多少?即
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值。解这类题目的一般步骤在实际问题中,自变量往往是有一定取值范围的.因此,在根据二次函数的顶点坐标,求出当自变量取某个值时,二次函数取最大值(或最小值),还要根据实际问题检验自变量的这一取值是否在取值范围内,才能得到最后的结论.注意(1)设矩形的一边AB=xm,那么AD边的长度如何表示?
(2)设矩形的面积为ym2,当x取何值时,y的值最大?最大值是多少?如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.xmbm练一练1何时窗户通过的光线最多某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?练一练2 用48米长的竹篱笆围建一矩形养鸡场,养
鸡场一面用砖砌成,另三面用竹篱笆围成,并且在与砖墙相对的一面开2米宽的门(不用篱笆),问养鸡场的边长为多少米时,养鸡场占地面积最大?最大面积是多少?ym2xmxm练一练3 正方形ABCD边长5cm,等腰三角形PQR中,PQ=PR=5cm,
QR=8cm,点D、C、Q、R在同一直线l上,当C、Q两
点重合时,等腰△PQR以1cm/s的速度沿直线l向
左方向开始匀速运动,ts后正方形与等腰三角形
重合部分面积为Scm2,解答下列问题:
(1)当t=3s时,求S的值;
(2)当t=3s时,求S的值;
(3)当5s≤t≤8s时,求S
与t的函数关系式,并求
S的最大值。练一练4课堂小结这节课,你学到了什么?27.2二次函数的图象与性质(第7课时)华东师大版九年级(下册)(1)一般式(2)顶点式回味知识点:顶点坐标(h,k)目前接触的二次函数的关系式有哪些?例6 一个二次函数的图象过点(0,1),它的顶点坐标是(8,9),求这个二次函数的关系式。已知:二次函数的图像的顶点的坐标是(1,4),并且抛物线与x轴的两个交点的距离是4,求这个函数的解析式。 练一练练一练
已知:二次函数的图像的对称轴为直线
x= –3,并且函数有最大值为5,图像经过点
(–1,–3),求这个函数的解析式。 解:由题意可知,该函数的顶点的坐标是(-3,5), 所以,设y=a(x+3)2+5又抛物线经过点(-1,-3),得 -3=a(-1+3)2+5 ∴ a=-2∴所求的函数解析式为y= –2(x+3)2+5即y= –2x2–12x–13例7 一个二次函数的图象过(0,1)、(2,4)、(3,10)三点,求这个二次函数关系式.解: 设所求二次函数为y=ax2+bx+c,有这个函数的图象过(0,1),可得c=1.
又由图象过(2,4)、(3,10),得
解得
因此,所求二次函数的关系式是已知:二次函数的图像经过点A(–1,6)、B(3,0)、C(0,3),求这个函数的解析式。解:设所求函数解析式为y=ax2+bx+c .由已知函数图象过(-1,6),(3,0),(0,3)三点得 解这个方程组得a= 0.5,b= – 2.5,c=3 ∴所求得的函数解析式为y=0.5x2 – 2.5x+3练一练已知:抛物线y=ax2+bx+c过直线 与x轴、y轴的交点,且过(1,1),求抛物线的解析式.分析:∵直线 与x轴、y轴的交点为(2,0),(0,3)则:练一练* 交点式拓广探索*例 已知:如图,求二次函数关系式y=ax2+bx+c.解:如图,由题意得:抛物线与x轴交点的横坐标为-1和3∴设所求函数关系式为y=a(x+1)(x-3)∵图象过点(0,3)∴3=a(0+1)(0-3) ∴a=-1∴所求的函数关系式为y=-(x+1)(x-3) 即y= –x2+2x+3拓广探索例 已知:抛物线与坐标轴交于A,B,C三个点,其中A的坐标为(-1,0),B的坐标为(3,0),并且△ABC的面积是6,求这个函数的解析式。 分析:由题意可知OC的长是3,所以点C的坐标为(0,3)或(0,-3)当C(0,3)时,
函数的解析式为:
y=-x2+2x+3 当C(0,-3)时,函数的解析式为: -y=-x2+2x+3,即y=x2-2x-3 拓广探索二次函数解析式的确定:归纳小结求二次函数解析式可用待定系数法.
(1)当已知图象上任意三点的坐标或已知三对对应值时,使用一般式:
来解;
(2)当已知顶点坐标或最值时,使 用顶点式 来解,比较简单。二次函数解析式的确定:归纳小结(3)过与x轴的两个交点和一普通点的二次函数解析式确定.
交点式
九年级(下)数学教学课件27.2 二次函数的图象与性质华东师大版九年级(下册)(第1课时)函数y=ax2+bx+c (a,b,c是常数,a≠ 0) 叫做x的二次函数.什么叫二次函数?我们学过用什么方法画函数
的图象?主要有哪些步骤?观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表:用描点法画二次函数y=x2的图象0123…0149…描点,连线y=x2观察图象,回答问题串(1)你能描述图象的形状吗?与同伴进行交流.(2)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流.观察图象,回答问题串(3)图象 与x轴有交点吗?如果有,交点坐标是什么?(4)在对称轴左侧,随着x值的增大,y 的值如何变化?在对称轴右侧呢?观察图象,回答问题串(5)当x取什么值时,y的值最小?最小值是什么?你是如何知道的?这条抛物线关于
y轴对称,y轴就
是它的对称轴. 对称轴与抛物
线的交点叫做
抛物线的顶点.二次函数y=x2的
图象形如物体抛射
时所经过的路线,我
们把它叫做抛物线.在对称轴的左
侧时,y随着x的
增大而减小. 在对称轴的右
侧时, y随着x的
增大而增大. 抛物线y=x2在x轴的上方(除顶点外),
顶点是它的最低点,开口向上,并且向
上无限伸展;当x=0时,函数y的值最小,
最小值是0.(1)二次函数y=-x2的图象是什么形状?(2)它与二次函数y=x2的图象有什么关系?你能根据表格中的数据作出猜想吗?xy0-4-3-2-11234-10-8-6-4-22-1描点,连线y=-x2这条抛物线关于
y轴对称,y轴就
是它的对称轴. 对称轴与抛物
线的交点叫做
抛物线的顶点.yy在对称轴的左侧
时,y随着x的增大
而增大. 在对称轴的右侧
时, y随着x的增大
而减小. y抛物线y= -x2在x轴的下方(除顶点外),
顶点是它的最高点,开口向下,并且向下
无限伸展;当x=0时,函数y的值最大,
最大值是0.抛物线顶点坐标对称轴位置开口方向增减性最值y=x2y= -x2(0,0)(0,0)y轴y轴在x轴的上方(除顶点外)在x轴的下方( 除顶点外)向上向下当x=0时,最小值为0.当x=0时,最大值为0.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 函数y=ax2(a≠0)的图象和性质:y=x2y=-x21.顶点坐标与对称轴2.位置与开口方向3.增减性与最值1.抛物线y=ax2的顶点是原点,对称轴是y轴.2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.二次函数y=ax2的性质1.已知抛物线y=ax2经过点A(-2,-8)
(1)求此抛物线的函数解析式;
(2)判断点B(-1,-4)是否在此抛物线上;
(3)求出此抛物线上纵坐标为-6的点的坐标;
(4)若点(m,n)在此抛物线上,那么点
(-m,n)是否在此抛物线上?点(m,-n)呢?2.填空:
(1)抛物线y=2x2的顶点坐标是_____;
对称轴是______;在___________ 侧,
y随着x的增大而增大;在_________侧,
y随着x的增大而减小;当x= 时,函数y的值最小,最小值是 ;抛物线y=2x2在x轴的 方(除顶点外).(0,0)y轴对称轴的左0对称轴的右0上(2)抛物线 在x轴的 方(除顶点外),
当x_____时,y随着x的增大而增大;
当x_____时,y随着x的,增大而减小
当x=0时,函数y的值最大,最大值是_____,
当x 0时,y<0.下0<0>0回味无穷2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;
在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;
在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.1.抛物线y=ax2的顶点是原点,对称轴是y轴.由二次函数y=x2和y=-x2知:27.2 二次函数的图象与性质(第2课时)华东师大版九年级(下册)比较二次函数 y=x2 和 y= –x2 图象的异同:二次函数 y=2x2 的图象是什么形状?它与二次函数 y=x2 的图象有什么相同和不同?(1)二次函数 y=2x2+1 的图象与二次函数 y=2x2 的图象有什么关系?(2)二次函数 y=3x2-1 的图象与二次函数 y=3x2 的图象有什么关系?y在同一直角坐标系中画出函数
的图像试说出函数y=ax2+k(a、k是常数,a≠0)的图象的开口方向、对称轴和顶点坐标,并填写下表. 向上向下y轴y轴(0,k)(0,k)练习
1.把抛物线 向下平移2个单位,可以得到抛物线 ,在向上平移5个单位,可以得到抛物线 ;
2.对于函数y= –x2+1,当x 时,函数值y随x的增大而增大;当x 时,函数值y随x的增大而减小;当x 时,函数取得最 值,为 。<0>0=0大03.函数y=3x2+5与y=3x2的图象的不同之处是( )
A.对称轴 B.开口方向
C.顶点 D.形状
4.已知抛物线y=2x2-1上有两点(x1,y1 ) ,(x1,y1 )且x1<x2<0,则y1 y2(填“<”或“>”)C<5.已知一个二次函数图像的顶点在y轴上,并且离原点1个单位,图像经过点(–1,0),求该二次函数解析式。
6.已知抛物线 ,把它向下平移,得到的抛物线与x轴交于A、B两点,与y轴交于C点,若⊿ABC是直角三角形,那么原抛物线应向下平移几个单位?27.2二次函数的图象与性质(第3课时)华东师大版九年级(下册)1.抛物线y=ax2的顶点是原点,对称轴是y轴.2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外), 它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.二次函数y=ax2的性质在同一个直角坐标系里画出函数 与 的图象.xy0-8-6-4-2246820161284-2描点,连线1012-10-122观察这两个函数的图象,
它们有什么关系?xy0-8-6-4-2246820161284-2描点,连线1012-10-1222xyO函数y= (x-2)2的图象与y= x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么? 二次项系数
相同 a>0,
开口都向上,两个二次函数的图象
形状相同,可以看作是
抛物线y= x2整体
沿x轴向右平移了2
个单位2xyO函数y= (x-2)2的图象与y= x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么? 顶点坐标
是点(2,0).图象是轴对称图形
对称轴是平行于
y轴的直线:x=2.2xyOx取哪些值时,函数y= (x-1)2的值随x值的增大而减小?x取哪些值时,函数y= (x-1)2的值随x的增大而增大? 在对称轴(直线:x=2)
左侧(即x<2时), y的值
随x的增大而减小,.在对称轴(直线:x=2)
右侧(即x>2时), y的值
随x的增大而增大,.顶点是最低点,函数
有最小值.当x=2时,
最小值是0..想一想, 这个函数的图象和性质会是什么样? 在同一个直角坐标系里画出 函数 和 的图象 xy0-8-6-4-2246820161284-2描点,连线1012-10-122观察函数 与 的
图象,它们有什么关系?xy0-8-6-4-2246820161284-2描点,连线1012-10-122函数 与 的
图象有什么关系?说出它
的顶点坐标和对称轴直线x=-2函数 的图象可以看成由
的图象向_____平移___个单位得到,它们的形状和开口大小相同函数 的图象可以看成由
的图象向____平移___个单位得到,它们的形状和开口大小相同这里的平移方向有什么规律?右左22函数y=a(x-h)2(a≠0)的图象和性质1.函数y=a(x-h)2(a≠0)的图象可
由函数y=ax2的图象平移得到.
当h>0 时,向___平移___个单位
当h<0 时,向___平移____个单位
对称轴为:_________.顶点为____h|h|右左直线x=h(h,0)2.当a>0时,抛物线在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.函数y=a(x-h)2(a≠0)的图象和性质3.当a>0时,在对称轴(x=h)的左侧,y随着x的增大而减小;在对称轴(x=h)右侧,y随着x的增大而增大;当x=h时函数y的值最小(是0).
当a<0时,在对称轴(x=h)的左侧,y随着x的增大而增大;在对称轴(x=h)的右侧,y随着x增大而减小;当x=h时,函数y的值最大(是0).直线x=h二次函数y=a(x-h)2的性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=a(x-h)2 (a>0)y=a(x-h)2 (a<0)(h,0)(h,0)直线x=h直线x=h在x轴的上方(除顶点外)在x轴的下方( 除顶点外)向上向下当x=h时,最小值为0.当x=h时,最大值为0.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 3、把抛物线向左平移 3 个单位,可得到抛物线 .右427.2 二次函数的图象与性质(第2课时)华东师大版九年级(下册)你能用配方的方法把y=3x2-6x+5变形成
y=a(x-h)2+k的形式吗?函数y=ax2+bx+c的图象 二次函数y=3x2-6x+5的图象是什么形状?它与我们已经作过的二次函数的图象有什么关系? 在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象. 由于y=3x2-6x+5=3(x-1)2+2,因此我们先作二次函数y=3(x-1)2的图象. 观察图象,回答问题(1)函数y=3(x-1)2的图象与y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么? (2)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x-1)2的值随x的增大而减少? 我思考,我进步在同一坐标系中作出二次函数y=3x2,y=3(x-1)2和y=3(x-1)2+2的图象. 二次函数y=3x2,y=3(x-1)2和y=3(x-1)2+2的图象有什么关系?
它们的开口方向,对称轴和顶点坐标分别是什么?作图看一看. 对称轴仍是平行于y轴的直
线(x=1);增减性与y=3x2类似. 顶点是(1,2).二次函数y=3(x-1)2+2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
上平移2个单位后得到的.二次函数y=3(x-1)2+2的图象和抛物线y=3x2,y=3(x-1)2有什么关系?它的开口方向,对称轴和顶点坐标分别是什么?开口向上,当
X=1时有最小
值:且最小值=2.先猜一猜,再做一做,在同一坐标系中作二次函数y=3(x-1)2-2,会是什么样?X=1对称轴仍是平行于y轴的直线
(x=1);增减性与y=3x2类似. 顶点是(1,-2).二次函数y=3(x-1)2-2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
下平移2个单位后得到的.二次函数y=3(x-1)2-2的图象与抛物线y=3x2和y=3(x-1)2有何关系?它的开口方向、对称轴和顶点坐标分别是什么? 开口向上,
当x=1时y有
最小值:且
最小值= -2.想一想,二次函数y=-3(x-1)2+2和y=-3x2,y=-3(x-1)2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?再作图看一看.X=1我思考,我进步 在同一坐标系中作出二次函数
y=-3(x-1)2+2,y=-3(x-1)2-2,y=-3x2和
y=-3(x-1)2的图象 二次函数y=-3(x-1)2+2与y=-3(x-1)2-2和y=-3x2,y=-3(x-1)2的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小? 对称轴仍是平行于y轴的直线
(x=1);增减性与y= -3x2类似. 顶点分别是
(1,2)和(1,-2).二次函数y=-3(x-1)2+2与
y=-3(x-1)2+2的图象可
以看作是抛物线y=-3x2
先沿着x轴向右平移1个
单位,再沿直线x=1向上
(或向下)平移2个单位后
得到的.二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物
线y=-3x2,y=-3(x-1)2有什
么关系? 它的开口方向,对
称轴和顶点坐标分别是什
么?开口向下,
当x=1时y有
最大值:且
最大值= 2
(或最大值=-2).想一想,二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x2,y=-3(x+1)2yX=1对称轴仍是平行于y轴的直线
(x=-1);增减性与y= -3x2类似. 顶点分别是
(-1,2)和(-1,-2)..二次函数y=-3(x+1)2+2与
y=-3(x+1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向左平移1个
单位,再沿直线x=-1向上
(或向下)平移2个单位后
得到的.二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x2,y=-3(x+1)2有什么关系? 它的开口方向,对称轴和顶点坐标分别是什么?开口向下,
当x=-1时y有
最大值:且
最大值= 2
(或最大值= - 2).先想一想,再总结二次函数y=a(x-h)2+k的图象和性质. x=1二次函数y=a(x-h)2+k与y=ax2的关系一般地,由y=ax2的图象便可得到二次函数y=a(x-h)2+k的图象:y=a(x-h)2+k(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
因此,二次函数y=a(x-h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关. 二次函数y=a(x+h)2+k的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=a(x-h)2+k(a>0)y=a(x-h)2+k(a<0)(h,k)(h,k)直线x=h直线x=h由h和k的符号确定由h和k的符号确定向上向下当x=h时,最小值为k.当x=h时,最大值为k.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:1.指出下列函数图象的开口方向对称轴和顶点坐标:2.(1)二次函数y=3(x+1)2的图象与二次函数y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
(2)二次函数y=-3(x-2)2+4的图象与二次函数y=-3x2的图象有什么关系?
对于二次函数y=3(x+1)2,当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?二次函数y=3(x+1)2+4呢? 2.不同点: 只是位置不同(1)顶点不同:分别是(h,k)和(0,0).
(2)对称轴不同:分别是直线x= h和y轴.
(3)最值不同:分别是k和0.
3.联系: y=a(x-h)2+k(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 . 二次函数y=a(x-h)2+k与y=ax2的关系1.指出下列函数图象的开口方向,对称轴和顶点坐标.必要时作出草图进行验证.2.填写下表:27.2二次函数的图象和性质(第5课时)华东师大版九年级(下册)回答问题: 说出下列函数的开口方向、对称轴、顶点坐标: 函数y=ax2+bx+c的对称轴,顶点坐标是什么? 回答问题: 1. 说出下列函数的开口方向、对称轴、顶点坐标:例:指出抛物线:的开口方向,求出它的对称轴、顶点坐标、与y轴的交点坐标、与x轴的交点坐标。并画出草图。 对于y=ax2+bx+c我们可以确定它的开口
方向,求出它的对称轴、顶点坐标、与y轴
的交点坐标、与x轴的交点坐标(有交点时)
,这样就可以画出它的大致图象。练习 指出下列抛物线的开口方向、求出
它的对称轴、顶点坐标、与y轴的交
点坐标、与x轴的交点坐标。并画出
草图。 B1.抛物线y=2x2+8x-11的顶点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.不论k 取任何实数,抛物线y=a(x+k)2+k(a≠0)的
顶点都在
A.直线y = x上 B.直线y = - x上
C.x轴上 D.y轴上
3.若二次函数y=ax2 + 4x+a-1的最小值是2,则a的值是
4 B. -1 C. 3 D.4或-1
4.若二次函数 y=ax2 + b x + c 的图象如下,与x
轴的一个交点为(1,0),则下列
各式中不成立的是( )
A.b2-4ac>0 B.abc>0
C.a+b+c=0 D.a-b+c<01CAxyo-1 B( )
( ) 5.若把抛物线y=x2+bx+c向左平移2个单位,再向上平
移3个单位,得抛物线y = x2 - 2x+1,则
A.b=2 B.b=-6,c=6
C.b=-8 D.b=-8,c=18
6.若一次函数 y= ax + b 的图象经过第二、三、四象限,
则二次函数y = ax2 + bx - 3的大致图象是 ( )( )
B
-3-3-3-3C
7.在同一直角坐标系中,二次函数y=ax2+bx+c与一次函数y=ax+c的大致图象可能是 ( )C
27.2二次函数的图象和性质(第6课时)华东师大版九年级(下册)问题1如图,要用长为20m的铁栏杆,一面靠
墙,围成一个矩形的花圃,怎样围法才
能使围成的花圃面积最大?根据题意,得
y=-2x2+20x(0<x<10)配方,得
y=-2(x-5)2+50。函数图象开口向下,顶点坐标为(5,50),即当x=5时,函数取得最大值50.所以当AB长为5m,BC长为10m时,花圃的面积最大,为50m2.问题2某商店将每件进价为8元的某种商品按每
件10元出售,一天可销出约100件。该店
想通过降低售价、增加销售量的办法来提
高利润。经过市场调查,发现这种商品单
价每降低0.1元,其销售量可增加约10件。
将这种商品的售价降低多少时,能使销售
利润最大?
根据题意,得关系式为
y=-100x2+100x+200(02≤x≤2)你能完成吗?例 5用6 m长的铝合金型材做一个形状如图所示的
矩形窗框.应做成长、宽各为多少时,才能
使做成的窗框的透光面积最大?最大透光面
积是多少?即
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值。解这类题目的一般步骤在实际问题中,自变量往往是有一定取值范围的.因此,在根据二次函数的顶点坐标,求出当自变量取某个值时,二次函数取最大值(或最小值),还要根据实际问题检验自变量的这一取值是否在取值范围内,才能得到最后的结论.注意(1)设矩形的一边AB=xm,那么AD边的长度如何表示?
(2)设矩形的面积为ym2,当x取何值时,y的值最大?最大值是多少?如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.xmbm练一练1何时窗户通过的光线最多某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?练一练2 用48米长的竹篱笆围建一矩形养鸡场,养
鸡场一面用砖砌成,另三面用竹篱笆围成,并且在与砖墙相对的一面开2米宽的门(不用篱笆),问养鸡场的边长为多少米时,养鸡场占地面积最大?最大面积是多少?ym2xmxm练一练3 正方形ABCD边长5cm,等腰三角形PQR中,PQ=PR=5cm,
QR=8cm,点D、C、Q、R在同一直线l上,当C、Q两
点重合时,等腰△PQR以1cm/s的速度沿直线l向
左方向开始匀速运动,ts后正方形与等腰三角形
重合部分面积为Scm2,解答下列问题:
(1)当t=3s时,求S的值;
(2)当t=3s时,求S的值;
(3)当5s≤t≤8s时,求S
与t的函数关系式,并求
S的最大值。练一练4课堂小结这节课,你学到了什么?27.2二次函数的图象与性质(第7课时)华东师大版九年级(下册)(1)一般式(2)顶点式回味知识点:顶点坐标(h,k)目前接触的二次函数的关系式有哪些?例6 一个二次函数的图象过点(0,1),它的顶点坐标是(8,9),求这个二次函数的关系式。已知:二次函数的图像的顶点的坐标是(1,4),并且抛物线与x轴的两个交点的距离是4,求这个函数的解析式。 练一练练一练
已知:二次函数的图像的对称轴为直线
x= –3,并且函数有最大值为5,图像经过点
(–1,–3),求这个函数的解析式。 解:由题意可知,该函数的顶点的坐标是(-3,5), 所以,设y=a(x+3)2+5又抛物线经过点(-1,-3),得 -3=a(-1+3)2+5 ∴ a=-2∴所求的函数解析式为y= –2(x+3)2+5即y= –2x2–12x–13例7 一个二次函数的图象过(0,1)、(2,4)、(3,10)三点,求这个二次函数关系式.解: 设所求二次函数为y=ax2+bx+c,有这个函数的图象过(0,1),可得c=1.
又由图象过(2,4)、(3,10),得
解得
因此,所求二次函数的关系式是已知:二次函数的图像经过点A(–1,6)、B(3,0)、C(0,3),求这个函数的解析式。解:设所求函数解析式为y=ax2+bx+c .由已知函数图象过(-1,6),(3,0),(0,3)三点得 解这个方程组得a= 0.5,b= – 2.5,c=3 ∴所求得的函数解析式为y=0.5x2 – 2.5x+3练一练已知:抛物线y=ax2+bx+c过直线 与x轴、y轴的交点,且过(1,1),求抛物线的解析式.分析:∵直线 与x轴、y轴的交点为(2,0),(0,3)则:练一练* 交点式拓广探索*例 已知:如图,求二次函数关系式y=ax2+bx+c.解:如图,由题意得:抛物线与x轴交点的横坐标为-1和3∴设所求函数关系式为y=a(x+1)(x-3)∵图象过点(0,3)∴3=a(0+1)(0-3) ∴a=-1∴所求的函数关系式为y=-(x+1)(x-3) 即y= –x2+2x+3拓广探索例 已知:抛物线与坐标轴交于A,B,C三个点,其中A的坐标为(-1,0),B的坐标为(3,0),并且△ABC的面积是6,求这个函数的解析式。 分析:由题意可知OC的长是3,所以点C的坐标为(0,3)或(0,-3)当C(0,3)时,
函数的解析式为:
y=-x2+2x+3 当C(0,-3)时,函数的解析式为: -y=-x2+2x+3,即y=x2-2x-3 拓广探索二次函数解析式的确定:归纳小结求二次函数解析式可用待定系数法.
(1)当已知图象上任意三点的坐标或已知三对对应值时,使用一般式:
来解;
(2)当已知顶点坐标或最值时,使 用顶点式 来解,比较简单。二次函数解析式的确定:归纳小结(3)过与x轴的两个交点和一普通点的二次函数解析式确定.
交点式
