2022--2023学年人教版八年级数学上册12.2.6一次函数与一次方程、一次不等式 课件(共20张PPT)
文档属性
| 名称 | 2022--2023学年人教版八年级数学上册12.2.6一次函数与一次方程、一次不等式 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 311.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 19:07:57 | ||
图片预览







文档简介
(共20张PPT)
12.2.6 一次函数与一元一次方程、一元一次不等式(组)
本课目标:
1.理解一次函数与一元一次方程、一元一次不等式的关系
2.理解函数图像与方程的解、不等式解集的关系
3.借助图像帮助解方程、求解集
思考:前面,已经学过一元一次方程和一元一次不等式的解法,
它们与一次函数之间有什么联系呢?
求一次函数 y=2x+6 中y=0时
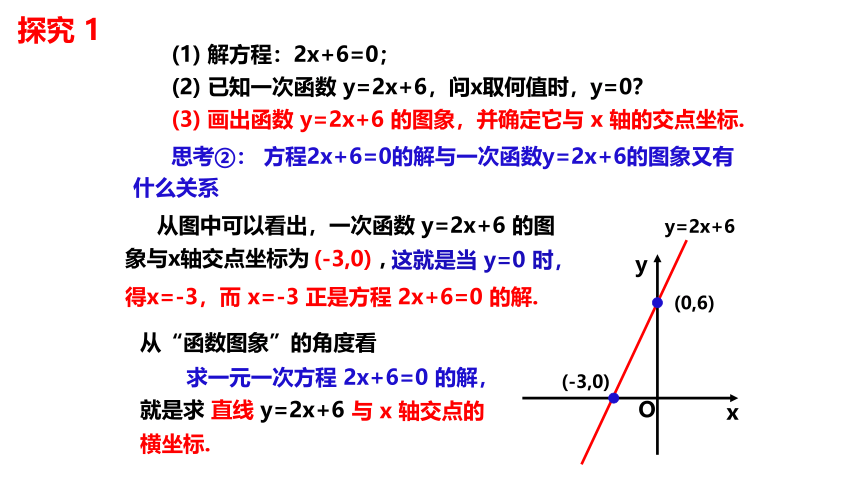
(1) 解方程:2x+6=0;
(2) 已知一次函数 y=2x+6,问x取何值时,y=0?
探究 1
思考①:这两个问题有什么关系?
从“函数值”的角度看
求一元一次方程 2x+6=0 的解,
可转化为
x的值.
(1) 解方程:2x+6=0;
(2) 已知一次函数 y=2x+6,问x取何值时,y=0?
探究 1
思考②: 方程2x+6=0的解与一次函数y=2x+6的图象又有什么关系
(3) 画出函数 y=2x+6 的图象,并确定它与 x 轴的交点坐标.
O
x
y
(0,6)
(-3,0)
y=2x+6
从图中可以看出,一次函数 y=2x+6 的图象与x轴交点坐标为 ,
(-3,0)
这就是当 y=0 时,
得x=-3,
而 x=-3 正是方程 2x+6=0 的解.
从“函数图象”的角度看
求一元一次方程 2x+6=0 的解,
就是求
直线 y=2x+6
与 x 轴交点的横坐标.
归纳与总结
一次函数与一元一次方程的关系
因为,任何一个一元一次方程
都可转化为 kx+b=0 的形式,
所以解一元一次方程 kx+b=0,
都可转化为求一次函数 y=kx+b (k,b为常数,且k≠0) 中 y=0 时的 x值 .
从图象上看,
就是求直线 y=kx+b
与 x轴交点的横坐标.
函数y=kx+b中,函数值y=0时自变量x的值是方程kx+b=0的解
函数y=kx+b的图像与x轴交点的横坐标是方程kx+b=0的解
数
形
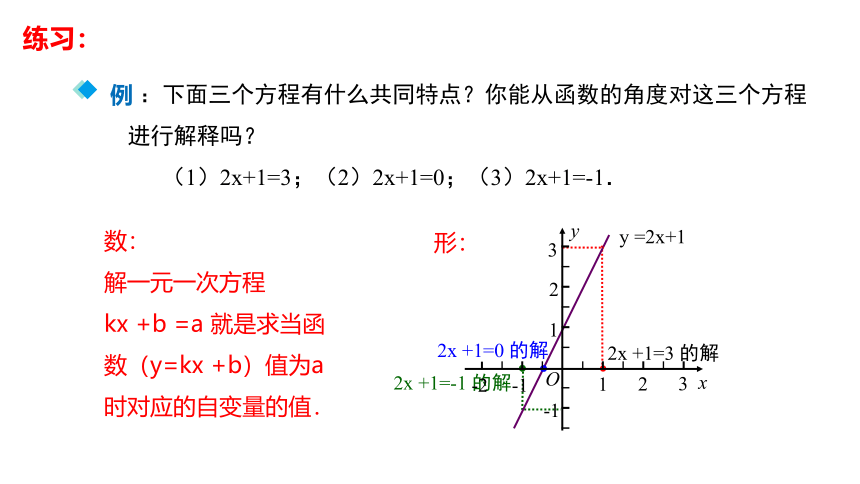
:下面三个方程有什么共同特点?你能从函数的角度对这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
数:
解一元一次方程
kx +b =a 就是求当函
数(y=kx +b)值为a
时对应的自变量的值.
2x +1=3 的解
y =2x+1
2x +1=0 的解
2x +1=-1 的解
例
练习:
3
2
1
2
1
-2
O
x
y
-1
-1
3
形:
例:已知一次函数 y=kx+b 的图像如图所示,请求出:
关于x的一次方程 kx+b=0 的解;
x
y
O
-2
1
x=-2
应用:未知方程式也能求方程
1.已知:一次函数y=0.8x-2与x轴的交点为(2.5,0),你能说出0.8x-2=0的解吗?
2.已知:一次函数y=kx-5与x轴的交点为(3,0),那么你能说出kx-5=0的解吗?
3.已知关于x的一元一次方程mx+n=0的解是-3,则直线y=mx+n与x轴的交点坐标是__________.
x=2.5
x=3
(-3,0)
随堂一练:
根据一次函数y=2x+6的图像,你能说出一元一次不等式2x+6>0的解集吗?
探究 2
O
x
y
(0,6)
(-3,0)
y=2x+6
x>-3
2x+6>0,
就是函数y=2x+6中函数值 y>0;
从图象上看,
y>0 就是指 x 轴上方的图象;
x 在什么范围时,图象在x轴的上方呢?
因为图象与x轴交于点(-3,0),
所以由图象可知,
应有x>-3.
要使y>0,
即2x+6>0,
根据一次函数y=2x+6的图像,你能说出一元一次不等式2x+6<0的解集了?
探究 3
O
x
y
(0,6)
(-3,0)
y=2x+6
x<-3
2x+6<0,
就是函数y=2x+6中函数值 y<0;
从图象上看,
y<0 就是指 x 轴下方的图象;
x 在什么范围时,图象在x轴的下方呢?
因为图象与x轴交于点(-3,0),
所以由图象可知,
应有x<-3.
要使y<0,
即2x+6<0,
因为,任何一个一元一次不等式都可以转化为 kx+b>0
的形式,
(或 kx+b<0)
解一元一次不等式 kx+b>0 (或 kx+b<0),
所以,
归纳与总结
一次函数与一元一次不等式的关系
就是求使一次函数 y=kx+b (k,b为常数,且k≠0)
取正值 (或负值) 时x的取值范围.
求kx+b>0
(或<0)的解
从”函数值”的角度看
就是求一次函数y=kx+b中y>0(或y<0)时,x的范围
求kx+b>0
(或<0)的解
从”函数图象”的角度看
就是求直线y= ax+b在x轴上方(或下方)部分所有点的横坐标
例:画出函数y=-3x+6的图象,结合图象:
⑴求方程-3x+6=0的解;
x
y
o
(2,0)
(0,6)
y=-3x+6
练习:
⑵ 求不等式-3x+6>0的解集;
⑶求不等式-3x+6≤0的解集;
⑷ 求不等式-3x+6≤6的解集.
(6)当-3(5)当y=-3时,求x的值;
1.已知一次函数y=kx+b的图像如图所示,请求出:
关于x的一次不等式kx+b<0的解集。
x<-2
x
y
O
-2
1
随堂小测:
1.如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是A.x=2 B.x=0 C.x=-1 D.x=-3
x
y
O
B
A
2.如图,直线y=kx+b过点A(2,1)和点B(-1,-2),则不等式-2x
y
O
B
A
3.如图,一次函数y=kx+b过点 (-1,0),则不等式k(x-1)+b>0的解集是________
x
y
O
-1
1
1
4.已知方程 的解是x=-2,下列为函数 的图像的是( )
x
y
O
方程化为 3x-6 =0
画出函数y=3x-6的图象
所以方程3x-6=0的解为x =2
y=3x-6
解法一:
由图象可以看出:
Y=0时x的值x=2
综合应用
用画函数图象的方法解方程:5x+4=2x+10
(2,0)
(0,-6)
即 方程5x+4=2x+10的解为 x=2
解法二:
把 5x+4=2x+10 看做两个一次函数y=5x+4和y=2x+10,
画出y=5x+4和y=2x+10的图象.
(0,10)
(0,-5)
y=2x+10
y=5x+4
它们的交点的横坐标为2.
当x =2时直线y=5x+4 上的纵坐标与直线y=2x+10的纵坐标相等.
x =2
x
y
O
(0,4)
由图象可知
即5x+4=2x+10
所以此方程的解为
2
x
y
O
不等式化为 3x-6 <0
画出函数y=3x-6的图象
所以不等式3x-6<0的解集为x <2
y=3x-6
解法一:
由图象可以看出:
y<0时x的取值范围是 x<2
综合应用
用画函数图象的方法解不等式:5x+4<2x+10
(2,0)
(0,-6)
即 不等式5x+4<2x+10的解集为 x<2
解法二:
把 5x+4<2x+10 看做两个一次函数y=5x+4和y=2x+10,
画出y=5x+4和y=2x+10的图象.
(0,10)
(0,-5)
y=2x+10
y=5x+4
它们的交点的横坐标为2.
当x <2时直线y=5x+4 上的点都在直线y=2x+10的下方.
x <2
x
y
O
(0,4)
由图象可知
即5x+4<2x+10
所以此不等式的解集为
2
练习:如图,直线y=2x-1与直线y=kx+b相交于点P(2,3),根据图像,不等式2x-1>kx+b的解集是________
12.2.6 一次函数与一元一次方程、一元一次不等式(组)
本课目标:
1.理解一次函数与一元一次方程、一元一次不等式的关系
2.理解函数图像与方程的解、不等式解集的关系
3.借助图像帮助解方程、求解集
思考:前面,已经学过一元一次方程和一元一次不等式的解法,
它们与一次函数之间有什么联系呢?
求一次函数 y=2x+6 中y=0时
(1) 解方程:2x+6=0;
(2) 已知一次函数 y=2x+6,问x取何值时,y=0?
探究 1
思考①:这两个问题有什么关系?
从“函数值”的角度看
求一元一次方程 2x+6=0 的解,
可转化为
x的值.
(1) 解方程:2x+6=0;
(2) 已知一次函数 y=2x+6,问x取何值时,y=0?
探究 1
思考②: 方程2x+6=0的解与一次函数y=2x+6的图象又有什么关系
(3) 画出函数 y=2x+6 的图象,并确定它与 x 轴的交点坐标.
O
x
y
(0,6)
(-3,0)
y=2x+6
从图中可以看出,一次函数 y=2x+6 的图象与x轴交点坐标为 ,
(-3,0)
这就是当 y=0 时,
得x=-3,
而 x=-3 正是方程 2x+6=0 的解.
从“函数图象”的角度看
求一元一次方程 2x+6=0 的解,
就是求
直线 y=2x+6
与 x 轴交点的横坐标.
归纳与总结
一次函数与一元一次方程的关系
因为,任何一个一元一次方程
都可转化为 kx+b=0 的形式,
所以解一元一次方程 kx+b=0,
都可转化为求一次函数 y=kx+b (k,b为常数,且k≠0) 中 y=0 时的 x值 .
从图象上看,
就是求直线 y=kx+b
与 x轴交点的横坐标.
函数y=kx+b中,函数值y=0时自变量x的值是方程kx+b=0的解
函数y=kx+b的图像与x轴交点的横坐标是方程kx+b=0的解
数
形
:下面三个方程有什么共同特点?你能从函数的角度对这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
数:
解一元一次方程
kx +b =a 就是求当函
数(y=kx +b)值为a
时对应的自变量的值.
2x +1=3 的解
y =2x+1
2x +1=0 的解
2x +1=-1 的解
例
练习:
3
2
1
2
1
-2
O
x
y
-1
-1
3
形:
例:已知一次函数 y=kx+b 的图像如图所示,请求出:
关于x的一次方程 kx+b=0 的解;
x
y
O
-2
1
x=-2
应用:未知方程式也能求方程
1.已知:一次函数y=0.8x-2与x轴的交点为(2.5,0),你能说出0.8x-2=0的解吗?
2.已知:一次函数y=kx-5与x轴的交点为(3,0),那么你能说出kx-5=0的解吗?
3.已知关于x的一元一次方程mx+n=0的解是-3,则直线y=mx+n与x轴的交点坐标是__________.
x=2.5
x=3
(-3,0)
随堂一练:
根据一次函数y=2x+6的图像,你能说出一元一次不等式2x+6>0的解集吗?
探究 2
O
x
y
(0,6)
(-3,0)
y=2x+6
x>-3
2x+6>0,
就是函数y=2x+6中函数值 y>0;
从图象上看,
y>0 就是指 x 轴上方的图象;
x 在什么范围时,图象在x轴的上方呢?
因为图象与x轴交于点(-3,0),
所以由图象可知,
应有x>-3.
要使y>0,
即2x+6>0,
根据一次函数y=2x+6的图像,你能说出一元一次不等式2x+6<0的解集了?
探究 3
O
x
y
(0,6)
(-3,0)
y=2x+6
x<-3
2x+6<0,
就是函数y=2x+6中函数值 y<0;
从图象上看,
y<0 就是指 x 轴下方的图象;
x 在什么范围时,图象在x轴的下方呢?
因为图象与x轴交于点(-3,0),
所以由图象可知,
应有x<-3.
要使y<0,
即2x+6<0,
因为,任何一个一元一次不等式都可以转化为 kx+b>0
的形式,
(或 kx+b<0)
解一元一次不等式 kx+b>0 (或 kx+b<0),
所以,
归纳与总结
一次函数与一元一次不等式的关系
就是求使一次函数 y=kx+b (k,b为常数,且k≠0)
取正值 (或负值) 时x的取值范围.
求kx+b>0
(或<0)的解
从”函数值”的角度看
就是求一次函数y=kx+b中y>0(或y<0)时,x的范围
求kx+b>0
(或<0)的解
从”函数图象”的角度看
就是求直线y= ax+b在x轴上方(或下方)部分所有点的横坐标
例:画出函数y=-3x+6的图象,结合图象:
⑴求方程-3x+6=0的解;
x
y
o
(2,0)
(0,6)
y=-3x+6
练习:
⑵ 求不等式-3x+6>0的解集;
⑶求不等式-3x+6≤0的解集;
⑷ 求不等式-3x+6≤6的解集.
(6)当-3
1.已知一次函数y=kx+b的图像如图所示,请求出:
关于x的一次不等式kx+b<0的解集。
x<-2
x
y
O
-2
1
随堂小测:
1.如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是A.x=2 B.x=0 C.x=-1 D.x=-3
x
y
O
B
A
2.如图,直线y=kx+b过点A(2,1)和点B(-1,-2),则不等式-2
y
O
B
A
3.如图,一次函数y=kx+b过点 (-1,0),则不等式k(x-1)+b>0的解集是________
x
y
O
-1
1
1
4.已知方程 的解是x=-2,下列为函数 的图像的是( )
x
y
O
方程化为 3x-6 =0
画出函数y=3x-6的图象
所以方程3x-6=0的解为x =2
y=3x-6
解法一:
由图象可以看出:
Y=0时x的值x=2
综合应用
用画函数图象的方法解方程:5x+4=2x+10
(2,0)
(0,-6)
即 方程5x+4=2x+10的解为 x=2
解法二:
把 5x+4=2x+10 看做两个一次函数y=5x+4和y=2x+10,
画出y=5x+4和y=2x+10的图象.
(0,10)
(0,-5)
y=2x+10
y=5x+4
它们的交点的横坐标为2.
当x =2时直线y=5x+4 上的纵坐标与直线y=2x+10的纵坐标相等.
x =2
x
y
O
(0,4)
由图象可知
即5x+4=2x+10
所以此方程的解为
2
x
y
O
不等式化为 3x-6 <0
画出函数y=3x-6的图象
所以不等式3x-6<0的解集为x <2
y=3x-6
解法一:
由图象可以看出:
y<0时x的取值范围是 x<2
综合应用
用画函数图象的方法解不等式:5x+4<2x+10
(2,0)
(0,-6)
即 不等式5x+4<2x+10的解集为 x<2
解法二:
把 5x+4<2x+10 看做两个一次函数y=5x+4和y=2x+10,
画出y=5x+4和y=2x+10的图象.
(0,10)
(0,-5)
y=2x+10
y=5x+4
它们的交点的横坐标为2.
当x <2时直线y=5x+4 上的点都在直线y=2x+10的下方.
x <2
x
y
O
(0,4)
由图象可知
即5x+4<2x+10
所以此不等式的解集为
2
练习:如图,直线y=2x-1与直线y=kx+b相交于点P(2,3),根据图像,不等式2x-1>kx+b的解集是________
