人教版六年级数学上册 比的意义 课件(共40张PPT)
文档属性
| 名称 | 人教版六年级数学上册 比的意义 课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 164.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 14:08:02 | ||
图片预览






文档简介
(共40张PPT)
六年级上册—人教版—数学—第四单元
比的意义
1.经历从具体情境中抽象出比的过程,体会认识比的必要
性,理解比的意义。
2.能正确读写比,会求比值,理解比与除法、分数的关系。3.能利用比的知识解释一些简单的生活问题,感受比在生
活中的广泛应用。
学习目标
情境导入
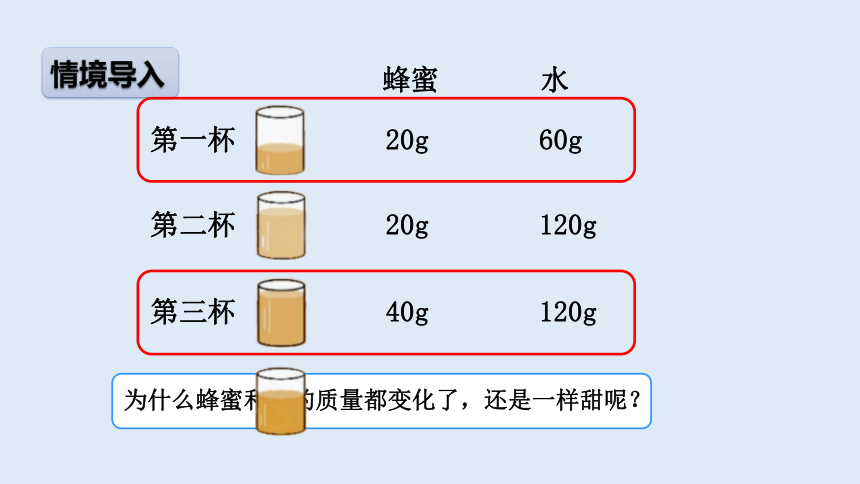
情境导入
第一杯
蜂蜜 水
20g
60g
120g
第三杯
40g
第二杯
20g
120g
第四杯
60g
60g
为什么蜂蜜和水的质量都变化了,还是一样甜呢?
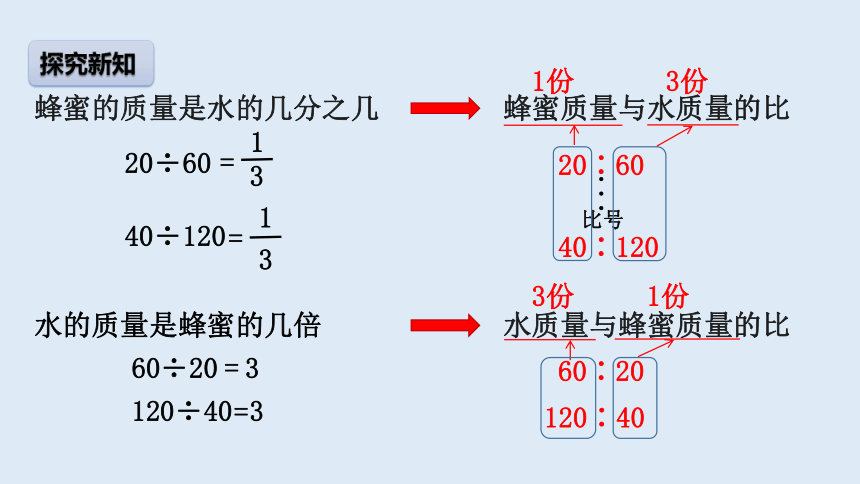
探究新知
水的质量是蜂蜜的几倍
蜂蜜的质量是水的几分之几
60÷20
20÷60
=
1
3
40÷120
=
1
3
120÷40
3
3
蜂蜜质量与水质量的比
20∶60
40∶120
60∶20
120∶40
比号
水质量与蜂蜜质量的比
1份
3份
1份
3份
...
=
=
第一杯
蜂蜜 水
20g
60g
探究新知
第二杯和第四杯蜂蜜水与第一杯一样甜吗?
太淡了
太甜了
为什么这两杯蜂蜜水与第一杯不是一样甜呢?
120g
第二杯
20g
60g
第四杯
60g
20÷60
=
1
3
20÷120
=
1
6
60÷60
=1
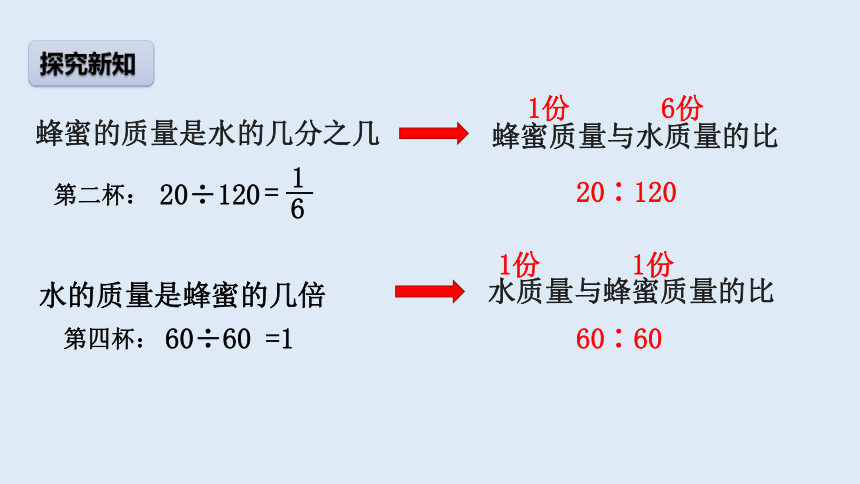
探究新知
水的质量是蜂蜜的几倍
蜂蜜的质量是水的几分之几
20÷120
第二杯:
第四杯:
60÷60
=1
=
1
6
20∶120
60∶60
蜂蜜质量与水质量的比
水质量与蜂蜜质量的比
1份
6份
1份
1份
第一杯
蜂蜜 水
20g
60g
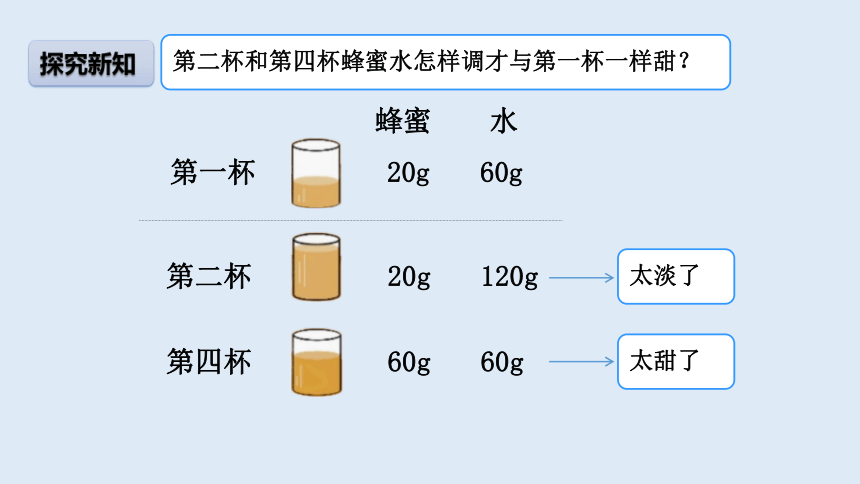
探究新知
第二杯和第四杯蜂蜜水怎样调才与第一杯一样甜?
太淡了
太甜了
120g
第二杯
20g
60g
第四杯
60g
探究新知
探究新知
生活中的比
探究新知
生活中的比
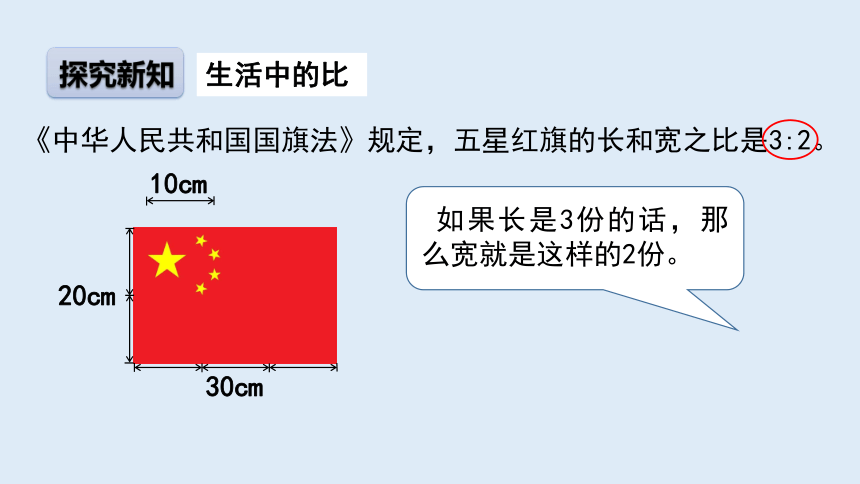
《中华人民共和国国旗法》规定,五星红旗的长和宽之比是3:2。
30cm
20cm
如果长是3份的话,那么宽就是这样的2份。
10cm
探究新知
生活中的比
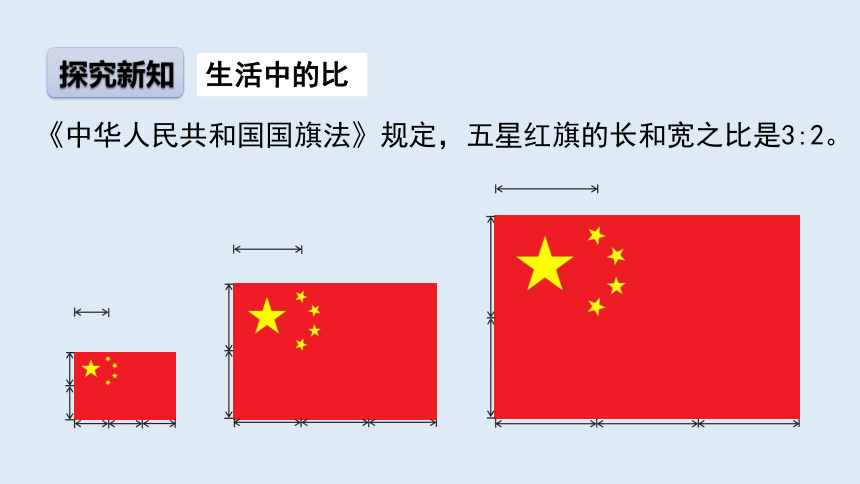
《中华人民共和国国旗法》规定,五星红旗的长和宽之比是3:2。
探究新知
长度的比
小丽喝完蜂蜜水,就去图书馆看书。她离开家,走了5分钟,到了距离家200米的公园,再走3分钟,到了距离公园120米的学校,再走4分钟,到了距离学校160米的图书馆。怎样表示小丽走每段路的速度?
探究新知
你知道哪些数学信息?
家
公园
学校
图书馆
200米
5分钟
120米
3分钟
160米
4分钟
①
②
③
探究新知
① 200 ÷ 5
② 120 ÷ 3
③ 160 ÷ 4
路程 时间
路程∶时间
200 ∶ 5
120 ∶ 3
160 ∶ 4
试用另外两组数学信息列出算式,并写出路程和时间的比。
怎样表示小丽走每段路的速度?
家
公园
学校
图书馆
200米
5分钟
120米
3分钟
160米
4分钟
①
②
③
÷
思考:两个数的比表示什么?
探究新知
思考:两个数的比表示什么?
探究新知
两个数的比表示两个数相除。
你能写出下面的比吗?
(2)一本故事书,小明已经读了87页,还剩132页未读,
已读页数与未读页数的比是( )。
87︰132
(3)一辆汽车走45km用了6L汽油,汽车行驶的路程和耗油
量的比是( )。
45︰6
探究新知
(1)学校开展植树活动,种下的50棵树里有49棵成活了,
成活棵数与种植棵数的比是( )。
49︰50
你学会了什么?
自主学习
数学书第49页
......
......
......
前项
......
比号
后项
比值
15∶10 =
仍读作15比10
......
比还可以写成分数的形式。
怎样求比值?
15 ︰ 10
=15÷10=
自主学习
比的前项除以后项所得的商。
3
2
15
10
比值通常用分数表示,也可以用整数或小数表示。
求比值。
试一试
15︰45
20︰5
0.15︰0.3
= 15÷45=
= 20÷5 = 4
= 0.15÷0.3 = 0.5
1
3
比与除法、分数之间的关系。
比
除法
分数
前项
∶
后项
比值
15
∶
10
=
÷
15
10
=
15
10
=
20
∶
5
=
÷
20
5
=
20
5
=
0.15
∶
0.3
=
÷
0.15
0.3
=
0.15
0.3
=
0.5
4
比一比
3
2
比与除法、分数之间的关系。
比
除法
分数
前项
∶
后项
比值
被除数
除数
商
÷
15
∶
10
=
÷
15
10
=
15
10
=
20
∶
5
=
÷
20
5
=
20
5
=
0.15
∶
0.3
=
÷
0.15
0.3
=
0.15
0.3
=
0.5
4
比一比
3
2
比与除法、分数之间的关系。
比
除法
分数
前项
∶
后项
比值
分子
分母
分数值
被除数
除数
商
÷
15
∶
10
=
÷
15
10
=
15
10
=
20
∶
5
=
÷
20
5
=
20
5
=
0.15
∶
0.3
=
÷
0.15
0.3
=
0.15
0.3
=
0.5
4
比一比
3
2
比与除法、分数之间的关系。
比
除法
分数
前项
∶
后项
比值
分子
分母
分数值
被除数
除数
商
÷
15
∶
10
=
÷
15
10
=
15
10
=
20
∶
5
=
÷
20
5
=
20
5
=
0.15
∶
0.3
=
÷
0.15
0.3
=
0.15
0.3
=
0.5
4
比一比
3
2
注意:比的后项不能为0。
1.填空。
5÷9=( )︰( ) 7÷( )=( )∶12
3∶( )=24 ( )∶8=0.5
5 9
12 7
4
......
被除数
相当于
......
除数
......
商
被除数÷商
3÷24
练一练
1
8
8×0.5
2. 小敏和小亮在文具店买同样的练习本,他们买的数量和总价
如下表:
练一练
总价 数量
小敏 1.8元 6本
小亮 2.4元 8本
② 小亮和小敏花的钱数的比是
( )。
①小敏和小亮买的练习本数量的比是
( )。
③小敏买的练习本的总价和数量的比
是( ),比值是( )。
6∶8
1.8∶6
1.8÷6
2.4∶1.8
这里写1.8∶2.4可以吗?
(改编数学书第49页“做一做”第1题)
0.3
通过这节课的学习,你有哪些收获?
课堂小结
我知道了两个数的比表示两个数相除。
我还学会了如何求比值。
我还知道了比与除法、分数之间的关系。
1.复习数学书第48页至第49页。
课后作业:
2.完成数学书第49页“做一做”第3题和第51页第1题。
六年级上册—人教版—数学—第四单元
比的意义
答疑
答疑
答疑
足球比分2∶0
并不是一个比。
足球比分2∶0是一个比吗?
答疑
足球比分2∶0是一个比吗?
你知道“黄金比”吗?
把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为0.618∶1)。
a
答疑
b
c
a∶b
= b∶c
≈ 0.618∶1
a
b
当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
答疑
a∶b≈0.618∶1
你知道“黄金比”吗?
答疑
你知道“黄金比”吗?
当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
答疑
你知道“黄金比”吗?
a
b
当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
答疑
你知道“黄金比”吗?
a
b
当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
答疑
你知道“黄金比”吗?
当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
谢谢观看!
六年级上册—人教版—数学—第四单元
比的意义
1.经历从具体情境中抽象出比的过程,体会认识比的必要
性,理解比的意义。
2.能正确读写比,会求比值,理解比与除法、分数的关系。3.能利用比的知识解释一些简单的生活问题,感受比在生
活中的广泛应用。
学习目标
情境导入
情境导入
第一杯
蜂蜜 水
20g
60g
120g
第三杯
40g
第二杯
20g
120g
第四杯
60g
60g
为什么蜂蜜和水的质量都变化了,还是一样甜呢?
探究新知
水的质量是蜂蜜的几倍
蜂蜜的质量是水的几分之几
60÷20
20÷60
=
1
3
40÷120
=
1
3
120÷40
3
3
蜂蜜质量与水质量的比
20∶60
40∶120
60∶20
120∶40
比号
水质量与蜂蜜质量的比
1份
3份
1份
3份
...
=
=
第一杯
蜂蜜 水
20g
60g
探究新知
第二杯和第四杯蜂蜜水与第一杯一样甜吗?
太淡了
太甜了
为什么这两杯蜂蜜水与第一杯不是一样甜呢?
120g
第二杯
20g
60g
第四杯
60g
20÷60
=
1
3
20÷120
=
1
6
60÷60
=1
探究新知
水的质量是蜂蜜的几倍
蜂蜜的质量是水的几分之几
20÷120
第二杯:
第四杯:
60÷60
=1
=
1
6
20∶120
60∶60
蜂蜜质量与水质量的比
水质量与蜂蜜质量的比
1份
6份
1份
1份
第一杯
蜂蜜 水
20g
60g
探究新知
第二杯和第四杯蜂蜜水怎样调才与第一杯一样甜?
太淡了
太甜了
120g
第二杯
20g
60g
第四杯
60g
探究新知
探究新知
生活中的比
探究新知
生活中的比
《中华人民共和国国旗法》规定,五星红旗的长和宽之比是3:2。
30cm
20cm
如果长是3份的话,那么宽就是这样的2份。
10cm
探究新知
生活中的比
《中华人民共和国国旗法》规定,五星红旗的长和宽之比是3:2。
探究新知
长度的比
小丽喝完蜂蜜水,就去图书馆看书。她离开家,走了5分钟,到了距离家200米的公园,再走3分钟,到了距离公园120米的学校,再走4分钟,到了距离学校160米的图书馆。怎样表示小丽走每段路的速度?
探究新知
你知道哪些数学信息?
家
公园
学校
图书馆
200米
5分钟
120米
3分钟
160米
4分钟
①
②
③
探究新知
① 200 ÷ 5
② 120 ÷ 3
③ 160 ÷ 4
路程 时间
路程∶时间
200 ∶ 5
120 ∶ 3
160 ∶ 4
试用另外两组数学信息列出算式,并写出路程和时间的比。
怎样表示小丽走每段路的速度?
家
公园
学校
图书馆
200米
5分钟
120米
3分钟
160米
4分钟
①
②
③
÷
思考:两个数的比表示什么?
探究新知
思考:两个数的比表示什么?
探究新知
两个数的比表示两个数相除。
你能写出下面的比吗?
(2)一本故事书,小明已经读了87页,还剩132页未读,
已读页数与未读页数的比是( )。
87︰132
(3)一辆汽车走45km用了6L汽油,汽车行驶的路程和耗油
量的比是( )。
45︰6
探究新知
(1)学校开展植树活动,种下的50棵树里有49棵成活了,
成活棵数与种植棵数的比是( )。
49︰50
你学会了什么?
自主学习
数学书第49页
......
......
......
前项
......
比号
后项
比值
15∶10 =
仍读作15比10
......
比还可以写成分数的形式。
怎样求比值?
15 ︰ 10
=15÷10=
自主学习
比的前项除以后项所得的商。
3
2
15
10
比值通常用分数表示,也可以用整数或小数表示。
求比值。
试一试
15︰45
20︰5
0.15︰0.3
= 15÷45=
= 20÷5 = 4
= 0.15÷0.3 = 0.5
1
3
比与除法、分数之间的关系。
比
除法
分数
前项
∶
后项
比值
15
∶
10
=
÷
15
10
=
15
10
=
20
∶
5
=
÷
20
5
=
20
5
=
0.15
∶
0.3
=
÷
0.15
0.3
=
0.15
0.3
=
0.5
4
比一比
3
2
比与除法、分数之间的关系。
比
除法
分数
前项
∶
后项
比值
被除数
除数
商
÷
15
∶
10
=
÷
15
10
=
15
10
=
20
∶
5
=
÷
20
5
=
20
5
=
0.15
∶
0.3
=
÷
0.15
0.3
=
0.15
0.3
=
0.5
4
比一比
3
2
比与除法、分数之间的关系。
比
除法
分数
前项
∶
后项
比值
分子
分母
分数值
被除数
除数
商
÷
15
∶
10
=
÷
15
10
=
15
10
=
20
∶
5
=
÷
20
5
=
20
5
=
0.15
∶
0.3
=
÷
0.15
0.3
=
0.15
0.3
=
0.5
4
比一比
3
2
比与除法、分数之间的关系。
比
除法
分数
前项
∶
后项
比值
分子
分母
分数值
被除数
除数
商
÷
15
∶
10
=
÷
15
10
=
15
10
=
20
∶
5
=
÷
20
5
=
20
5
=
0.15
∶
0.3
=
÷
0.15
0.3
=
0.15
0.3
=
0.5
4
比一比
3
2
注意:比的后项不能为0。
1.填空。
5÷9=( )︰( ) 7÷( )=( )∶12
3∶( )=24 ( )∶8=0.5
5 9
12 7
4
......
被除数
相当于
......
除数
......
商
被除数÷商
3÷24
练一练
1
8
8×0.5
2. 小敏和小亮在文具店买同样的练习本,他们买的数量和总价
如下表:
练一练
总价 数量
小敏 1.8元 6本
小亮 2.4元 8本
② 小亮和小敏花的钱数的比是
( )。
①小敏和小亮买的练习本数量的比是
( )。
③小敏买的练习本的总价和数量的比
是( ),比值是( )。
6∶8
1.8∶6
1.8÷6
2.4∶1.8
这里写1.8∶2.4可以吗?
(改编数学书第49页“做一做”第1题)
0.3
通过这节课的学习,你有哪些收获?
课堂小结
我知道了两个数的比表示两个数相除。
我还学会了如何求比值。
我还知道了比与除法、分数之间的关系。
1.复习数学书第48页至第49页。
课后作业:
2.完成数学书第49页“做一做”第3题和第51页第1题。
六年级上册—人教版—数学—第四单元
比的意义
答疑
答疑
答疑
足球比分2∶0
并不是一个比。
足球比分2∶0是一个比吗?
答疑
足球比分2∶0是一个比吗?
你知道“黄金比”吗?
把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为0.618∶1)。
a
答疑
b
c
a∶b
= b∶c
≈ 0.618∶1
a
b
当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
答疑
a∶b≈0.618∶1
你知道“黄金比”吗?
答疑
你知道“黄金比”吗?
当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
答疑
你知道“黄金比”吗?
a
b
当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
答疑
你知道“黄金比”吗?
a
b
当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
答疑
你知道“黄金比”吗?
当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
谢谢观看!
