人教A版(2019)必修第一册1.1集合的概念 课件(共22张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册1.1集合的概念 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 14:29:00 | ||
图片预览








文档简介
(共22张PPT)
1.1集合的概念
第一章 集合与常用逻辑用语
结构导图
导
01
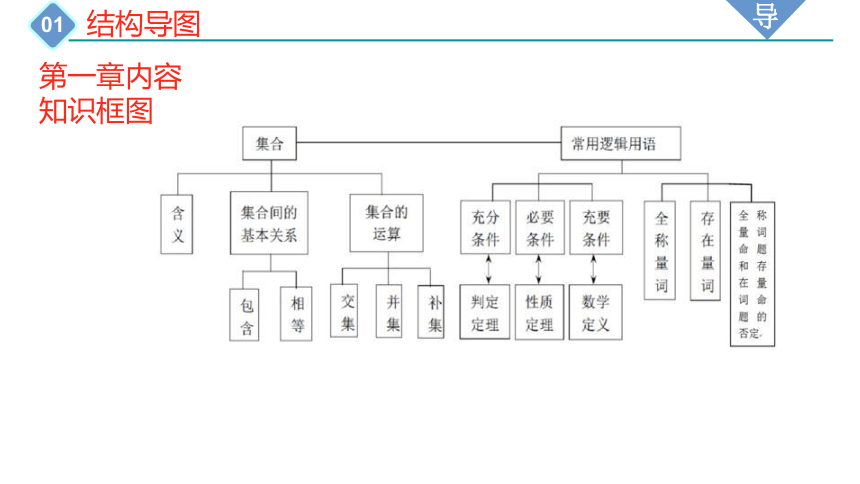
第一章内容
知识框图
情景1:“集合”是日常生活中的一个常用词,现代汉语解释为: 许多的人或物聚在一起.
在现代数学中,集合是一种简洁、高雅的数学语言,是一种工具。集合的知识是现代数学的基础。
康托尔(G.Cantor,1845-1918).德国数学家,集合论创始人.人们把康托尔于1873年12月7日给戴德金的信中最早提出集合论思想的那一天定为集合论诞生日.
问题情境
引
02
我们怎样理解数学中的“集合”?
引
02
(1)通过实例,了解元素及集合的含义,理解元素与集合的“属于”关系;
(2)了解集合相等的含义,了解集合中元素的确定性、互异性、无序性;
(3)知道常用数集及其专用记号;
(4)针对具体问题,能在自然语言基础上,用列举法和描述法刻画集合,从中感受集合语言的意义和作用,提升数学抽象素养。
达成上述目标的标志是:
(1)能结合具体实例认识和识别,知道什么是集合。对于给出的一些例子,会判断哪些事物可以组成集合,哪些不能组成集合。
(2)知道两个集合相等应满足的条件。结合具体情境,判断元素与集合的关系,体会集合中元素的确定性、互异性、无序性。
(3)知道常用数集及其记法,会用这些表示法表示常用数集。
(4)对于给定的具体情境,抽象概括出数学对象的一般特征,会用自然语言、符号语言(列举法和描述法)表达所要研究的数学对象,并能根据需求进行转换,从中感受集合语言的意义和作用,积累数学抽象经验。
初中,我们已经接触过一些集合:
1.将下列数字填入相应的集合:
自然数集合
有理数集合
2.圆的定义:平面内到定点的距离等于定长的点的集合.
引
02
考察下列问题: (1)1~20以内的所有偶数;
(2)立德中学今年入学的全体高一学生;
(3)所有正方形;
(4)到直线l的距离等于定长d的所有的点;
(5)方程 的所有实数根;
(6)地球上的四大洋。
思考:
上述每个问题都由若干个对象组成,每组对象的全体都能组成集合吗?我们把研究的对象统称为元素,它们的元素分别是什么?
思
03
你对集合的理解?
1.是一定范围内确定的对象;
2.是不同的对象;
3.是这些对象的全体.
建构新知
一般地, 我们把研究对象统称为元素. 通常用小写拉丁字母a,b,c,...来表示.我们把一些元素组成的总体叫做集合(简称为集). 通常用大写拉丁字母A,B,C,...来表示.
组成集合的元素可以是哪些类型?
组成集合的元素类型可以是:物、数、图、点(有序实数对)等,那元素它又具备怎样的性质呢?
追问:
1. 元素、集合
评
03
思考:我们研究一个新概念的一般思路是什么?
概念—特性—表示—应用
1) 所有的“帅哥”能否构成一个集合?由此说明什么?
评
03
2) 由1, 3, 0, 5, ︱-3 ︳这些数组成的一个集合中有5个元素,这种说法正确吗?
3)高一(5)班的全体同学组成一个集合,调整座位后这个集合有没有变化?
2. 集合中元素的特征
确定性、互异性、无序性
通过以上的学习你能说出集合中元素的特征吗?
建构新知
追问:类比实数相等,两个集合相等应满足什么条件?
练习 1.判断以下元素的全体是否组成集合,如果是请说出其中的元素。
(1) 大于3小于11的偶数; (2) 我国的小河流. (3)单词“”中的字母
解:(1)是由4,6,8,10四个元素组成的集合.
(2)由集合元素的确定性知其不能组成集合.
(3) s e t
03
你能举出集合的例子吗?
两个集合相等应满足的条件:两个集合的元素是一样的。
建构新知
2.已知下面的两个实例:
(1)用A表示高一(3)班全体学生组成的集合.
(2)用a表示高一(3)班的一位同学,b 表示高一(4)班的一位同学.
a是集合A中的元素,b不是集合A中的元素.
如何用符号表示a,b与集合A之间的关系
03
3.元素a与集合A的关系
如果a是集合A的元素,就说a属于集合A,记作a∈A ;
如果a不是集合A中的元素,就说a不属于集合A,记作a A.
常用的数集 自然数集 正整数集 整数集 有理数集 实数集
记法 —— ———— —— —— ——
Q
R
N
Z
N*或N+
学习集合与元素的概念后,为了方便书写,数学中规定了一些常用数集及其记法:
03
练习2. 用符号“∈”或“ ”填空.
(1)2 N.
(2) ____________Q.
(3)0 {0}.
(4)b {a,b,c}.
思考1:地球上的四大洋组成的集合如何表示?
{太平洋,大西洋,印度洋,北冰洋}.
探究2. 集合的表示方法
2: 方程(x+1)(x+2)=0的所有根组成的集合又如何用列举法表示呢?
【提示】 {-1,-2}
列举法
评
03
列举法
把集合的元素一一列举出来,并用花括号“{ }” 括起来表示集合的方法叫做列举法.
注意:
元素间要用逗号隔开.
大括号不能缺失
a与{a}有什么区别?
是一个元素
是一个集合
例1. 用列举法表示下列集合:
(1)小于10的所有自然数组成的集合.
(2)方程x2=x的所有实数根组成的集合.
解:(1)设小于10的所有自然数组成的集合为A, 那么 A={0,1,2,3,4,5,6,7,8,9}.
(2)设方程x2=x的所有实数根组成的集合为B,那么 B={1,0}.
巩固应用
评
04
也可以表示为A={9,8,7,6,5,4,3,2,1,0}
思考:1)你能用自然语言描述集合{0,3,6,9}吗?
2)能否用列举法表示不等式 x-3<7的解集?
由于小于10的实数有无穷多个,而且无法一一列举出来, 因此这个集合不能用列举法表示.但是可以看出,这个集合中的元素满足性质:
(1) 集合中的元素都小于10.
(2) 集合中的元素都是实数.
这个集合可以通过描述其元素性质的方法来表示,
写作:
描述法
思考:1)你能用自然语言描述集合{0,3,6,9}吗?
2)能否用列举法表示不等式 x-3<7的解集?
评
03
巩固应用
我们可以把奇数集合表示为
又如所有偶数的集合怎样表示?
x=2k ,
k∈Z
x∈Z
|
{ }
还可以把奇数集合表示为
评
04
注:如果从上下文的关系来看, x∈R ,x∈Z
是明确的,那么x∈R ,x∈Z 可以省略,只写元素x.
例如. { x∈R | x<10 }
= { x | x<10 }
{ x∈Z | x=2k, k∈Z}
= { x | x=2k, k∈Z}
巩固应用
例2. 试分别用列举法和描述法表示下列集合.
(1)方程x2-2=0的所有实数根组成的集合.
(2)由大于10小于20的所有整数组成的集合.
方程x2-2=0有两个实数根为 ,因此,用列举法表示为A={ }.
解:(1)设方程x2-2=0的实数根为x,并且满足条件
x2-2=0,因此,用描述法表示为A={x∈R|x2-2=0}.
评
04
用列举法表示为
B={x∈Z∣10B={11,12,13,14,15,16,17,18,19}.
(2)设大于10小于20的整数为x,它满足条件x∈Z,且10巩固应用
思考:你能说出列举法和描述法的优缺点吗?
优点 缺点
列举法 直观、明了 不易看出元素所具有的属性,且有些集合不能用列举法表示
描述法 把集合中元素所具有的性质描述出来,具有抽象性、概括性、普遍性的特点 不易看出集合的具体元素
评
04
今天学习了哪些新知识?新方法?
1.集合的概念;
2.集合元素的性质:确定性,互异性,无序性;
3.数集及有关符号;
4. 集合的表示方法.
5. 元素与集合的关系.。
结
05
课堂总结
学完了集合的含义、接下来我们将要学习什么呢?
结
05
结构再望
集合之间的关系
达标检测
评
05
达标检测
评
05
达标检测
评
05
解题方法(认识集合含义的2个步骤)
1.1集合的概念
第一章 集合与常用逻辑用语
结构导图
导
01
第一章内容
知识框图
情景1:“集合”是日常生活中的一个常用词,现代汉语解释为: 许多的人或物聚在一起.
在现代数学中,集合是一种简洁、高雅的数学语言,是一种工具。集合的知识是现代数学的基础。
康托尔(G.Cantor,1845-1918).德国数学家,集合论创始人.人们把康托尔于1873年12月7日给戴德金的信中最早提出集合论思想的那一天定为集合论诞生日.
问题情境
引
02
我们怎样理解数学中的“集合”?
引
02
(1)通过实例,了解元素及集合的含义,理解元素与集合的“属于”关系;
(2)了解集合相等的含义,了解集合中元素的确定性、互异性、无序性;
(3)知道常用数集及其专用记号;
(4)针对具体问题,能在自然语言基础上,用列举法和描述法刻画集合,从中感受集合语言的意义和作用,提升数学抽象素养。
达成上述目标的标志是:
(1)能结合具体实例认识和识别,知道什么是集合。对于给出的一些例子,会判断哪些事物可以组成集合,哪些不能组成集合。
(2)知道两个集合相等应满足的条件。结合具体情境,判断元素与集合的关系,体会集合中元素的确定性、互异性、无序性。
(3)知道常用数集及其记法,会用这些表示法表示常用数集。
(4)对于给定的具体情境,抽象概括出数学对象的一般特征,会用自然语言、符号语言(列举法和描述法)表达所要研究的数学对象,并能根据需求进行转换,从中感受集合语言的意义和作用,积累数学抽象经验。
初中,我们已经接触过一些集合:
1.将下列数字填入相应的集合:
自然数集合
有理数集合
2.圆的定义:平面内到定点的距离等于定长的点的集合.
引
02
考察下列问题: (1)1~20以内的所有偶数;
(2)立德中学今年入学的全体高一学生;
(3)所有正方形;
(4)到直线l的距离等于定长d的所有的点;
(5)方程 的所有实数根;
(6)地球上的四大洋。
思考:
上述每个问题都由若干个对象组成,每组对象的全体都能组成集合吗?我们把研究的对象统称为元素,它们的元素分别是什么?
思
03
你对集合的理解?
1.是一定范围内确定的对象;
2.是不同的对象;
3.是这些对象的全体.
建构新知
一般地, 我们把研究对象统称为元素. 通常用小写拉丁字母a,b,c,...来表示.我们把一些元素组成的总体叫做集合(简称为集). 通常用大写拉丁字母A,B,C,...来表示.
组成集合的元素可以是哪些类型?
组成集合的元素类型可以是:物、数、图、点(有序实数对)等,那元素它又具备怎样的性质呢?
追问:
1. 元素、集合
评
03
思考:我们研究一个新概念的一般思路是什么?
概念—特性—表示—应用
1) 所有的“帅哥”能否构成一个集合?由此说明什么?
评
03
2) 由1, 3, 0, 5, ︱-3 ︳这些数组成的一个集合中有5个元素,这种说法正确吗?
3)高一(5)班的全体同学组成一个集合,调整座位后这个集合有没有变化?
2. 集合中元素的特征
确定性、互异性、无序性
通过以上的学习你能说出集合中元素的特征吗?
建构新知
追问:类比实数相等,两个集合相等应满足什么条件?
练习 1.判断以下元素的全体是否组成集合,如果是请说出其中的元素。
(1) 大于3小于11的偶数; (2) 我国的小河流. (3)单词“”中的字母
解:(1)是由4,6,8,10四个元素组成的集合.
(2)由集合元素的确定性知其不能组成集合.
(3) s e t
03
你能举出集合的例子吗?
两个集合相等应满足的条件:两个集合的元素是一样的。
建构新知
2.已知下面的两个实例:
(1)用A表示高一(3)班全体学生组成的集合.
(2)用a表示高一(3)班的一位同学,b 表示高一(4)班的一位同学.
a是集合A中的元素,b不是集合A中的元素.
如何用符号表示a,b与集合A之间的关系
03
3.元素a与集合A的关系
如果a是集合A的元素,就说a属于集合A,记作a∈A ;
如果a不是集合A中的元素,就说a不属于集合A,记作a A.
常用的数集 自然数集 正整数集 整数集 有理数集 实数集
记法 —— ———— —— —— ——
Q
R
N
Z
N*或N+
学习集合与元素的概念后,为了方便书写,数学中规定了一些常用数集及其记法:
03
练习2. 用符号“∈”或“ ”填空.
(1)2 N.
(2) ____________Q.
(3)0 {0}.
(4)b {a,b,c}.
思考1:地球上的四大洋组成的集合如何表示?
{太平洋,大西洋,印度洋,北冰洋}.
探究2. 集合的表示方法
2: 方程(x+1)(x+2)=0的所有根组成的集合又如何用列举法表示呢?
【提示】 {-1,-2}
列举法
评
03
列举法
把集合的元素一一列举出来,并用花括号“{ }” 括起来表示集合的方法叫做列举法.
注意:
元素间要用逗号隔开.
大括号不能缺失
a与{a}有什么区别?
是一个元素
是一个集合
例1. 用列举法表示下列集合:
(1)小于10的所有自然数组成的集合.
(2)方程x2=x的所有实数根组成的集合.
解:(1)设小于10的所有自然数组成的集合为A, 那么 A={0,1,2,3,4,5,6,7,8,9}.
(2)设方程x2=x的所有实数根组成的集合为B,那么 B={1,0}.
巩固应用
评
04
也可以表示为A={9,8,7,6,5,4,3,2,1,0}
思考:1)你能用自然语言描述集合{0,3,6,9}吗?
2)能否用列举法表示不等式 x-3<7的解集?
由于小于10的实数有无穷多个,而且无法一一列举出来, 因此这个集合不能用列举法表示.但是可以看出,这个集合中的元素满足性质:
(1) 集合中的元素都小于10.
(2) 集合中的元素都是实数.
这个集合可以通过描述其元素性质的方法来表示,
写作:
描述法
思考:1)你能用自然语言描述集合{0,3,6,9}吗?
2)能否用列举法表示不等式 x-3<7的解集?
评
03
巩固应用
我们可以把奇数集合表示为
又如所有偶数的集合怎样表示?
x=2k ,
k∈Z
x∈Z
|
{ }
还可以把奇数集合表示为
评
04
注:如果从上下文的关系来看, x∈R ,x∈Z
是明确的,那么x∈R ,x∈Z 可以省略,只写元素x.
例如. { x∈R | x<10 }
= { x | x<10 }
{ x∈Z | x=2k, k∈Z}
= { x | x=2k, k∈Z}
巩固应用
例2. 试分别用列举法和描述法表示下列集合.
(1)方程x2-2=0的所有实数根组成的集合.
(2)由大于10小于20的所有整数组成的集合.
方程x2-2=0有两个实数根为 ,因此,用列举法表示为A={ }.
解:(1)设方程x2-2=0的实数根为x,并且满足条件
x2-2=0,因此,用描述法表示为A={x∈R|x2-2=0}.
评
04
用列举法表示为
B={x∈Z∣10
(2)设大于10小于20的整数为x,它满足条件x∈Z,且10
思考:你能说出列举法和描述法的优缺点吗?
优点 缺点
列举法 直观、明了 不易看出元素所具有的属性,且有些集合不能用列举法表示
描述法 把集合中元素所具有的性质描述出来,具有抽象性、概括性、普遍性的特点 不易看出集合的具体元素
评
04
今天学习了哪些新知识?新方法?
1.集合的概念;
2.集合元素的性质:确定性,互异性,无序性;
3.数集及有关符号;
4. 集合的表示方法.
5. 元素与集合的关系.。
结
05
课堂总结
学完了集合的含义、接下来我们将要学习什么呢?
结
05
结构再望
集合之间的关系
达标检测
评
05
达标检测
评
05
达标检测
评
05
解题方法(认识集合含义的2个步骤)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
