人教版六年级数学上册 圆环的面积(例2) 课件(共29张PPT)
文档属性
| 名称 | 人教版六年级数学上册 圆环的面积(例2) 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 15:30:45 | ||
图片预览





文档简介
(共29张PPT)
圆环的面积(例2)
六年级上册—人教版—数学—第五单元
1. 认识圆环的特征,掌握计算圆环的方法,并能准确计算圆环的面积。
2. 通过自主探究,培养独立思考的意识。
3. 在解决实际问题的过程中,进一步体验图形和生活的联系,提高学习数学的兴趣。
学习目标
生活中的圆环……
动手操作:在练习本上用圆规画一个
任意大小的圆环。
O
同心圆
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
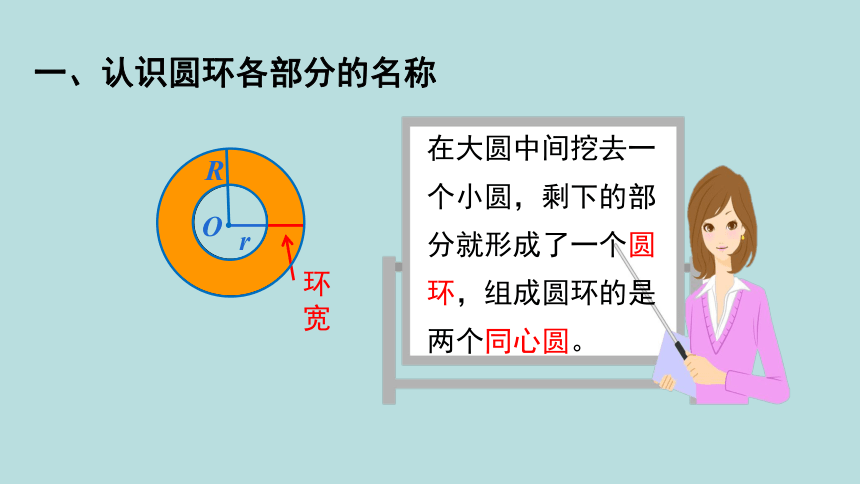
r
R
环宽
O
一、认识圆环各部分的名称
同心圆
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
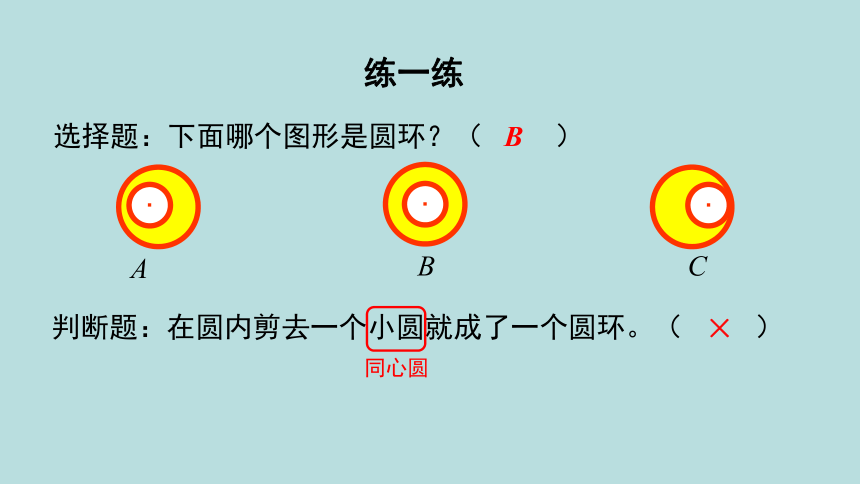
选择题:下面哪个图形是圆环?( )
·
·
·
A
B
C
练一练
B
判断题:在圆内剪去一个小圆就成了一个圆环。( )
×
同心圆
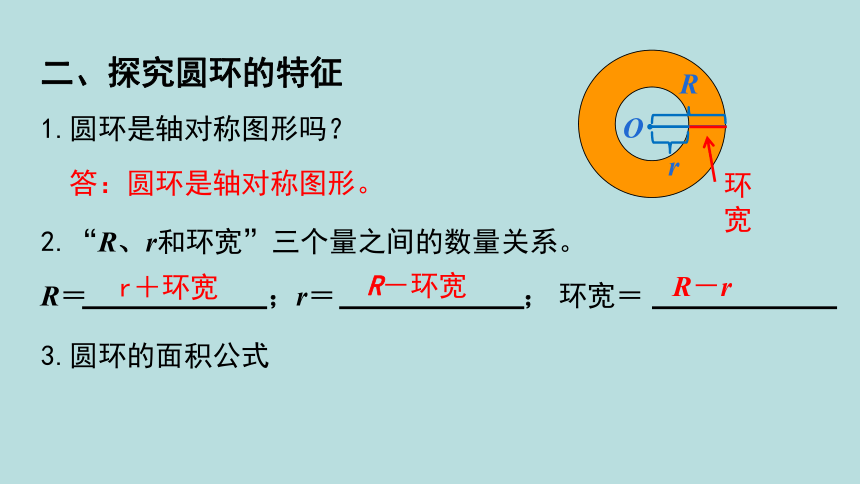
二、探究圆环的特征
1.圆环是轴对称图形吗?
2.“R、r和环宽”三个量之间的数量关系。
3.圆环的面积公式
R= ;r= ; 环宽=
r+环宽
答:圆环是轴对称图形。
r
R
环宽
O
R-环宽
R-r
二、探究圆环的特征
1.圆环是轴对称图形吗?
2.“R、r和环宽”三个量之间的数量关系。
3.圆环的面积公式
R= ;r= ; 环宽=
S圆环= π(R - r )
S圆环= S大圆 - S小圆
r+环宽
R-环宽
R-r
答:圆环是轴对称图形。
S圆环= πR - πr
①
②
三、圆环面积公式的应用
例2(数学书第68页)
光盘的银色部分是一个圆环,内圆半径是2cm,
外圆半径是6cm。它的面积是多少?
R=6cm
r=2cm
你知道了哪些信息?
信息①:内圆的半径是( )cm;
信息②:外圆的半径是( )cm。
问 题:( ) 是多少。
6
2
圆环的面积
三、圆环面积公式的应用
例2(数学书第68页)
光盘的银色部分是一个圆环,内圆半径是2cm,
外圆半径是6cm。它的面积是多少?
R=6cm
r=2cm
S圆环= πR - πr
= 3.14×6 - 3.14×2
= 3.14×36- 3.14×4
= 113.04- 12.56
= 100.48(cm )
S圆环= π(R - r )
=3.14×(6 - 2 )
=3.14×32
=100.48(cm )
答:它的面积是100.48cm 。
S圆环= π(R - r )
R, r
归纳总结
练一练
1.填空题:
(1)一个圆形环岛的直径是50 m,中间是一个直径为10 m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
已知直径,先求( )。
R=( )m,r=( )m。
求圆环的面积,只列式不计算:
圆的半径
25
5
3.14×(25 -5 )
解题思路:
S圆环= π(R - r )
R, r
归纳总结
d
r= d÷2
练一练
1.填空题:
(2)圆环的外圆周长为31.4分米,内圆周长为12.56分米,求圆环面积。
已知周长,先求( )。
R=( )dm,r=( )dm。
求圆环的面积,只列式不计算:
圆的半径
5
2
3.14×(5 -2 )
解题思路:
S圆环= π(R - r )
R, r
归纳总结
d
r= d÷2
C
r= C÷ π ÷2
练一练
2.认真观察下图,根据给出的数据求出圆环的面积。
8cm
6cm
2cm
3cm
4cm
O
O
O
S圆环= π(R - r )
=3.14×(6 - 4 )
=3.14×20
=62.8(cm )
R=6cm;环宽=2cm
r=6 - 2=4(cm)
S圆环= π(R - r )
=3.14×(7 - 3 )
=3.14×40
=125.6(cm )
r=3cm;环宽=4cm
R=3+4=7(cm)
只知道大圆的直径,
无法求圆环的面积。
小圆的半径
小圆的直径
小圆的周长
环宽
……
S圆环= π(R - r )
R, r
归纳总结
d
r= d÷2
C
r= C÷ π ÷2
环宽
其中一个圆的半径
练一练
3.已知图中大正方形的面积是36平方厘米,
小正方形的面积是4平方厘米,求圆环的
面积。
O
R
r
S圆环= π(R - r )
=3.14×(36 - 4)
=3.14×32
=100.48(cm )
答:圆环的面积是100.48cm 。
R =36cm
r =4cm
S圆环= π(R - r )
R, r
归纳总结
d
r= d÷2
C
r= C÷ π ÷2
环宽
其中一个圆的半径
R
r
课堂小结
圆环各部分的名称:
圆环的特征:
圆环的面积公式:
R=r+环宽
r=R-环宽
环宽=R-r
S圆环= πR - πr
S圆环= π(R - r )
R
R, r
d, C
环宽
r
乘法分配律
r
R
环宽
O
课后作业
1.复习本节课内容(数学书第68页例2)。
2.数学书第72页第5、6、7题。
圆环的面积(答疑)
六年级上册—人教版—数学—第五单元
答 疑
①
②
S圆环= π(R - r )
=3.14×(3 - 1 )
=3.14×8
=25.12(m )
答 疑
有一个半径为3米的圆形花坛,周围有一条宽1米的环形小路,
这条小路的面积是多少平方米?
答:这条小路的面积是25.12m 。
答 疑
有一个半径为3米的圆形花坛,周围有一条宽1米的环形小路,
这条小路的面积是多少平方米?
3m
1m
答:这条小路的面积是21.98m 。
r=3m;环宽=1m
R=3+1=4(m)
S圆环= π(R - r )
=3.14×(4 - 3 )
=3.14×7
=21.98(m )
O
R
r
S圆环 = π(R - r )
=3.14×9
=28.26(cm )
答:圆环的面积是28.26cm 。
S大正方形= R
S小正方形= r
答 疑
已知图中阴影部分的面积是9平方厘米,
求圆环的面积。
S阴影= R - r =9(cm )
谢谢观看!
圆环的面积(例2)
六年级上册—人教版—数学—第五单元
1. 认识圆环的特征,掌握计算圆环的方法,并能准确计算圆环的面积。
2. 通过自主探究,培养独立思考的意识。
3. 在解决实际问题的过程中,进一步体验图形和生活的联系,提高学习数学的兴趣。
学习目标
生活中的圆环……
动手操作:在练习本上用圆规画一个
任意大小的圆环。
O
同心圆
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
r
R
环宽
O
一、认识圆环各部分的名称
同心圆
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
选择题:下面哪个图形是圆环?( )
·
·
·
A
B
C
练一练
B
判断题:在圆内剪去一个小圆就成了一个圆环。( )
×
同心圆
二、探究圆环的特征
1.圆环是轴对称图形吗?
2.“R、r和环宽”三个量之间的数量关系。
3.圆环的面积公式
R= ;r= ; 环宽=
r+环宽
答:圆环是轴对称图形。
r
R
环宽
O
R-环宽
R-r
二、探究圆环的特征
1.圆环是轴对称图形吗?
2.“R、r和环宽”三个量之间的数量关系。
3.圆环的面积公式
R= ;r= ; 环宽=
S圆环= π(R - r )
S圆环= S大圆 - S小圆
r+环宽
R-环宽
R-r
答:圆环是轴对称图形。
S圆环= πR - πr
①
②
三、圆环面积公式的应用
例2(数学书第68页)
光盘的银色部分是一个圆环,内圆半径是2cm,
外圆半径是6cm。它的面积是多少?
R=6cm
r=2cm
你知道了哪些信息?
信息①:内圆的半径是( )cm;
信息②:外圆的半径是( )cm。
问 题:( ) 是多少。
6
2
圆环的面积
三、圆环面积公式的应用
例2(数学书第68页)
光盘的银色部分是一个圆环,内圆半径是2cm,
外圆半径是6cm。它的面积是多少?
R=6cm
r=2cm
S圆环= πR - πr
= 3.14×6 - 3.14×2
= 3.14×36- 3.14×4
= 113.04- 12.56
= 100.48(cm )
S圆环= π(R - r )
=3.14×(6 - 2 )
=3.14×32
=100.48(cm )
答:它的面积是100.48cm 。
S圆环= π(R - r )
R, r
归纳总结
练一练
1.填空题:
(1)一个圆形环岛的直径是50 m,中间是一个直径为10 m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
已知直径,先求( )。
R=( )m,r=( )m。
求圆环的面积,只列式不计算:
圆的半径
25
5
3.14×(25 -5 )
解题思路:
S圆环= π(R - r )
R, r
归纳总结
d
r= d÷2
练一练
1.填空题:
(2)圆环的外圆周长为31.4分米,内圆周长为12.56分米,求圆环面积。
已知周长,先求( )。
R=( )dm,r=( )dm。
求圆环的面积,只列式不计算:
圆的半径
5
2
3.14×(5 -2 )
解题思路:
S圆环= π(R - r )
R, r
归纳总结
d
r= d÷2
C
r= C÷ π ÷2
练一练
2.认真观察下图,根据给出的数据求出圆环的面积。
8cm
6cm
2cm
3cm
4cm
O
O
O
S圆环= π(R - r )
=3.14×(6 - 4 )
=3.14×20
=62.8(cm )
R=6cm;环宽=2cm
r=6 - 2=4(cm)
S圆环= π(R - r )
=3.14×(7 - 3 )
=3.14×40
=125.6(cm )
r=3cm;环宽=4cm
R=3+4=7(cm)
只知道大圆的直径,
无法求圆环的面积。
小圆的半径
小圆的直径
小圆的周长
环宽
……
S圆环= π(R - r )
R, r
归纳总结
d
r= d÷2
C
r= C÷ π ÷2
环宽
其中一个圆的半径
练一练
3.已知图中大正方形的面积是36平方厘米,
小正方形的面积是4平方厘米,求圆环的
面积。
O
R
r
S圆环= π(R - r )
=3.14×(36 - 4)
=3.14×32
=100.48(cm )
答:圆环的面积是100.48cm 。
R =36cm
r =4cm
S圆环= π(R - r )
R, r
归纳总结
d
r= d÷2
C
r= C÷ π ÷2
环宽
其中一个圆的半径
R
r
课堂小结
圆环各部分的名称:
圆环的特征:
圆环的面积公式:
R=r+环宽
r=R-环宽
环宽=R-r
S圆环= πR - πr
S圆环= π(R - r )
R
R, r
d, C
环宽
r
乘法分配律
r
R
环宽
O
课后作业
1.复习本节课内容(数学书第68页例2)。
2.数学书第72页第5、6、7题。
圆环的面积(答疑)
六年级上册—人教版—数学—第五单元
答 疑
①
②
S圆环= π(R - r )
=3.14×(3 - 1 )
=3.14×8
=25.12(m )
答 疑
有一个半径为3米的圆形花坛,周围有一条宽1米的环形小路,
这条小路的面积是多少平方米?
答:这条小路的面积是25.12m 。
答 疑
有一个半径为3米的圆形花坛,周围有一条宽1米的环形小路,
这条小路的面积是多少平方米?
3m
1m
答:这条小路的面积是21.98m 。
r=3m;环宽=1m
R=3+1=4(m)
S圆环= π(R - r )
=3.14×(4 - 3 )
=3.14×7
=21.98(m )
O
R
r
S圆环 = π(R - r )
=3.14×9
=28.26(cm )
答:圆环的面积是28.26cm 。
S大正方形= R
S小正方形= r
答 疑
已知图中阴影部分的面积是9平方厘米,
求圆环的面积。
S阴影= R - r =9(cm )
谢谢观看!
