人教版六年级数学上册 圆的面积综合练习课 课件(共41张PPT)
文档属性
| 名称 | 人教版六年级数学上册 圆的面积综合练习课 课件(共41张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 15:15:49 | ||
图片预览







文档简介
(共41张PPT)
六年级—人教版—数学—第五单元
圆的面积综合练习课
1.理解与掌握圆的面积计算公式,并据此解决一些简单的实际问题。
2.体验与理解通过赋值法和代数法解决实际问题的解题思路。
3.沟通知识点间的内在联系,进一步体会和理解转化的数学思想与方法。
学习目标
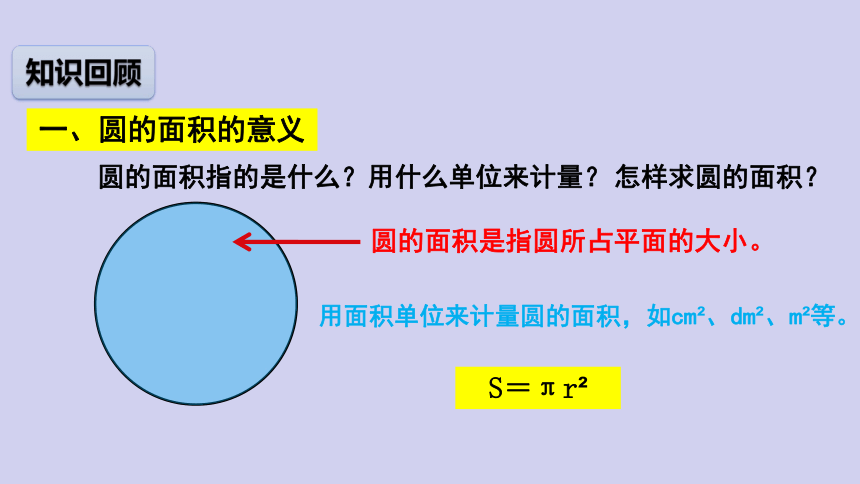
圆的面积指的是什么?用什么单位来计量?
圆的面积是指圆所占平面的大小。
用面积单位来计量圆的面积,如cm 、dm 、m 等。
一、圆的面积的意义
知识回顾
S=πr
怎样求圆的面积?
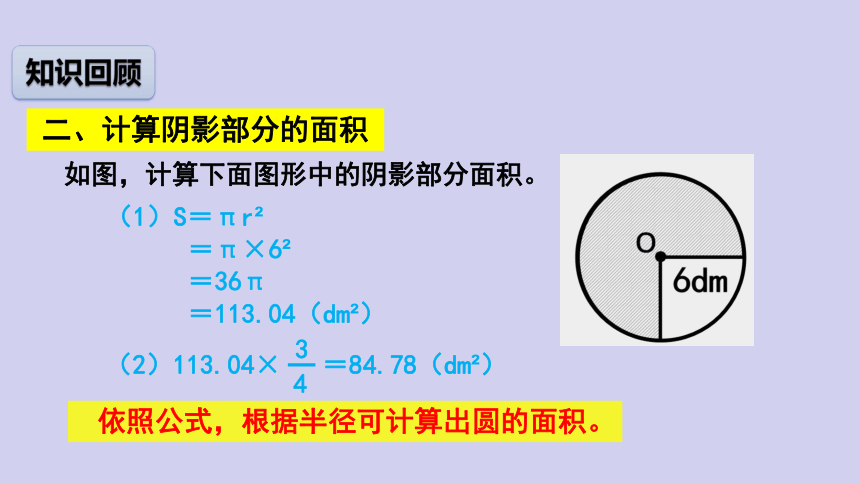
如图,计算下面图形中的阴影部分面积。
(1)S=πr
=π×6
=36π
=113.04(dm )
二、计算阴影部分的面积
知识回顾
(2)113.04× =84.78(dm )
4
3
依照公式,根据半径可计算出圆的面积。
1.如图,如果正方形的面积是100cm ,那么圆的面积是多少cm ?
三、灵活求圆的面积
知识回顾
由r×r=100,可知r =100,
根据S=πr ,可知
圆的面积是:S=πr =π×100=100π=314(cm )
由r×r=100,可知r=10,
根据S=πr ,可知
圆的面积是:S=πr =π×10 =100π=314(cm )
解法一
解法二
2.如图,如果正方形的面积是10cm ,那么圆的面积是多少cm ?
三、灵活求圆的面积
知识回顾
由r×r=10,可知r =10,
根据S=πr ,可知
圆的面积是:S=πr =π×10=10π=31.4(cm )
3.如图,如果三角形的面积是15cm ,那么圆的面积是多少cm ?
三、灵活求圆的面积
知识回顾
由r×r÷2=15,可知r =30,
根据S=πr ,可知
圆的面积是:S=πr =π×30=30π=94.2(cm )
根据公式,可推算出圆的面积。
如图,若半圆形的周长是30.84cm,则半圆形的面积是多少cm ?
四、求半圆形的面积
知识回顾
(1)解:设这个圆的半径是rcm。
πr+2r=30.84
(π+2 )r=30.84
5.14r=30.84
r=30.84÷5.14
r=6
(2)S半=πr ÷2
=π×6 ÷2
=36π÷2
=18π
=56.52(cm )
逆向运用公式求出圆的半径后,再求出半圆形的面积。
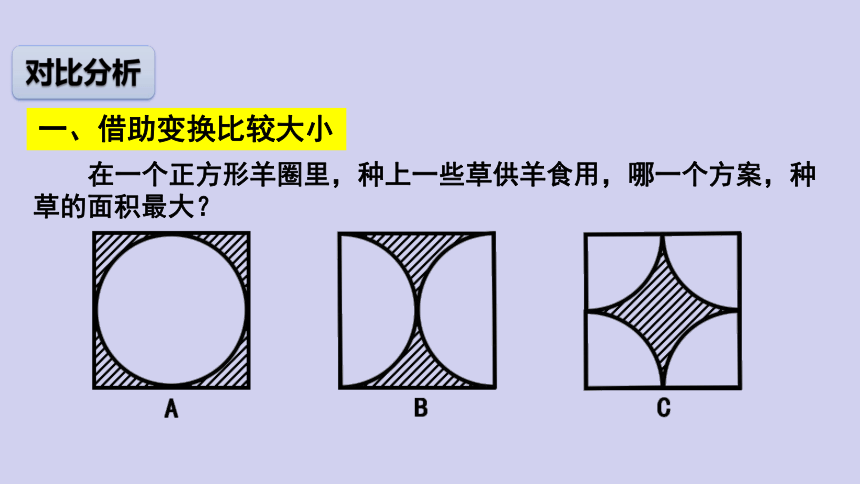
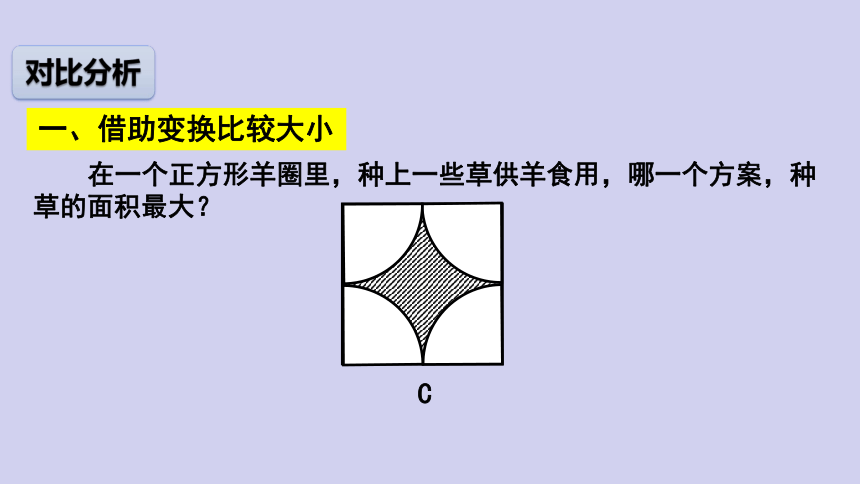
在一个正方形羊圈里,种上一些草供羊食用,哪一个方案,种草的面积最大?
一、借助变换比较大小
对比分析
一、借助变换比较大小
对比分析
S=S正-S圆
A
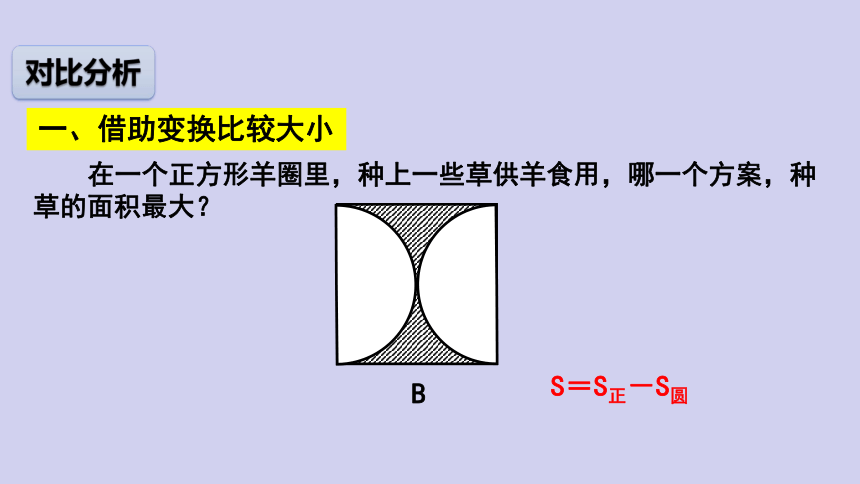
在一个正方形羊圈里,种上一些草供羊食用,哪一个方案,种草的面积最大?
一、借助变换比较大小
对比分析
B
S=S正-S圆
在一个正方形羊圈里,种上一些草供羊食用,哪一个方案,种草的面积最大?
一、借助变换比较大小
对比分析
C
在一个正方形羊圈里,种上一些草供羊食用,哪一个方案,种草的面积最大?
一、借助变换比较大小
对比分析
C
S=S正-S圆
在一个正方形羊圈里,种上一些草供羊食用,哪一个方案,种草的面积最大?
通过图形的平移或旋转,可以把不规则图形转化为规则图形。
用同样大小的正方形铁皮,分别按下面两种方式剪出不同规格的圆片,剪完圆片后,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
用同样大小的正方形铁皮,分别按下面两种方式剪出不同规格的圆片,剪完圆片后,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
假设正方形铁皮的边长是6cm,由此可知方式A中,一个圆的直径是6cm。
则方式A中,剩下边角料的面积是:
6×6-π×(6÷2) =36-9π=7.74(cm )
赋值法
6cm
6cm
用同样大小的正方形铁皮,分别按下面两种方式剪出不同规格的圆片,剪完圆片后,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
假设正方形铁皮的边长是6cm,由此可知方式B中,一个圆的直径是3cm。
则方式B中,剩下边角料的面积是:
6×6-π×(3÷2) ×4=36-9π=7.74(cm )
赋值法
6cm
3cm
用同样大小的正方形铁皮,分别按下面两种方式剪出不同规格的圆片,剪完圆片后,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
a
a
假设正方形铁皮的边长是a,由此可知方式A中,一个圆的直径是a。
则方式A中,剩下边角料的面积是:
a×a-π×(a÷2) =a - πa =(1- π)a
代数法
假设正方形铁皮的边长是a,由此可知方式B中,一个圆的直径是0.5a。
则方式B中,剩下边角料的面积是:
a×a-π×(0.5a÷2) ×4=a - πa ×4=(1- π)a
16
1
4
1
用同样大小的正方形铁皮,分别按下面两种方式剪出不同规格的圆片,剪完圆片后,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
代数法
a
0.5a
除了观察比较,还可以应用赋值法和代数法去分析与解决问题。
假设正方形铁皮的边长是6cm,由此可知方式C中,一个圆的直径是2cm。
则方式C中,剩下边角料的面积是:
6×6-π×(2÷2) ×9=36-9π=7.74(cm )
用同样大小的正方形铁皮,按下面的方式剪出圆片,剪完圆片后,与前面的剪法相比,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
赋值法
6cm
2cm
假设正方形铁皮的边长是a,由此可知方式C中,一个圆的直径是 a。
则方式C中,剩下边角料的面积是:
a×a-π×( a÷2) ×9=a - πa ×9=(1- π)a
36
1
3
1
3
1
4
1
二、应用赋值法和代数法解题
对比分析
代数法
a
用同样大小的正方形铁皮,按下面的方式剪出圆片,剪完圆片后,与前面的剪法相比,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
用同样大小的正方形铁皮,按下面的方式剪出圆片,剪完圆片后,与前面的剪法相比,哪张铁皮剩下的边角料更多?
对比分析
用同样大小的正方形铁皮,按等列等行的排列方式,剪下尽可能多的完全相同的圆片后,剩下边角料的面积都相等。
1 1 1 1 1
1
S
1
S
(1 -S)
S
4
S
(1 -S)
S
9
S
(1 -S)
S
16
S
(1 -S)
S
25
S
(1 -S)
……
……
……
……
……
……
1
1
n
S
(1 -S)
假设图中圆的半径是1cm,则大正方形的边长是2cm。
由此可知,
大正方形的面积是:2×2=4(cm )
圆的面积是:π×1 =π(cm )
小正方形的面积是:1×1÷2×4=2(cm )
因而,这时大正方形与小正方形的面积比是4:2=2:1。
三、赋值法与代数法的对比
对比分析
A.π:4 B.1:2 C.2:1 D.4:π
赋值法
2cm
1cm
1cm
C
如图,在一个正方形中画一个最大的圆形,再在圆形中画一个最大的正方形,这时,大正方形与小正方形的面积比是( )。
假设图中圆的半径是2cm,则大正方形的边长是4cm。
由此可知,
大正方形的面积是:4×4=16(cm )
圆的面积是:π×2 =4π(cm )
小正方形的面积是:2×2÷2×4=8(cm )
因而,这时大正方形与小正方形的面积比是16:8=2:1。
三、赋值法与代数法的对比
对比分析
A.π:4 B.1:2 C.2:1 D.4:π
赋值法
4cm
2cm
2cm
C
如图,在一个正方形中画一个最大的圆形,再在圆形中画一个最大的正方形,这时,大正方形与小正方形的面积比是( )。
假设图中圆的半径是3cm,则大正方形的边长是6cm。
由此可知,
大正方形的面积是:6×6=36(cm )
圆的面积是:π×3 =9π(cm )
小正方形的面积是:3×3÷2×4=18(cm )
因而,这时大正方形与小正方形的面积比是36:18=2:1。
三、赋值法与代数法的对比
对比分析
A.π:4 B.1:2 C.2:1 D.4:π
赋值法
6cm
3cm
3cm
C
如图,在一个正方形中画一个最大的圆形,再在圆形中画一个最大的正方形,这时,大正方形与小正方形的面积比是( )。
假设图中圆的半径是r,则大正方形的边长是2r。
由此可知,
大正方形的面积是:2r×2r=4r
圆的面积是:π×r =πr
小正方形的面积是:r×r÷2×4=2r
因而,这时大正方形与小正方形的面积比是4r :2r =2:1。
三、赋值法与代数法的对比
对比分析
A.π:4 B.1:2 C.2:1 D.4:π
代数法
2r
r
r
C
如图,在一个正方形中画一个最大的圆形,再在圆形中画一个最大的正方形,这时,大正方形与小正方形的面积比是( )。
三、赋值法与代数法的对比
对比分析
A.π:4 B.1:2 C.2:1 D.4:π
从赋值法到代数法
2r
r
r
C
与赋值法相比,代数法更严谨、更有说服力。
如图,在一个正方形中画一个最大的圆形,再在圆形中画一个最大的正方形,这时,大正方形与小正方形的面积比是( )。
圆的面积综合练习课
r
全课小结
d
C
S=πr
r=d÷2
r=C÷π÷2
未知
已知
赋值法、代数法
课后练习
1.选择。
要在公园的同一块地里,设计不同形状的花圃,三个方案设计的花圃面积相比较,( )。
2.选择。
如图,把圆转化为一个近似长方形后,近似长方形与圆相比较,( )。
A. 面积不变,周长变
B. 周长不变,面积变
C. 周长和面积都不变
D. 周长和面积都变
3.选择。
如图,若图中有3个同心圆,圆心都是O,并且OA=AB=1.5BC,则圆环甲的面积与圆环乙的面积相比较,( )。
A.甲的面积大 B.乙的面积大 C.甲、乙的面积一样大 D.无法判断
六年级—人教版—数学—第五单元
圆的面积综合练习课(答疑)
这是一个关于阿凡提的故事。有一户人家的羊群日渐长大,原来的长方形羊圈逐渐显得拥挤,可是仓库里已经没有更多的木栅栏去建造新的羊圈了。不过,聪明的阿凡提只是把羊圈改了个形状,就使得羊圈的面积比原来更大了。同学们,你们知道阿凡提把羊圈改成了什么形状吗?
用同样长的木栅栏,怎样围才能使得羊圈的面积最大?
课堂答疑
选择:
用一根铁丝分别围成一个长方形、正方形、圆形,( )的面积最大。
A.长方形 B.正方形 C.圆形 D.不能确定
选择:
用一根铁丝分别围成一个长方形、正方形、圆形,( )的面积最大。
A.长方形 B.正方形 C.圆形 D.不能确定
课堂答疑
C
已知周长相等时,正方形面积>长方形面积,
故可假设这根铁丝长为4π。则
正方形边长为 ,面积为:π×π
圆的半径为 ,面积为:π×2×2=4π
显然,4π>π×π,即圆面积大于正方形面积,因此选C。
4
4π
=
π
4π
=
2
2π
赋值法
选择:
用一根铁丝分别围成一个长方形、正方形、圆形,( )的面积最大。
A.长方形 B.正方形 C.圆形 D.不能确定
课堂答疑
C
代数法
周长相等的平面图形中,圆的面积最大。
同学们,你们现在知道阿凡提把羊圈改成什么形状了吗?
用同样长的木栅栏围成圆形的羊圈,面积最大。
谢谢观看!
六年级—人教版—数学—第五单元
圆的面积综合练习课
1.理解与掌握圆的面积计算公式,并据此解决一些简单的实际问题。
2.体验与理解通过赋值法和代数法解决实际问题的解题思路。
3.沟通知识点间的内在联系,进一步体会和理解转化的数学思想与方法。
学习目标
圆的面积指的是什么?用什么单位来计量?
圆的面积是指圆所占平面的大小。
用面积单位来计量圆的面积,如cm 、dm 、m 等。
一、圆的面积的意义
知识回顾
S=πr
怎样求圆的面积?
如图,计算下面图形中的阴影部分面积。
(1)S=πr
=π×6
=36π
=113.04(dm )
二、计算阴影部分的面积
知识回顾
(2)113.04× =84.78(dm )
4
3
依照公式,根据半径可计算出圆的面积。
1.如图,如果正方形的面积是100cm ,那么圆的面积是多少cm ?
三、灵活求圆的面积
知识回顾
由r×r=100,可知r =100,
根据S=πr ,可知
圆的面积是:S=πr =π×100=100π=314(cm )
由r×r=100,可知r=10,
根据S=πr ,可知
圆的面积是:S=πr =π×10 =100π=314(cm )
解法一
解法二
2.如图,如果正方形的面积是10cm ,那么圆的面积是多少cm ?
三、灵活求圆的面积
知识回顾
由r×r=10,可知r =10,
根据S=πr ,可知
圆的面积是:S=πr =π×10=10π=31.4(cm )
3.如图,如果三角形的面积是15cm ,那么圆的面积是多少cm ?
三、灵活求圆的面积
知识回顾
由r×r÷2=15,可知r =30,
根据S=πr ,可知
圆的面积是:S=πr =π×30=30π=94.2(cm )
根据公式,可推算出圆的面积。
如图,若半圆形的周长是30.84cm,则半圆形的面积是多少cm ?
四、求半圆形的面积
知识回顾
(1)解:设这个圆的半径是rcm。
πr+2r=30.84
(π+2 )r=30.84
5.14r=30.84
r=30.84÷5.14
r=6
(2)S半=πr ÷2
=π×6 ÷2
=36π÷2
=18π
=56.52(cm )
逆向运用公式求出圆的半径后,再求出半圆形的面积。
在一个正方形羊圈里,种上一些草供羊食用,哪一个方案,种草的面积最大?
一、借助变换比较大小
对比分析
一、借助变换比较大小
对比分析
S=S正-S圆
A
在一个正方形羊圈里,种上一些草供羊食用,哪一个方案,种草的面积最大?
一、借助变换比较大小
对比分析
B
S=S正-S圆
在一个正方形羊圈里,种上一些草供羊食用,哪一个方案,种草的面积最大?
一、借助变换比较大小
对比分析
C
在一个正方形羊圈里,种上一些草供羊食用,哪一个方案,种草的面积最大?
一、借助变换比较大小
对比分析
C
S=S正-S圆
在一个正方形羊圈里,种上一些草供羊食用,哪一个方案,种草的面积最大?
通过图形的平移或旋转,可以把不规则图形转化为规则图形。
用同样大小的正方形铁皮,分别按下面两种方式剪出不同规格的圆片,剪完圆片后,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
用同样大小的正方形铁皮,分别按下面两种方式剪出不同规格的圆片,剪完圆片后,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
假设正方形铁皮的边长是6cm,由此可知方式A中,一个圆的直径是6cm。
则方式A中,剩下边角料的面积是:
6×6-π×(6÷2) =36-9π=7.74(cm )
赋值法
6cm
6cm
用同样大小的正方形铁皮,分别按下面两种方式剪出不同规格的圆片,剪完圆片后,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
假设正方形铁皮的边长是6cm,由此可知方式B中,一个圆的直径是3cm。
则方式B中,剩下边角料的面积是:
6×6-π×(3÷2) ×4=36-9π=7.74(cm )
赋值法
6cm
3cm
用同样大小的正方形铁皮,分别按下面两种方式剪出不同规格的圆片,剪完圆片后,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
a
a
假设正方形铁皮的边长是a,由此可知方式A中,一个圆的直径是a。
则方式A中,剩下边角料的面积是:
a×a-π×(a÷2) =a - πa =(1- π)a
代数法
假设正方形铁皮的边长是a,由此可知方式B中,一个圆的直径是0.5a。
则方式B中,剩下边角料的面积是:
a×a-π×(0.5a÷2) ×4=a - πa ×4=(1- π)a
16
1
4
1
用同样大小的正方形铁皮,分别按下面两种方式剪出不同规格的圆片,剪完圆片后,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
代数法
a
0.5a
除了观察比较,还可以应用赋值法和代数法去分析与解决问题。
假设正方形铁皮的边长是6cm,由此可知方式C中,一个圆的直径是2cm。
则方式C中,剩下边角料的面积是:
6×6-π×(2÷2) ×9=36-9π=7.74(cm )
用同样大小的正方形铁皮,按下面的方式剪出圆片,剪完圆片后,与前面的剪法相比,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
赋值法
6cm
2cm
假设正方形铁皮的边长是a,由此可知方式C中,一个圆的直径是 a。
则方式C中,剩下边角料的面积是:
a×a-π×( a÷2) ×9=a - πa ×9=(1- π)a
36
1
3
1
3
1
4
1
二、应用赋值法和代数法解题
对比分析
代数法
a
用同样大小的正方形铁皮,按下面的方式剪出圆片,剪完圆片后,与前面的剪法相比,哪张铁皮剩下的边角料更多?
二、应用赋值法和代数法解题
对比分析
用同样大小的正方形铁皮,按下面的方式剪出圆片,剪完圆片后,与前面的剪法相比,哪张铁皮剩下的边角料更多?
对比分析
用同样大小的正方形铁皮,按等列等行的排列方式,剪下尽可能多的完全相同的圆片后,剩下边角料的面积都相等。
1 1 1 1 1
1
S
1
S
(1 -S)
S
4
S
(1 -S)
S
9
S
(1 -S)
S
16
S
(1 -S)
S
25
S
(1 -S)
……
……
……
……
……
……
1
1
n
S
(1 -S)
假设图中圆的半径是1cm,则大正方形的边长是2cm。
由此可知,
大正方形的面积是:2×2=4(cm )
圆的面积是:π×1 =π(cm )
小正方形的面积是:1×1÷2×4=2(cm )
因而,这时大正方形与小正方形的面积比是4:2=2:1。
三、赋值法与代数法的对比
对比分析
A.π:4 B.1:2 C.2:1 D.4:π
赋值法
2cm
1cm
1cm
C
如图,在一个正方形中画一个最大的圆形,再在圆形中画一个最大的正方形,这时,大正方形与小正方形的面积比是( )。
假设图中圆的半径是2cm,则大正方形的边长是4cm。
由此可知,
大正方形的面积是:4×4=16(cm )
圆的面积是:π×2 =4π(cm )
小正方形的面积是:2×2÷2×4=8(cm )
因而,这时大正方形与小正方形的面积比是16:8=2:1。
三、赋值法与代数法的对比
对比分析
A.π:4 B.1:2 C.2:1 D.4:π
赋值法
4cm
2cm
2cm
C
如图,在一个正方形中画一个最大的圆形,再在圆形中画一个最大的正方形,这时,大正方形与小正方形的面积比是( )。
假设图中圆的半径是3cm,则大正方形的边长是6cm。
由此可知,
大正方形的面积是:6×6=36(cm )
圆的面积是:π×3 =9π(cm )
小正方形的面积是:3×3÷2×4=18(cm )
因而,这时大正方形与小正方形的面积比是36:18=2:1。
三、赋值法与代数法的对比
对比分析
A.π:4 B.1:2 C.2:1 D.4:π
赋值法
6cm
3cm
3cm
C
如图,在一个正方形中画一个最大的圆形,再在圆形中画一个最大的正方形,这时,大正方形与小正方形的面积比是( )。
假设图中圆的半径是r,则大正方形的边长是2r。
由此可知,
大正方形的面积是:2r×2r=4r
圆的面积是:π×r =πr
小正方形的面积是:r×r÷2×4=2r
因而,这时大正方形与小正方形的面积比是4r :2r =2:1。
三、赋值法与代数法的对比
对比分析
A.π:4 B.1:2 C.2:1 D.4:π
代数法
2r
r
r
C
如图,在一个正方形中画一个最大的圆形,再在圆形中画一个最大的正方形,这时,大正方形与小正方形的面积比是( )。
三、赋值法与代数法的对比
对比分析
A.π:4 B.1:2 C.2:1 D.4:π
从赋值法到代数法
2r
r
r
C
与赋值法相比,代数法更严谨、更有说服力。
如图,在一个正方形中画一个最大的圆形,再在圆形中画一个最大的正方形,这时,大正方形与小正方形的面积比是( )。
圆的面积综合练习课
r
全课小结
d
C
S=πr
r=d÷2
r=C÷π÷2
未知
已知
赋值法、代数法
课后练习
1.选择。
要在公园的同一块地里,设计不同形状的花圃,三个方案设计的花圃面积相比较,( )。
2.选择。
如图,把圆转化为一个近似长方形后,近似长方形与圆相比较,( )。
A. 面积不变,周长变
B. 周长不变,面积变
C. 周长和面积都不变
D. 周长和面积都变
3.选择。
如图,若图中有3个同心圆,圆心都是O,并且OA=AB=1.5BC,则圆环甲的面积与圆环乙的面积相比较,( )。
A.甲的面积大 B.乙的面积大 C.甲、乙的面积一样大 D.无法判断
六年级—人教版—数学—第五单元
圆的面积综合练习课(答疑)
这是一个关于阿凡提的故事。有一户人家的羊群日渐长大,原来的长方形羊圈逐渐显得拥挤,可是仓库里已经没有更多的木栅栏去建造新的羊圈了。不过,聪明的阿凡提只是把羊圈改了个形状,就使得羊圈的面积比原来更大了。同学们,你们知道阿凡提把羊圈改成了什么形状吗?
用同样长的木栅栏,怎样围才能使得羊圈的面积最大?
课堂答疑
选择:
用一根铁丝分别围成一个长方形、正方形、圆形,( )的面积最大。
A.长方形 B.正方形 C.圆形 D.不能确定
选择:
用一根铁丝分别围成一个长方形、正方形、圆形,( )的面积最大。
A.长方形 B.正方形 C.圆形 D.不能确定
课堂答疑
C
已知周长相等时,正方形面积>长方形面积,
故可假设这根铁丝长为4π。则
正方形边长为 ,面积为:π×π
圆的半径为 ,面积为:π×2×2=4π
显然,4π>π×π,即圆面积大于正方形面积,因此选C。
4
4π
=
π
4π
=
2
2π
赋值法
选择:
用一根铁丝分别围成一个长方形、正方形、圆形,( )的面积最大。
A.长方形 B.正方形 C.圆形 D.不能确定
课堂答疑
C
代数法
周长相等的平面图形中,圆的面积最大。
同学们,你们现在知道阿凡提把羊圈改成什么形状了吗?
用同样长的木栅栏围成圆形的羊圈,面积最大。
谢谢观看!
