鲁教版(五四制)数学七年级下册 第十章 三角形的有关证明 复习 课件(共45张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级下册 第十章 三角形的有关证明 复习 课件(共45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1021.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 19:09:32 | ||
图片预览










文档简介
(共45张PPT)
第十章 三角形的有关证明
复习课件
┃知识归纳┃
1.等腰三角形的性质
性质(1):等腰三角形的两个底角______。
性质(2):等腰三角形顶角的_______、底边上的______、底边上的高互相重合。
2.等腰三角形的判定
(1)定义:有两条边______的三角形是等腰三角形。
(2)等角对等边:有两个角______的三角形是等腰三角形。
相等
平分线
中线
相等
相等
3.用反证法证明的一般步骤
(1)假设命题的结论不成立;
(2)从这个假设出发,应用正确的推论方法,得出与定义、公理、已证定理或已知条件相矛盾的结果;
(3)由矛盾的结果判定假设不正确,从而肯定命题的结论正确。
4.等边三角形的判定
(1)有一个角等于60°的_____三角形是等边三角形;
等腰
(2)三边相等的三角形叫做等边三角形;
(3)三个角相等的三角形是等边三角形;
(4)有两个角等于60°的三角形是等边三角形。
5.直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的______。
6.勾股定理及其逆定理
勾股定理:直角三角形两条直角边的平方和等于斜边的_____。
一半
平方
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是______三角形。
7.线段的垂直平分线的性质定理及判定定理
性质定理:线段的垂直平分线上的点到这条线段两个端点的距离_____。
判定定理:到一条线段两个端点距离相等的点,在这条线段的____________上。
【点拨】线段的垂直平分线可以看作和线段两个端点距离相等的所有点的集合。
直角
相等
垂直平分线
8.三线共点
三角形三条边的垂直平分线相交于______,并且这一点到三角形三个顶点的距离_____。
9.角平分线的性质定理及判定定理
性质定理:角平分线上的点到这个角两边的距离_____。
判定定理:在一个角的内部,且到角的两边______相等的点,在这个角的平分线上。
相等
相等
距离
一点
【注意】角的平分线是在角的内部的一条射线,所以它的逆定理必须加上“在角的内部”这个条件。
10.三角形三条角平分线的性质
三角形的三条角平分线相交于一点,并且这一点到三条边的距离_____。
相等
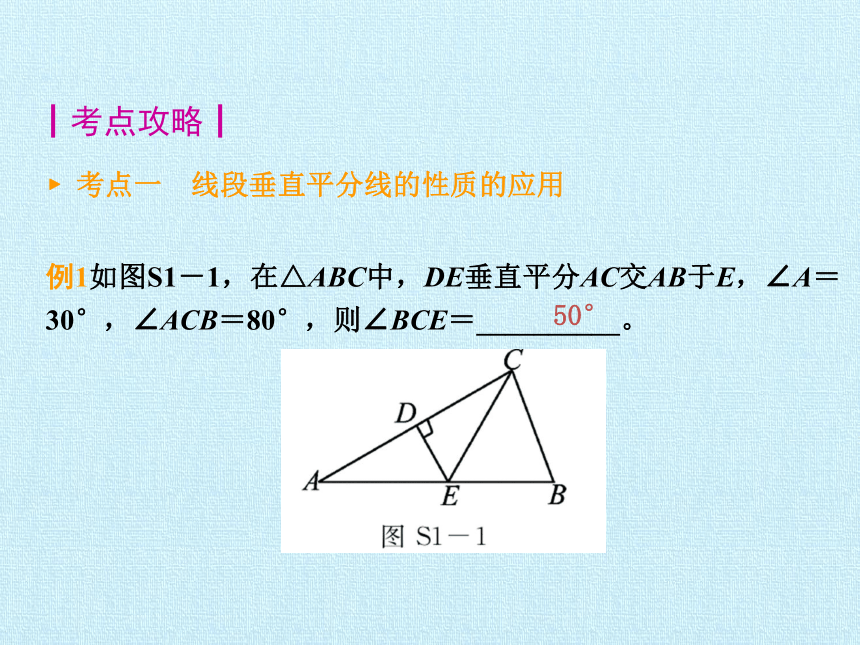
考点一 线段垂直平分线的性质的应用
┃考点攻略┃
例1如图S1-1,在△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE=__________。
50°
【解析】根据线段垂直平分线的性质,线段垂直平分线上的点到线段两端点的距离相等,所以EA=EC,∠A=∠ACE=30°,又∠ACB=80°,故∠BCE=80°—30°=50°。
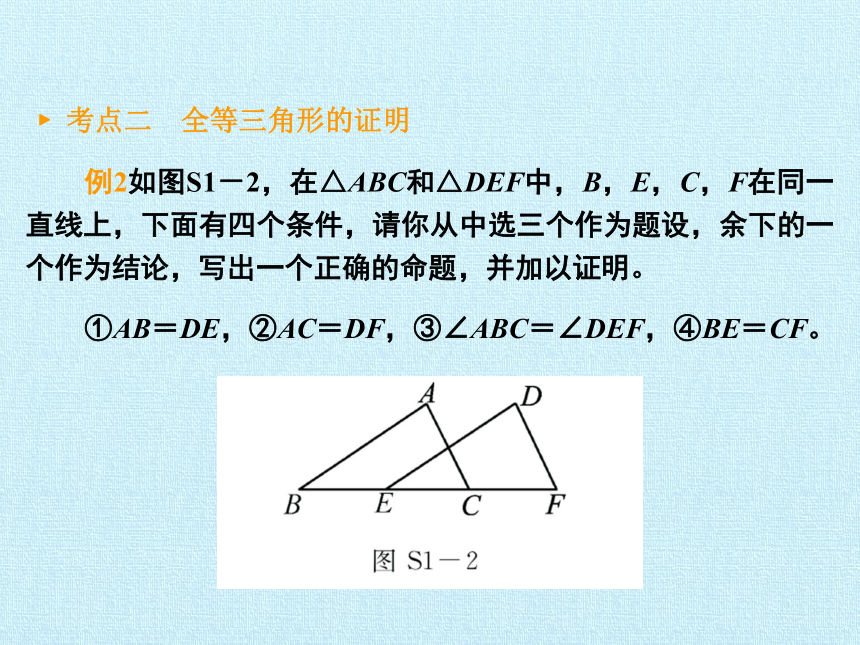
考点二 全等三角形的证明
例2如图S1-2,在△ABC和△DEF中,B,E,C,F在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明。
①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF。
解:答案不惟一,命题一:在△ABC和△DEF中,B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF。求证:∠ABC=∠DEF。
命题二:在△ABC和△DEF中,B,E,C,F在同一直线上,AB=DE,∠ABC=∠DEF,BE=CF。求证:AC=DF。
下面证明命题一:
已知:如题图,在△ABC和△DEF中,B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF。
求证:∠ABC=∠DEF。
证明:在△ABC和△DEF中,
∵BE=CF,∴BC=EF。
又∵AB=DE,AC=DF,
∴△ABC≌△DEF(SSS)。
∴∠ABC=∠DEF。
考点三 勾股定理的应用
【解析】这个有趣的问题是勾股定理的典型应用,此问题看上去是一个曲面上的路线问题,但实际上能通过圆柱的侧面展开而转化为平面上的路线问题,值得注意的是,在剪开圆柱侧面时,要从A开始并垂直于AB剪开,这样展开的侧面才是个矩形,才能得到直角,再利用勾股定理解决此问题。
解:将圆柱的侧面展开,如图S1-4,圆柱的底面周长为2πr=2×π×=4,取其一半:×4=2,圆柱的高为2,根据勾股定理,得AC2=22+22=8,所以AC=2。
考点四 等腰三角形的判别
例4 已知:在△ABC中,∠A=90°,AB=AC,D为BC的中点。
(1)如图S1-5,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论。
【解析】要证明△DEF为等腰三角形,需要证DE=DF。连接AD,利用全等可得这一结论。至于在延长线上,可利用同样的方法。
图S1-5
解:(1)证明:连接AD,如图S1-6:
∵AB=AC,∠BAC=90°,D为BC的中点,
∴AD⊥BC,BD=AD,
∴∠B=∠DAC=45°,
又BE=AF,
∴△BDE≌△ADF(SAS),
∴ED=FD,∠BDE=∠ADF,
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,
∴△DEF为等腰直角三角形。
(2)若E,F分别是AB,CA延长线上的点,如图S1-7所示:
连接AD,
∵AB=AC,∠BAC=90°,D为BC的中点,
∴AD=BD,AD⊥BC,
∴∠DAC=∠ABD=45°,
∴∠DAF=∠DBE=135°。
又AF=BE,
∴△DAF≌△DBE(SAS),
图S1-7
∴FD=ED,∠FDA=∠EDB,
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°,
∴△DEF仍为等腰直角三角形。
考点五 角平分线与“截长补短”
例5 如图S1-8,AD∥BC,点E在线段AB上,∠ADE=∠CDE,∠DCE=∠ECB。
求证:CD=AD+BC。
图S1-8
【解析】结论是CD=AD+BC,可考虑用“截长补短法”中的“截长”,即在CD上截取CF=CB,只要再证DF=DA即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的。
图S1-9
证明:在CD上截取CF=BC,如图S1-9,
在△FCE与△BCE中,
∴△FCE≌△BCE(SAS),
∴∠2=∠1。
∵AD∥BC,∴∠ADC+∠BCD=180°。
又∠ADE=∠CDE,
∴∠DCE+∠CDE=90°,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4。
在△FDE与△ADE中,
∴△FDE≌△ADE(ASA),∴DF=DA。
∵CD=DF+CF,∴CD=AD+BC。
1.以下命题中,是真命题的是( )
A.两条直线只有相交和平行两种位置关系
B.同位角相等
C.两边和一角对应相等的两个三角形全等
D.等腰三角形底边中点到两腰的距离相等
D
2.下列说法中,正确的是( )
A.等腰三角形边上的中线也是高
B.等腰三角形的内角平分线的交点到三个顶点的距离相等
C.等边三角形每条角平分线都平分对边
D.直角三角形一边上的中线等于这边的一半
C
3.在直角三角形中,一条直角边长为a,另一条边长为2a,那么它的三个内角之比为( )
A.1∶2∶3
B.2∶2∶1
C.1∶1∶2
D.以上都不对
D
4.如图S1-9,△ABC中,∠ACB=90°,BA的垂直平分线交CB边于D,若AB=10,AC=5,则图中等于60°的角的个数为( )
A.2
B.3
C.4
D.5
D
图S1-10
5.如图S1-11,在Rt△ABC中,∠C=90°,∠B=15°,DE是AB的中垂线,垂足为D,交BC于点E,若BE=4,则AC=________。
2
图S1-11
6.若点P是△ABC内一点,PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,且PD=PE=PF,则点P是△ABC的( )
A.三条高的交点
B.三条中线的交点
C.三条角平分线的交点
D.三条中垂线的交点
C
7.在平面内,到A,B,C三点距离相等的点有( )
A.只有一个
B.有两个
C.有三个或三个以上
D.有一个或没有
D
8.小明家有一块△ABC的土地,如图S1-12所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5∶7∶9的三部分,分别种植不同的农作物,请你设计一种方案。
图S1-12
解:如图S1-13所示,分别作∠ACB和∠ABC的平分线,相交于点D,连接AD,则S△ADC∶S△ADB∶S△BDC=5∶7∶9。
图S1-13
9.如图S1-14,在四边形ABCD中,AD∥BC,E为CD的中点,连结AE,BE,BE⊥AE,延长AE交BC的延长线于点F。
求证:(1)FC=AD;
(2)AB=BC+AD。
证明:(1)因为E是CD的中点,所以DE=CE。
因为AD∥BC,所以∠ADE=∠FCE,∠DAE=∠CFE。所以△ADE≌△FCE。所以FC=AD。
(2)因为△ADE≌△FCE,所以AE=FE。又因为BE⊥AE,所以BE是线段AF的垂直平分线,所以AB=FB。因为FB=BC+FC=BC+AD。所以AB=BC+AD。
10.如图S1-15①,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM,CN交于F点。
(1)求证:AN=BM;
(2)求证:△CEF为等边三角形;
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在图②中补出符合要求的图形,并判断第(1)(2)两小题的结论是否仍然成立。(不要求证明)
解:(1)证明:易证△CMB≌△CAN,则AN=BM。
(2)证明:∵△CMB≌△CAN,∴∠ANC=∠MBC。又∵∠MCN=∠FCB=60°,
BC=CN,
∴△ECN≌△FCB,∴CE=CF。
又∵∠ECF=60°,∴△ECF是等边三角形。
(3)如图②所示,(1)小题的结论仍然成立,(2)小题不成立。
谢 谢
第十章 三角形的有关证明
复习课件
┃知识归纳┃
1.等腰三角形的性质
性质(1):等腰三角形的两个底角______。
性质(2):等腰三角形顶角的_______、底边上的______、底边上的高互相重合。
2.等腰三角形的判定
(1)定义:有两条边______的三角形是等腰三角形。
(2)等角对等边:有两个角______的三角形是等腰三角形。
相等
平分线
中线
相等
相等
3.用反证法证明的一般步骤
(1)假设命题的结论不成立;
(2)从这个假设出发,应用正确的推论方法,得出与定义、公理、已证定理或已知条件相矛盾的结果;
(3)由矛盾的结果判定假设不正确,从而肯定命题的结论正确。
4.等边三角形的判定
(1)有一个角等于60°的_____三角形是等边三角形;
等腰
(2)三边相等的三角形叫做等边三角形;
(3)三个角相等的三角形是等边三角形;
(4)有两个角等于60°的三角形是等边三角形。
5.直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的______。
6.勾股定理及其逆定理
勾股定理:直角三角形两条直角边的平方和等于斜边的_____。
一半
平方
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是______三角形。
7.线段的垂直平分线的性质定理及判定定理
性质定理:线段的垂直平分线上的点到这条线段两个端点的距离_____。
判定定理:到一条线段两个端点距离相等的点,在这条线段的____________上。
【点拨】线段的垂直平分线可以看作和线段两个端点距离相等的所有点的集合。
直角
相等
垂直平分线
8.三线共点
三角形三条边的垂直平分线相交于______,并且这一点到三角形三个顶点的距离_____。
9.角平分线的性质定理及判定定理
性质定理:角平分线上的点到这个角两边的距离_____。
判定定理:在一个角的内部,且到角的两边______相等的点,在这个角的平分线上。
相等
相等
距离
一点
【注意】角的平分线是在角的内部的一条射线,所以它的逆定理必须加上“在角的内部”这个条件。
10.三角形三条角平分线的性质
三角形的三条角平分线相交于一点,并且这一点到三条边的距离_____。
相等
考点一 线段垂直平分线的性质的应用
┃考点攻略┃
例1如图S1-1,在△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE=__________。
50°
【解析】根据线段垂直平分线的性质,线段垂直平分线上的点到线段两端点的距离相等,所以EA=EC,∠A=∠ACE=30°,又∠ACB=80°,故∠BCE=80°—30°=50°。
考点二 全等三角形的证明
例2如图S1-2,在△ABC和△DEF中,B,E,C,F在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明。
①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF。
解:答案不惟一,命题一:在△ABC和△DEF中,B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF。求证:∠ABC=∠DEF。
命题二:在△ABC和△DEF中,B,E,C,F在同一直线上,AB=DE,∠ABC=∠DEF,BE=CF。求证:AC=DF。
下面证明命题一:
已知:如题图,在△ABC和△DEF中,B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF。
求证:∠ABC=∠DEF。
证明:在△ABC和△DEF中,
∵BE=CF,∴BC=EF。
又∵AB=DE,AC=DF,
∴△ABC≌△DEF(SSS)。
∴∠ABC=∠DEF。
考点三 勾股定理的应用
【解析】这个有趣的问题是勾股定理的典型应用,此问题看上去是一个曲面上的路线问题,但实际上能通过圆柱的侧面展开而转化为平面上的路线问题,值得注意的是,在剪开圆柱侧面时,要从A开始并垂直于AB剪开,这样展开的侧面才是个矩形,才能得到直角,再利用勾股定理解决此问题。
解:将圆柱的侧面展开,如图S1-4,圆柱的底面周长为2πr=2×π×=4,取其一半:×4=2,圆柱的高为2,根据勾股定理,得AC2=22+22=8,所以AC=2。
考点四 等腰三角形的判别
例4 已知:在△ABC中,∠A=90°,AB=AC,D为BC的中点。
(1)如图S1-5,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论。
【解析】要证明△DEF为等腰三角形,需要证DE=DF。连接AD,利用全等可得这一结论。至于在延长线上,可利用同样的方法。
图S1-5
解:(1)证明:连接AD,如图S1-6:
∵AB=AC,∠BAC=90°,D为BC的中点,
∴AD⊥BC,BD=AD,
∴∠B=∠DAC=45°,
又BE=AF,
∴△BDE≌△ADF(SAS),
∴ED=FD,∠BDE=∠ADF,
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,
∴△DEF为等腰直角三角形。
(2)若E,F分别是AB,CA延长线上的点,如图S1-7所示:
连接AD,
∵AB=AC,∠BAC=90°,D为BC的中点,
∴AD=BD,AD⊥BC,
∴∠DAC=∠ABD=45°,
∴∠DAF=∠DBE=135°。
又AF=BE,
∴△DAF≌△DBE(SAS),
图S1-7
∴FD=ED,∠FDA=∠EDB,
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°,
∴△DEF仍为等腰直角三角形。
考点五 角平分线与“截长补短”
例5 如图S1-8,AD∥BC,点E在线段AB上,∠ADE=∠CDE,∠DCE=∠ECB。
求证:CD=AD+BC。
图S1-8
【解析】结论是CD=AD+BC,可考虑用“截长补短法”中的“截长”,即在CD上截取CF=CB,只要再证DF=DA即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的。
图S1-9
证明:在CD上截取CF=BC,如图S1-9,
在△FCE与△BCE中,
∴△FCE≌△BCE(SAS),
∴∠2=∠1。
∵AD∥BC,∴∠ADC+∠BCD=180°。
又∠ADE=∠CDE,
∴∠DCE+∠CDE=90°,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4。
在△FDE与△ADE中,
∴△FDE≌△ADE(ASA),∴DF=DA。
∵CD=DF+CF,∴CD=AD+BC。
1.以下命题中,是真命题的是( )
A.两条直线只有相交和平行两种位置关系
B.同位角相等
C.两边和一角对应相等的两个三角形全等
D.等腰三角形底边中点到两腰的距离相等
D
2.下列说法中,正确的是( )
A.等腰三角形边上的中线也是高
B.等腰三角形的内角平分线的交点到三个顶点的距离相等
C.等边三角形每条角平分线都平分对边
D.直角三角形一边上的中线等于这边的一半
C
3.在直角三角形中,一条直角边长为a,另一条边长为2a,那么它的三个内角之比为( )
A.1∶2∶3
B.2∶2∶1
C.1∶1∶2
D.以上都不对
D
4.如图S1-9,△ABC中,∠ACB=90°,BA的垂直平分线交CB边于D,若AB=10,AC=5,则图中等于60°的角的个数为( )
A.2
B.3
C.4
D.5
D
图S1-10
5.如图S1-11,在Rt△ABC中,∠C=90°,∠B=15°,DE是AB的中垂线,垂足为D,交BC于点E,若BE=4,则AC=________。
2
图S1-11
6.若点P是△ABC内一点,PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,且PD=PE=PF,则点P是△ABC的( )
A.三条高的交点
B.三条中线的交点
C.三条角平分线的交点
D.三条中垂线的交点
C
7.在平面内,到A,B,C三点距离相等的点有( )
A.只有一个
B.有两个
C.有三个或三个以上
D.有一个或没有
D
8.小明家有一块△ABC的土地,如图S1-12所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5∶7∶9的三部分,分别种植不同的农作物,请你设计一种方案。
图S1-12
解:如图S1-13所示,分别作∠ACB和∠ABC的平分线,相交于点D,连接AD,则S△ADC∶S△ADB∶S△BDC=5∶7∶9。
图S1-13
9.如图S1-14,在四边形ABCD中,AD∥BC,E为CD的中点,连结AE,BE,BE⊥AE,延长AE交BC的延长线于点F。
求证:(1)FC=AD;
(2)AB=BC+AD。
证明:(1)因为E是CD的中点,所以DE=CE。
因为AD∥BC,所以∠ADE=∠FCE,∠DAE=∠CFE。所以△ADE≌△FCE。所以FC=AD。
(2)因为△ADE≌△FCE,所以AE=FE。又因为BE⊥AE,所以BE是线段AF的垂直平分线,所以AB=FB。因为FB=BC+FC=BC+AD。所以AB=BC+AD。
10.如图S1-15①,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM,CN交于F点。
(1)求证:AN=BM;
(2)求证:△CEF为等边三角形;
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在图②中补出符合要求的图形,并判断第(1)(2)两小题的结论是否仍然成立。(不要求证明)
解:(1)证明:易证△CMB≌△CAN,则AN=BM。
(2)证明:∵△CMB≌△CAN,∴∠ANC=∠MBC。又∵∠MCN=∠FCB=60°,
BC=CN,
∴△ECN≌△FCB,∴CE=CF。
又∵∠ECF=60°,∴△ECF是等边三角形。
(3)如图②所示,(1)小题的结论仍然成立,(2)小题不成立。
谢 谢
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
