人教版六年级数学上册 比的应用(例2) 课件(共35张PPT)
文档属性
| 名称 | 人教版六年级数学上册 比的应用(例2) 课件(共35张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 15:34:22 | ||
图片预览





文档简介
(共35张PPT)
六年级上册—人教版—数学—第四单元
比的应用(例2)
1. 在解决实际问题的过程中,进一步体会比的意义。
2. 能运用比的意义解决有关按比分配的实际问题,提
高解决问题的能力。
3. 在解决过程中体会数学知识之间的内在联系。
学习目标
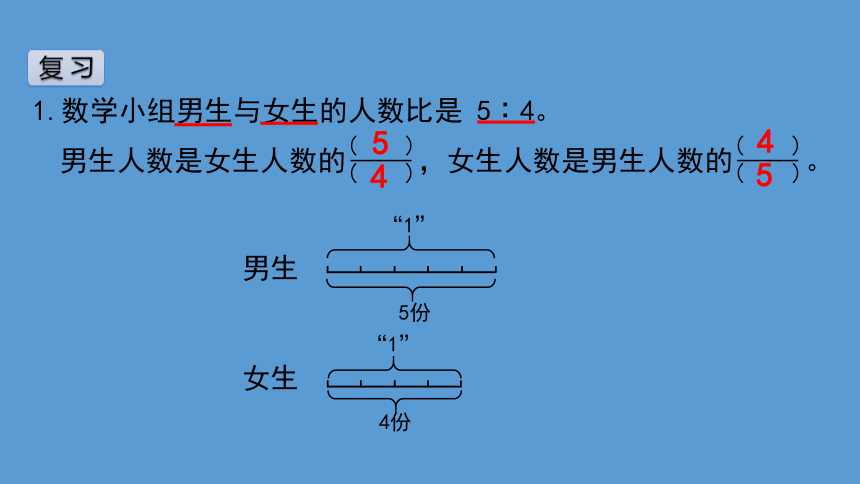
1.数学小组男生与女生的人数比是 5∶4。
男生人数是女生人数的 ,女生人数是男生人数的 。
女生
男生
复 习
“1”
4份
5份
“1”
( )
( )
( )
( )
5
4
4
5
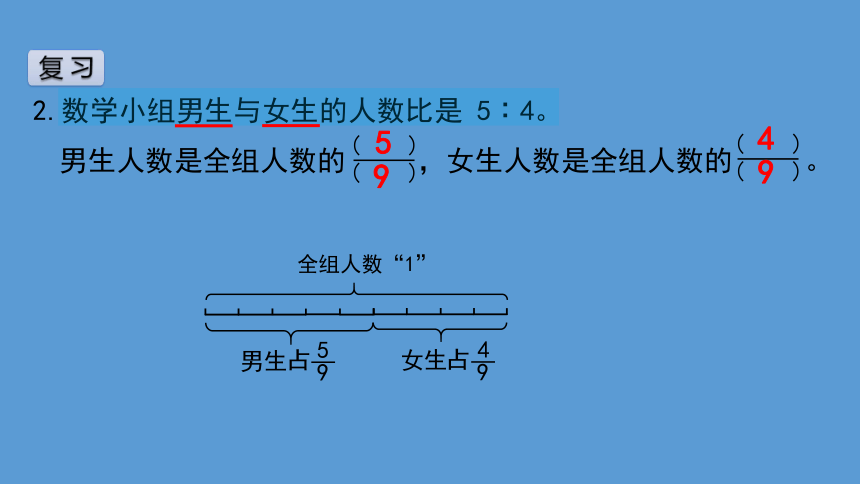
2.数学小组男生与女生的人数比是 5∶4。
全组人数“1”
男生
占
5
9
女生
占
4
9
复 习
男生人数是全组人数的 ,女生人数是全组人数的 。
( )
( )
( )
( )
5
9
4
9
数学小组男生与女生人数的比是 5∶4。
女生人数是男生人数的 。
4
5
男生人数是女生人数的 ,
5
4
男生人数是全组人数的 ,
5
9
女生人数是全组人数的 。
4
9
复 习
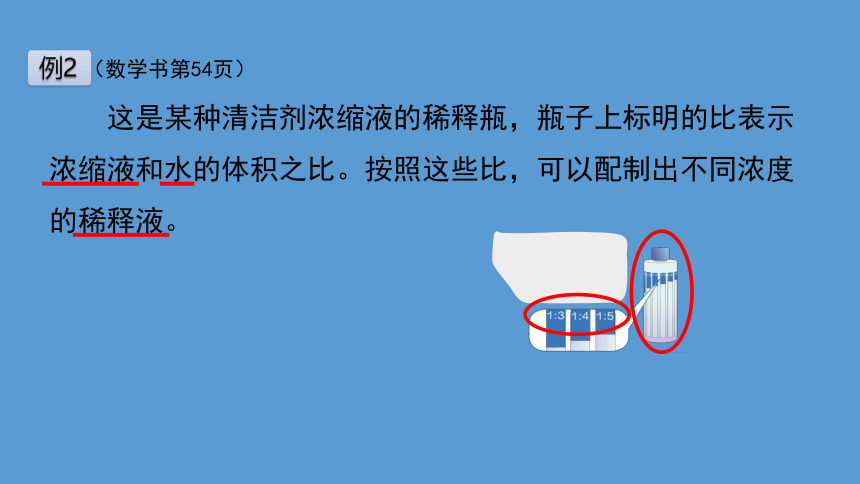
这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。
(数学书第54页)
例2
这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。
稀
释
液
清洁剂
(数学书第54页)
例2
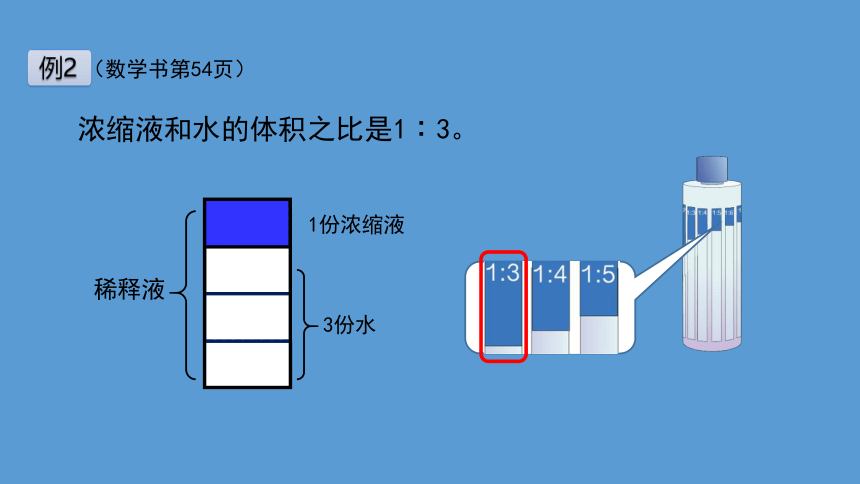
1份浓缩液
3份水
浓缩液和水的体积之比是1∶3。
稀释液
(数学书第54页)
例2
(数学书第54页)
例2
阅读与理解
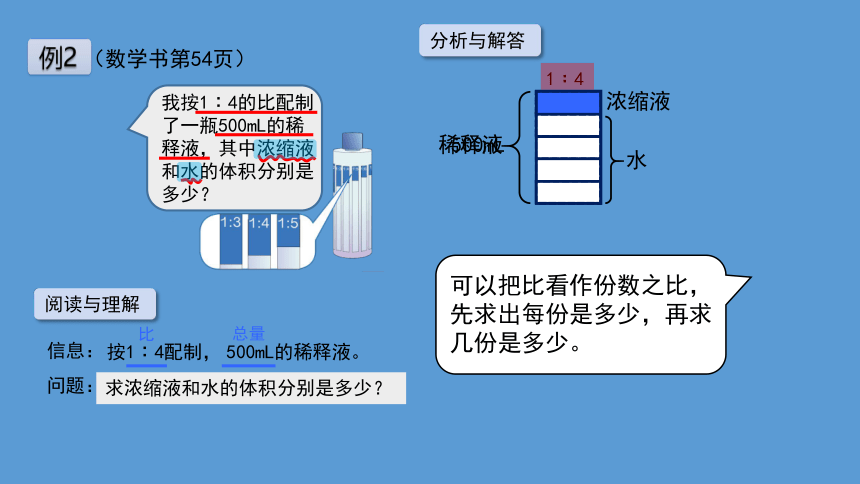
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
稀释液
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
信息:
问题:
按1∶4配制,
500mL的稀释液。
求浓缩液和水的体积分别是多少?
(数学书第54页)
例2
浓缩液
水
500mL
比
总量
阅读与理解
分析与解答
可以把比看作份数之比,先求出每份是多少,再求几份是多少。
1﹕4
信息:
问题:
按1∶4配制,
500mL的稀释液。
求浓缩液和水的体积分别是多少?
(数学书第54页)
例2
浓缩液
水
500mL
比
总量
阅读与理解
分析与解答
1﹕4
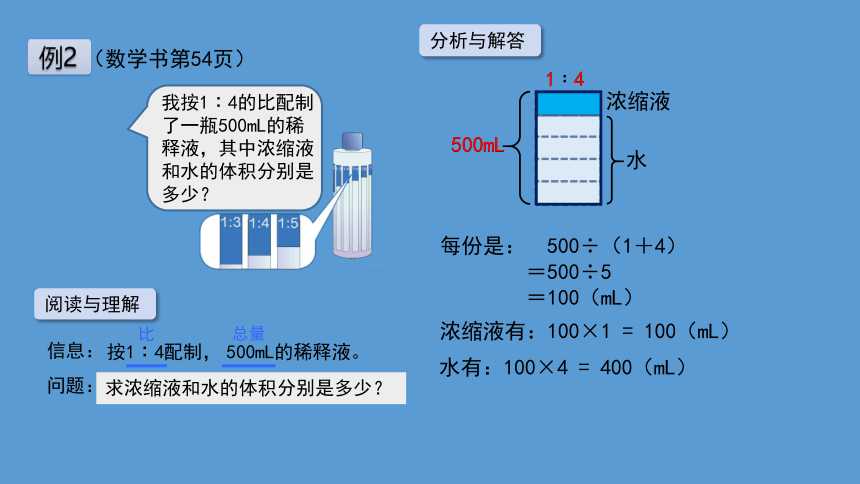
每份是: 500÷(1+4)
=500÷5
=100(mL)
浓缩液有:100×1 = 100(mL)
水有:100×4 = 400(mL)
1
4
500mL
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
( )
( )
占
信息:
问题:
按1∶4配制,
500mL的稀释液。
求浓缩液和水的体积分别是多少?
(数学书第54页)
例2
浓缩液
水
500mL
比
总量
阅读与理解
分析与解答
1﹕4
( )
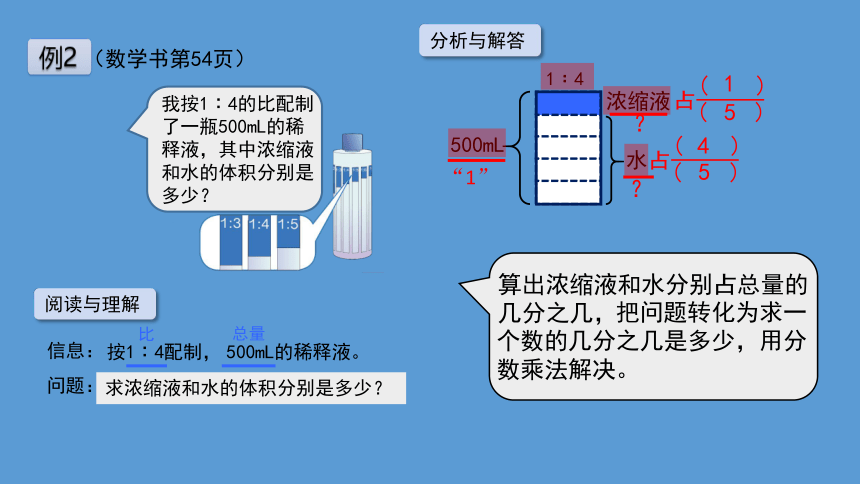
( )
占
5
4
1
5
“1”
?
?
把问题转化为求一个数的几分之几是多少,用分数乘法解决。
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
信息:
问题:
按1∶4配制,
500mL的稀释液。
求浓缩液和水的体积分别是多少?
(数学书第54页)
例2
浓缩液
水
500mL
比
总量
阅读与理解
分析与解答
1﹕4
浓缩液有:500× = 100(mL)
1+4
1
水有:500× = 400(mL)
1+4
4
1
1
4
4
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
(数学书第54页)
例2
回顾与反思
答:浓缩液有100mL,水有400mL。
?
浓缩液有:100×1 = 100(mL)
水有:100×4 = 400(mL)
答:浓缩液有100mL,水有400mL。
每份是:500÷(1 + 4 )
=500÷5
=100(mL)
浓缩液有:500× = 100(mL)
1+4
1
水有:500× = 400(mL)
1+4
4
答:浓缩液有100mL,水有400mL。
浓缩液与水的体积比是1∶4
浓缩液
水
500mL
1﹕4
比 一 比
方法一
方法二
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
(数学书第54页)
学习回顾
信息:
问题:
按1∶4配制,
500mL的稀释液。
求浓缩液和水的体积分别是多少?
比
总量
阅读与理解
浓缩液与水的体积比是1∶4
浓缩液
水
500mL
分析与解答
浓缩液有:500× = 100(mL)
1
1+4
水有:500× = 400(mL)
1+4
4
答:浓缩液有100mL,水有400mL。
回顾与反思
我把浓缩液与水的体积相加,
即100 + 400 = 500(mL),
正好等于稀释液的500mL。
学校图书馆新进了450本图书,按4﹕5分给五年级和六年级,这两个年级各分得多少本图书?
做 一 做
比
总量
?
?
450本
五年级
六年级
5
9
占
4
9
占
五年级有:450× =200(本)
4
4+5
六年级有:450× =250(本)
5
4+5
4份
5份
五年级有:50×4 = 200(本)
“1”
六年级有:50×5 = 250(本)
每份是:450÷(4+5)
=450÷9
=50(本)
方法一
方法二
答:五年级分得200本,六年级分得250本。
1.晓琳带了30元钱去买文具,用去的钱与余下的钱的比是
3︰7,晓琳用去了总钱数的 ,用去了( )元。
用去的︰余下的
练 一 练
( )
( )
10
3
9
总钱数
30元
用去的
余下的
10
3
占
“1”
用去了:30× =9(元)
3
3+7
2.某种果汁饮料是用2份纯果汁和3份水配制而成的,要配制一瓶
500mL的果汁饮料,纯果汁的质量是多少毫升?
正确列式是( )。(单选)
③
2∶3
①500×
3
2
② 500÷
3
2
③ 500×
2+3
2
④ 500÷
2+3
2
练 一 练
选择正确答案的序号填在括号里。
男婴人数:女婴人数
3.某妇产医院上月新生婴儿303名,男女婴儿人数之比是 51:50。上月新生男、女婴儿各有多少人?
(数学书第55页第1题)
练 一 练
答:上月新生男婴儿有153人,女婴儿有150人。
女婴人数: 303×
=303×
=150(人)
50
101
51+50
50
男婴人数: 303×
=303×
=153(人)
51+50
51
101
51
?
?
4.学校把栽70棵树的任务按照六年级三个班的人数分配给各班,一
班有46人,二班有44人,三班有50人。三个班各应栽多少棵树?
(数学书第55页第4题)
一班∶二班∶三班
=46∶44∶50
=23∶22∶25
练 一 练
一班:70×
= 70×
= 23(棵)
23+22+25
23
70
23
二班:70×
= 70×
= 22(棵)
23+22+25
22
70
22
三班:70×
= 70×
= 25(棵)
23+22+25
25
70
25
答:一班应栽23棵,二班应栽22棵,三班应栽25棵。
练 一 练
5.(1)一个三角形,三个内角的度数比是4︰5︰9,这个三角形三个
内角分别是多少度?这是一个什么三角形?
(2)一个等腰三角形的顶角和它的一个底角的度数比是 1︰4,这
个等腰三角形的顶角和底角分别是多少度?
3:180°×
=180°×
=90°
4+5+9
9
18
9
5.(1)一个三角形,三个内角的度数比是4︰5︰9,这个三角形三个
内角分别是多少度?这是一个什么三角形?
练 一 练
三角形内角和的度数是 。
180°
?
1:180°×
=180°×
=40°
4+5+9
4
18
4
2:180°×
=180°×
=50°
4+5+9
5
18
5
答:这个三角形三个内角分别是40°、50°和90°。这是一个直角三角形。
等腰三角形的两个底角相等
练 一 练
5.(2)一个等腰三角形的顶角和它的一个底角的度数比是 1︰4,这
个等腰三角形的顶角和底角分别是多少度?
等腰三角形中有 个顶角, 个底角。
1
顶角
底角
底角
2
顶角︰底角︰底角=1︰4︰4
顶角:180°×
=180°×
=20°
1+4+4
1
9
1
底角:180°×
=180°×
=80°
1+4+4
4
9
4
答:这个等腰三角形的顶角是20°,底角是80°。
课堂小结
已知几个量的和,及这几个量的比,分别求这几个量。
根据比求出总份数,理解为各部分占总数量的几分之几,进而转化为分数乘法进行解答。
检验时,要同时符合题目的已知条件。
课后作业:
1.复习数学书第54页例2。
2.完成数学书第55页第2、3题。
六年级上册—人教版—数学—第四单元
比的应用(例2) 答疑
在工业生产和日常生活中,常常要把一个总量按照一定的比进行分配,这种分配的方法,通常叫做按比分配。
答 疑
什么是按比分配?
按比分配在生活中有什么用?
按一定的比分配的方法在生活中应用非常广泛。
水泥、沙子和石子来搅拌混凝土。
按比分配在生活中有什么用?
例如:工程队要用水泥、沙子和石子共20t来搅拌混凝土,三种原料分别需要多少吨?
(数学书第56页第10题)
水泥:20× =4(t)
2+3+5
2
沙子:20× =6(t)
2+3+5
3
答:需要水泥4吨,沙子6吨,石子10吨。
水泥、沙子和石子的比是2︰3︰5。
2+3+5
5
石子:20× =10(t)
按比分配在生活中有什么用?
小红、小明和晓军三位朋友合租一辆车,大家约定分摊车费,小红在全程的 处下车,到了全程的 处小明也下车了,最后晓军一个人坐到终点,共付48元。请问小红、小明各应付给晓军多少钱?
3
1
3
2
按比分配在生活中有什么用?
小红坐了全程的 ,
3
1
小明坐了全程的 ,
3
2
3
1
︰ ︰1
3
2
= 1︰2︰3
根据这几个信息,就可以求出他们坐车的路程比。
晓军坐完全程,
小红、小明和晓军三位朋友合租一辆车,大家约定分摊车费,小红在全程的 处下车,到了全程的 处小明也下车了,最后晓军一个人坐到终点,共付48元。请问小红、小明各应付给晓军多少钱?
3
1
3
2
3
1
︰ ︰1
3
2
= 1︰2︰3
小红:48× =8(元)
1+2+3
1
小明:48× =16(元)
1+2+3
2
答:小红应付给晓军8元,小明应付给晓军16元。
按比分配在生活中有什么用?
小红、小明和晓军三位朋友合租一辆车,大家约定分摊车费,小红在全程的 处下车,到了全程的 处小明也下车了,最后晓军一个人坐到终点,共付48元。请问小红、小明各应付给晓军多少钱?
3
1
3
2
理解为把10颗糖平均分成2份,两人各占其中的1份。
平均分就是按一定的比分配的一种特殊例子。
把10颗糖按 1︰1 分给小明和小红,
2
1
每人分得总数的 。
谢 谢 观 看!
六年级上册—人教版—数学—第四单元
比的应用(例2)
1. 在解决实际问题的过程中,进一步体会比的意义。
2. 能运用比的意义解决有关按比分配的实际问题,提
高解决问题的能力。
3. 在解决过程中体会数学知识之间的内在联系。
学习目标
1.数学小组男生与女生的人数比是 5∶4。
男生人数是女生人数的 ,女生人数是男生人数的 。
女生
男生
复 习
“1”
4份
5份
“1”
( )
( )
( )
( )
5
4
4
5
2.数学小组男生与女生的人数比是 5∶4。
全组人数“1”
男生
占
5
9
女生
占
4
9
复 习
男生人数是全组人数的 ,女生人数是全组人数的 。
( )
( )
( )
( )
5
9
4
9
数学小组男生与女生人数的比是 5∶4。
女生人数是男生人数的 。
4
5
男生人数是女生人数的 ,
5
4
男生人数是全组人数的 ,
5
9
女生人数是全组人数的 。
4
9
复 习
这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。
(数学书第54页)
例2
这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。
稀
释
液
清洁剂
(数学书第54页)
例2
1份浓缩液
3份水
浓缩液和水的体积之比是1∶3。
稀释液
(数学书第54页)
例2
(数学书第54页)
例2
阅读与理解
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
稀释液
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
信息:
问题:
按1∶4配制,
500mL的稀释液。
求浓缩液和水的体积分别是多少?
(数学书第54页)
例2
浓缩液
水
500mL
比
总量
阅读与理解
分析与解答
可以把比看作份数之比,先求出每份是多少,再求几份是多少。
1﹕4
信息:
问题:
按1∶4配制,
500mL的稀释液。
求浓缩液和水的体积分别是多少?
(数学书第54页)
例2
浓缩液
水
500mL
比
总量
阅读与理解
分析与解答
1﹕4
每份是: 500÷(1+4)
=500÷5
=100(mL)
浓缩液有:100×1 = 100(mL)
水有:100×4 = 400(mL)
1
4
500mL
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
( )
( )
占
信息:
问题:
按1∶4配制,
500mL的稀释液。
求浓缩液和水的体积分别是多少?
(数学书第54页)
例2
浓缩液
水
500mL
比
总量
阅读与理解
分析与解答
1﹕4
( )
( )
占
5
4
1
5
“1”
?
?
把问题转化为求一个数的几分之几是多少,用分数乘法解决。
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
信息:
问题:
按1∶4配制,
500mL的稀释液。
求浓缩液和水的体积分别是多少?
(数学书第54页)
例2
浓缩液
水
500mL
比
总量
阅读与理解
分析与解答
1﹕4
浓缩液有:500× = 100(mL)
1+4
1
水有:500× = 400(mL)
1+4
4
1
1
4
4
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
(数学书第54页)
例2
回顾与反思
答:浓缩液有100mL,水有400mL。
?
浓缩液有:100×1 = 100(mL)
水有:100×4 = 400(mL)
答:浓缩液有100mL,水有400mL。
每份是:500÷(1 + 4 )
=500÷5
=100(mL)
浓缩液有:500× = 100(mL)
1+4
1
水有:500× = 400(mL)
1+4
4
答:浓缩液有100mL,水有400mL。
浓缩液与水的体积比是1∶4
浓缩液
水
500mL
1﹕4
比 一 比
方法一
方法二
我按1︰4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
(数学书第54页)
学习回顾
信息:
问题:
按1∶4配制,
500mL的稀释液。
求浓缩液和水的体积分别是多少?
比
总量
阅读与理解
浓缩液与水的体积比是1∶4
浓缩液
水
500mL
分析与解答
浓缩液有:500× = 100(mL)
1
1+4
水有:500× = 400(mL)
1+4
4
答:浓缩液有100mL,水有400mL。
回顾与反思
我把浓缩液与水的体积相加,
即100 + 400 = 500(mL),
正好等于稀释液的500mL。
学校图书馆新进了450本图书,按4﹕5分给五年级和六年级,这两个年级各分得多少本图书?
做 一 做
比
总量
?
?
450本
五年级
六年级
5
9
占
4
9
占
五年级有:450× =200(本)
4
4+5
六年级有:450× =250(本)
5
4+5
4份
5份
五年级有:50×4 = 200(本)
“1”
六年级有:50×5 = 250(本)
每份是:450÷(4+5)
=450÷9
=50(本)
方法一
方法二
答:五年级分得200本,六年级分得250本。
1.晓琳带了30元钱去买文具,用去的钱与余下的钱的比是
3︰7,晓琳用去了总钱数的 ,用去了( )元。
用去的︰余下的
练 一 练
( )
( )
10
3
9
总钱数
30元
用去的
余下的
10
3
占
“1”
用去了:30× =9(元)
3
3+7
2.某种果汁饮料是用2份纯果汁和3份水配制而成的,要配制一瓶
500mL的果汁饮料,纯果汁的质量是多少毫升?
正确列式是( )。(单选)
③
2∶3
①500×
3
2
② 500÷
3
2
③ 500×
2+3
2
④ 500÷
2+3
2
练 一 练
选择正确答案的序号填在括号里。
男婴人数:女婴人数
3.某妇产医院上月新生婴儿303名,男女婴儿人数之比是 51:50。上月新生男、女婴儿各有多少人?
(数学书第55页第1题)
练 一 练
答:上月新生男婴儿有153人,女婴儿有150人。
女婴人数: 303×
=303×
=150(人)
50
101
51+50
50
男婴人数: 303×
=303×
=153(人)
51+50
51
101
51
?
?
4.学校把栽70棵树的任务按照六年级三个班的人数分配给各班,一
班有46人,二班有44人,三班有50人。三个班各应栽多少棵树?
(数学书第55页第4题)
一班∶二班∶三班
=46∶44∶50
=23∶22∶25
练 一 练
一班:70×
= 70×
= 23(棵)
23+22+25
23
70
23
二班:70×
= 70×
= 22(棵)
23+22+25
22
70
22
三班:70×
= 70×
= 25(棵)
23+22+25
25
70
25
答:一班应栽23棵,二班应栽22棵,三班应栽25棵。
练 一 练
5.(1)一个三角形,三个内角的度数比是4︰5︰9,这个三角形三个
内角分别是多少度?这是一个什么三角形?
(2)一个等腰三角形的顶角和它的一个底角的度数比是 1︰4,这
个等腰三角形的顶角和底角分别是多少度?
3:180°×
=180°×
=90°
4+5+9
9
18
9
5.(1)一个三角形,三个内角的度数比是4︰5︰9,这个三角形三个
内角分别是多少度?这是一个什么三角形?
练 一 练
三角形内角和的度数是 。
180°
?
1:180°×
=180°×
=40°
4+5+9
4
18
4
2:180°×
=180°×
=50°
4+5+9
5
18
5
答:这个三角形三个内角分别是40°、50°和90°。这是一个直角三角形。
等腰三角形的两个底角相等
练 一 练
5.(2)一个等腰三角形的顶角和它的一个底角的度数比是 1︰4,这
个等腰三角形的顶角和底角分别是多少度?
等腰三角形中有 个顶角, 个底角。
1
顶角
底角
底角
2
顶角︰底角︰底角=1︰4︰4
顶角:180°×
=180°×
=20°
1+4+4
1
9
1
底角:180°×
=180°×
=80°
1+4+4
4
9
4
答:这个等腰三角形的顶角是20°,底角是80°。
课堂小结
已知几个量的和,及这几个量的比,分别求这几个量。
根据比求出总份数,理解为各部分占总数量的几分之几,进而转化为分数乘法进行解答。
检验时,要同时符合题目的已知条件。
课后作业:
1.复习数学书第54页例2。
2.完成数学书第55页第2、3题。
六年级上册—人教版—数学—第四单元
比的应用(例2) 答疑
在工业生产和日常生活中,常常要把一个总量按照一定的比进行分配,这种分配的方法,通常叫做按比分配。
答 疑
什么是按比分配?
按比分配在生活中有什么用?
按一定的比分配的方法在生活中应用非常广泛。
水泥、沙子和石子来搅拌混凝土。
按比分配在生活中有什么用?
例如:工程队要用水泥、沙子和石子共20t来搅拌混凝土,三种原料分别需要多少吨?
(数学书第56页第10题)
水泥:20× =4(t)
2+3+5
2
沙子:20× =6(t)
2+3+5
3
答:需要水泥4吨,沙子6吨,石子10吨。
水泥、沙子和石子的比是2︰3︰5。
2+3+5
5
石子:20× =10(t)
按比分配在生活中有什么用?
小红、小明和晓军三位朋友合租一辆车,大家约定分摊车费,小红在全程的 处下车,到了全程的 处小明也下车了,最后晓军一个人坐到终点,共付48元。请问小红、小明各应付给晓军多少钱?
3
1
3
2
按比分配在生活中有什么用?
小红坐了全程的 ,
3
1
小明坐了全程的 ,
3
2
3
1
︰ ︰1
3
2
= 1︰2︰3
根据这几个信息,就可以求出他们坐车的路程比。
晓军坐完全程,
小红、小明和晓军三位朋友合租一辆车,大家约定分摊车费,小红在全程的 处下车,到了全程的 处小明也下车了,最后晓军一个人坐到终点,共付48元。请问小红、小明各应付给晓军多少钱?
3
1
3
2
3
1
︰ ︰1
3
2
= 1︰2︰3
小红:48× =8(元)
1+2+3
1
小明:48× =16(元)
1+2+3
2
答:小红应付给晓军8元,小明应付给晓军16元。
按比分配在生活中有什么用?
小红、小明和晓军三位朋友合租一辆车,大家约定分摊车费,小红在全程的 处下车,到了全程的 处小明也下车了,最后晓军一个人坐到终点,共付48元。请问小红、小明各应付给晓军多少钱?
3
1
3
2
理解为把10颗糖平均分成2份,两人各占其中的1份。
平均分就是按一定的比分配的一种特殊例子。
把10颗糖按 1︰1 分给小明和小红,
2
1
每人分得总数的 。
谢 谢 观 看!
