人教版六年级数学上册 圆的周长练习课 课件(共20张PPT)
文档属性
| 名称 | 人教版六年级数学上册 圆的周长练习课 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 15:38:06 | ||
图片预览







文档简介
(共20张PPT)
六年级—人教版—数学—第五单元
圆的周长练习课
1.加深对圆的周长的理解,进一步熟练圆的周长的计算。
2.通过读一读、画一画、想一想等多种方法,结合生活情境分析理解题意,独立完成多种问题情境的练习。
3.提高解决实际问题的综合能力。
学习目标
1.箍圆桌边缘一周铁皮的长度。
桌面
2.车轮走一圈的路程。
3.时钟的分针尖端走一周的长度。
知识回顾
C = πd
C = 2πr
圆周率 π
知识回顾
1.一个圆的直径是4厘米,它的周长是多少厘米?
C=πd
3.14 ×4=12.56(厘米)
2.一个圆的半径是2厘米,它的周长是多少厘米?
C=2πr
3.14 ×2×2=12.56(厘米)
基本练习
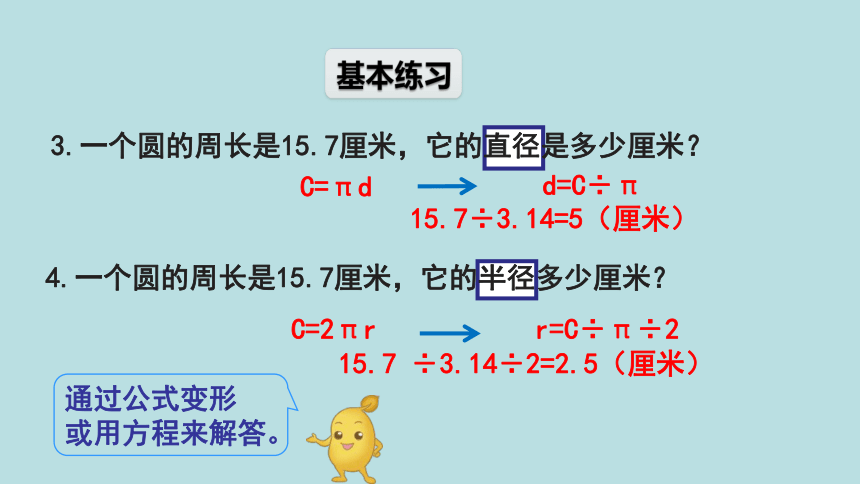
3.一个圆的周长是15.7厘米,它的直径是多少厘米?
d=C÷π
15.7÷3.14=5(厘米)
4.一个圆的周长是15.7厘米,它的半径多少厘米?
r=C÷π÷2
15.7 ÷3.14÷2=2.5(厘米)
C=πd
C=2πr
基本练习
通过公式变形
或用方程来解答。
1.小红量得一个古代建筑中的大红圆柱的周长是3.77m,这个圆柱的直径是多少m (得数保留一位小数。)
已知:C=3.77m 求: d = m
3.77÷3.14≈1.2(m)
答:这个圆柱的直径是1.2米。
C=πd
d=C÷π
(数学书第65页第3题)
综合练习
2.一只挂钟的分针长20cm ,经过30分钟后,分针的尖端所走的路程是多少厘米?经过45分钟呢?
分针的尖端走一圈的路程就是以分针长度为( )的圆的周长。
分针的尖端走30分钟的路程是一圈的( )。
半径
一半
半径
一半
答:经过30分钟后,分针的尖端所走的路程是62.8厘米。
(数学书第65页第4题)
综合练习
分针的尖端走一圈的路程:C =2πr
=2×3.14 ×20
=6.28×20
=125.6(cm)
分针的尖端走30分钟的路程:125.6 ÷2 = 62.8(cm)
20cm
2.一只挂钟的分针长20cm ,经过30分钟后,分针的尖端所走的路程是多少厘米?经过45分钟呢?
分针的尖端走45分钟的路程是一圈的( )。
答:经过45分钟后,分针的尖端所走的路程是94.2厘米。
(数学书第65页第4题)
综合练习
分针的尖端走一圈的路程是125.6cm。
= 94.2(cm)
分针的尖端走45分钟的路程:125.6×
20cm
看图填空(单位:cm)。
(1)
正方形的周长是( )cm,
圆的周长是( )cm。
直径
2×2×4=16(㎝)
2×3.14×2=12.56(㎝)
(数学书第66页第7题)
沟通练习
正方形里面最大的圆,
它的直径等于( )。
正方形的边长
16
12.56
看图填空(单位:cm)。
(2)
其中一个圆的周长是( )cm,
长方形的周长是( )cm。
2×3.14×1.5=9.42(㎝)
(1.5×5+1.5×2)×2=21(㎝)
(数学书第66页第7题)
沟通练习
长方形的宽相当于( )。
长方形的长相当于( )。
圆的直径
圆的半径的5倍
9.42
21
利用图示、标注等,结合具体情境分析数据间的关系是关键;
熟练掌握公式是前提;
单位统一、计算正确、完整作答等是要领。
认真分析 灵活运用
课堂总结
1.复习圆的周长内容。
2.数学书第65页第2题,第66页第9题。
课后作业
六年级—人教版—数学—第五单元
圆的周长练习课答疑
1.如何理解“圆沿直线滚动一周所经过的距离就是这个圆的周长。”
答 疑
1.如何理解“圆沿直线滚动一周所经过的距离就是这个圆的周长。”
细线绕圆一周,随着滚动的推进细线在平面展开成一条直线,细线长就是圆周长,直线的长度就是圆滚动一周的所经过的距离。
答 疑
杂技演员表演独轮车走钢丝,车轮的直径为40cm,要骑过50.24m长的钢丝,车轮大约要转动多少周?
独轮车沿钢丝滚动一周所经过的距离就是这个独轮车车轮的( )。
转化单位: 125.6㎝=1.256m
C =πd
转动的周数: 50.24÷1.256=40(周)
答:车轮大约要转动40周。
车轮的周长: 40×3.14=125.6(㎝)
周长
周长
(数学书第65页第6题)
答 疑
2.判断对错,对的画“√”,错的画“X”。
X
X
(1)圆的直径增加a厘米,那么圆的周长也增加a厘米。 ( ) ( )
X
根据 C=πd
原来圆的直径: d 原来圆的周长:πd
现在圆的直径: d+a 现在圆的周长:π(d+a)=πd +πa
答 疑
解析:
增加的厘米数: πd +πa-πd =πa
所以,圆的直径增加a厘米,圆的周长增加(πa)厘米。
2.判断对错,对的画“√”,错的画“X”。
X
X
(2)圆的直径扩大到原来的a倍,那么圆的周长也扩大到原来的 a倍。( )
√
答 疑
根据 C=πd
原来圆的直径: d 原来圆的周长: πd
现在圆的直径: da 现在圆的周长: πda
解析:
扩大到原来的倍数: πda÷(πd)= a
所以,圆的直径扩大到原来的a倍,那么圆的周长也扩大到原来的 a倍。
谢谢观看
再 见
六年级—人教版—数学—第五单元
圆的周长练习课
1.加深对圆的周长的理解,进一步熟练圆的周长的计算。
2.通过读一读、画一画、想一想等多种方法,结合生活情境分析理解题意,独立完成多种问题情境的练习。
3.提高解决实际问题的综合能力。
学习目标
1.箍圆桌边缘一周铁皮的长度。
桌面
2.车轮走一圈的路程。
3.时钟的分针尖端走一周的长度。
知识回顾
C = πd
C = 2πr
圆周率 π
知识回顾
1.一个圆的直径是4厘米,它的周长是多少厘米?
C=πd
3.14 ×4=12.56(厘米)
2.一个圆的半径是2厘米,它的周长是多少厘米?
C=2πr
3.14 ×2×2=12.56(厘米)
基本练习
3.一个圆的周长是15.7厘米,它的直径是多少厘米?
d=C÷π
15.7÷3.14=5(厘米)
4.一个圆的周长是15.7厘米,它的半径多少厘米?
r=C÷π÷2
15.7 ÷3.14÷2=2.5(厘米)
C=πd
C=2πr
基本练习
通过公式变形
或用方程来解答。
1.小红量得一个古代建筑中的大红圆柱的周长是3.77m,这个圆柱的直径是多少m (得数保留一位小数。)
已知:C=3.77m 求: d = m
3.77÷3.14≈1.2(m)
答:这个圆柱的直径是1.2米。
C=πd
d=C÷π
(数学书第65页第3题)
综合练习
2.一只挂钟的分针长20cm ,经过30分钟后,分针的尖端所走的路程是多少厘米?经过45分钟呢?
分针的尖端走一圈的路程就是以分针长度为( )的圆的周长。
分针的尖端走30分钟的路程是一圈的( )。
半径
一半
半径
一半
答:经过30分钟后,分针的尖端所走的路程是62.8厘米。
(数学书第65页第4题)
综合练习
分针的尖端走一圈的路程:C =2πr
=2×3.14 ×20
=6.28×20
=125.6(cm)
分针的尖端走30分钟的路程:125.6 ÷2 = 62.8(cm)
20cm
2.一只挂钟的分针长20cm ,经过30分钟后,分针的尖端所走的路程是多少厘米?经过45分钟呢?
分针的尖端走45分钟的路程是一圈的( )。
答:经过45分钟后,分针的尖端所走的路程是94.2厘米。
(数学书第65页第4题)
综合练习
分针的尖端走一圈的路程是125.6cm。
= 94.2(cm)
分针的尖端走45分钟的路程:125.6×
20cm
看图填空(单位:cm)。
(1)
正方形的周长是( )cm,
圆的周长是( )cm。
直径
2×2×4=16(㎝)
2×3.14×2=12.56(㎝)
(数学书第66页第7题)
沟通练习
正方形里面最大的圆,
它的直径等于( )。
正方形的边长
16
12.56
看图填空(单位:cm)。
(2)
其中一个圆的周长是( )cm,
长方形的周长是( )cm。
2×3.14×1.5=9.42(㎝)
(1.5×5+1.5×2)×2=21(㎝)
(数学书第66页第7题)
沟通练习
长方形的宽相当于( )。
长方形的长相当于( )。
圆的直径
圆的半径的5倍
9.42
21
利用图示、标注等,结合具体情境分析数据间的关系是关键;
熟练掌握公式是前提;
单位统一、计算正确、完整作答等是要领。
认真分析 灵活运用
课堂总结
1.复习圆的周长内容。
2.数学书第65页第2题,第66页第9题。
课后作业
六年级—人教版—数学—第五单元
圆的周长练习课答疑
1.如何理解“圆沿直线滚动一周所经过的距离就是这个圆的周长。”
答 疑
1.如何理解“圆沿直线滚动一周所经过的距离就是这个圆的周长。”
细线绕圆一周,随着滚动的推进细线在平面展开成一条直线,细线长就是圆周长,直线的长度就是圆滚动一周的所经过的距离。
答 疑
杂技演员表演独轮车走钢丝,车轮的直径为40cm,要骑过50.24m长的钢丝,车轮大约要转动多少周?
独轮车沿钢丝滚动一周所经过的距离就是这个独轮车车轮的( )。
转化单位: 125.6㎝=1.256m
C =πd
转动的周数: 50.24÷1.256=40(周)
答:车轮大约要转动40周。
车轮的周长: 40×3.14=125.6(㎝)
周长
周长
(数学书第65页第6题)
答 疑
2.判断对错,对的画“√”,错的画“X”。
X
X
(1)圆的直径增加a厘米,那么圆的周长也增加a厘米。 ( ) ( )
X
根据 C=πd
原来圆的直径: d 原来圆的周长:πd
现在圆的直径: d+a 现在圆的周长:π(d+a)=πd +πa
答 疑
解析:
增加的厘米数: πd +πa-πd =πa
所以,圆的直径增加a厘米,圆的周长增加(πa)厘米。
2.判断对错,对的画“√”,错的画“X”。
X
X
(2)圆的直径扩大到原来的a倍,那么圆的周长也扩大到原来的 a倍。( )
√
答 疑
根据 C=πd
原来圆的直径: d 原来圆的周长: πd
现在圆的直径: da 现在圆的周长: πda
解析:
扩大到原来的倍数: πda÷(πd)= a
所以,圆的直径扩大到原来的a倍,那么圆的周长也扩大到原来的 a倍。
谢谢观看
再 见
