人教版六年级数学上册 扇形 课件(共38张PPT)
文档属性
| 名称 | 人教版六年级数学上册 扇形 课件(共38张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 00:00:00 | ||
图片预览








文档简介
(共38张PPT)
六年级—人教版—数学—第五单元
扇形
1.知道扇形是从圆中产生,知道扇形各部分的名称(弧、半径、圆心角),会判断扇形及其圆心角。 2.通过回忆生活中扇形物品,抽象扇形的数学概念,掌握研究问题的一般方法 。 3.积累数学活动经验。
学习目标
生活中的扇形
生活中的扇形
A
B
弧
图上A、B两点之间的部分叫做弧。
读作“弧AB”。
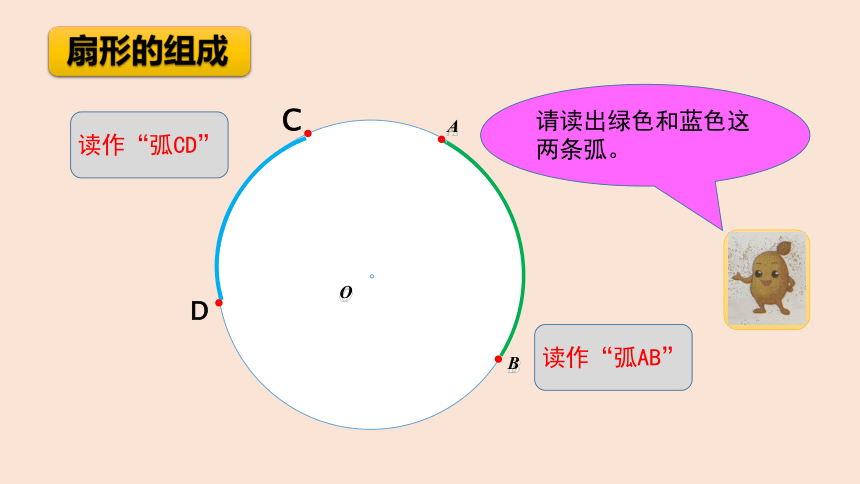
扇形的组成
O
A
B
请读出绿色和蓝色这两条弧。
读作“弧CD”
读作“弧AB”
扇形的组成
C
D
A
B
O
半径
半径
弧
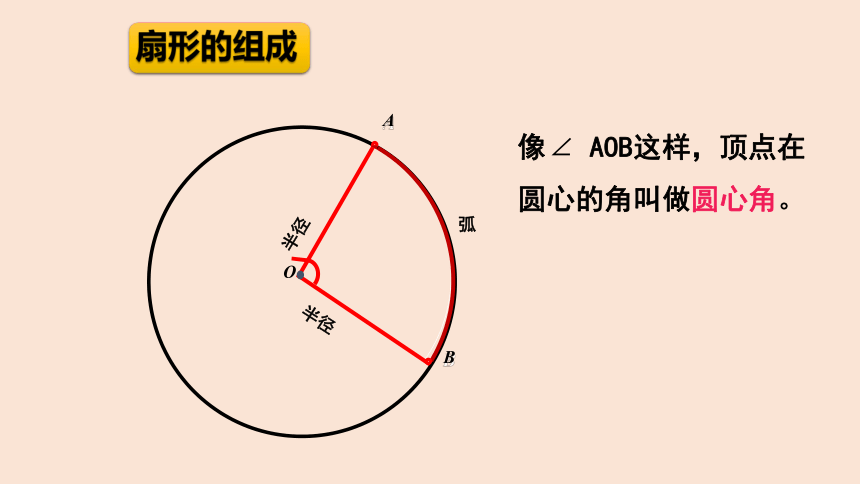
像∠ AOB这样,顶点在圆心的角叫做圆心角。
扇形的组成
下面各图中,哪些角是圆心角?(书:76页第2题)
√
√
练习一
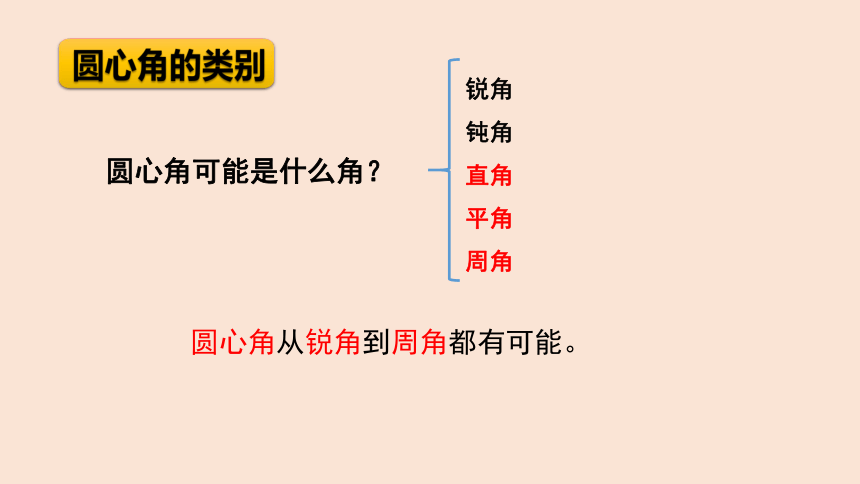
圆心角的类别
圆心角可能是什么角?
锐角
钝角
平角
直角
270°
周角
圆心角的类别
圆心角可能是什么角?
锐角
钝角
直角
平角
周角
圆心角从锐角到周角都有可能。
A
B
O
半径
半径
弧
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
扇形的定义
半径
半径
弧
圆心角
O
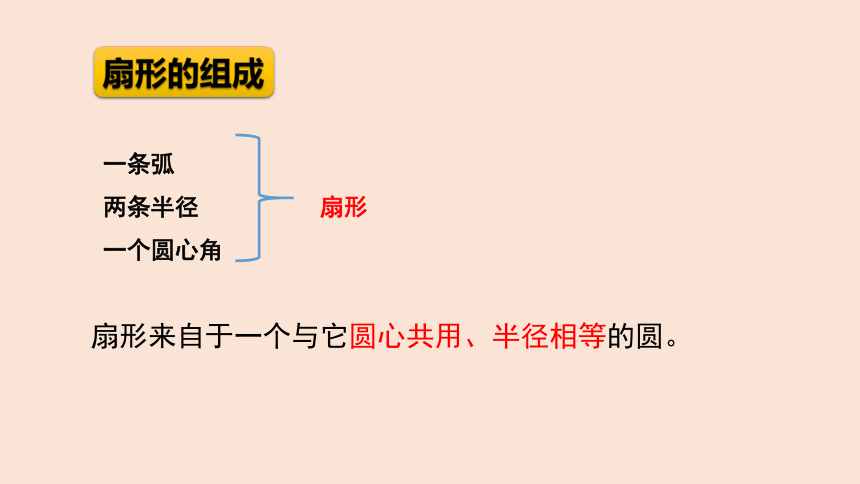
扇形的组成
一条弧
两条半径 扇形
一个圆心角
扇形来自于一个与它圆心共用、半径相等的圆。
在同一个圆里,扇形的大小与什么有关系呢?
在同一个圆里,扇形的大小与圆心角有关。
1
3
4
在同圆里,圆心角越大,扇形就越大,圆心角越小,扇形就越小。
扇形的大小
60°
90°
30°
180°
1
2
.
在同一个圆里,扇形的大小与什么有关系呢?
3
扇形的大小
60°
90°
30°
180°
1
2
在同圆里,圆心角扩大到原来的几倍,扇形面积也扩大到原来的几倍。
4
r=2cm
r=3cm
猜猜下面两个扇形的面积,谁大谁小?
扇形的大小
.
.
r=2cm
r=3cm
圆心角相等,半径越长(短),
扇形面积越大(小)。
扇形的大小
.
.
影响扇形大小的条件有两个:一是圆心角的大小,二是半径的长短。
观察下面的扇形,想想它们的大小与什么有关?
扇形的大小
180°
90°
以半圆为弧的扇形的圆心角是多少度?
以 圆为弧的扇形呢?
4
1
以半圆为弧的扇形的圆心角是180°。
360°× =90°
4
1
360°× =180°
2
1
?度
?度
圆心角度数
弧长与圆心角的关系
以半圆为弧的扇形的圆心角是周角的一半,
以 圆为弧的扇形圆心角是周角的 。
弧长占圆周长的几分之几,圆心角就占周角的几分之几。
1
4
1
4
1
4
选择正确的答案。
三个圆心角相等的扇形,( )的面积最大。
A.半径4厘米 B.半径3厘米 C.直径5厘米
A
练习二
分析:圆心角相等的扇形,半径越长,扇形面积越大。这里三个答案中,半径4厘米是最长的,所以选择A。
判断下列说法是否正确。对的打“√”,错的打“×”。
1、半径相等,圆心角越大,扇形的面积就越大。( )
2、圆的面积一定比扇形的面积大。( )
3、半圆形也是一个扇形。( )
练习三
1、半径相等,圆心角越大,扇形的面积就越大。( )
分析:半径相等的扇形,圆心角越大,面积越大。以图为例,半径都是2厘米,蓝色扇形圆心角大于黄色扇形圆心角,蓝色扇形面积大于黄色扇形面积,所以这题是对的。
√
r=2cm
r=2cm
2、圆的面积一定比扇形的面积大。( )
分析:当半径相等或圆的半径大于扇形半径时,此陈述是对的。
×
分析:当圆的半径小于扇形半径时,扇形面积可能大于圆的面积,这种情况下,此陈述是错的。
扇形的面积由半径和圆心角决定。
3、半圆形也是一个扇形。( )
分析:半圆形是以半圆为弧的扇形,它的圆心角是180°。
√
.
判断下列说法是否正确。对的打“√”,错的打“×”。
1、半径相等,圆心角越大,扇形的面积就越大。( )
2、圆的面积一定比扇形的面积大。( )
3、半圆形也是一个扇形。( )
√
√
×
练习三
求扇形面积
r=2cm
想:
1.扇形的圆心角多少度?
2.半径是多少?
3.这样的圆的面积是多大?
4.扇形的面积占整个圆面积的几分之几?
求扇形的面积
方法:
1.先把它看成圆,求出圆的面积。
2.图中可知,扇形的圆心角是90°。
3.90°占周角360°的 ,用圆面积× 得扇形面积。
1
4
1
4
r=2cm
提醒:带π计算可以简便准确。
求扇形面积
求扇形的面积
①S圆=πr2
=π×2×2
=4π(平方厘米)
小结方法
求扇形面积的方法:
1.把扇形看成圆,先求出圆的面积。
2.圆心角是周角的几分之几,就把圆的面积乘几分之几。
扇 形
一条( )
两条( )
一个( )
课堂小结
弧
半径
半径
圆心角
O
弧
圆心角
半径
弧
扇形
圆心角
圆心角
半径
圆上两点之间的部分叫做( ) 。
一条弧和经过这条弧两端的两条半径所围成的图形叫做( )。
顶点在圆心的角叫做( )。
扇形的大小与它的 ( )和 ( ) 有关。
扇 形
课堂小结
课堂小结
弧长占圆周长的几分之几
扇形面积占圆面积的几分之几
圆心角占周角的几分之几
扇 形
1、书本76页第1题、第3题。
2、画两个半径相等,圆心角不相等的扇形A和扇形B,比较它们面积的大小。
3、画两个圆心角相等,半径不相等的扇形C和扇形D,比较它们面积的大小。
作业
六年级—人教版—数学—第五单元
扇形
答疑
1.甲乙两个扇形,甲扇形的圆心角是30°,乙扇形的圆心角是90°,乙扇形和甲扇形的面积比是( )。
A.3∶1 B.1∶3 C.2:1 D.无法确定
D
分析:这道选择题考察我们的审题能力,扇形的大小既要考虑圆心角,也要考虑半径。有同学看到90°是30°的3倍,就选择A,那是忽略了还要看半径的长短。答案B和C可以排除,最后答案是D 。
答疑
2.半径不变,圆心角扩大到原来的3倍,扇形的面积扩大到 原来的( )倍。 A.2 B.3 C. 4 D.8
分析:这道题的解题依据是:在半径相等的圆里(即半径不变),圆心角越大,扇形的面积越大。圆心角扩大到原来的几倍,扇形的面积也扩大到原来的几倍。答案是B。
B
答疑
3.圆心角相等的扇形甲和乙,半径比是3∶2,面积比是( )。
A. 3∶2 B. 2∶3 C. 9∶4 D. 4∶9
C
答疑
分析:圆心角相等的扇形,半径越长,面积越大,可以排除B和D。扇形面积跟圆的面积有密切关系,半径比≠面积比,再排除A。半径比是3∶2,面积比是3的平方比2的平方,等于9∶4。用排除法和计算法都得到同一个结果,答案是C。
4.在一个半径是6厘米的圆里,画出一个圆心角是120°的扇形,求这个扇形面积列式是( ) ,结果是( )平方厘米。
37.68
π×6×6×
1
3
分析:这道题要从圆心角120°开始思考,120°是周角360°的三分之一,所以扇形面积是整个圆面积的三分之一,用圆的面积乘三分之一就行了。提醒大家,这里可以带π计算哦。
答疑
答疑到此结束
再见
六年级—人教版—数学—第五单元
扇形
1.知道扇形是从圆中产生,知道扇形各部分的名称(弧、半径、圆心角),会判断扇形及其圆心角。 2.通过回忆生活中扇形物品,抽象扇形的数学概念,掌握研究问题的一般方法 。 3.积累数学活动经验。
学习目标
生活中的扇形
生活中的扇形
A
B
弧
图上A、B两点之间的部分叫做弧。
读作“弧AB”。
扇形的组成
O
A
B
请读出绿色和蓝色这两条弧。
读作“弧CD”
读作“弧AB”
扇形的组成
C
D
A
B
O
半径
半径
弧
像∠ AOB这样,顶点在圆心的角叫做圆心角。
扇形的组成
下面各图中,哪些角是圆心角?(书:76页第2题)
√
√
练习一
圆心角的类别
圆心角可能是什么角?
锐角
钝角
平角
直角
270°
周角
圆心角的类别
圆心角可能是什么角?
锐角
钝角
直角
平角
周角
圆心角从锐角到周角都有可能。
A
B
O
半径
半径
弧
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
扇形的定义
半径
半径
弧
圆心角
O
扇形的组成
一条弧
两条半径 扇形
一个圆心角
扇形来自于一个与它圆心共用、半径相等的圆。
在同一个圆里,扇形的大小与什么有关系呢?
在同一个圆里,扇形的大小与圆心角有关。
1
3
4
在同圆里,圆心角越大,扇形就越大,圆心角越小,扇形就越小。
扇形的大小
60°
90°
30°
180°
1
2
.
在同一个圆里,扇形的大小与什么有关系呢?
3
扇形的大小
60°
90°
30°
180°
1
2
在同圆里,圆心角扩大到原来的几倍,扇形面积也扩大到原来的几倍。
4
r=2cm
r=3cm
猜猜下面两个扇形的面积,谁大谁小?
扇形的大小
.
.
r=2cm
r=3cm
圆心角相等,半径越长(短),
扇形面积越大(小)。
扇形的大小
.
.
影响扇形大小的条件有两个:一是圆心角的大小,二是半径的长短。
观察下面的扇形,想想它们的大小与什么有关?
扇形的大小
180°
90°
以半圆为弧的扇形的圆心角是多少度?
以 圆为弧的扇形呢?
4
1
以半圆为弧的扇形的圆心角是180°。
360°× =90°
4
1
360°× =180°
2
1
?度
?度
圆心角度数
弧长与圆心角的关系
以半圆为弧的扇形的圆心角是周角的一半,
以 圆为弧的扇形圆心角是周角的 。
弧长占圆周长的几分之几,圆心角就占周角的几分之几。
1
4
1
4
1
4
选择正确的答案。
三个圆心角相等的扇形,( )的面积最大。
A.半径4厘米 B.半径3厘米 C.直径5厘米
A
练习二
分析:圆心角相等的扇形,半径越长,扇形面积越大。这里三个答案中,半径4厘米是最长的,所以选择A。
判断下列说法是否正确。对的打“√”,错的打“×”。
1、半径相等,圆心角越大,扇形的面积就越大。( )
2、圆的面积一定比扇形的面积大。( )
3、半圆形也是一个扇形。( )
练习三
1、半径相等,圆心角越大,扇形的面积就越大。( )
分析:半径相等的扇形,圆心角越大,面积越大。以图为例,半径都是2厘米,蓝色扇形圆心角大于黄色扇形圆心角,蓝色扇形面积大于黄色扇形面积,所以这题是对的。
√
r=2cm
r=2cm
2、圆的面积一定比扇形的面积大。( )
分析:当半径相等或圆的半径大于扇形半径时,此陈述是对的。
×
分析:当圆的半径小于扇形半径时,扇形面积可能大于圆的面积,这种情况下,此陈述是错的。
扇形的面积由半径和圆心角决定。
3、半圆形也是一个扇形。( )
分析:半圆形是以半圆为弧的扇形,它的圆心角是180°。
√
.
判断下列说法是否正确。对的打“√”,错的打“×”。
1、半径相等,圆心角越大,扇形的面积就越大。( )
2、圆的面积一定比扇形的面积大。( )
3、半圆形也是一个扇形。( )
√
√
×
练习三
求扇形面积
r=2cm
想:
1.扇形的圆心角多少度?
2.半径是多少?
3.这样的圆的面积是多大?
4.扇形的面积占整个圆面积的几分之几?
求扇形的面积
方法:
1.先把它看成圆,求出圆的面积。
2.图中可知,扇形的圆心角是90°。
3.90°占周角360°的 ,用圆面积× 得扇形面积。
1
4
1
4
r=2cm
提醒:带π计算可以简便准确。
求扇形面积
求扇形的面积
①S圆=πr2
=π×2×2
=4π(平方厘米)
小结方法
求扇形面积的方法:
1.把扇形看成圆,先求出圆的面积。
2.圆心角是周角的几分之几,就把圆的面积乘几分之几。
扇 形
一条( )
两条( )
一个( )
课堂小结
弧
半径
半径
圆心角
O
弧
圆心角
半径
弧
扇形
圆心角
圆心角
半径
圆上两点之间的部分叫做( ) 。
一条弧和经过这条弧两端的两条半径所围成的图形叫做( )。
顶点在圆心的角叫做( )。
扇形的大小与它的 ( )和 ( ) 有关。
扇 形
课堂小结
课堂小结
弧长占圆周长的几分之几
扇形面积占圆面积的几分之几
圆心角占周角的几分之几
扇 形
1、书本76页第1题、第3题。
2、画两个半径相等,圆心角不相等的扇形A和扇形B,比较它们面积的大小。
3、画两个圆心角相等,半径不相等的扇形C和扇形D,比较它们面积的大小。
作业
六年级—人教版—数学—第五单元
扇形
答疑
1.甲乙两个扇形,甲扇形的圆心角是30°,乙扇形的圆心角是90°,乙扇形和甲扇形的面积比是( )。
A.3∶1 B.1∶3 C.2:1 D.无法确定
D
分析:这道选择题考察我们的审题能力,扇形的大小既要考虑圆心角,也要考虑半径。有同学看到90°是30°的3倍,就选择A,那是忽略了还要看半径的长短。答案B和C可以排除,最后答案是D 。
答疑
2.半径不变,圆心角扩大到原来的3倍,扇形的面积扩大到 原来的( )倍。 A.2 B.3 C. 4 D.8
分析:这道题的解题依据是:在半径相等的圆里(即半径不变),圆心角越大,扇形的面积越大。圆心角扩大到原来的几倍,扇形的面积也扩大到原来的几倍。答案是B。
B
答疑
3.圆心角相等的扇形甲和乙,半径比是3∶2,面积比是( )。
A. 3∶2 B. 2∶3 C. 9∶4 D. 4∶9
C
答疑
分析:圆心角相等的扇形,半径越长,面积越大,可以排除B和D。扇形面积跟圆的面积有密切关系,半径比≠面积比,再排除A。半径比是3∶2,面积比是3的平方比2的平方,等于9∶4。用排除法和计算法都得到同一个结果,答案是C。
4.在一个半径是6厘米的圆里,画出一个圆心角是120°的扇形,求这个扇形面积列式是( ) ,结果是( )平方厘米。
37.68
π×6×6×
1
3
分析:这道题要从圆心角120°开始思考,120°是周角360°的三分之一,所以扇形面积是整个圆面积的三分之一,用圆的面积乘三分之一就行了。提醒大家,这里可以带π计算哦。
答疑
答疑到此结束
再见
