2022—2023学年苏科版数学八年级上册 2.2 轴对称的性质 课件 (共24张PPT)
文档属性
| 名称 | 2022—2023学年苏科版数学八年级上册 2.2 轴对称的性质 课件 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 397.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 19:11:24 | ||
图片预览




文档简介
(共24张PPT)
苏科版 八年级上册数学
第2章 轴对称与轴对称图形
2.2 轴对称的性质(1)
你能结合具体的图形说明轴对称图形和两个图形成轴对称有什么联系与区别吗?
两者的联系:
①把成轴对称的两个图形看成一个整体,它就是
一个轴对称图形.
②把一个轴对称图形沿对称轴分成两个图形,这
两个图形关于这条轴对称.
知识回顾
两者的区别:
轴对称图形指的是一个图形沿对称轴折叠后这个图形的两部分能完全重合,而两个图形成轴对称指的是两个图形之间的位置关系,这两个图形沿对称轴折叠后能够重合.
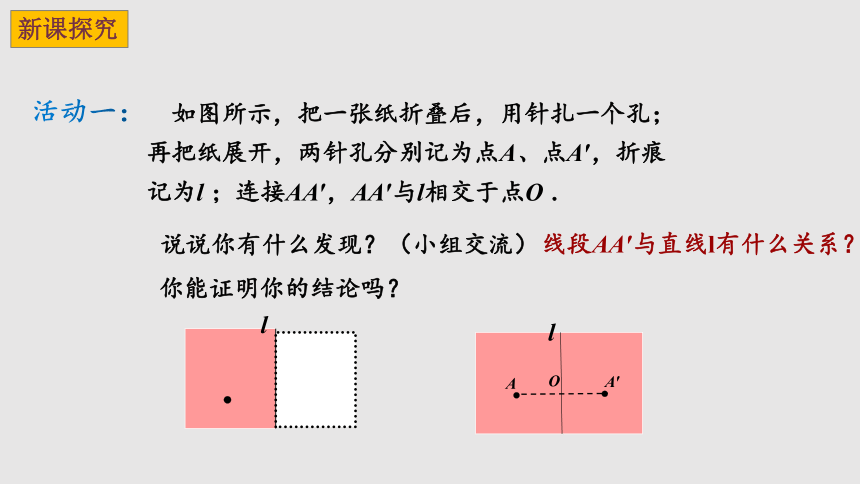
如图所示,把一张纸折叠后,用针扎一个孔;再把纸展开,两针孔分别记为点A、点A′,折痕记为l ;连接AA′,AA′与l相交于点O .
说说你有什么发现?(小组交流)
活动一:
A
●
l
●
A′
O
l
●
线段AA′与直线l有什么关系?
你能证明你的结论吗?
新课探究
∴ 线段OA、OA′重合,
∵ ∠1=∠2 且 ∠1+∠2=180°,
即 O是AA′的中点.
∴ ∠1=∠2=90°.
l
A
A′
●
●
2
o
1
∴ 直线l 垂直且平分AA′.
∵ 把纸沿折痕 l 折叠时,点A、A′重合,
新课探究
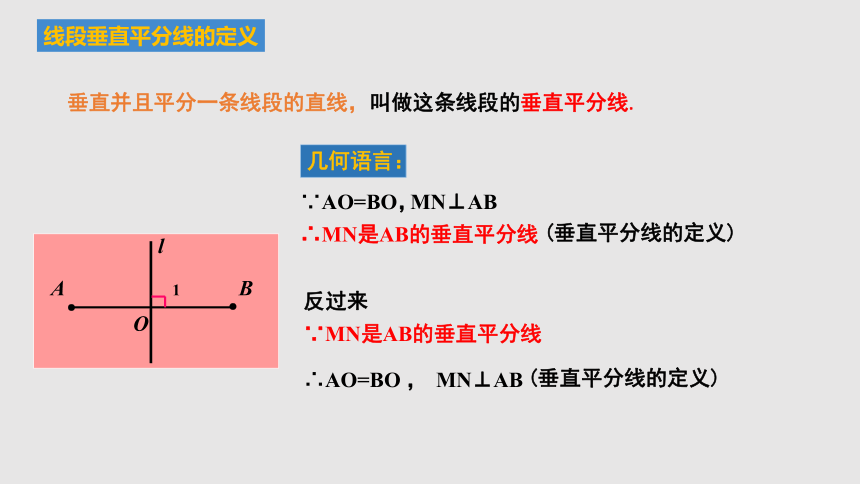
垂直并且平分一条线段的直线,叫做这条线段的垂直平分线.
几何语言:
∴MN是AB的垂直平分线
MN⊥AB
∵AO=BO,
∵MN是AB的垂直平分线
MN⊥AB
∴AO=BO ,
(垂直平分线的定义)
(垂直平分线的定义)
反过来
线段垂直平分线的定义
B
A
●
●
1
O
l
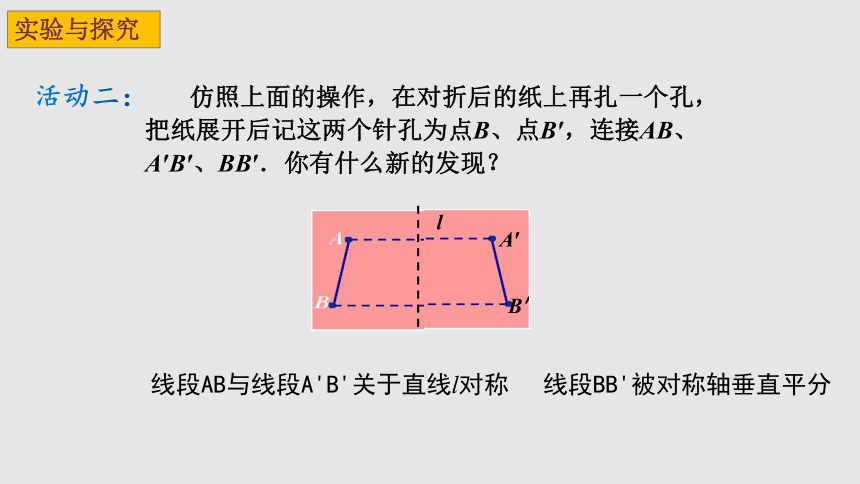
仿照上面的操作,在对折后的纸上再扎一个孔,把纸展开后记这两个针孔为点B、点B′,连接AB、A′B′、BB′.你有什么新的发现?
A′
B′
l
活动二:
线段AB与线段A'B'关于直线l对称
线段BB'被对称轴垂直平分
实验与探究
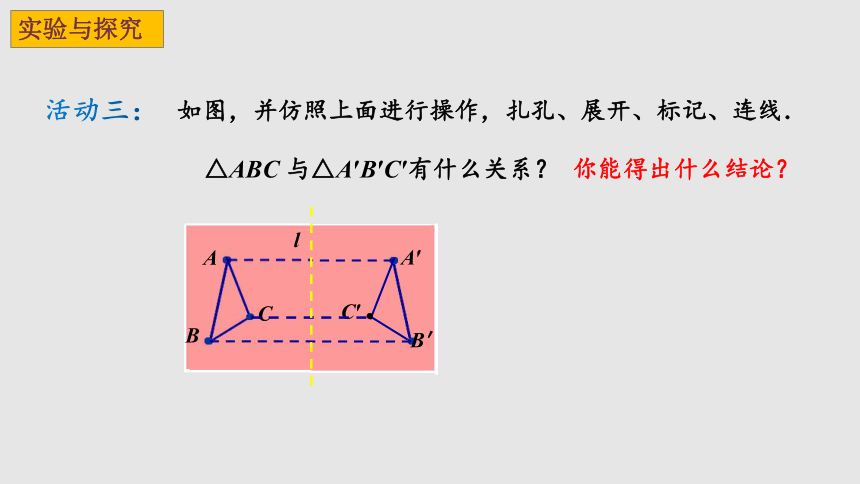
如图,并仿照上面进行操作,扎孔、展开、标记、连线.
△ABC 与△A′B′C′有什么关系?
你能得出什么结论?
A
C
B
A′
B′
●
C′
l
活动三:
实验与探究
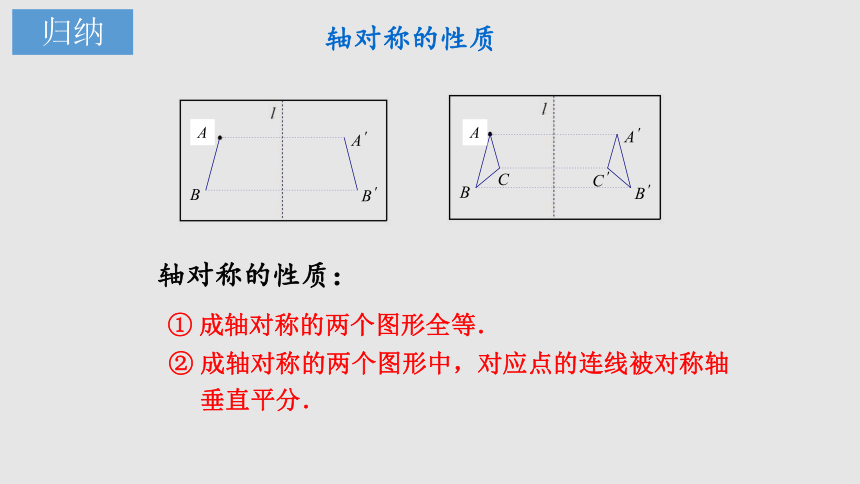
① 成轴对称的两个图形全等.
② 成轴对称的两个图形中,对应点的连线被对称轴
垂直平分.
轴对称的性质:
轴对称的性质
A
A
归纳
二、轴对称图形对称轴的画法
画出下列图形的对称轴.
如果没有方格子,而又不能折叠,你还能比较准确的画出图形的对称轴吗?
试一试
做一做
1.画出下面图形的对称轴,画完图后请思考下面的问题:
①能总结你画对称轴的方法吗?
②连结对称点的线段与对称轴有什么关系?
连结对称点的线段被对称轴垂直平分
2.如图,点A和点A 关于某条直线成轴对称,你能画出这条直线吗?
A . . A
总结归纳
(1)找出图形的任意一组对称点
画图形的对称轴的画法
(2)连结对称点
(3)画出对称点所连线段的垂直平分线,就可以得到该图形的对称轴。
结论:如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
1.已知对称轴 l 和一个点A,如何画出点A关于l 的对应点A′
所以点A′就是点A关于l的对称点.
A
A′
作法:
1.过点A作对称轴l的垂线,垂足为B;
2.延长AB 至A′,使得BA′=AB.
B
l
【做一做】
1.如何画线段AB关于直线 l 的对称线段A′B′
找关键点作出其对称点,
然后连接线段.
A
B
A′
B′
【练一练】
B′
A′
2.如何画 △ABC关于直线 l 对称的△ A′B′C′
找关键点作出其对称点,
然后首尾顺次连接线段构成三角形.
A
B
C
C′
课堂练习
1.如图,若△ABC 与△A′B′C′关于直线 MN 对称,BB′交 MN 于点 O,则下列说法不一定正确的是( )
A.AC=A′C′ B.BO=B′O
C.AA′⊥MN D.AB∥B′C′
D
2.如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为( )
B
A.48° B.54°
C.74° D.78°
3.下列说法中正确的是( )
A.两个全等三角形,一定是轴对称的
B.两个轴对称的三角形,一定全等
C.三角形的一条中线把三角形分成以中线为轴对称的两个图形
D.三角形的一条高把三角形分成以高线为轴对称的两个图形
B
4. 如图,△ABC与△DEF关于直线MN对称,则以
下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被MN垂直平分
A
5.把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )
A.
B.
C.
D.
C
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD,若A到河岸CD的中点的距离为500m,若牧童从A处将牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?最短路程是多少?
A
D
C
B
N
M
A′
1000m
拓展延伸
变:如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC≠BD,若牧童从A处将牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?
A
D
C
B
M
A′
课堂小结
通过这节课的学习,你有什么收获
知识:
方法:
思想:
沿直线对
折重合
轴对称图形
任何一对对应点所连线段的垂直平分线
对称轴
轴对称
课堂小结
苏科版 八年级上册数学
第2章 轴对称与轴对称图形
2.2 轴对称的性质(1)
你能结合具体的图形说明轴对称图形和两个图形成轴对称有什么联系与区别吗?
两者的联系:
①把成轴对称的两个图形看成一个整体,它就是
一个轴对称图形.
②把一个轴对称图形沿对称轴分成两个图形,这
两个图形关于这条轴对称.
知识回顾
两者的区别:
轴对称图形指的是一个图形沿对称轴折叠后这个图形的两部分能完全重合,而两个图形成轴对称指的是两个图形之间的位置关系,这两个图形沿对称轴折叠后能够重合.
如图所示,把一张纸折叠后,用针扎一个孔;再把纸展开,两针孔分别记为点A、点A′,折痕记为l ;连接AA′,AA′与l相交于点O .
说说你有什么发现?(小组交流)
活动一:
A
●
l
●
A′
O
l
●
线段AA′与直线l有什么关系?
你能证明你的结论吗?
新课探究
∴ 线段OA、OA′重合,
∵ ∠1=∠2 且 ∠1+∠2=180°,
即 O是AA′的中点.
∴ ∠1=∠2=90°.
l
A
A′
●
●
2
o
1
∴ 直线l 垂直且平分AA′.
∵ 把纸沿折痕 l 折叠时,点A、A′重合,
新课探究
垂直并且平分一条线段的直线,叫做这条线段的垂直平分线.
几何语言:
∴MN是AB的垂直平分线
MN⊥AB
∵AO=BO,
∵MN是AB的垂直平分线
MN⊥AB
∴AO=BO ,
(垂直平分线的定义)
(垂直平分线的定义)
反过来
线段垂直平分线的定义
B
A
●
●
1
O
l
仿照上面的操作,在对折后的纸上再扎一个孔,把纸展开后记这两个针孔为点B、点B′,连接AB、A′B′、BB′.你有什么新的发现?
A′
B′
l
活动二:
线段AB与线段A'B'关于直线l对称
线段BB'被对称轴垂直平分
实验与探究
如图,并仿照上面进行操作,扎孔、展开、标记、连线.
△ABC 与△A′B′C′有什么关系?
你能得出什么结论?
A
C
B
A′
B′
●
C′
l
活动三:
实验与探究
① 成轴对称的两个图形全等.
② 成轴对称的两个图形中,对应点的连线被对称轴
垂直平分.
轴对称的性质:
轴对称的性质
A
A
归纳
二、轴对称图形对称轴的画法
画出下列图形的对称轴.
如果没有方格子,而又不能折叠,你还能比较准确的画出图形的对称轴吗?
试一试
做一做
1.画出下面图形的对称轴,画完图后请思考下面的问题:
①能总结你画对称轴的方法吗?
②连结对称点的线段与对称轴有什么关系?
连结对称点的线段被对称轴垂直平分
2.如图,点A和点A 关于某条直线成轴对称,你能画出这条直线吗?
A . . A
总结归纳
(1)找出图形的任意一组对称点
画图形的对称轴的画法
(2)连结对称点
(3)画出对称点所连线段的垂直平分线,就可以得到该图形的对称轴。
结论:如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
1.已知对称轴 l 和一个点A,如何画出点A关于l 的对应点A′
所以点A′就是点A关于l的对称点.
A
A′
作法:
1.过点A作对称轴l的垂线,垂足为B;
2.延长AB 至A′,使得BA′=AB.
B
l
【做一做】
1.如何画线段AB关于直线 l 的对称线段A′B′
找关键点作出其对称点,
然后连接线段.
A
B
A′
B′
【练一练】
B′
A′
2.如何画 △ABC关于直线 l 对称的△ A′B′C′
找关键点作出其对称点,
然后首尾顺次连接线段构成三角形.
A
B
C
C′
课堂练习
1.如图,若△ABC 与△A′B′C′关于直线 MN 对称,BB′交 MN 于点 O,则下列说法不一定正确的是( )
A.AC=A′C′ B.BO=B′O
C.AA′⊥MN D.AB∥B′C′
D
2.如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为( )
B
A.48° B.54°
C.74° D.78°
3.下列说法中正确的是( )
A.两个全等三角形,一定是轴对称的
B.两个轴对称的三角形,一定全等
C.三角形的一条中线把三角形分成以中线为轴对称的两个图形
D.三角形的一条高把三角形分成以高线为轴对称的两个图形
B
4. 如图,△ABC与△DEF关于直线MN对称,则以
下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被MN垂直平分
A
5.把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )
A.
B.
C.
D.
C
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD,若A到河岸CD的中点的距离为500m,若牧童从A处将牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?最短路程是多少?
A
D
C
B
N
M
A′
1000m
拓展延伸
变:如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC≠BD,若牧童从A处将牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?
A
D
C
B
M
A′
课堂小结
通过这节课的学习,你有什么收获
知识:
方法:
思想:
沿直线对
折重合
轴对称图形
任何一对对应点所连线段的垂直平分线
对称轴
轴对称
课堂小结
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
