华东师大版八年级数学上册 14.1.1 直角三角形三边关系 导学案(无答案)
文档属性
| 名称 | 华东师大版八年级数学上册 14.1.1 直角三角形三边关系 导学案(无答案) | 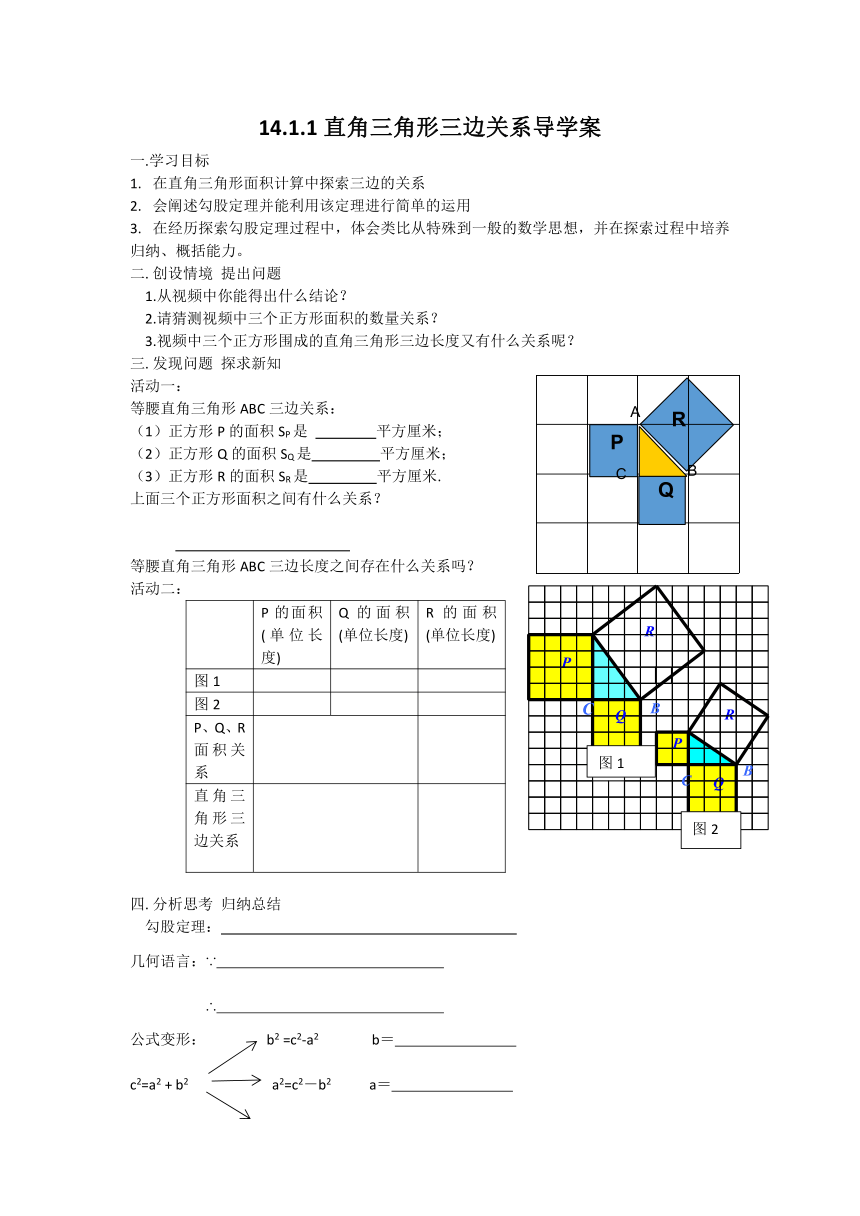 | |
| 格式 | docx | ||
| 文件大小 | 162.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 15:51:04 | ||
图片预览

文档简介
14.1.1直角三角形三边关系导学案
一.学习目标
在直角三角形面积计算中探索三边的关系
会阐述勾股定理并能利用该定理进行简单的运用
在经历探索勾股定理过程中,体会类比从特殊到一般的数学思想,并在探索过程中培养归纳、概括能力。
创设情境 提出问题
1.从视频中你能得出什么结论?
2.请猜测视频中三个正方形面积的数量关系?
3.视频中三个正方形围成的直角三角形三边长度又有什么关系呢?
发现问题 探求新知
活动一:
等腰直角三角形ABC三边关系:
正方形P的面积SP是 平方厘米;
正方形Q的面积SQ是 平方厘米;
正方形R的面积SR是 平方厘米.
上面三个正方形面积之间有什么关系?
等腰直角三角形ABC三边长度之间存在什么关系吗?
活动二:
P的面积(单位长度) Q的面积(单位长度) R的面积(单位长度)
图1
图2
P、Q、R面积关系
直角三角形三边关系
分析思考 归纳总结
勾股定理:
几何语言:∵
∴
公式变形: b2 =c2-a2 b=
c2=a2 + b2 a2=c2-b2 a=
强化训练 巩固双基 A
例 在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a; C B
例 用四个全等的直角三角形,还可以拼成如图所示的图形,你能否根据这一图形,证明勾股定理.
大正方形的面积可以表示为 ;
也可以表示为 .
∵
∴
课堂小结
本节课你学到了什么?
七.课后作业
1.求图中直角三角形中未知线段的长度:b=_____,c=_____.
3.如图所示为一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作两个正方形②,…,以此类推,若正方形①的面积为64,则一个正方形⑤的面积为____.
一.学习目标
在直角三角形面积计算中探索三边的关系
会阐述勾股定理并能利用该定理进行简单的运用
在经历探索勾股定理过程中,体会类比从特殊到一般的数学思想,并在探索过程中培养归纳、概括能力。
创设情境 提出问题
1.从视频中你能得出什么结论?
2.请猜测视频中三个正方形面积的数量关系?
3.视频中三个正方形围成的直角三角形三边长度又有什么关系呢?
发现问题 探求新知
活动一:
等腰直角三角形ABC三边关系:
正方形P的面积SP是 平方厘米;
正方形Q的面积SQ是 平方厘米;
正方形R的面积SR是 平方厘米.
上面三个正方形面积之间有什么关系?
等腰直角三角形ABC三边长度之间存在什么关系吗?
活动二:
P的面积(单位长度) Q的面积(单位长度) R的面积(单位长度)
图1
图2
P、Q、R面积关系
直角三角形三边关系
分析思考 归纳总结
勾股定理:
几何语言:∵
∴
公式变形: b2 =c2-a2 b=
c2=a2 + b2 a2=c2-b2 a=
强化训练 巩固双基 A
例 在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a; C B
例 用四个全等的直角三角形,还可以拼成如图所示的图形,你能否根据这一图形,证明勾股定理.
大正方形的面积可以表示为 ;
也可以表示为 .
∵
∴
课堂小结
本节课你学到了什么?
七.课后作业
1.求图中直角三角形中未知线段的长度:b=_____,c=_____.
3.如图所示为一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作两个正方形②,…,以此类推,若正方形①的面积为64,则一个正方形⑤的面积为____.
