人教版八年级上册数学 11.2.1 三角形的内角 拓展练习(word版含解析)
文档属性
| 名称 | 人教版八年级上册数学 11.2.1 三角形的内角 拓展练习(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 336.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 00:00:00 | ||
图片预览




文档简介
《三角形的内角》拓展练习
一、选择题。
1.已知△ABC,
(1)如图1,若A1点是∠ABC和∠ACD的角平分线的交点,则∠A1=∠A;
(2)如图2,若F点是∠ABC和∠DCE的角平分线的交点,则∠F=(∠A+∠D)﹣90°;
(3)如图3,若A1点是∠ABC和∠ACD的角平分线的交点,E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,则∠Q﹣∠A1=90°.
上述说法正确的个数是( )
A.0个 B.1个 C.2个 D.3个
2.在△ABC中,如果∠A﹣∠B=90°,那么△ABC是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.以上三种都可能
3.如图,将一副三角板按如图方式叠放,则角α等于( )
A.165° B.135° C.105° D.75°
4.如图,在△ABC中,∠C=78°,沿图中虚线截去∠C,则∠1+∠2=( )
A.282° B.180° C.360° D.258°
5.等腰三角形的一个内角是100°,它的另外两个角的度数是( )
A.50° 和 50° B.40° 和 40° C.35° 和 35° D.60° 和20°
二、填空题。
6.如图,在三角形ABC中,AD⊥BC,垂足为点D,直线EF过点C,且90°﹣∠FCB=∠BAD,点G为线段AB上一点,连接CG,∠BCG与∠BCE的角平分线CM、CN分别交AD于点M、N,若∠BGC=70°,则∠MCN= °.
7.已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC= .(用α,β表示)
8.在△ABC中,∠A=36°,当∠C= ,△ABC为等腰三角形.
9.如图1,在△ABC中,∠ABC,∠ACB的角平分线交于点O,则∠BOC=90°+∠A=×180°+∠A.如图2,在△ABC中,∠ABC,∠ACB的两条三等分角线分别对应交于O1,O2,则∠BO1C=×180°+∠A,∠BO2C=×180°+∠A.根据以上阅读理解,你能猜想∠BO2018C= .
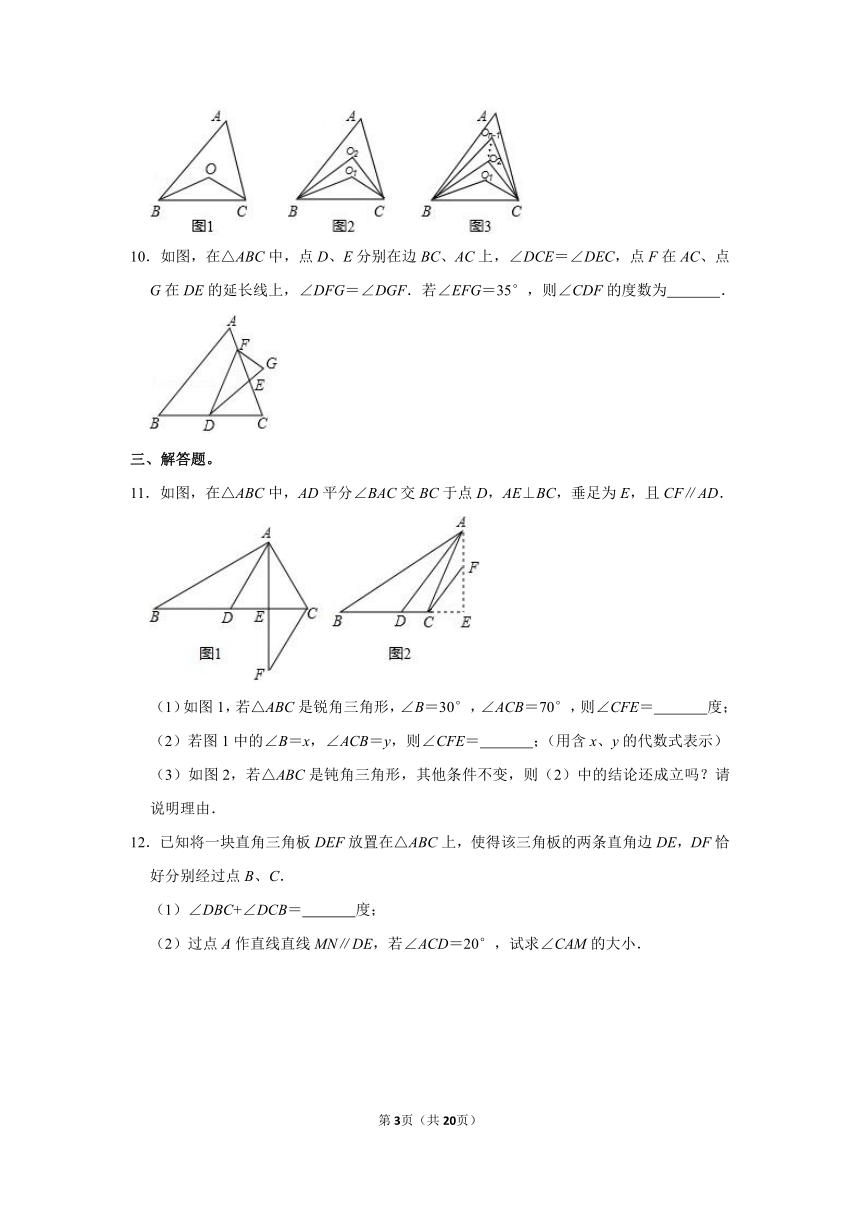
10.如图,在△ABC中,点D、E分别在边BC、AC上,∠DCE=∠DEC,点F在AC、点G在DE的延长线上,∠DFG=∠DGF.若∠EFG=35°,则∠CDF的度数为 .
三、解答题。
11.如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.
(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE= 度;
(2)若图1中的∠B=x,∠ACB=y,则∠CFE= ;(用含x、y的代数式表示)
(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.
12.已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,DF恰好分别经过点B、C.
(1)∠DBC+∠DCB= 度;
(2)过点A作直线直线MN∥DE,若∠ACD=20°,试求∠CAM的大小.
13.如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠DAE、∠BOA的度数.
14.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=42°.
(1)求∠BOC的度数;
(2)把(1)中∠A=42°这个条件去掉,试探索∠BOC和∠A之间有怎样的数量关系.
15.探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
《三角形的内角》拓展练习
参考答案与试题解析
一、选择题。
1.已知△ABC,
(1)如图1,若A1点是∠ABC和∠ACD的角平分线的交点,则∠A1=∠A;
(2)如图2,若F点是∠ABC和∠DCE的角平分线的交点,则∠F=(∠A+∠D)﹣90°;
(3)如图3,若A1点是∠ABC和∠ACD的角平分线的交点,E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,则∠Q﹣∠A1=90°.
上述说法正确的个数是( )
A.0个 B.1个 C.2个 D.3个
【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,根据角平分线的定义可得∠A1CD=∠ACD,∠A1BC=∠ABC,然后整理即可得到∠A1=∠A;
(2)①根据四边形的内角和定理表示出∠BCD,再表示出∠DCE,然后根据角平分线的定义可得∠FBC=∠ABC,∠FCE=∠DCE,三角形的一个外角等于与它不相邻的两个内角的和可得∠F+∠FBC=∠FCE,然后整理即可得解;
(3)根据三角形的内角和定理表示出∠ACE+∠AEC,再根据角平分线的定义表示出∠QCE+∠QEC,然后利用三角形的内角和定理列式整理即可得解.
【解答】解:(1)由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∵∠ABC的角平分线与∠ACB的外角平分线交于A1,
∴∠A1CD=∠ACD,∠A1BC=∠ABC,
∴∠A1+∠A1BC=(∠A+∠ABC)=∠A+∠ABC,
∴∠A1=∠A;
(2)由四边形内角和定理得,∠BCD=360°﹣∠A﹣∠D﹣∠ABC,
∴∠DCE=180°﹣(360°﹣∠A﹣∠D﹣∠ABC)=∠A+∠D+∠ABC﹣180°,
由三角形的外角性质得,∠FCE=∠F+∠FBC,
∵BF、CF分别是∠ABC和∠DCE的平分线,
∴∠FBC=∠ABC,∠FCE=∠DCE,
∴∠F+∠FBC=(∠A+∠D+∠ABC﹣180°)=(∠A+∠D)+∠ABC﹣90°,
∴∠F=(∠A+∠D)﹣90°,
(3)∵EQ、CQ分别为∠AEC、∠ACE的角平分线,
∴∠QEC=∠AEC,∠QCE=∠ACE,
又∵∠AEC+∠ACE=∠BAC,
∴∠Q=180°﹣(∠QEC+∠QCE)=180°﹣(∠AEC+∠ACE),
=180°﹣∠BAC,
由(1)可知∠BAC=2∠A1,
∴∠Q=180°﹣∠A1,
∴∠Q+∠A1=180°.
故(1)(2)正确;
故选:C.
【点评】本题考查了三角形的内角和定理,角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键,要注意整体思想的利用.
2.在△ABC中,如果∠A﹣∠B=90°,那么△ABC是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.以上三种都可能
【分析】根据三角形内角和定理以及三角形的分类可知.
【解答】解:∵∠A﹣∠B=90°,
∴∠A=90°+∠B,
∴∠A大于90°.
根据三角形性质可知大于90°的角为钝角,
∴此三角形为钝角三角形.
故选:B.
【点评】本题考查的是三角形内角和定理,熟练掌握三角形的内角和是解题的关键.
3.如图,将一副三角板按如图方式叠放,则角α等于( )
A.165° B.135° C.105° D.75°
【分析】根据三角形内角和定理求出∠1,根据三角形外角的性质求出∠2,根据邻补角的概念计算即可.
【解答】解:∠1=90°﹣30°﹣60°,
∴∠2=∠1﹣45°=15°,
∴∠α=180°﹣15°=165°,
故选:A.
【点评】本题考查的是三角形内角和定理和三角形的外角的性质,掌握三角形内角和等于180°是解题的关键.
4.如图,在△ABC中,∠C=78°,沿图中虚线截去∠C,则∠1+∠2=( )
A.282° B.180° C.360° D.258°
【分析】根据三角形内角和定理求出∠3+∠4,根据邻补角的概念计算即可.
【解答】解:∵∠C=78°,
∴∠3+∠4=180°﹣78°=102°,
∴∠1+∠2=360°﹣(∠3+∠4)=258°,
故选:D.
【点评】本题考查的是三角形内角和定理,掌握三角形内角和等于180°是解题的关键.
5.等腰三角形的一个内角是100°,它的另外两个角的度数是( )
A.50° 和 50° B.40° 和 40° C.35° 和 35° D.60° 和20°
【分析】先判断出100°的角是顶角,再根据等腰三角形的两底角相等解答.
【解答】解:∵等腰三角形的一个角100°,
∴100°的角是顶角,
∴另两个底角都是(180°﹣100°)=40°,
故选:B.
【点评】本题考查了等腰三角形的性质,主要利用了等腰三角形两底角相等,需要注意100°的角不可能是底角.
二、填空题。
6.如图,在三角形ABC中,AD⊥BC,垂足为点D,直线EF过点C,且90°﹣∠FCB=∠BAD,点G为线段AB上一点,连接CG,∠BCG与∠BCE的角平分线CM、CN分别交AD于点M、N,若∠BGC=70°,则∠MCN= 35 °.
【分析】依据90°﹣∠B=∠BAD,90°﹣∠FCB=∠BAD,可得∠FCB=∠B,进而判定EF∥AB,即可得到∠ECG=∠BGC=70°,再根据∠MCN=∠BCN﹣∠BCM=(∠BCE﹣∠BCG)=∠ECG,即可得到结论.
【解答】解:∵AD⊥BC,
∴Rt△ABD中,90°﹣∠B=∠BAD,
又∵90°﹣∠FCB=∠BAD,
∴∠FCB=∠B,
∴EF∥AB,
∴∠ECG=∠BGC=70°,
∵∠BCG与∠BCE的角平分线CM、CN分别交AD于点M、N,
∴∠BCN=∠BCE,∠BCM=∠BCG,
∴∠MCN=∠BCN﹣∠BCM=(∠BCE﹣∠BCG)=∠ECG=×70°=35°,
故答案为:35.
【点评】本题考查了平行线的性质和判定以及角平分线的定义的综合运用,解题时注意平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.
7.已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC= (α+β) .(用α,β表示)
【分析】连接BC,根据角平分线的性质得到∠3=ABP,∠4=ACP,根据三角形的内角和得到∠1+∠2=180°﹣β,2(∠3+∠4)+(∠1+∠2)=180°﹣α,求出∠3+∠4=(β﹣α),根据三角形的内角和即可得到结论.
【解答】解:连接BC,
∵BQ平分∠ABP,CQ平分∠ACP,
∴∠3=ABP,∠4=ACP,
∵∠1+∠2=180°﹣β,2(∠3+∠4)+(∠1+∠2)=180°﹣α,
∴∠3+∠4=(β﹣α),
∵∠BQC=180°﹣(∠1+∠2)﹣(∠3+∠4)=180°﹣(180°﹣β)﹣(β﹣α),
即:∠BQC=(α+β).
故答案为:(α+β).
【点评】本题考查了三角形的内角和,角平分线的定义,连接BC构造三角形是解题的关键.
8.在△ABC中,∠A=36°,当∠C= 72°,36°,108° ,△ABC为等腰三角形.
【分析】分三种情形分别讨论,运用三角形内角和定理即可解决问题
【解答】解:①当AB=AC时,
∵∠A=36°,
∴∠C=∠B=72°.
②当CA=CB时,
∵∠A=∠B=36°,
∴∠C=108°.
③当BA=BC时,
∴∠C=∠A=36°,
综上所述,∠C的值为72°或108°或36°,
故答案为:72°,36°,108°.
【点评】本题考查等腰三角形的判定和性质以及三角形内角和定理的运用,解题的关键是用分类讨论的思想思考问题.
9.如图1,在△ABC中,∠ABC,∠ACB的角平分线交于点O,则∠BOC=90°+∠A=×180°+∠A.如图2,在△ABC中,∠ABC,∠ACB的两条三等分角线分别对应交于O1,O2,则∠BO1C=×180°+∠A,∠BO2C=×180°+∠A.根据以上阅读理解,你能猜想∠BO2018C= +∠A .
【分析】根据已知中的特例,观察两部分前边的倍数和n等分线间的关系,从而写出结论.
【解答】解:如图3,根据题中所给的信息,总结可得:
∠BO1C=×180°+∠A,
∠BOn﹣1C=×180°+∠A.
∴当n﹣1=2018时,n=2019,即∠BO2018C=+∠A.
故答案为:+∠A.
【点评】本题考查了三角形的内角和定理,综合运用了三角形的内角和定理和n等分角的概念,注意由特殊到一般的总结.
10.如图,在△ABC中,点D、E分别在边BC、AC上,∠DCE=∠DEC,点F在AC、点G在DE的延长线上,∠DFG=∠DGF.若∠EFG=35°,则∠CDF的度数为 70° .
【分析】根据三角形内角和定理求出x+y=145,在△FDC中,根据三角形内角和定理求出即可.
【解答】解:∵∠DCE=∠DEC,∠DFG=∠DGF,
∴设∠DCE=∠DEC=x°,∠DFG=∠DGF=y°,
则∠FEG=∠DEC=x°,
∵在△GFE中,∠EFG=35°,
∴∠FEG+∠DGF=x°+y°=180°﹣35°=145°,
即x+y=145,
在△FDC中,∠CDF=180°﹣∠DCE﹣∠DFC=180°﹣x°﹣(y°﹣35°)
=215°﹣(x°+y°)
=70°,
故答案为:70°.
【点评】本题考查了三角形内角和定理,能求出x+y=145是解此题的关键.
三、解答题。
11.如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.
(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE= 20 度;
(2)若图1中的∠B=x,∠ACB=y,则∠CFE= y﹣x ;(用含x、y的代数式表示)
(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.
【分析】(1)求∠CFE的度数,求出∠DAE的度数即可,只要求出∠BAE﹣∠BAD的度数,由平分和垂直易得∠BAE和∠BAD的度数即可;
(2)由(1)类推得出答案即可;
(3)类比以上思路,把问题转换为∠CFE=90°﹣∠ECF即可解决问题.
【解答】解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°﹣∠B﹣∠ACB=80°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵AE⊥BC,
∴∠AEB=90°
∴∠BAE=60°
∴∠DAE=∠BAE﹣∠BAD=60°﹣40°=20°,
∵CF∥AD,
∴∠CFE=∠DAE=20°;
故答案为:20;
(2)∵∠BAE=90°﹣∠B,∠BAD=∠BAC=(180°﹣∠B﹣∠BCA),
∴∠CFE=∠DAE=∠BAE﹣∠BAD=90°﹣∠B﹣(180°﹣∠B﹣∠BCA)=(∠BCA﹣∠B)=y﹣x.
故答案为:y﹣x;
(3)(2)中的结论成立.
∵∠B=x,∠ACB=y,
∴∠BAC=180°﹣x﹣y,
∵AD平分∠BAC,
∴∠DAC=∠BAC=90°﹣x﹣y,
∵CF∥AD,
∴∠ACF=∠DAC=90°﹣x﹣y,
∴∠BCF=y+90°﹣x﹣y=90°﹣x+y,
∴∠ECF=180°﹣∠BCF=90°+x﹣y,
∵AE⊥BC,
∴∠FEC=90°,
∴∠CFE=90°﹣∠ECF=y﹣x.
【点评】此题考查三角形的内角和定理,角平分线的性质,平行线的性质以及垂直的意义等知识,结合图形,灵活选择适当的方法解决问题.
12.已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,DF恰好分别经过点B、C.
(1)∠DBC+∠DCB= 90 度;
(2)过点A作直线直线MN∥DE,若∠ACD=20°,试求∠CAM的大小.
【分析】(1)在△DBC中,根据三角形内角和定理得∠DBC+∠DCB+∠D=180°,然后把∠D=90°代入计算即可;
(2)在Rt△ABC中,根据三角形内角和定理得∠ABC+∠ACB+∠A=180°,即,∴∠ABD+∠BAC=90°﹣∠ACD=70°,整体代入即可得出结论.
【解答】解:(1)在△DBC中,∵∠DBC+∠DCB+∠D=180°,
而∠D=90°,
∴∠DBC+∠DCB=90°;
故答案为90;
(2)在△ABC中,
∵∠ABC+∠ACB+∠A=180°,
即∠ABD+∠DBC+∠DCB+∠ACD+∠BAC=180°,
而∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=90°﹣∠BAC,
∴∠ABD+∠BAC=90°﹣∠ACD=70°.
又∵MN∥DE,
∴∠ABD=∠BAN.
而∠BAN+∠BAC+∠CAM=180°,
∴∠ABD+∠BAC+∠CAM=180°,
∴∠CAM=180°﹣(∠ABD+∠BAC)=110°.
【点评】此题主要考查了三角形内角和定理,平行线的性质,解本题的关键是求出∠ABD+∠BAC=70°.
13.如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠DAE、∠BOA的度数.
【分析】根据垂直的定义、角平分线的定义、三角形内角和定理计算即可.
【解答】解∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°﹣90°﹣70°=20°,
∵∠BAC=60°,AE是∠BAC的角平分线,
∴∠EAC=∠BAE=30°,
∴∠EAD=∠EAC﹣∠CAD=30°﹣20°=10°,
∠ABC=180°﹣∠BAC﹣∠C=50°,
∵BF是∠ABC的角平分线,
∴∠ABO=25°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣30°﹣25°=125°.
故∠DAE,∠BOA的度数分别是10°,125°.
【点评】本题考查的是三角形内角和定理、三角形的高和角平分线的定义,掌握三角形内角和等于180°是解题的关键.
14.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=42°.
(1)求∠BOC的度数;
(2)把(1)中∠A=42°这个条件去掉,试探索∠BOC和∠A之间有怎样的数量关系.
【分析】(1)先求出∠ABC+∠ACB的度数,根据平分线的定义得出∠1=∠ABC,∠2=∠ACB,求出∠1+∠2的度数,根据三角形内角和定理求出∠BOC即可;
(2)根据角平分线的定义可得∠1=∠ABC,∠2=∠ACB,然后用∠A表示出∠1+∠2,再根据三角形的内角和等于180°列式整理即可得出结论.
【解答】解:(1)∵∠A=42°,
∴∠ABC+∠ACB=180°﹣∠A=138°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠1=∠ABC,∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB)==69°,
∴∠BOC=180°﹣(∠1+∠2)=180°﹣69°=111°;
(2)∠BOC=90°+∠A,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠1=∠ABC,∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB)=(180°﹣∠A),
∴∠BOC=180°﹣(∠1+∠2)=180=90.
【点评】本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.
15.探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX= 50 °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
【分析】(1)首先连接AD并延长至点F,然后根据外角的性质,即可判断出∠BDC=∠A+∠B+∠C.
(2)①由(1)可得∠ABX+∠ACX+∠A=∠BXC,然后根据∠A=40°,∠BXC=90°,求出∠ABX+∠ACX的值是多少即可.
②由(1)可得∠DBE=∠DAE+∠ADB+∠AEB,再根据∠DAE=40°,∠DBE=130°,求出∠ADB+∠AEB的值是多少;然后根据∠DCE=(∠ADB+∠AEB)+∠DAE,求出∠DCE的度数是多少即可.
③根据∠BG1C=(∠ABD+∠ACD)+∠A,∠BG1C=70°,设∠A为x°,可得∠ABD+∠ACD=133°﹣x°,解方程,求出x的值,即可判断出∠A的度数是多少.
【解答】解:(1)如图(1),连接AD并延长至点F,
,
根据外角的性质,可得
∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,
又∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,
∴∠BDC=∠A+∠B+∠C;
(2)①由(1),可得
∠ABX+∠ACX+∠A=∠BXC,
∵∠A=40°,∠BXC=90°,
∴∠ABX+∠ACX=90°﹣40°=50°,
故答案为:50.
②由(1),可得
∠DBE=∠DAE+∠ADB+∠AEB,
∴∠ADB+∠AEB=∠DBE﹣∠DAE=130°﹣40°=90°,
∴(∠ADB+∠AEB)=90°÷2=45°,
∴∠DCE=(∠ADB+∠AEB)+∠DAE
=45°+40°
=85°;
③∠BG1C=(∠ABD+∠ACD)+∠A,
∵∠BG1C=70°,
∴设∠A为x°,
∵∠ABD+∠ACD=133°﹣x°
∴(133﹣x)+x=70,
∴13.3﹣x+x=70,
解得x=63,
即∠A的度数为63°.
【点评】此题主要考查了三角形的内角和定理,利用三角形的内角和定理和外角的性质是解答此题的关键.
第21页(共21页)
一、选择题。
1.已知△ABC,
(1)如图1,若A1点是∠ABC和∠ACD的角平分线的交点,则∠A1=∠A;
(2)如图2,若F点是∠ABC和∠DCE的角平分线的交点,则∠F=(∠A+∠D)﹣90°;
(3)如图3,若A1点是∠ABC和∠ACD的角平分线的交点,E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,则∠Q﹣∠A1=90°.
上述说法正确的个数是( )
A.0个 B.1个 C.2个 D.3个
2.在△ABC中,如果∠A﹣∠B=90°,那么△ABC是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.以上三种都可能
3.如图,将一副三角板按如图方式叠放,则角α等于( )
A.165° B.135° C.105° D.75°
4.如图,在△ABC中,∠C=78°,沿图中虚线截去∠C,则∠1+∠2=( )
A.282° B.180° C.360° D.258°
5.等腰三角形的一个内角是100°,它的另外两个角的度数是( )
A.50° 和 50° B.40° 和 40° C.35° 和 35° D.60° 和20°
二、填空题。
6.如图,在三角形ABC中,AD⊥BC,垂足为点D,直线EF过点C,且90°﹣∠FCB=∠BAD,点G为线段AB上一点,连接CG,∠BCG与∠BCE的角平分线CM、CN分别交AD于点M、N,若∠BGC=70°,则∠MCN= °.
7.已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC= .(用α,β表示)
8.在△ABC中,∠A=36°,当∠C= ,△ABC为等腰三角形.
9.如图1,在△ABC中,∠ABC,∠ACB的角平分线交于点O,则∠BOC=90°+∠A=×180°+∠A.如图2,在△ABC中,∠ABC,∠ACB的两条三等分角线分别对应交于O1,O2,则∠BO1C=×180°+∠A,∠BO2C=×180°+∠A.根据以上阅读理解,你能猜想∠BO2018C= .
10.如图,在△ABC中,点D、E分别在边BC、AC上,∠DCE=∠DEC,点F在AC、点G在DE的延长线上,∠DFG=∠DGF.若∠EFG=35°,则∠CDF的度数为 .
三、解答题。
11.如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.
(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE= 度;
(2)若图1中的∠B=x,∠ACB=y,则∠CFE= ;(用含x、y的代数式表示)
(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.
12.已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,DF恰好分别经过点B、C.
(1)∠DBC+∠DCB= 度;
(2)过点A作直线直线MN∥DE,若∠ACD=20°,试求∠CAM的大小.
13.如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠DAE、∠BOA的度数.
14.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=42°.
(1)求∠BOC的度数;
(2)把(1)中∠A=42°这个条件去掉,试探索∠BOC和∠A之间有怎样的数量关系.
15.探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
《三角形的内角》拓展练习
参考答案与试题解析
一、选择题。
1.已知△ABC,
(1)如图1,若A1点是∠ABC和∠ACD的角平分线的交点,则∠A1=∠A;
(2)如图2,若F点是∠ABC和∠DCE的角平分线的交点,则∠F=(∠A+∠D)﹣90°;
(3)如图3,若A1点是∠ABC和∠ACD的角平分线的交点,E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,则∠Q﹣∠A1=90°.
上述说法正确的个数是( )
A.0个 B.1个 C.2个 D.3个
【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,根据角平分线的定义可得∠A1CD=∠ACD,∠A1BC=∠ABC,然后整理即可得到∠A1=∠A;
(2)①根据四边形的内角和定理表示出∠BCD,再表示出∠DCE,然后根据角平分线的定义可得∠FBC=∠ABC,∠FCE=∠DCE,三角形的一个外角等于与它不相邻的两个内角的和可得∠F+∠FBC=∠FCE,然后整理即可得解;
(3)根据三角形的内角和定理表示出∠ACE+∠AEC,再根据角平分线的定义表示出∠QCE+∠QEC,然后利用三角形的内角和定理列式整理即可得解.
【解答】解:(1)由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∵∠ABC的角平分线与∠ACB的外角平分线交于A1,
∴∠A1CD=∠ACD,∠A1BC=∠ABC,
∴∠A1+∠A1BC=(∠A+∠ABC)=∠A+∠ABC,
∴∠A1=∠A;
(2)由四边形内角和定理得,∠BCD=360°﹣∠A﹣∠D﹣∠ABC,
∴∠DCE=180°﹣(360°﹣∠A﹣∠D﹣∠ABC)=∠A+∠D+∠ABC﹣180°,
由三角形的外角性质得,∠FCE=∠F+∠FBC,
∵BF、CF分别是∠ABC和∠DCE的平分线,
∴∠FBC=∠ABC,∠FCE=∠DCE,
∴∠F+∠FBC=(∠A+∠D+∠ABC﹣180°)=(∠A+∠D)+∠ABC﹣90°,
∴∠F=(∠A+∠D)﹣90°,
(3)∵EQ、CQ分别为∠AEC、∠ACE的角平分线,
∴∠QEC=∠AEC,∠QCE=∠ACE,
又∵∠AEC+∠ACE=∠BAC,
∴∠Q=180°﹣(∠QEC+∠QCE)=180°﹣(∠AEC+∠ACE),
=180°﹣∠BAC,
由(1)可知∠BAC=2∠A1,
∴∠Q=180°﹣∠A1,
∴∠Q+∠A1=180°.
故(1)(2)正确;
故选:C.
【点评】本题考查了三角形的内角和定理,角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键,要注意整体思想的利用.
2.在△ABC中,如果∠A﹣∠B=90°,那么△ABC是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.以上三种都可能
【分析】根据三角形内角和定理以及三角形的分类可知.
【解答】解:∵∠A﹣∠B=90°,
∴∠A=90°+∠B,
∴∠A大于90°.
根据三角形性质可知大于90°的角为钝角,
∴此三角形为钝角三角形.
故选:B.
【点评】本题考查的是三角形内角和定理,熟练掌握三角形的内角和是解题的关键.
3.如图,将一副三角板按如图方式叠放,则角α等于( )
A.165° B.135° C.105° D.75°
【分析】根据三角形内角和定理求出∠1,根据三角形外角的性质求出∠2,根据邻补角的概念计算即可.
【解答】解:∠1=90°﹣30°﹣60°,
∴∠2=∠1﹣45°=15°,
∴∠α=180°﹣15°=165°,
故选:A.
【点评】本题考查的是三角形内角和定理和三角形的外角的性质,掌握三角形内角和等于180°是解题的关键.
4.如图,在△ABC中,∠C=78°,沿图中虚线截去∠C,则∠1+∠2=( )
A.282° B.180° C.360° D.258°
【分析】根据三角形内角和定理求出∠3+∠4,根据邻补角的概念计算即可.
【解答】解:∵∠C=78°,
∴∠3+∠4=180°﹣78°=102°,
∴∠1+∠2=360°﹣(∠3+∠4)=258°,
故选:D.
【点评】本题考查的是三角形内角和定理,掌握三角形内角和等于180°是解题的关键.
5.等腰三角形的一个内角是100°,它的另外两个角的度数是( )
A.50° 和 50° B.40° 和 40° C.35° 和 35° D.60° 和20°
【分析】先判断出100°的角是顶角,再根据等腰三角形的两底角相等解答.
【解答】解:∵等腰三角形的一个角100°,
∴100°的角是顶角,
∴另两个底角都是(180°﹣100°)=40°,
故选:B.
【点评】本题考查了等腰三角形的性质,主要利用了等腰三角形两底角相等,需要注意100°的角不可能是底角.
二、填空题。
6.如图,在三角形ABC中,AD⊥BC,垂足为点D,直线EF过点C,且90°﹣∠FCB=∠BAD,点G为线段AB上一点,连接CG,∠BCG与∠BCE的角平分线CM、CN分别交AD于点M、N,若∠BGC=70°,则∠MCN= 35 °.
【分析】依据90°﹣∠B=∠BAD,90°﹣∠FCB=∠BAD,可得∠FCB=∠B,进而判定EF∥AB,即可得到∠ECG=∠BGC=70°,再根据∠MCN=∠BCN﹣∠BCM=(∠BCE﹣∠BCG)=∠ECG,即可得到结论.
【解答】解:∵AD⊥BC,
∴Rt△ABD中,90°﹣∠B=∠BAD,
又∵90°﹣∠FCB=∠BAD,
∴∠FCB=∠B,
∴EF∥AB,
∴∠ECG=∠BGC=70°,
∵∠BCG与∠BCE的角平分线CM、CN分别交AD于点M、N,
∴∠BCN=∠BCE,∠BCM=∠BCG,
∴∠MCN=∠BCN﹣∠BCM=(∠BCE﹣∠BCG)=∠ECG=×70°=35°,
故答案为:35.
【点评】本题考查了平行线的性质和判定以及角平分线的定义的综合运用,解题时注意平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.
7.已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC= (α+β) .(用α,β表示)
【分析】连接BC,根据角平分线的性质得到∠3=ABP,∠4=ACP,根据三角形的内角和得到∠1+∠2=180°﹣β,2(∠3+∠4)+(∠1+∠2)=180°﹣α,求出∠3+∠4=(β﹣α),根据三角形的内角和即可得到结论.
【解答】解:连接BC,
∵BQ平分∠ABP,CQ平分∠ACP,
∴∠3=ABP,∠4=ACP,
∵∠1+∠2=180°﹣β,2(∠3+∠4)+(∠1+∠2)=180°﹣α,
∴∠3+∠4=(β﹣α),
∵∠BQC=180°﹣(∠1+∠2)﹣(∠3+∠4)=180°﹣(180°﹣β)﹣(β﹣α),
即:∠BQC=(α+β).
故答案为:(α+β).
【点评】本题考查了三角形的内角和,角平分线的定义,连接BC构造三角形是解题的关键.
8.在△ABC中,∠A=36°,当∠C= 72°,36°,108° ,△ABC为等腰三角形.
【分析】分三种情形分别讨论,运用三角形内角和定理即可解决问题
【解答】解:①当AB=AC时,
∵∠A=36°,
∴∠C=∠B=72°.
②当CA=CB时,
∵∠A=∠B=36°,
∴∠C=108°.
③当BA=BC时,
∴∠C=∠A=36°,
综上所述,∠C的值为72°或108°或36°,
故答案为:72°,36°,108°.
【点评】本题考查等腰三角形的判定和性质以及三角形内角和定理的运用,解题的关键是用分类讨论的思想思考问题.
9.如图1,在△ABC中,∠ABC,∠ACB的角平分线交于点O,则∠BOC=90°+∠A=×180°+∠A.如图2,在△ABC中,∠ABC,∠ACB的两条三等分角线分别对应交于O1,O2,则∠BO1C=×180°+∠A,∠BO2C=×180°+∠A.根据以上阅读理解,你能猜想∠BO2018C= +∠A .
【分析】根据已知中的特例,观察两部分前边的倍数和n等分线间的关系,从而写出结论.
【解答】解:如图3,根据题中所给的信息,总结可得:
∠BO1C=×180°+∠A,
∠BOn﹣1C=×180°+∠A.
∴当n﹣1=2018时,n=2019,即∠BO2018C=+∠A.
故答案为:+∠A.
【点评】本题考查了三角形的内角和定理,综合运用了三角形的内角和定理和n等分角的概念,注意由特殊到一般的总结.
10.如图,在△ABC中,点D、E分别在边BC、AC上,∠DCE=∠DEC,点F在AC、点G在DE的延长线上,∠DFG=∠DGF.若∠EFG=35°,则∠CDF的度数为 70° .
【分析】根据三角形内角和定理求出x+y=145,在△FDC中,根据三角形内角和定理求出即可.
【解答】解:∵∠DCE=∠DEC,∠DFG=∠DGF,
∴设∠DCE=∠DEC=x°,∠DFG=∠DGF=y°,
则∠FEG=∠DEC=x°,
∵在△GFE中,∠EFG=35°,
∴∠FEG+∠DGF=x°+y°=180°﹣35°=145°,
即x+y=145,
在△FDC中,∠CDF=180°﹣∠DCE﹣∠DFC=180°﹣x°﹣(y°﹣35°)
=215°﹣(x°+y°)
=70°,
故答案为:70°.
【点评】本题考查了三角形内角和定理,能求出x+y=145是解此题的关键.
三、解答题。
11.如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.
(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE= 20 度;
(2)若图1中的∠B=x,∠ACB=y,则∠CFE= y﹣x ;(用含x、y的代数式表示)
(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.
【分析】(1)求∠CFE的度数,求出∠DAE的度数即可,只要求出∠BAE﹣∠BAD的度数,由平分和垂直易得∠BAE和∠BAD的度数即可;
(2)由(1)类推得出答案即可;
(3)类比以上思路,把问题转换为∠CFE=90°﹣∠ECF即可解决问题.
【解答】解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°﹣∠B﹣∠ACB=80°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵AE⊥BC,
∴∠AEB=90°
∴∠BAE=60°
∴∠DAE=∠BAE﹣∠BAD=60°﹣40°=20°,
∵CF∥AD,
∴∠CFE=∠DAE=20°;
故答案为:20;
(2)∵∠BAE=90°﹣∠B,∠BAD=∠BAC=(180°﹣∠B﹣∠BCA),
∴∠CFE=∠DAE=∠BAE﹣∠BAD=90°﹣∠B﹣(180°﹣∠B﹣∠BCA)=(∠BCA﹣∠B)=y﹣x.
故答案为:y﹣x;
(3)(2)中的结论成立.
∵∠B=x,∠ACB=y,
∴∠BAC=180°﹣x﹣y,
∵AD平分∠BAC,
∴∠DAC=∠BAC=90°﹣x﹣y,
∵CF∥AD,
∴∠ACF=∠DAC=90°﹣x﹣y,
∴∠BCF=y+90°﹣x﹣y=90°﹣x+y,
∴∠ECF=180°﹣∠BCF=90°+x﹣y,
∵AE⊥BC,
∴∠FEC=90°,
∴∠CFE=90°﹣∠ECF=y﹣x.
【点评】此题考查三角形的内角和定理,角平分线的性质,平行线的性质以及垂直的意义等知识,结合图形,灵活选择适当的方法解决问题.
12.已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,DF恰好分别经过点B、C.
(1)∠DBC+∠DCB= 90 度;
(2)过点A作直线直线MN∥DE,若∠ACD=20°,试求∠CAM的大小.
【分析】(1)在△DBC中,根据三角形内角和定理得∠DBC+∠DCB+∠D=180°,然后把∠D=90°代入计算即可;
(2)在Rt△ABC中,根据三角形内角和定理得∠ABC+∠ACB+∠A=180°,即,∴∠ABD+∠BAC=90°﹣∠ACD=70°,整体代入即可得出结论.
【解答】解:(1)在△DBC中,∵∠DBC+∠DCB+∠D=180°,
而∠D=90°,
∴∠DBC+∠DCB=90°;
故答案为90;
(2)在△ABC中,
∵∠ABC+∠ACB+∠A=180°,
即∠ABD+∠DBC+∠DCB+∠ACD+∠BAC=180°,
而∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=90°﹣∠BAC,
∴∠ABD+∠BAC=90°﹣∠ACD=70°.
又∵MN∥DE,
∴∠ABD=∠BAN.
而∠BAN+∠BAC+∠CAM=180°,
∴∠ABD+∠BAC+∠CAM=180°,
∴∠CAM=180°﹣(∠ABD+∠BAC)=110°.
【点评】此题主要考查了三角形内角和定理,平行线的性质,解本题的关键是求出∠ABD+∠BAC=70°.
13.如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠DAE、∠BOA的度数.
【分析】根据垂直的定义、角平分线的定义、三角形内角和定理计算即可.
【解答】解∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°﹣90°﹣70°=20°,
∵∠BAC=60°,AE是∠BAC的角平分线,
∴∠EAC=∠BAE=30°,
∴∠EAD=∠EAC﹣∠CAD=30°﹣20°=10°,
∠ABC=180°﹣∠BAC﹣∠C=50°,
∵BF是∠ABC的角平分线,
∴∠ABO=25°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣30°﹣25°=125°.
故∠DAE,∠BOA的度数分别是10°,125°.
【点评】本题考查的是三角形内角和定理、三角形的高和角平分线的定义,掌握三角形内角和等于180°是解题的关键.
14.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=42°.
(1)求∠BOC的度数;
(2)把(1)中∠A=42°这个条件去掉,试探索∠BOC和∠A之间有怎样的数量关系.
【分析】(1)先求出∠ABC+∠ACB的度数,根据平分线的定义得出∠1=∠ABC,∠2=∠ACB,求出∠1+∠2的度数,根据三角形内角和定理求出∠BOC即可;
(2)根据角平分线的定义可得∠1=∠ABC,∠2=∠ACB,然后用∠A表示出∠1+∠2,再根据三角形的内角和等于180°列式整理即可得出结论.
【解答】解:(1)∵∠A=42°,
∴∠ABC+∠ACB=180°﹣∠A=138°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠1=∠ABC,∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB)==69°,
∴∠BOC=180°﹣(∠1+∠2)=180°﹣69°=111°;
(2)∠BOC=90°+∠A,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠1=∠ABC,∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB)=(180°﹣∠A),
∴∠BOC=180°﹣(∠1+∠2)=180=90.
【点评】本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.
15.探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX= 50 °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
【分析】(1)首先连接AD并延长至点F,然后根据外角的性质,即可判断出∠BDC=∠A+∠B+∠C.
(2)①由(1)可得∠ABX+∠ACX+∠A=∠BXC,然后根据∠A=40°,∠BXC=90°,求出∠ABX+∠ACX的值是多少即可.
②由(1)可得∠DBE=∠DAE+∠ADB+∠AEB,再根据∠DAE=40°,∠DBE=130°,求出∠ADB+∠AEB的值是多少;然后根据∠DCE=(∠ADB+∠AEB)+∠DAE,求出∠DCE的度数是多少即可.
③根据∠BG1C=(∠ABD+∠ACD)+∠A,∠BG1C=70°,设∠A为x°,可得∠ABD+∠ACD=133°﹣x°,解方程,求出x的值,即可判断出∠A的度数是多少.
【解答】解:(1)如图(1),连接AD并延长至点F,
,
根据外角的性质,可得
∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,
又∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,
∴∠BDC=∠A+∠B+∠C;
(2)①由(1),可得
∠ABX+∠ACX+∠A=∠BXC,
∵∠A=40°,∠BXC=90°,
∴∠ABX+∠ACX=90°﹣40°=50°,
故答案为:50.
②由(1),可得
∠DBE=∠DAE+∠ADB+∠AEB,
∴∠ADB+∠AEB=∠DBE﹣∠DAE=130°﹣40°=90°,
∴(∠ADB+∠AEB)=90°÷2=45°,
∴∠DCE=(∠ADB+∠AEB)+∠DAE
=45°+40°
=85°;
③∠BG1C=(∠ABD+∠ACD)+∠A,
∵∠BG1C=70°,
∴设∠A为x°,
∵∠ABD+∠ACD=133°﹣x°
∴(133﹣x)+x=70,
∴13.3﹣x+x=70,
解得x=63,
即∠A的度数为63°.
【点评】此题主要考查了三角形的内角和定理,利用三角形的内角和定理和外角的性质是解答此题的关键.
第21页(共21页)
