人教版八年级上册数学 11.2.1 三角形的内角 拔高练习(word版含解析)
文档属性
| 名称 | 人教版八年级上册数学 11.2.1 三角形的内角 拔高练习(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 221.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 20:22:50 | ||
图片预览




文档简介
《 三角形的内角》拔高练习
一、选择题。
1.如图,在△ABC中,点D是∠ABC和∠ACB角平分线的交点,若∠BDC=110°,那么∠A=( )
A.40° B.50° C.60° D.70°
2.已知△ABC中,∠A比它相邻的外角小10°,则∠B+∠C为( )
A.85° B.95° C.100° D.110°
3.如图在△ABC中,D是AB上一点,E是AC上一点,BE,CD相交于点F,∠A=70°,∠ACD=20°,∠ABE=32°,则∠CFE的度数为( )
A.68° B.58° C.52° D.48°
4.下面给出的四个三角形都有一部分被遮挡,其中不能确定三角形类型的是( )
A. B.
C. D.
5.已知:如图,在△ABC中,∠A=60°,∠C=70°,点D、E分别在AB和AC上,且DE∥BC.则∠ADE的度数是( )
A.40° B.50° C.60° D.70°
二、填空题。
6.已知:△ABC中,∠A+∠B=∠C,则∠C= .
7.如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°,则∠BEC= 度.
8.如图,在△ABC中,∠B=60°,AD平分∠BAC,点E在AD延长线上,且EC⊥AC.若∠E=50°,则∠ADC的度数是 .
9.如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A= .
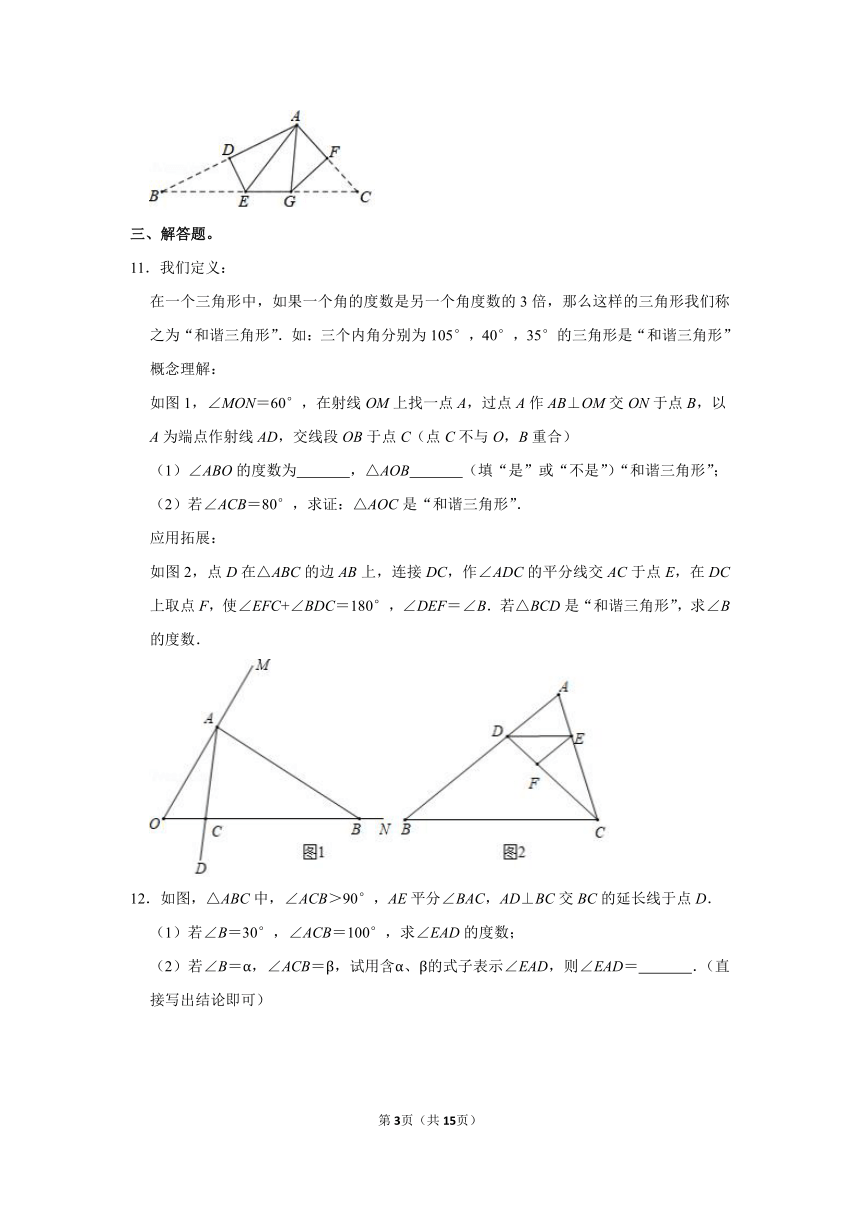
10.如图,将三角形纸片(△ABC)进行折叠,使得点B与点A重合,点C与点A重合,压平出现折痕DE,FG,其中D,F分别在边AB,AC上,E,G在边BC上,若∠B=25°,∠C=45°,则∠EAG的度数是 °.
三、解答题。
11.我们定义:
在一个三角形中,如果一个角的度数是另一个角度数的3倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为105°,40°,35°的三角形是“和谐三角形”
概念理解:
如图1,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O,B重合)
(1)∠ABO的度数为 ,△AOB (填“是”或“不是”)“和谐三角形”;
(2)若∠ACB=80°,求证:△AOC是“和谐三角形”.
应用拓展:
如图2,点D在△ABC的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC上取点F,使∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“和谐三角形”,求∠B的度数.
12.如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD,则∠EAD= .(直接写出结论即可)
13.如图,在△ABC中,D是BC边上一点,∠1=∠2=39°,∠3=∠4,求∠DAC的度数.
14.如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,试求∠EAD+∠ACD的度数.
15.如图,△ABC中,AD⊥BC于点D,AE是∠BAC的平分线,∠B=30°,∠C=70°,分别求:
(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
《 三角形的内角》拔高练习
参考答案与试题解析
一、选择题。
1.如图,在△ABC中,点D是∠ABC和∠ACB角平分线的交点,若∠BDC=110°,那么∠A=( )
A.40° B.50° C.60° D.70°
【分析】求出∠ABC+∠ACB的度数即可解决问题.
【解答】解:∵∠BDC=110°,
∴∠DBC+∠DCB=70°,
∵点D是∠ABC和∠ACB角平分线的交点,
∴∠ABC+∠ACB=2(∠DBC+∠DCB)=140°,
∴∠A=180°﹣140°=40°,
故选:A.
【点评】本题考查三角形的内角和定理,角平分线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
2.已知△ABC中,∠A比它相邻的外角小10°,则∠B+∠C为( )
A.85° B.95° C.100° D.110°
【分析】设∠A=x°.构建方程求出x,再利用三角形的内角和定理即可解决问题.
【解答】解:设∠A=x°.
由题意:180﹣x﹣x=10,
解得x=85°,
∴∠A=85°,
∴∠B+∠C=180°﹣85°=95°,
故选:B.
【点评】本题考查三角形的内角和定理,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
3.如图在△ABC中,D是AB上一点,E是AC上一点,BE,CD相交于点F,∠A=70°,∠ACD=20°,∠ABE=32°,则∠CFE的度数为( )
A.68° B.58° C.52° D.48°
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BDF=∠A+∠ACD,再根据三角形的内角和定理求出∠BFD,然后根据对顶角相等解答.
【解答】解:∵∠A=70°,∠ACD=20°,
∴∠BDF=∠A+∠ACD=70°+20°=90°,
在△BDF中,∠BFD=180°﹣∠BDF﹣∠ABE=180°﹣90°﹣32°=58°,
∴∠CFE=∠BFD=58°.
故选:B.
【点评】本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.
4.下面给出的四个三角形都有一部分被遮挡,其中不能确定三角形类型的是( )
A. B.
C. D.
【分析】根据三角形按角分类的方法一一判断即可.
【解答】解:观察图象可知:选项B,D的三角形是钝角三角形,选项C中的三角形是锐角三角形,
选项A中的三角形无法判定三角形的类型,
故选:A.
【点评】本题考查三角形的分类,解题的关键是熟练掌握基本知识,属于中考常考题型.
5.已知:如图,在△ABC中,∠A=60°,∠C=70°,点D、E分别在AB和AC上,且DE∥BC.则∠ADE的度数是( )
A.40° B.50° C.60° D.70°
【分析】根据三角形内角和定理求出∠B,再根据平行线的性质求出∠ADE即可.
【解答】解:在△ABC中,∵∠A=60°,∠C=70°,
∴∠B=180°﹣60°﹣70°=50°,
∵DE∥BC,
∴∠ADE=∠B=50°,
故选:B.
【点评】本题考查三角形内角和定理,平行线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
二、填空题。
6.已知:△ABC中,∠A+∠B=∠C,则∠C= 120° .
【分析】依据∠A+∠B=180°﹣∠C,∠A+∠B=∠C,即可得到180°﹣∠C=∠C,进而得出∠C的度数.
【解答】解:∵∠A+∠B=180°﹣∠C,∠A+∠B=∠C,
∴180°﹣∠C=∠C,
解得∠C=120°,
故答案为:120°.
【点评】本题主要考查了三角形内角和定理,解题时注意:三角形内角和是180°.
7.如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°,则∠BEC= 122 度.
【分析】根据三角形的内角和定理和角平分线的定义求得.
【解答】解:∵在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°.
∴∠EBC+∠ECB==58°,
∴∠BEC=180°﹣58°=122°;
故答案为:122.
【点评】本题考查了角平分线的定义,三角形的内角和,熟记三角形的内角和是解题的关键.
8.如图,在△ABC中,∠B=60°,AD平分∠BAC,点E在AD延长线上,且EC⊥AC.若∠E=50°,则∠ADC的度数是 100° .
【分析】根据三角形内角和和角平分线的定义解答即可.
【解答】解:∵EC⊥AC.∠E=50°,
∴∠DAC=40°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵∠B=60°,
∴∠ADC=40°+60°=100°,
故答案为:100°.
【点评】此题考查三角形内角和,关键是根据三角形内角和、三角形的外角性质和角平分线的定义解答.
9.如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A= 35° .
【分析】根据折叠的性质得到∠A′DE=∠ADE,∠A′ED=∠AED,由平角的定义得到∠BDA′+2∠ADE=180°,∠A′EC+2∠AED=180°,根据已知条件得到∠ADE+∠AED=140°,由三角形的内角和即可得到结论.
【解答】解:∵将△ABC沿着DE对折,A落到A′,
∴∠A′DE=∠ADE,∠A′ED=∠AED,
∴∠BDA′+2∠ADE=180°,∠A′EC+2∠AED=180°,
∴∠BDA′+2∠ADE+∠A′EC+2∠AED=360°,
∵∠BDA′+∠CEA′=70°,
∴∠ADE+∠AED=140°,
∴∠A=35°.
故答案为:35°.
【点评】本题考查图形的折叠变化及三角形的内角和定理.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
10.如图,将三角形纸片(△ABC)进行折叠,使得点B与点A重合,点C与点A重合,压平出现折痕DE,FG,其中D,F分别在边AB,AC上,E,G在边BC上,若∠B=25°,∠C=45°,则∠EAG的度数是 40 °.
【分析】依据三角形内角和定理,即可得到∠BAC的度数,再根据折叠的性质,即可得到∠BAE=∠B=25°,∠CAG=∠C=45°,进而得出∠EAG的度数.
【解答】解:∵∠B=25°,∠C=45°,
∴∠BAC=180°﹣25°﹣45°=110°,
由折叠可得,∠BAE=∠B=25°,∠CAG=∠C=45°,
∴∠EAG=110°﹣(25°+45°)=40°,
故答案为:40°.
【点评】本题主要考查了三角形内角和定理,解题时注意:三角形内角和是180°.
三、解答题。
11.我们定义:
在一个三角形中,如果一个角的度数是另一个角度数的3倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为105°,40°,35°的三角形是“和谐三角形”
概念理解:
如图1,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O,B重合)
(1)∠ABO的度数为 30° ,△AOB 是 (填“是”或“不是”)“和谐三角形”;
(2)若∠ACB=80°,求证:△AOC是“和谐三角形”.
应用拓展:
如图2,点D在△ABC的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC上取点F,使∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“和谐三角形”,求∠B的度数.
【分析】(1)根据垂直的定义、三角形内角和定理求出∠ABO的度数,根据“和谐三角形”的概念判断;
(2)根据“和谐三角形”的概念证明即可;
应用拓展:根据比较的性质得到∠EFC=∠ADC,根据平行线的性质得到∠DEF=∠ADE,推出DE∥BC,得到∠CDE=∠BCD,根据角平分线的定义得到∠ADE=∠CDE,求得∠B=∠BCD,根据“和谐三角形”的定义求解即可.
【解答】解:(1)∵AB⊥OM,
∴∠OAB=90°,
∴∠ABO=90°﹣∠MON=30°,
∵∠OAB=3∠ABO,
∴△AOB为“和谐三角形”,
故答案为:30;是;
(2)证明:∵∠MON=60°,∠ACB=80°,
∵∠ACB=∠OAC+∠MON,
∴∠OAC=80°﹣60°=20°,
∵∠AOB=60°=3×20°=3∠OAC,
∴△AOC是“和谐三角形”;
应用拓展:
∵∠EFC+∠BDC=180°,∠ADC+∠BDC=180°,
∴∠EFC=∠ADC,
∴AD∥EF,
∴∠DEF=∠ADE,
∵∠DEF=∠B,
∴∠B=∠ADE,
∴DE∥BC,
∴∠CDE=∠BCD,
∵AE平分∠ADC,
∴∠ADE=∠CDE,
∴∠B=∠BCD,
∵△BCD是“和谐三角形”,
∴∠BDC=3∠B,或∠B=3∠BDC,
∵∠BDC+∠BCD+∠B=180°,
∴∠B=36°或∠B=.
【点评】本题考查的是三角形内角和定理、“智慧三角形”的概念,用分类讨论的思想解决问题是解本题的关键.
12.如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD,则∠EAD= β﹣α .(直接写出结论即可)
【分析】(1)根据垂直的定义得到∠D=90°,根据邻补角的定义得到∠ACD=180°﹣100°=80°,根据三角形的内角和得到∠BAC=50°,根据角平分线的定义得到∠CAE=∠BAC=25°,于是得到结论;
(2)根据垂直的定义得到∠D=90°,得到∠ACD=180°﹣β,求得∠BAC=90°﹣α﹣(β﹣90°)=180°﹣α﹣β,根据角平分线的定义得到∠CAE=∠BAC=90°﹣(α+β),根据角的和差即可得到结论.
【解答】解:(1)∵AD⊥BC,
∴∠D=90°,
∵∠ACB=100°,
∴∠ACD=180°﹣100°=80°,
∴∠CAD=90°﹣80°=10°,
∵∠B=30°,
∴∠BAD=90°﹣30°=60°,
∴∠BAC=50°,
∵AE平分∠BAC,
∴∠CAE=∠BAC=25°,
∴∠EAD=∠CAE+∠CAD=35°;
(2)∵AD⊥BC,
∴∠D=90°,
∵∠ACB=β,
∴∠ACD=180°﹣β,
∴∠CAD=90°﹣∠ACD=β﹣90°,
∵∠B=α,
∴∠BAD=90°﹣α,
∴∠BAC=90°﹣α﹣(β﹣90°)=180°﹣α﹣β,
∵AE平分∠BAC,
∴∠CAE=∠BAC=90°﹣(α+β),
∴∠EAD=∠CAE+∠CAD=90°﹣(α+β)+β﹣90°=β﹣α.
故答案为:β﹣α.
【点评】本题考查了三角形的内角和,角平分线的定义,正确的识别图形是解题的关键.
13.如图,在△ABC中,D是BC边上一点,∠1=∠2=39°,∠3=∠4,求∠DAC的度数.
【分析】依据三角形外角性质,即可得到∠3的度数,再根据三角形内角和定理,即可得到∠DAC的度数.
【解答】解:∵∠1=∠2=39°,
∴∠3=∠4=∠1+∠2=78°,
∴△ACD中,∠DAC=180°﹣(∠3+∠4)=180°﹣2×78°=24°.
【点评】本题主要考查了三角形内角和定理以及三角形外角性质的综合应用,解题时注意:三角形的一个外角等于和它不相邻的两个内角的和.
14.如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,试求∠EAD+∠ACD的度数.
【分析】依据AD是BC边上的高,∠ABC=60°,即可得到∠BAD=30°,依据∠BAC=50°,AE平分∠BAC,即可得到∠DAE=5°,再根据△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,可得∠EAD+∠ACD=75°.
【解答】解:∵AD是BC边上的高,∠ABC=60°,
∴∠BAD=30°,
∵∠BAC=50°,AE平分∠BAC,
∴∠BAE=25°,
∴∠DAE=30°﹣25°=5°,
∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,
∴∠EAD+∠ACD=5°+70°=75°.
【点评】本题考查了三角形内角和定理:三角形内角和为180°.解决问题的关键是三角形外角性质以及角平分线的定义的运用.
15.如图,△ABC中,AD⊥BC于点D,AE是∠BAC的平分线,∠B=30°,∠C=70°,分别求:
(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
【分析】(1)根据三角形的内角和即可得到结论;
(2)根据角平分线的定义得到∠BAE=∠BAC=40°,根据三角形的外角的性质即可得到结论;
(3)根据垂直的定义得到∠ADE=90°,根据三角形的内角和即可得到结论..
【解答】解:(1)∵∠B=30°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=80°;
(2)∵AE是∠BAC的平分线,
∴∠BAE=∠BAC=40°,
∴∠AED=∠BAE+∠B=40°+30°=70°;
(3)∵AD⊥BC,
∴∠ADE=90°,
∴∠EAD=∠ADE﹣AED=90°﹣70°=20°.
【点评】本题考查了三角形的内角和,角平分线的定义,熟练掌握三角形的内角和是解题的关键.
第17页(共17页)
一、选择题。
1.如图,在△ABC中,点D是∠ABC和∠ACB角平分线的交点,若∠BDC=110°,那么∠A=( )
A.40° B.50° C.60° D.70°
2.已知△ABC中,∠A比它相邻的外角小10°,则∠B+∠C为( )
A.85° B.95° C.100° D.110°
3.如图在△ABC中,D是AB上一点,E是AC上一点,BE,CD相交于点F,∠A=70°,∠ACD=20°,∠ABE=32°,则∠CFE的度数为( )
A.68° B.58° C.52° D.48°
4.下面给出的四个三角形都有一部分被遮挡,其中不能确定三角形类型的是( )
A. B.
C. D.
5.已知:如图,在△ABC中,∠A=60°,∠C=70°,点D、E分别在AB和AC上,且DE∥BC.则∠ADE的度数是( )
A.40° B.50° C.60° D.70°
二、填空题。
6.已知:△ABC中,∠A+∠B=∠C,则∠C= .
7.如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°,则∠BEC= 度.
8.如图,在△ABC中,∠B=60°,AD平分∠BAC,点E在AD延长线上,且EC⊥AC.若∠E=50°,则∠ADC的度数是 .
9.如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A= .
10.如图,将三角形纸片(△ABC)进行折叠,使得点B与点A重合,点C与点A重合,压平出现折痕DE,FG,其中D,F分别在边AB,AC上,E,G在边BC上,若∠B=25°,∠C=45°,则∠EAG的度数是 °.
三、解答题。
11.我们定义:
在一个三角形中,如果一个角的度数是另一个角度数的3倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为105°,40°,35°的三角形是“和谐三角形”
概念理解:
如图1,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O,B重合)
(1)∠ABO的度数为 ,△AOB (填“是”或“不是”)“和谐三角形”;
(2)若∠ACB=80°,求证:△AOC是“和谐三角形”.
应用拓展:
如图2,点D在△ABC的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC上取点F,使∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“和谐三角形”,求∠B的度数.
12.如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD,则∠EAD= .(直接写出结论即可)
13.如图,在△ABC中,D是BC边上一点,∠1=∠2=39°,∠3=∠4,求∠DAC的度数.
14.如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,试求∠EAD+∠ACD的度数.
15.如图,△ABC中,AD⊥BC于点D,AE是∠BAC的平分线,∠B=30°,∠C=70°,分别求:
(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
《 三角形的内角》拔高练习
参考答案与试题解析
一、选择题。
1.如图,在△ABC中,点D是∠ABC和∠ACB角平分线的交点,若∠BDC=110°,那么∠A=( )
A.40° B.50° C.60° D.70°
【分析】求出∠ABC+∠ACB的度数即可解决问题.
【解答】解:∵∠BDC=110°,
∴∠DBC+∠DCB=70°,
∵点D是∠ABC和∠ACB角平分线的交点,
∴∠ABC+∠ACB=2(∠DBC+∠DCB)=140°,
∴∠A=180°﹣140°=40°,
故选:A.
【点评】本题考查三角形的内角和定理,角平分线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
2.已知△ABC中,∠A比它相邻的外角小10°,则∠B+∠C为( )
A.85° B.95° C.100° D.110°
【分析】设∠A=x°.构建方程求出x,再利用三角形的内角和定理即可解决问题.
【解答】解:设∠A=x°.
由题意:180﹣x﹣x=10,
解得x=85°,
∴∠A=85°,
∴∠B+∠C=180°﹣85°=95°,
故选:B.
【点评】本题考查三角形的内角和定理,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
3.如图在△ABC中,D是AB上一点,E是AC上一点,BE,CD相交于点F,∠A=70°,∠ACD=20°,∠ABE=32°,则∠CFE的度数为( )
A.68° B.58° C.52° D.48°
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BDF=∠A+∠ACD,再根据三角形的内角和定理求出∠BFD,然后根据对顶角相等解答.
【解答】解:∵∠A=70°,∠ACD=20°,
∴∠BDF=∠A+∠ACD=70°+20°=90°,
在△BDF中,∠BFD=180°﹣∠BDF﹣∠ABE=180°﹣90°﹣32°=58°,
∴∠CFE=∠BFD=58°.
故选:B.
【点评】本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.
4.下面给出的四个三角形都有一部分被遮挡,其中不能确定三角形类型的是( )
A. B.
C. D.
【分析】根据三角形按角分类的方法一一判断即可.
【解答】解:观察图象可知:选项B,D的三角形是钝角三角形,选项C中的三角形是锐角三角形,
选项A中的三角形无法判定三角形的类型,
故选:A.
【点评】本题考查三角形的分类,解题的关键是熟练掌握基本知识,属于中考常考题型.
5.已知:如图,在△ABC中,∠A=60°,∠C=70°,点D、E分别在AB和AC上,且DE∥BC.则∠ADE的度数是( )
A.40° B.50° C.60° D.70°
【分析】根据三角形内角和定理求出∠B,再根据平行线的性质求出∠ADE即可.
【解答】解:在△ABC中,∵∠A=60°,∠C=70°,
∴∠B=180°﹣60°﹣70°=50°,
∵DE∥BC,
∴∠ADE=∠B=50°,
故选:B.
【点评】本题考查三角形内角和定理,平行线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
二、填空题。
6.已知:△ABC中,∠A+∠B=∠C,则∠C= 120° .
【分析】依据∠A+∠B=180°﹣∠C,∠A+∠B=∠C,即可得到180°﹣∠C=∠C,进而得出∠C的度数.
【解答】解:∵∠A+∠B=180°﹣∠C,∠A+∠B=∠C,
∴180°﹣∠C=∠C,
解得∠C=120°,
故答案为:120°.
【点评】本题主要考查了三角形内角和定理,解题时注意:三角形内角和是180°.
7.如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°,则∠BEC= 122 度.
【分析】根据三角形的内角和定理和角平分线的定义求得.
【解答】解:∵在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=64°.
∴∠EBC+∠ECB==58°,
∴∠BEC=180°﹣58°=122°;
故答案为:122.
【点评】本题考查了角平分线的定义,三角形的内角和,熟记三角形的内角和是解题的关键.
8.如图,在△ABC中,∠B=60°,AD平分∠BAC,点E在AD延长线上,且EC⊥AC.若∠E=50°,则∠ADC的度数是 100° .
【分析】根据三角形内角和和角平分线的定义解答即可.
【解答】解:∵EC⊥AC.∠E=50°,
∴∠DAC=40°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵∠B=60°,
∴∠ADC=40°+60°=100°,
故答案为:100°.
【点评】此题考查三角形内角和,关键是根据三角形内角和、三角形的外角性质和角平分线的定义解答.
9.如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A= 35° .
【分析】根据折叠的性质得到∠A′DE=∠ADE,∠A′ED=∠AED,由平角的定义得到∠BDA′+2∠ADE=180°,∠A′EC+2∠AED=180°,根据已知条件得到∠ADE+∠AED=140°,由三角形的内角和即可得到结论.
【解答】解:∵将△ABC沿着DE对折,A落到A′,
∴∠A′DE=∠ADE,∠A′ED=∠AED,
∴∠BDA′+2∠ADE=180°,∠A′EC+2∠AED=180°,
∴∠BDA′+2∠ADE+∠A′EC+2∠AED=360°,
∵∠BDA′+∠CEA′=70°,
∴∠ADE+∠AED=140°,
∴∠A=35°.
故答案为:35°.
【点评】本题考查图形的折叠变化及三角形的内角和定理.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
10.如图,将三角形纸片(△ABC)进行折叠,使得点B与点A重合,点C与点A重合,压平出现折痕DE,FG,其中D,F分别在边AB,AC上,E,G在边BC上,若∠B=25°,∠C=45°,则∠EAG的度数是 40 °.
【分析】依据三角形内角和定理,即可得到∠BAC的度数,再根据折叠的性质,即可得到∠BAE=∠B=25°,∠CAG=∠C=45°,进而得出∠EAG的度数.
【解答】解:∵∠B=25°,∠C=45°,
∴∠BAC=180°﹣25°﹣45°=110°,
由折叠可得,∠BAE=∠B=25°,∠CAG=∠C=45°,
∴∠EAG=110°﹣(25°+45°)=40°,
故答案为:40°.
【点评】本题主要考查了三角形内角和定理,解题时注意:三角形内角和是180°.
三、解答题。
11.我们定义:
在一个三角形中,如果一个角的度数是另一个角度数的3倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为105°,40°,35°的三角形是“和谐三角形”
概念理解:
如图1,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O,B重合)
(1)∠ABO的度数为 30° ,△AOB 是 (填“是”或“不是”)“和谐三角形”;
(2)若∠ACB=80°,求证:△AOC是“和谐三角形”.
应用拓展:
如图2,点D在△ABC的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC上取点F,使∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“和谐三角形”,求∠B的度数.
【分析】(1)根据垂直的定义、三角形内角和定理求出∠ABO的度数,根据“和谐三角形”的概念判断;
(2)根据“和谐三角形”的概念证明即可;
应用拓展:根据比较的性质得到∠EFC=∠ADC,根据平行线的性质得到∠DEF=∠ADE,推出DE∥BC,得到∠CDE=∠BCD,根据角平分线的定义得到∠ADE=∠CDE,求得∠B=∠BCD,根据“和谐三角形”的定义求解即可.
【解答】解:(1)∵AB⊥OM,
∴∠OAB=90°,
∴∠ABO=90°﹣∠MON=30°,
∵∠OAB=3∠ABO,
∴△AOB为“和谐三角形”,
故答案为:30;是;
(2)证明:∵∠MON=60°,∠ACB=80°,
∵∠ACB=∠OAC+∠MON,
∴∠OAC=80°﹣60°=20°,
∵∠AOB=60°=3×20°=3∠OAC,
∴△AOC是“和谐三角形”;
应用拓展:
∵∠EFC+∠BDC=180°,∠ADC+∠BDC=180°,
∴∠EFC=∠ADC,
∴AD∥EF,
∴∠DEF=∠ADE,
∵∠DEF=∠B,
∴∠B=∠ADE,
∴DE∥BC,
∴∠CDE=∠BCD,
∵AE平分∠ADC,
∴∠ADE=∠CDE,
∴∠B=∠BCD,
∵△BCD是“和谐三角形”,
∴∠BDC=3∠B,或∠B=3∠BDC,
∵∠BDC+∠BCD+∠B=180°,
∴∠B=36°或∠B=.
【点评】本题考查的是三角形内角和定理、“智慧三角形”的概念,用分类讨论的思想解决问题是解本题的关键.
12.如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD,则∠EAD= β﹣α .(直接写出结论即可)
【分析】(1)根据垂直的定义得到∠D=90°,根据邻补角的定义得到∠ACD=180°﹣100°=80°,根据三角形的内角和得到∠BAC=50°,根据角平分线的定义得到∠CAE=∠BAC=25°,于是得到结论;
(2)根据垂直的定义得到∠D=90°,得到∠ACD=180°﹣β,求得∠BAC=90°﹣α﹣(β﹣90°)=180°﹣α﹣β,根据角平分线的定义得到∠CAE=∠BAC=90°﹣(α+β),根据角的和差即可得到结论.
【解答】解:(1)∵AD⊥BC,
∴∠D=90°,
∵∠ACB=100°,
∴∠ACD=180°﹣100°=80°,
∴∠CAD=90°﹣80°=10°,
∵∠B=30°,
∴∠BAD=90°﹣30°=60°,
∴∠BAC=50°,
∵AE平分∠BAC,
∴∠CAE=∠BAC=25°,
∴∠EAD=∠CAE+∠CAD=35°;
(2)∵AD⊥BC,
∴∠D=90°,
∵∠ACB=β,
∴∠ACD=180°﹣β,
∴∠CAD=90°﹣∠ACD=β﹣90°,
∵∠B=α,
∴∠BAD=90°﹣α,
∴∠BAC=90°﹣α﹣(β﹣90°)=180°﹣α﹣β,
∵AE平分∠BAC,
∴∠CAE=∠BAC=90°﹣(α+β),
∴∠EAD=∠CAE+∠CAD=90°﹣(α+β)+β﹣90°=β﹣α.
故答案为:β﹣α.
【点评】本题考查了三角形的内角和,角平分线的定义,正确的识别图形是解题的关键.
13.如图,在△ABC中,D是BC边上一点,∠1=∠2=39°,∠3=∠4,求∠DAC的度数.
【分析】依据三角形外角性质,即可得到∠3的度数,再根据三角形内角和定理,即可得到∠DAC的度数.
【解答】解:∵∠1=∠2=39°,
∴∠3=∠4=∠1+∠2=78°,
∴△ACD中,∠DAC=180°﹣(∠3+∠4)=180°﹣2×78°=24°.
【点评】本题主要考查了三角形内角和定理以及三角形外角性质的综合应用,解题时注意:三角形的一个外角等于和它不相邻的两个内角的和.
14.如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,试求∠EAD+∠ACD的度数.
【分析】依据AD是BC边上的高,∠ABC=60°,即可得到∠BAD=30°,依据∠BAC=50°,AE平分∠BAC,即可得到∠DAE=5°,再根据△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,可得∠EAD+∠ACD=75°.
【解答】解:∵AD是BC边上的高,∠ABC=60°,
∴∠BAD=30°,
∵∠BAC=50°,AE平分∠BAC,
∴∠BAE=25°,
∴∠DAE=30°﹣25°=5°,
∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,
∴∠EAD+∠ACD=5°+70°=75°.
【点评】本题考查了三角形内角和定理:三角形内角和为180°.解决问题的关键是三角形外角性质以及角平分线的定义的运用.
15.如图,△ABC中,AD⊥BC于点D,AE是∠BAC的平分线,∠B=30°,∠C=70°,分别求:
(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
【分析】(1)根据三角形的内角和即可得到结论;
(2)根据角平分线的定义得到∠BAE=∠BAC=40°,根据三角形的外角的性质即可得到结论;
(3)根据垂直的定义得到∠ADE=90°,根据三角形的内角和即可得到结论..
【解答】解:(1)∵∠B=30°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=80°;
(2)∵AE是∠BAC的平分线,
∴∠BAE=∠BAC=40°,
∴∠AED=∠BAE+∠B=40°+30°=70°;
(3)∵AD⊥BC,
∴∠ADE=90°,
∴∠EAD=∠ADE﹣AED=90°﹣70°=20°.
【点评】本题考查了三角形的内角和,角平分线的定义,熟练掌握三角形的内角和是解题的关键.
第17页(共17页)
