北师大版数学八年级上册第3章 位置与坐标 复习课课件(共24张PPT)
文档属性
| 名称 | 北师大版数学八年级上册第3章 位置与坐标 复习课课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 358.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 19:24:47 | ||
图片预览







文档简介
(共24张PPT)
第三章 位置与坐标
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
1.坐标与图形位置:
(1)结合实例进一步体会有序数对可以表示物体的位置.
(2)理解平面直角坐标系的有关概念,能画出直角坐标系;在给定的直角坐标系中,能根据坐标描出点的位置、由点的位置写出它的坐标.
(3)在实际问题中,能建立适当的直角坐标系,描述物体的位置.
(4)对给定的正方形,会选择适当的直角坐标系,写出它的顶点坐标,体会可以用坐标刻画一个简单图形.
(5)在平面上,能用方位角和距离刻画两个物体的相对位置.
2.坐标与图形运动:在直角坐标系中,以坐标轴为对称轴,能写出一个已知顶点坐标的多边形的对称图形的顶点坐标,并知道对应顶点坐标之间的关系.
知识导航
位置与坐标 确定位置 条件:在平面内,确定一个物体的位置一般要有两个数据
方法:区域定位法、方格定位法、方位角+距离定位法、经纬度定位法
平面直角坐标系 概念:在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.水平的数轴叫做x轴或横轴,铅直的数轴叫做y轴或纵轴
点的表示:建立坐标系后,对于平面内任意一点P,都有唯一的一个有序实数对与之对应;反过来,对于任意一个有序实数对,都有平面上唯一的点与之对应
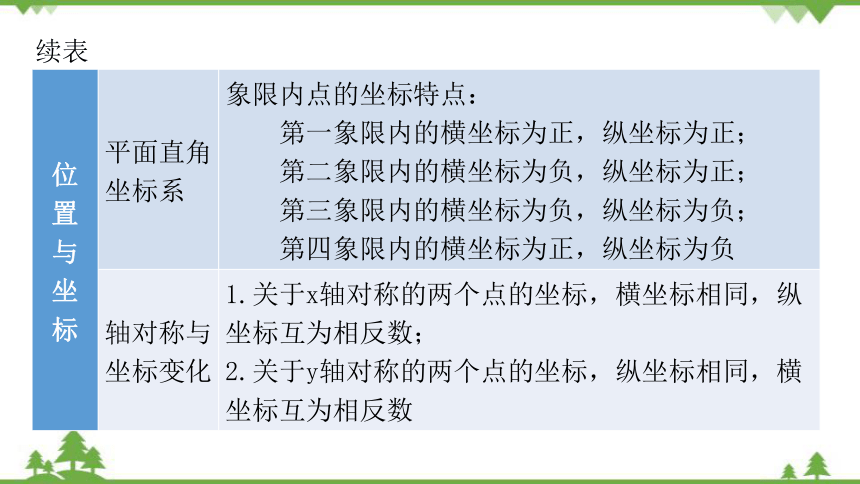
续表
位置与坐标 平面直角坐标系 象限内点的坐标特点:
第一象限内的横坐标为正,纵坐标为正;
第二象限内的横坐标为负,纵坐标为正;
第三象限内的横坐标为负,纵坐标为负;
第四象限内的横坐标为正,纵坐标为负
轴对称与坐标变化 1.关于x轴对称的两个点的坐标,横坐标相同,纵坐标互为相反数;
2.关于y轴对称的两个点的坐标,纵坐标相同,横坐标互为相反数
专题1 坐标与图形位置
1.(2020株洲)在平面直角坐标系中,点A(a,2)在第二象限内,则a的取值可以是( )
A. 1 B.
C. D. 4或-4
B
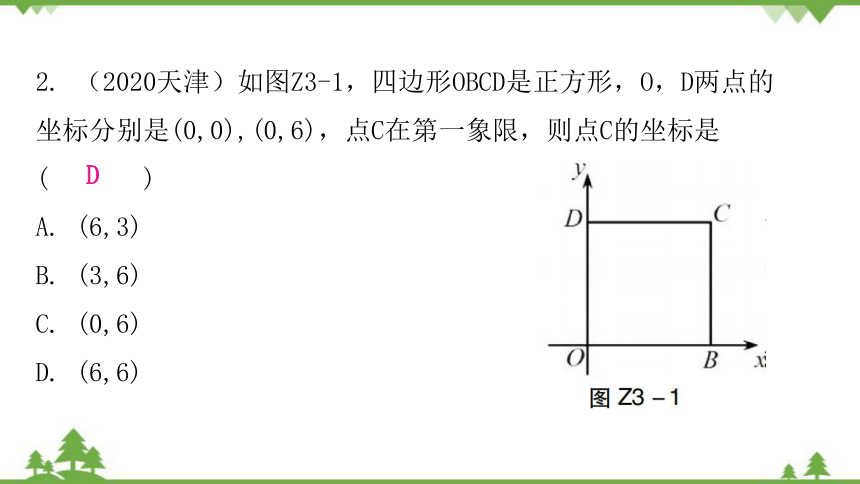
2. (2020天津)如图Z3-1,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A. (6,3)
B. (3,6)
C. (0,6)
D. (6,6)
D
3. 方格纸上有A,B两点,若以点B为原点建立直角坐标系,则点A的坐标为(3,4);若以点A为原点建立直角坐标系,则点B的坐标是( )
A.(3,4) B.(4,3)
C.(-3,-4) D.(-4,3)
C
4. (2020泰州)以水平数轴的原点O为圆心过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°,60°,90°,…,330°得到11条射线,构成如图Z3-2
所示的“圆”坐标系,点A,B的坐标
分别表示为(5,0°),(4,300°),
则点C的坐标表示为_______________.
(3,240°)
5. 如图Z3-3所示是某市区的部分平面示意图,为准确表示地理位置,可以建立平面直角坐标系用坐标表示地理位置.若交警大队的坐标是(5,3),中国银行的坐标是(4,1),则实验中学的坐标为____________.
(-2,1)
6.(1)写出如图Z3-4中点A,B,C,D,E,F的坐标;
(2)在图中描出下列各点:L(-5,-3),M(4,0),N(0,5),P(6,2).
解:(1)A(-2,-2),
B(-5,4),C(5,-4),
D(0,-3),E(2,5),
F(-3,0).
(2)略.
7. 已知:如图Z3-5,在△ABC中,AC=BC=5,AB=6,请以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,并求出△ABC的各顶点的坐标.
解:建立的直角坐标系如答图Z3-1.
过点C作CD⊥AB于点D,如答图Z3-1.
因为AC=BC=5,AB=6,
所以BD=AD= AB= ×6=3.
由勾股定理得CD= =4.
所以△ABC的各顶点坐标分别为A(0,0),
B(-6,0),C(-3,4).
1.点A(4,-2)关于x轴的对称点的坐标为( )
A.( 4,2 ) B.(-4,2)
C.(-4,-2) D.(-2,4)
2. (2020淮安)在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是( )
A. (2,3) B. (-3,2)
C. (-3,-2) D.(-2,-3)
专题2 轴对称与坐标变化
A
C
3. 如图Z3-6,将点A(-1,2)关于x轴作轴对称变换,则变换后点的坐标是( )
A.(1,2)
B.(1,-2)
C.(-1,-2)
D.(-2,-1)
C
4.已知△ABC在直角坐标系中的位置如图Z3-7,若△A′B′C′与△ABC关于y轴对称,则点A的对应点A′的坐标是( )
A.(-3,2) B.(3,2)
C.(-3,-2) D.(3,-2)
B
5. (2020达州)如图Z3-8,点P(-2,1)与点Q(a,b)关于直线l(y=-1)对称,则a+b=_________.
-5
6.如图Z3-9,已知在直角坐标系中,△OBC的顶点O(0,0),B(-6,0),且∠OCB=90°,OC=BC,则点C关于y轴的对称点C′的坐标是______________.
(3,3)
7. 在平面直角坐标系中,点M(a,b)与点N(3,-1)关于x轴对称,则a+b的值是_________.
8. 若点P(-2a,a-1)在y轴上,则点P的坐标为____________,点P关于x轴对称的点的坐标为____________.
4
(0,-1)
(0,1)
9.已知点P(a-1,-b+2)关于x轴的对称点为M,关于y轴的对称点为N,若点M与点N的坐标相同.
(1)求a,b的值;
(2)猜想点P的位置并说明理由.
解:(1)因为点P(a-1,-b+2)关于x轴的对称点为M,
所以M(a-1,b-2).
因为点P(a-1,-b+2)关于y轴的对称点为N,
所以N(-a+1,-b+2).
因为点M与点N的坐标相同,
所以a-1=-a+1,b-2=-b+2.
解得a=1,b=2.
(2)点P的位置是原点.理由如下.
因为a=1,b=2,
所以点P(a-1,-b+2)的坐标为(0,0),即点P为原点.
10.写出如图Z3-10中“小鱼”上所标各点的坐标并回答:
(1)点B,E的位置有什么特点?
(2)从点B与点E,点C与点D的位置看,它们的坐标有什么特点?
解:各点的坐标分别为A(-2,0),B(0,-2),
C(2,-1),D(2,1),E(0,2).
(1)点B(0,-2)和点E(0,2)关于x轴对称.
(2)点B(0,-2)与点E(0,2),点C(2,-1)
与点D(2,1),它们的横坐标相同,纵坐标互为
相反数.
谢 谢
第三章 位置与坐标
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
1.坐标与图形位置:
(1)结合实例进一步体会有序数对可以表示物体的位置.
(2)理解平面直角坐标系的有关概念,能画出直角坐标系;在给定的直角坐标系中,能根据坐标描出点的位置、由点的位置写出它的坐标.
(3)在实际问题中,能建立适当的直角坐标系,描述物体的位置.
(4)对给定的正方形,会选择适当的直角坐标系,写出它的顶点坐标,体会可以用坐标刻画一个简单图形.
(5)在平面上,能用方位角和距离刻画两个物体的相对位置.
2.坐标与图形运动:在直角坐标系中,以坐标轴为对称轴,能写出一个已知顶点坐标的多边形的对称图形的顶点坐标,并知道对应顶点坐标之间的关系.
知识导航
位置与坐标 确定位置 条件:在平面内,确定一个物体的位置一般要有两个数据
方法:区域定位法、方格定位法、方位角+距离定位法、经纬度定位法
平面直角坐标系 概念:在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.水平的数轴叫做x轴或横轴,铅直的数轴叫做y轴或纵轴
点的表示:建立坐标系后,对于平面内任意一点P,都有唯一的一个有序实数对与之对应;反过来,对于任意一个有序实数对,都有平面上唯一的点与之对应
续表
位置与坐标 平面直角坐标系 象限内点的坐标特点:
第一象限内的横坐标为正,纵坐标为正;
第二象限内的横坐标为负,纵坐标为正;
第三象限内的横坐标为负,纵坐标为负;
第四象限内的横坐标为正,纵坐标为负
轴对称与坐标变化 1.关于x轴对称的两个点的坐标,横坐标相同,纵坐标互为相反数;
2.关于y轴对称的两个点的坐标,纵坐标相同,横坐标互为相反数
专题1 坐标与图形位置
1.(2020株洲)在平面直角坐标系中,点A(a,2)在第二象限内,则a的取值可以是( )
A. 1 B.
C. D. 4或-4
B
2. (2020天津)如图Z3-1,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A. (6,3)
B. (3,6)
C. (0,6)
D. (6,6)
D
3. 方格纸上有A,B两点,若以点B为原点建立直角坐标系,则点A的坐标为(3,4);若以点A为原点建立直角坐标系,则点B的坐标是( )
A.(3,4) B.(4,3)
C.(-3,-4) D.(-4,3)
C
4. (2020泰州)以水平数轴的原点O为圆心过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°,60°,90°,…,330°得到11条射线,构成如图Z3-2
所示的“圆”坐标系,点A,B的坐标
分别表示为(5,0°),(4,300°),
则点C的坐标表示为_______________.
(3,240°)
5. 如图Z3-3所示是某市区的部分平面示意图,为准确表示地理位置,可以建立平面直角坐标系用坐标表示地理位置.若交警大队的坐标是(5,3),中国银行的坐标是(4,1),则实验中学的坐标为____________.
(-2,1)
6.(1)写出如图Z3-4中点A,B,C,D,E,F的坐标;
(2)在图中描出下列各点:L(-5,-3),M(4,0),N(0,5),P(6,2).
解:(1)A(-2,-2),
B(-5,4),C(5,-4),
D(0,-3),E(2,5),
F(-3,0).
(2)略.
7. 已知:如图Z3-5,在△ABC中,AC=BC=5,AB=6,请以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,并求出△ABC的各顶点的坐标.
解:建立的直角坐标系如答图Z3-1.
过点C作CD⊥AB于点D,如答图Z3-1.
因为AC=BC=5,AB=6,
所以BD=AD= AB= ×6=3.
由勾股定理得CD= =4.
所以△ABC的各顶点坐标分别为A(0,0),
B(-6,0),C(-3,4).
1.点A(4,-2)关于x轴的对称点的坐标为( )
A.( 4,2 ) B.(-4,2)
C.(-4,-2) D.(-2,4)
2. (2020淮安)在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是( )
A. (2,3) B. (-3,2)
C. (-3,-2) D.(-2,-3)
专题2 轴对称与坐标变化
A
C
3. 如图Z3-6,将点A(-1,2)关于x轴作轴对称变换,则变换后点的坐标是( )
A.(1,2)
B.(1,-2)
C.(-1,-2)
D.(-2,-1)
C
4.已知△ABC在直角坐标系中的位置如图Z3-7,若△A′B′C′与△ABC关于y轴对称,则点A的对应点A′的坐标是( )
A.(-3,2) B.(3,2)
C.(-3,-2) D.(3,-2)
B
5. (2020达州)如图Z3-8,点P(-2,1)与点Q(a,b)关于直线l(y=-1)对称,则a+b=_________.
-5
6.如图Z3-9,已知在直角坐标系中,△OBC的顶点O(0,0),B(-6,0),且∠OCB=90°,OC=BC,则点C关于y轴的对称点C′的坐标是______________.
(3,3)
7. 在平面直角坐标系中,点M(a,b)与点N(3,-1)关于x轴对称,则a+b的值是_________.
8. 若点P(-2a,a-1)在y轴上,则点P的坐标为____________,点P关于x轴对称的点的坐标为____________.
4
(0,-1)
(0,1)
9.已知点P(a-1,-b+2)关于x轴的对称点为M,关于y轴的对称点为N,若点M与点N的坐标相同.
(1)求a,b的值;
(2)猜想点P的位置并说明理由.
解:(1)因为点P(a-1,-b+2)关于x轴的对称点为M,
所以M(a-1,b-2).
因为点P(a-1,-b+2)关于y轴的对称点为N,
所以N(-a+1,-b+2).
因为点M与点N的坐标相同,
所以a-1=-a+1,b-2=-b+2.
解得a=1,b=2.
(2)点P的位置是原点.理由如下.
因为a=1,b=2,
所以点P(a-1,-b+2)的坐标为(0,0),即点P为原点.
10.写出如图Z3-10中“小鱼”上所标各点的坐标并回答:
(1)点B,E的位置有什么特点?
(2)从点B与点E,点C与点D的位置看,它们的坐标有什么特点?
解:各点的坐标分别为A(-2,0),B(0,-2),
C(2,-1),D(2,1),E(0,2).
(1)点B(0,-2)和点E(0,2)关于x轴对称.
(2)点B(0,-2)与点E(0,2),点C(2,-1)
与点D(2,1),它们的横坐标相同,纵坐标互为
相反数.
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
