5.2 平行及其判定(3课时)
文档属性
| 名称 | 5.2 平行及其判定(3课时) |  | |
| 格式 | zip | ||
| 文件大小 | 422.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-20 21:55:25 | ||
图片预览








文档简介
课件52张PPT。人教版
七年级(下)数学教学课件5.2 平行线及其判定(第1课时)人教版七年级下册 日常生活中有哪些例子给你以不相交的形象? 请同学们想一想:很多国家的国旗上都有平行线古巴国旗俄罗斯国旗比利时国旗荷兰国旗阿根廷国旗瑞士国旗你喜欢滑雪吗?早在5000年前,人们就把滑雪作为雪上旅行的一种方式。滑雪运动最关键的是要保持
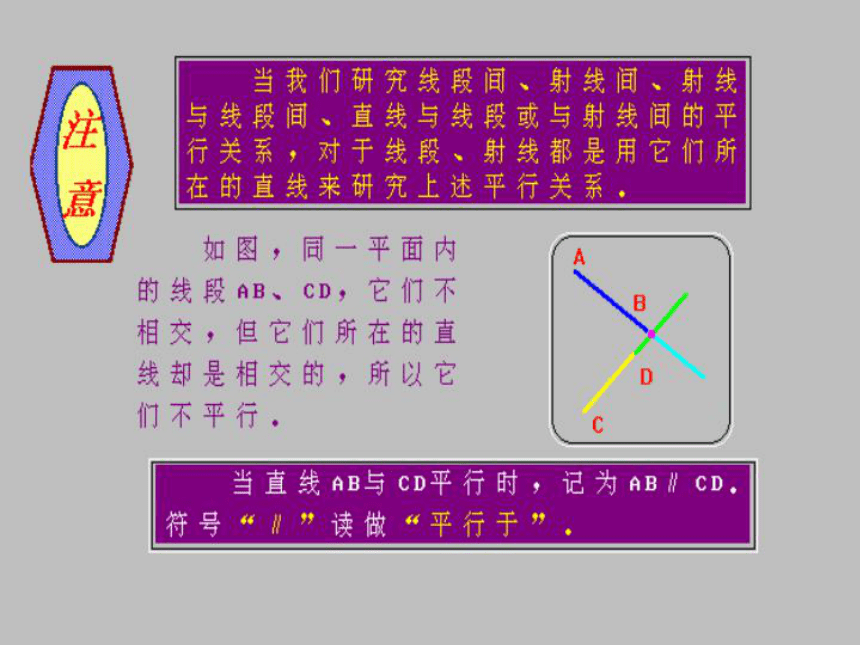
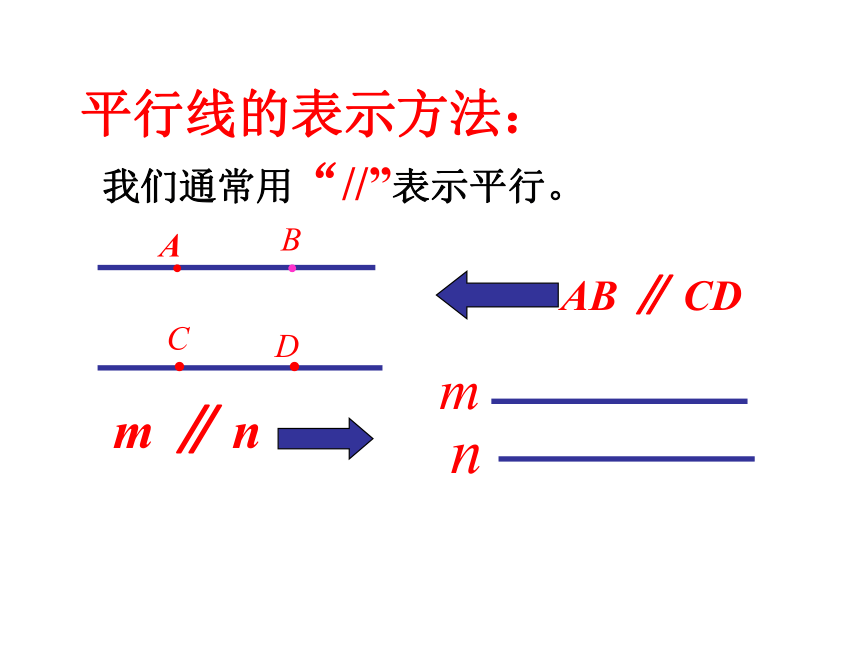
两只雪橇板的平行!我们通常用“//”表示平行。平行线的表示方法: 平面内的两条直线除平行外还有什么位置关系? 同一平面内的两条不重合的直线的位置关系只有两种:
相交或平行结论想一想如何画平行线?badc 平行公理:
经过直线外一点,有且只有一条直线
与这条直线平行.因为AB//EF,CD//EF
于是过点P就有两条直线
AB、CD都与EF平行.
根据平行公理,这是不可能的
也就是说,AB与CD不能相交,
只能平行.如图:三条直线AB、CD、EF。如果AB//EF ,CD//EF,
那么直线AB与CD可能相交吗?FEDCBA假设AB与CD相交,
设AB与CD相交于点P.平行公理:
经过直线外一点,有且只有一条直线
与这条直线平行.平行公理的推论:
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行. (1)经过点C能画出几条直线与直线AB平行? (2)过点D画一条直线与直线AB平行,它与(1)中所画的直线平行吗? ①经过直线外一点,有且只有一条直线与这条直线平行。 ②如果两条直线都与第三条直线平行,那么这两条直线互相平行。···ABCD·B结论练一练 本节课你的收获是什么?(1)什么是平行线; (3)平行线的画法; (2)平行线的表示方法;(4)平行线的两个公理。(5)在同一平面内两条直线有几种位置关系?小结5.2 平行线及其判定
(第2课时)人教版七年级下册一、知识回顾1、直线的位置关系有哪几种?2、怎样画两条平行的直线?从画图过程,三角板起到什么作用?要判断直线a //b,你有办法了吗?两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:
同位角相等,两直线平行。 ∵ ∠1=∠2(已知)∴ a∥b(同位角相等,两直线平行)如图:条件:1,同位角. 2, 相等.
结论: 两条构成同位角的被截的直线平行.大家来探索!① 如图: 如果∠1=∠2,
那么a与b平行吗?内错角相等,两直线平行。12条件:1. 内错角. 2. 相等.
结论: 两条构成内错角的被截的直线平行.② 如图:
如果∠1+∠2=180o,
那么a与b平行吗?同旁内角互补,两直线平行。大家来探索!条件:1,同旁内角. 2, 互补.
结论: 两条构成同旁内角的被截的直线平行.同位角相等,两直线平行。同旁内角互补,两直线平行。内错角相等,两直线平行。直线平行的条件例1① ∵ ∠2 =___(已知)
∴ ___∥___( )② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )③∵ ∠4 +___=180o(已知)
∴ ___∥___( )∠6ABCDABCD∠5ABCDAC14235867BD同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行平行线的判定例2① ∵ ∠1 =_____(已知)
∴ AB∥CE( )② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF( )③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )ABCE∠2④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )平行线的判定∠3∠313542CFEADB内错角相等,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行例3如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?平行线的判定AC1423BD5已知∠3=45 °,∠1与∠2互余,试说明 ? 解:由于∠1与∠2是对顶角,
∴∠1=∠2
又∵∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)看谁是高手AB//CD同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图判定数量关系位置关系小结5.2 平行线及其判定
(第3课时)人教版七年级下册回顾:如何判断两条直线平行?两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行。同位角:同旁同侧内错角:内部两旁同旁内角:内部同旁BD21E已知∠1= ∠2,
你能得出AB ∥CD吗?ACFOP因为 ∠1=∠2所以 ∠2=∠3 ∠1=∠3(对顶角相等)(等量代换)从而AB∥CD. (同位角相等,两直线平行)∠1和∠2是内错角 思考1答: AB ∥CD,理由如下:BD21E判断直线平行方法2ACFOP两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行。右图中,如果∠1+∠2=180°,
能否得出AB∥CD?思考2BD21EACFOP∠1和∠2是同旁内角 因为 ∠1+∠2=180°所以 ∠2=∠3 ∠1+∠3=180°(邻补角的定义)(同角的补角相等)从而AB∥CD. (同位角相等,两直线平行)你还有其他
方法吗?答:AB ∥CD,理由如下:右图中,如果∠1+∠2=180°,
能得出AB∥CD吗?BD21EACFOP∠1和∠2是同旁内角 因为 ∠1+∠2=180°所以 ∠2=∠3 ∠1+∠3=180°(邻补角的定义)(同角的补角相等)从而AB∥CD. (内错角相等,两直线平行)理由:判断直线平行方法3两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行。BD21EACFOP
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。练一练ba内错角相等,两直线平行同位角相等,两直线平行3cd42cd31ab同旁内角互补,两直线平行1.如图从∠1=∠4,可以推出 ∥ ,
理由是 。(3)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。(2)从∠ =∠ ,可以推出AD∥BC,
理由是 。(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。练一练AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行23内错角相等,两直线平行ABC同位角相等,两直线平行2.如图3.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?答:垂直于同一条直线的两条直线平行.练一练因为 b⊥a所以 ∠2=90° (垂直的定义)从而b∥c. (同位角相等,两直线平行)所以 ∠1=90° (垂直的定义)因为 c ⊥a所以 ∠1=∠2(等量代换)解法1:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12解法2:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)abc12解法3:结论如果两条直线都垂直于同一条直线,
那么这两条直线平行。bca有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?试一试12方案1:45° 45° 45°1245°方案2:135° 45°方案3:收获通过这节课的学习,
你有哪些收获?议一议1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.判定两条直线是否平行的方法有:小结
七年级(下)数学教学课件5.2 平行线及其判定(第1课时)人教版七年级下册 日常生活中有哪些例子给你以不相交的形象? 请同学们想一想:很多国家的国旗上都有平行线古巴国旗俄罗斯国旗比利时国旗荷兰国旗阿根廷国旗瑞士国旗你喜欢滑雪吗?早在5000年前,人们就把滑雪作为雪上旅行的一种方式。滑雪运动最关键的是要保持
两只雪橇板的平行!我们通常用“//”表示平行。平行线的表示方法: 平面内的两条直线除平行外还有什么位置关系? 同一平面内的两条不重合的直线的位置关系只有两种:
相交或平行结论想一想如何画平行线?badc 平行公理:
经过直线外一点,有且只有一条直线
与这条直线平行.因为AB//EF,CD//EF
于是过点P就有两条直线
AB、CD都与EF平行.
根据平行公理,这是不可能的
也就是说,AB与CD不能相交,
只能平行.如图:三条直线AB、CD、EF。如果AB//EF ,CD//EF,
那么直线AB与CD可能相交吗?FEDCBA假设AB与CD相交,
设AB与CD相交于点P.平行公理:
经过直线外一点,有且只有一条直线
与这条直线平行.平行公理的推论:
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行. (1)经过点C能画出几条直线与直线AB平行? (2)过点D画一条直线与直线AB平行,它与(1)中所画的直线平行吗? ①经过直线外一点,有且只有一条直线与这条直线平行。 ②如果两条直线都与第三条直线平行,那么这两条直线互相平行。···ABCD·B结论练一练 本节课你的收获是什么?(1)什么是平行线; (3)平行线的画法; (2)平行线的表示方法;(4)平行线的两个公理。(5)在同一平面内两条直线有几种位置关系?小结5.2 平行线及其判定
(第2课时)人教版七年级下册一、知识回顾1、直线的位置关系有哪几种?2、怎样画两条平行的直线?从画图过程,三角板起到什么作用?要判断直线a //b,你有办法了吗?两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:
同位角相等,两直线平行。 ∵ ∠1=∠2(已知)∴ a∥b(同位角相等,两直线平行)如图:条件:1,同位角. 2, 相等.
结论: 两条构成同位角的被截的直线平行.大家来探索!① 如图: 如果∠1=∠2,
那么a与b平行吗?内错角相等,两直线平行。12条件:1. 内错角. 2. 相等.
结论: 两条构成内错角的被截的直线平行.② 如图:
如果∠1+∠2=180o,
那么a与b平行吗?同旁内角互补,两直线平行。大家来探索!条件:1,同旁内角. 2, 互补.
结论: 两条构成同旁内角的被截的直线平行.同位角相等,两直线平行。同旁内角互补,两直线平行。内错角相等,两直线平行。直线平行的条件例1① ∵ ∠2 =___(已知)
∴ ___∥___( )② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )③∵ ∠4 +___=180o(已知)
∴ ___∥___( )∠6ABCDABCD∠5ABCDAC14235867BD同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行平行线的判定例2① ∵ ∠1 =_____(已知)
∴ AB∥CE( )② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF( )③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )ABCE∠2④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )平行线的判定∠3∠313542CFEADB内错角相等,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行例3如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?平行线的判定AC1423BD5已知∠3=45 °,∠1与∠2互余,试说明 ? 解:由于∠1与∠2是对顶角,
∴∠1=∠2
又∵∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)看谁是高手AB//CD同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图判定数量关系位置关系小结5.2 平行线及其判定
(第3课时)人教版七年级下册回顾:如何判断两条直线平行?两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行。同位角:同旁同侧内错角:内部两旁同旁内角:内部同旁BD21E已知∠1= ∠2,
你能得出AB ∥CD吗?ACFOP因为 ∠1=∠2所以 ∠2=∠3 ∠1=∠3(对顶角相等)(等量代换)从而AB∥CD. (同位角相等,两直线平行)∠1和∠2是内错角 思考1答: AB ∥CD,理由如下:BD21E判断直线平行方法2ACFOP两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行。右图中,如果∠1+∠2=180°,
能否得出AB∥CD?思考2BD21EACFOP∠1和∠2是同旁内角 因为 ∠1+∠2=180°所以 ∠2=∠3 ∠1+∠3=180°(邻补角的定义)(同角的补角相等)从而AB∥CD. (同位角相等,两直线平行)你还有其他
方法吗?答:AB ∥CD,理由如下:右图中,如果∠1+∠2=180°,
能得出AB∥CD吗?BD21EACFOP∠1和∠2是同旁内角 因为 ∠1+∠2=180°所以 ∠2=∠3 ∠1+∠3=180°(邻补角的定义)(同角的补角相等)从而AB∥CD. (内错角相等,两直线平行)理由:判断直线平行方法3两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行。BD21EACFOP
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。练一练ba内错角相等,两直线平行同位角相等,两直线平行3cd42cd31ab同旁内角互补,两直线平行1.如图从∠1=∠4,可以推出 ∥ ,
理由是 。(3)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。(2)从∠ =∠ ,可以推出AD∥BC,
理由是 。(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。练一练AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行23内错角相等,两直线平行ABC同位角相等,两直线平行2.如图3.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?答:垂直于同一条直线的两条直线平行.练一练因为 b⊥a所以 ∠2=90° (垂直的定义)从而b∥c. (同位角相等,两直线平行)所以 ∠1=90° (垂直的定义)因为 c ⊥a所以 ∠1=∠2(等量代换)解法1:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12解法2:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)abc12解法3:结论如果两条直线都垂直于同一条直线,
那么这两条直线平行。bca有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?试一试12方案1:45° 45° 45°1245°方案2:135° 45°方案3:收获通过这节课的学习,
你有哪些收获?议一议1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.判定两条直线是否平行的方法有:小结
