【核心素养目标】24.2.2 直线和圆的位置关系(2) 导学案
文档属性
| 名称 | 【核心素养目标】24.2.2 直线和圆的位置关系(2) 导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 21:54:29 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.2.2 直线和圆的位置关系(2)导学案
课题 24.2.2 直线和圆的位置关系(2) 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 直线和圆相切是直线和圆的位置关系中的一种特殊并且重要的位置关系,圆的切线是连接直线与曲线的重要桥梁,是研究三角形内切圆、切线长定理和正多边形与圆的关系的基础.
核心素养分析 切线的判定定理与性质定理揭示了直线和圆的半径的特殊位置,即过半径外端并与这条半径垂直,两个定理互为逆命题, 切线的判定定理的探究过程体现了由一般到特殊的研究方法。突出图形性质的探索过程,培养几何直观操作和逻辑推理等核心素养.
学习目标 1.能判定一条直线是否为圆的切线,会过圆上一点画圆的切线.2.理解切线的判定定理和性质定理,会用这两个定理解决简单问题.3.经历观察、实验、猜想、证明等数学活动过程,发展合情推理能力和初步演绎推理能力.
重点 理解并掌握切线的性质和判定方法.
难点 应用切线的性质和判定方法解决问题.
教学过程
课前预学 引入思考问题1:下雨天,转动的雨伞上的水滴是顺着伞的什么方向飞出去的 问题2:砂轮转动时,火花是沿着砂轮的什么方向飞出去的 都是沿着圆的切线的方向飞出的. 1、切线的判定定理思考:1.如图,直线 l 和⊙O有什么位置关系 2.如图,在⊙O中经过半径OA的外端点A作直线l⊥OA,则圆心O到直线 l 的距离是多少?进一步思考:已知圆O上一点A,怎样根据圆的切线定义过点A作圆O的切线?观察:(1) 圆心O到直线AB的距离和圆的半径有什么数量关系 (2)二者位置有什么关系?为什么? ●切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.几何语言: 探索切线的性质定理.思考:将上面“思考”中的问题反过来,如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢?你有什么方法证明。●归纳:切线性质 圆的切线垂直于经过切点的半径. 几何符号表达:
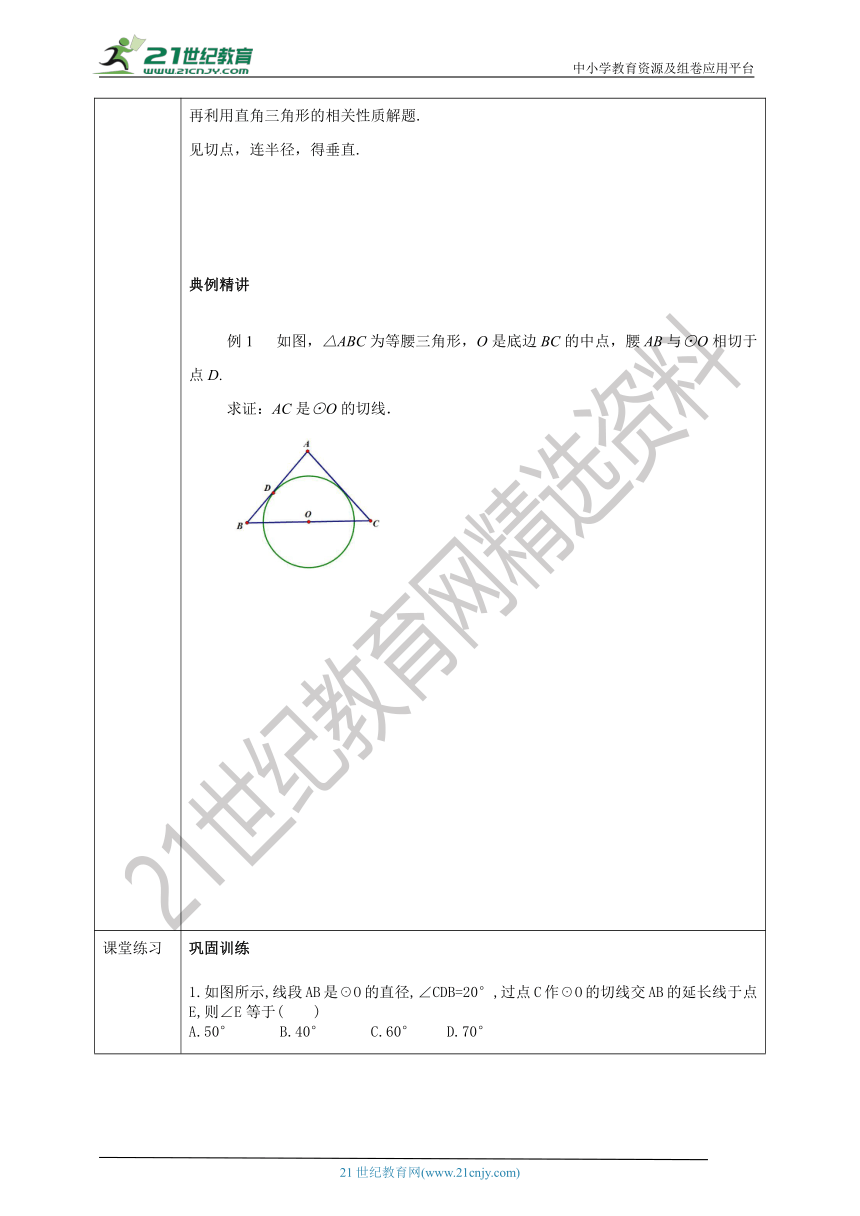
新知讲解 提炼概念方法总结:①、当已知直线过圆上的一点时,连接圆心和该点得到圆的半径,然后 ,即可得出已知直线为圆的切线.有交点,连半径,证垂直;②、当未提及直线与圆有公共点时,过圆心作直线的垂线,证明 ,即可得出已知直线为圆的切线.无交点,作垂直,证半径. 利用切线的性质解题时,常需连接辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.见切点,连半径,得垂直.典例精讲 例1 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D. 求证:AC是⊙O的切线.
课堂练习 巩固训练 1.如图所示,线段AB是☉O的直径,∠CDB=20°,过点C作☉O的切线交AB的延长线于点E,则∠E等于( )A.50° B.40° C.60° D.70°2.如图,已知△ABC内接于☉O,BC是☉O的直径,MN与☉O相切,切点为A,若∠MAB=30°.则∠B=________.3.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E. 求证:PE是⊙O的切线.4.在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于D,以D为圆心,DB长为半径作⊙D.求证: AC是⊙D的切线.5.如图,P是☉O外一点,PA切☉O于点A,AB是☉O的直径,BC∥OP且交☉O于点C,请准确判断直线PC与☉O是怎样的位置关系,并说明理由.6.如图,已知AB是☉O的直径,P为☉O外一点,且AP∥BC,∠P=∠BAC.(1)求证:PA为☉O的切线.(2)若OB=5,OP= ,求AC的长. 答案引入思考思考: 在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是多少?直线l和⊙O有什么位置关系?可以看出,圆心O到直线l的距离是⊙O的半径,直线l就是⊙O的切线.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.几何语言: ∵OA⊥l ∴l是⊙O的切线环节三:探究切线的性质定理思考:如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直?证明:(1)假设AB与CD不垂直,过点O作一条直径垂直于CD于M,(2)则OM<OA,即圆心到直线CD的距离小于⊙O的半径,因此,CD与⊙O相交. 这与已知条件“直线与⊙O相切”相矛盾.(3)所以AB与CD垂直.切线的性质定理:圆的切线垂直于过切点的半径.几何语言: ∵l是⊙O的切线 ∴OA⊥l提炼概念 典例精讲 例证明:连接OD、OA,过O作OE⊥AC.∵⊙O与AB相切于D,∴OD⊥AB.又∵△ABC为等腰三角形,O是底边BC的中点.∴AO平分∠BAC,∴OE=OD.∴OE是⊙O半径,∴AC是⊙O的切线.小结:证切线时辅助线的添加方法有切点,连半径,证垂直;无交点,作垂直,证半径.巩固训练1.A2.60°3.证明:连接OP. ∵AB=AC,∴∠B=∠C. ∵OB=OP,∴∠B=∠OPB, ∴∠OPB=∠C. ∴OP∥AC. ∵PE⊥AC, ∴PE⊥OP. ∴PE为⊙O的切线.4.证明:AC是⊙O的切线 。理由如下:过点D作DE⊥AC,垂足为E∵∠B=90° ∴BD⊥AB又∵DE⊥ACAD平分∠BAC∴DE=BD∴直线AC是⊙O的切线.5.解:PC与☉O相切.连接OC,则OC=OB,∴∠B=∠OCB.∵BC∥OP,∴∠B=∠AOP,∠OCB=∠COP,∴∠AOP=∠COP.在△AOP与△COP中,OA=OC,∠AOP=∠COP,OP=OP,∴△AOP≌△COP.又∵PA是☉O的切线,∴∠OCP=∠OAP=90°.又∵OC是半径,∴PC是☉O的切线.6.解:(1)设AC与OP相交于点H.∵AB是径,∴AC⊥BC,∠BAC+∠B=90°.∵OP∥BC,∴OP⊥AC,∠AOP=∠B.∵∠P=∠BAC,∴∠P+∠AOP=90°,于是∠OAP=90°,∴PA为☉O的切线.(2)∵OP⊥AC,∴AC=2AH, 在直角三角形PAO中,由面积法可知:AH=4∴AC=2AH=8.
课堂小结 直线和圆的位置关系
C
D
B
O
A
定义法
数量法
判定定理
判定定理
性质定理
性质定理和判定定理的综合应用
性质定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
24.2.2 直线和圆的位置关系(2)导学案
课题 24.2.2 直线和圆的位置关系(2) 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 直线和圆相切是直线和圆的位置关系中的一种特殊并且重要的位置关系,圆的切线是连接直线与曲线的重要桥梁,是研究三角形内切圆、切线长定理和正多边形与圆的关系的基础.
核心素养分析 切线的判定定理与性质定理揭示了直线和圆的半径的特殊位置,即过半径外端并与这条半径垂直,两个定理互为逆命题, 切线的判定定理的探究过程体现了由一般到特殊的研究方法。突出图形性质的探索过程,培养几何直观操作和逻辑推理等核心素养.
学习目标 1.能判定一条直线是否为圆的切线,会过圆上一点画圆的切线.2.理解切线的判定定理和性质定理,会用这两个定理解决简单问题.3.经历观察、实验、猜想、证明等数学活动过程,发展合情推理能力和初步演绎推理能力.
重点 理解并掌握切线的性质和判定方法.
难点 应用切线的性质和判定方法解决问题.
教学过程
课前预学 引入思考问题1:下雨天,转动的雨伞上的水滴是顺着伞的什么方向飞出去的 问题2:砂轮转动时,火花是沿着砂轮的什么方向飞出去的 都是沿着圆的切线的方向飞出的. 1、切线的判定定理思考:1.如图,直线 l 和⊙O有什么位置关系 2.如图,在⊙O中经过半径OA的外端点A作直线l⊥OA,则圆心O到直线 l 的距离是多少?进一步思考:已知圆O上一点A,怎样根据圆的切线定义过点A作圆O的切线?观察:(1) 圆心O到直线AB的距离和圆的半径有什么数量关系 (2)二者位置有什么关系?为什么? ●切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.几何语言: 探索切线的性质定理.思考:将上面“思考”中的问题反过来,如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢?你有什么方法证明。●归纳:切线性质 圆的切线垂直于经过切点的半径. 几何符号表达:
新知讲解 提炼概念方法总结:①、当已知直线过圆上的一点时,连接圆心和该点得到圆的半径,然后 ,即可得出已知直线为圆的切线.有交点,连半径,证垂直;②、当未提及直线与圆有公共点时,过圆心作直线的垂线,证明 ,即可得出已知直线为圆的切线.无交点,作垂直,证半径. 利用切线的性质解题时,常需连接辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.见切点,连半径,得垂直.典例精讲 例1 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D. 求证:AC是⊙O的切线.
课堂练习 巩固训练 1.如图所示,线段AB是☉O的直径,∠CDB=20°,过点C作☉O的切线交AB的延长线于点E,则∠E等于( )A.50° B.40° C.60° D.70°2.如图,已知△ABC内接于☉O,BC是☉O的直径,MN与☉O相切,切点为A,若∠MAB=30°.则∠B=________.3.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E. 求证:PE是⊙O的切线.4.在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于D,以D为圆心,DB长为半径作⊙D.求证: AC是⊙D的切线.5.如图,P是☉O外一点,PA切☉O于点A,AB是☉O的直径,BC∥OP且交☉O于点C,请准确判断直线PC与☉O是怎样的位置关系,并说明理由.6.如图,已知AB是☉O的直径,P为☉O外一点,且AP∥BC,∠P=∠BAC.(1)求证:PA为☉O的切线.(2)若OB=5,OP= ,求AC的长. 答案引入思考思考: 在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是多少?直线l和⊙O有什么位置关系?可以看出,圆心O到直线l的距离是⊙O的半径,直线l就是⊙O的切线.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.几何语言: ∵OA⊥l ∴l是⊙O的切线环节三:探究切线的性质定理思考:如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直?证明:(1)假设AB与CD不垂直,过点O作一条直径垂直于CD于M,(2)则OM<OA,即圆心到直线CD的距离小于⊙O的半径,因此,CD与⊙O相交. 这与已知条件“直线与⊙O相切”相矛盾.(3)所以AB与CD垂直.切线的性质定理:圆的切线垂直于过切点的半径.几何语言: ∵l是⊙O的切线 ∴OA⊥l提炼概念 典例精讲 例证明:连接OD、OA,过O作OE⊥AC.∵⊙O与AB相切于D,∴OD⊥AB.又∵△ABC为等腰三角形,O是底边BC的中点.∴AO平分∠BAC,∴OE=OD.∴OE是⊙O半径,∴AC是⊙O的切线.小结:证切线时辅助线的添加方法有切点,连半径,证垂直;无交点,作垂直,证半径.巩固训练1.A2.60°3.证明:连接OP. ∵AB=AC,∴∠B=∠C. ∵OB=OP,∴∠B=∠OPB, ∴∠OPB=∠C. ∴OP∥AC. ∵PE⊥AC, ∴PE⊥OP. ∴PE为⊙O的切线.4.证明:AC是⊙O的切线 。理由如下:过点D作DE⊥AC,垂足为E∵∠B=90° ∴BD⊥AB又∵DE⊥ACAD平分∠BAC∴DE=BD∴直线AC是⊙O的切线.5.解:PC与☉O相切.连接OC,则OC=OB,∴∠B=∠OCB.∵BC∥OP,∴∠B=∠AOP,∠OCB=∠COP,∴∠AOP=∠COP.在△AOP与△COP中,OA=OC,∠AOP=∠COP,OP=OP,∴△AOP≌△COP.又∵PA是☉O的切线,∴∠OCP=∠OAP=90°.又∵OC是半径,∴PC是☉O的切线.6.解:(1)设AC与OP相交于点H.∵AB是径,∴AC⊥BC,∠BAC+∠B=90°.∵OP∥BC,∴OP⊥AC,∠AOP=∠B.∵∠P=∠BAC,∴∠P+∠AOP=90°,于是∠OAP=90°,∴PA为☉O的切线.(2)∵OP⊥AC,∴AC=2AH, 在直角三角形PAO中,由面积法可知:AH=4∴AC=2AH=8.
课堂小结 直线和圆的位置关系
C
D
B
O
A
定义法
数量法
判定定理
判定定理
性质定理
性质定理和判定定理的综合应用
性质定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
