鲁教版(五四制)数学七年级下册 7.4 二元一次方程与一次函数(1) 课件(共14张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级下册 7.4 二元一次方程与一次函数(1) 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 404.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-17 08:46:55 | ||
图片预览






文档简介
(共14张PPT)
二元一次方程与一次函数
学习目标:
1、初步体会二元一次方程(组)与一次函数的关系;
2、能从“图形”的角度看待二元一次方程和二元一次方程组;
3、会利用待定系数法确定一次函数表达式。
问题一
如果将解中的x,y的值分别作为点的横、纵坐标,在平面直角坐标系中描出这些点,你有什么发现?与以前学过的什么知识有关系?
要求:1、从刚才举出的几个二元一次方程中任选一个研究
2、小组成员分工协作完成
练习1:若方程 有一个解为 ,则一次函
数 的图像上必有一点为___________。
跟踪练习
练习2:一次函数 的图象上有一点坐标为(3,2),
则方程 必有一个解为__________。
(2,1)
问题二
要求:任选其中一个方程组求解,先独立思考,
再小组合作交流讨论。
如果将刚才的方程组随机组合得到一些方程组,你有什么新的方法解这些方程组吗?
问题二
“数”“形”结合
一般地,从“图形”的角度看,确定两条直线交点的坐标,相当于求相映的二元一次方程组的解;解一个二元一次方程组,相当于确定两条直线交点的坐标。
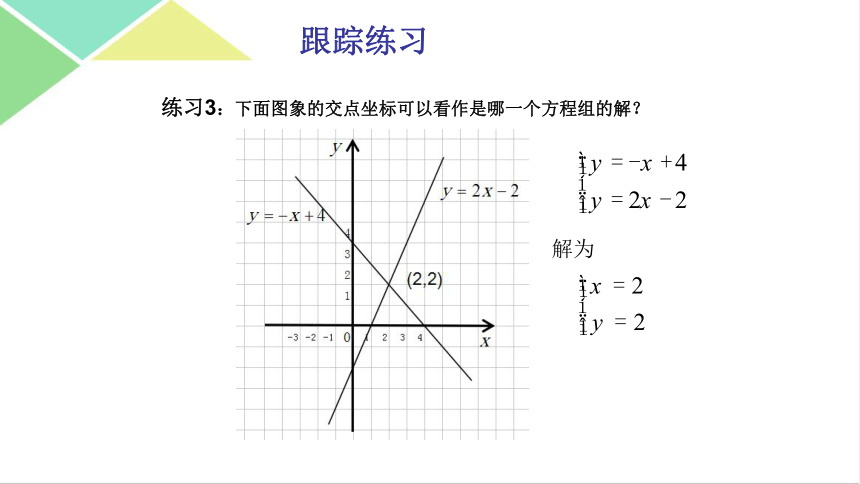
练习3:下面图象的交点坐标可以看作是哪一个方程组的解?
跟踪练习
解为
练习4:若二元一次方程组 的解为 ,
则一次函数 的图像与函数 的交点坐标
为_______。
跟踪练习
(2,2)
例题讲解
例:利用一次函数图象解二元一次方程组
解:
变形为
变形为
0
2
0
4
0
-3
0
(2,1)
原方程组的解为
练习5:用图象法解二元一次方程组
跟踪练习
利用图象法求出的是二元一次
方程组的近似解。
问题三
一般的二元一次方程组有解吗?如果有解,那么有几个解呢?如果无解,你能举个例子吗?
要求:小组合作探究
直线
直线
有一个交点
方程组有一个解
图象
直线
直线
没有交点
方程组无解
图象
五、合作总结
1、图象法求二元一次方程组解的特点
2、二元一次方程组解的情况
一解
无解
1、初步体会二元一次方程(组)与一次函数的关系;
2、能从“图形”的角度看待二元一次方程和二元一次方程组;
3、会利用待定系数法确定一次函数表达式。
学习目标:
其他收获:
二元一次方程与一次函数
学习目标:
1、初步体会二元一次方程(组)与一次函数的关系;
2、能从“图形”的角度看待二元一次方程和二元一次方程组;
3、会利用待定系数法确定一次函数表达式。
问题一
如果将解中的x,y的值分别作为点的横、纵坐标,在平面直角坐标系中描出这些点,你有什么发现?与以前学过的什么知识有关系?
要求:1、从刚才举出的几个二元一次方程中任选一个研究
2、小组成员分工协作完成
练习1:若方程 有一个解为 ,则一次函
数 的图像上必有一点为___________。
跟踪练习
练习2:一次函数 的图象上有一点坐标为(3,2),
则方程 必有一个解为__________。
(2,1)
问题二
要求:任选其中一个方程组求解,先独立思考,
再小组合作交流讨论。
如果将刚才的方程组随机组合得到一些方程组,你有什么新的方法解这些方程组吗?
问题二
“数”“形”结合
一般地,从“图形”的角度看,确定两条直线交点的坐标,相当于求相映的二元一次方程组的解;解一个二元一次方程组,相当于确定两条直线交点的坐标。
练习3:下面图象的交点坐标可以看作是哪一个方程组的解?
跟踪练习
解为
练习4:若二元一次方程组 的解为 ,
则一次函数 的图像与函数 的交点坐标
为_______。
跟踪练习
(2,2)
例题讲解
例:利用一次函数图象解二元一次方程组
解:
变形为
变形为
0
2
0
4
0
-3
0
(2,1)
原方程组的解为
练习5:用图象法解二元一次方程组
跟踪练习
利用图象法求出的是二元一次
方程组的近似解。
问题三
一般的二元一次方程组有解吗?如果有解,那么有几个解呢?如果无解,你能举个例子吗?
要求:小组合作探究
直线
直线
有一个交点
方程组有一个解
图象
直线
直线
没有交点
方程组无解
图象
五、合作总结
1、图象法求二元一次方程组解的特点
2、二元一次方程组解的情况
一解
无解
1、初步体会二元一次方程(组)与一次函数的关系;
2、能从“图形”的角度看待二元一次方程和二元一次方程组;
3、会利用待定系数法确定一次函数表达式。
学习目标:
其他收获:
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
