2.5三角函数的应用 同步练习(含答案)
文档属性
| 名称 | 2.5三角函数的应用 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-16 08:00:15 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
5 三角函数的应用
基础过关
知识点1 三角函数的应用——仰角、俯角问题
1.如图,在C处测得旗杆AB的顶端A的仰角为30°,向旗杆前进10米到达D处,在D处测得A的仰角为60°,则旗杆的高为( )
米 B.10米 米 米
2.某高铁线路规划中,需要确定河流的宽度AB的长.已知在离地面600 m高度C处的无人机上,测得正前方A,B两点处的俯角分别为60°和45°,则河流的宽度AB的长为多
少米 (结果保留根号)
3.在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是53°,从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°,综合楼高24米.请你帮小明求出办公楼的高度.(结果精确到0.1,参考数据:
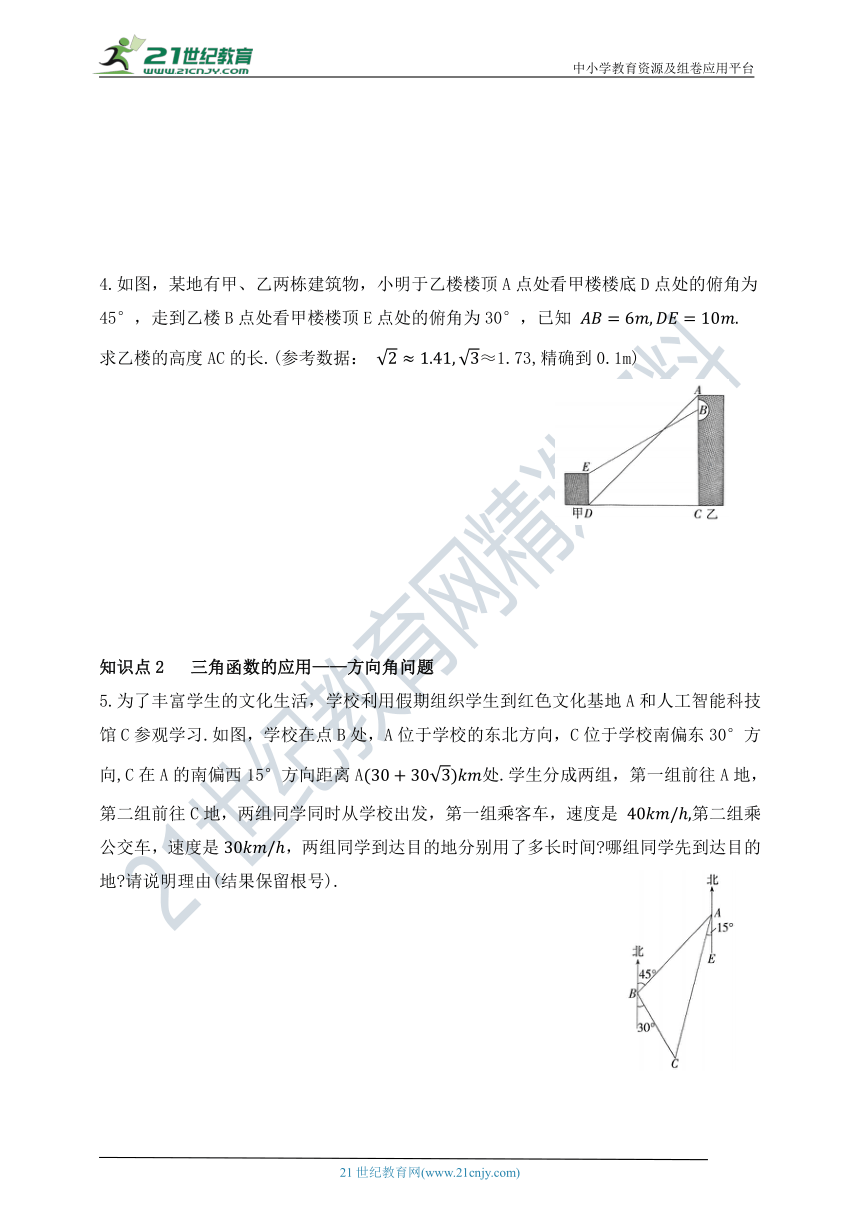
4.如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为30°,已知
求乙楼的高度AC的长.(参考数据: ≈1.73,精确到0.1m)
知识点2 三角函数的应用——方向角问题
5.为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习.如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向距离A处.学生分成两组,第一组前往A地,
第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是 第二组乘公交车,速度是,两组同学到达目的地分别用了多长时间 哪组同学先到达目的地 请说明理由(结果保留根号).
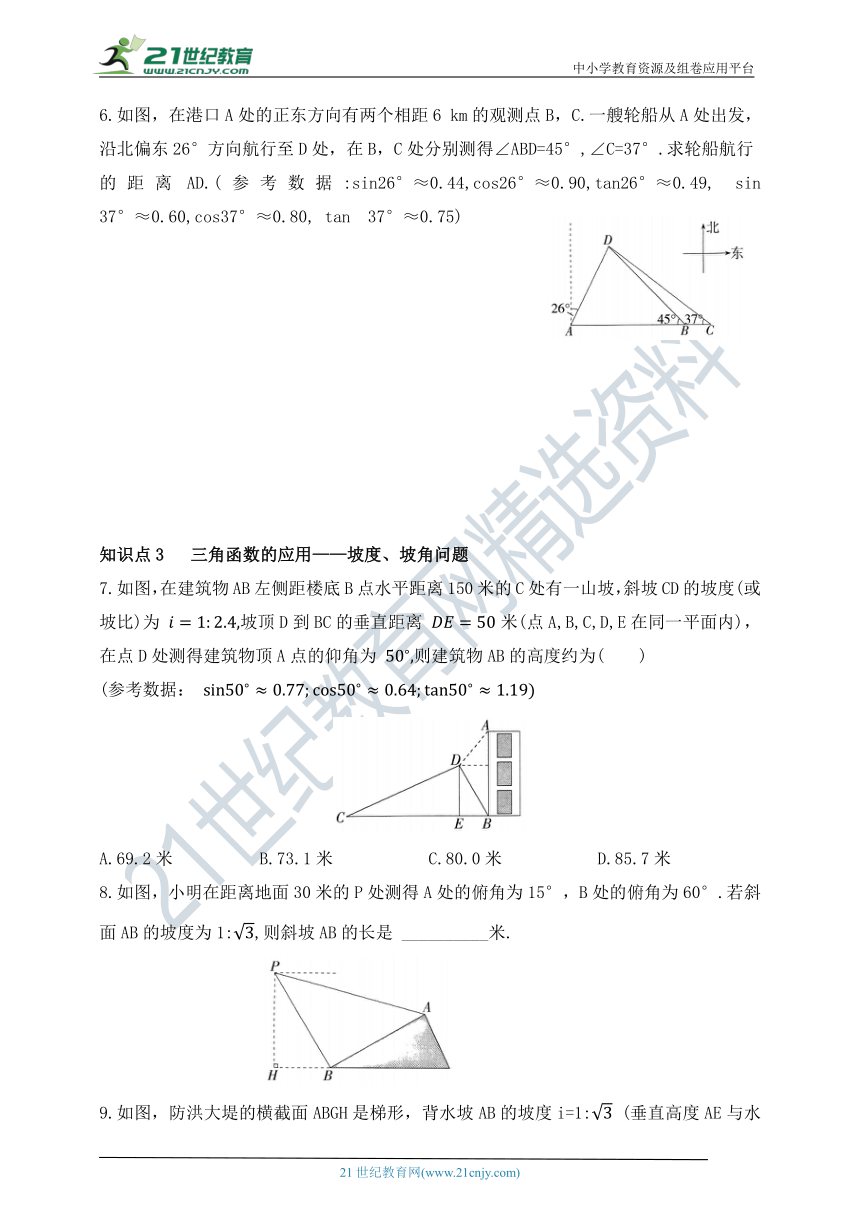
6.如图,在港口A处的正东方向有两个相距6 km的观测点B,C.一艘轮船从A处出发,沿北偏东26°方向航行至D处,在B,C处分别测得∠ABD=45°,∠C=37°.求轮船航行
的距离AD.(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49, sin 37°≈0.60,cos37°≈0.80, tan 37°≈0.75)
知识点3 三角函数的应用——坡度、坡角问题
7.如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为 坡顶D到BC的垂直距离 米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为 则建筑物AB的高度约为( )
(参考数据:
A.69.2米 B.73.1米 C.80.0米 D.85.7米
8.如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面AB的坡度为1:,则斜坡AB的长是 __________米.
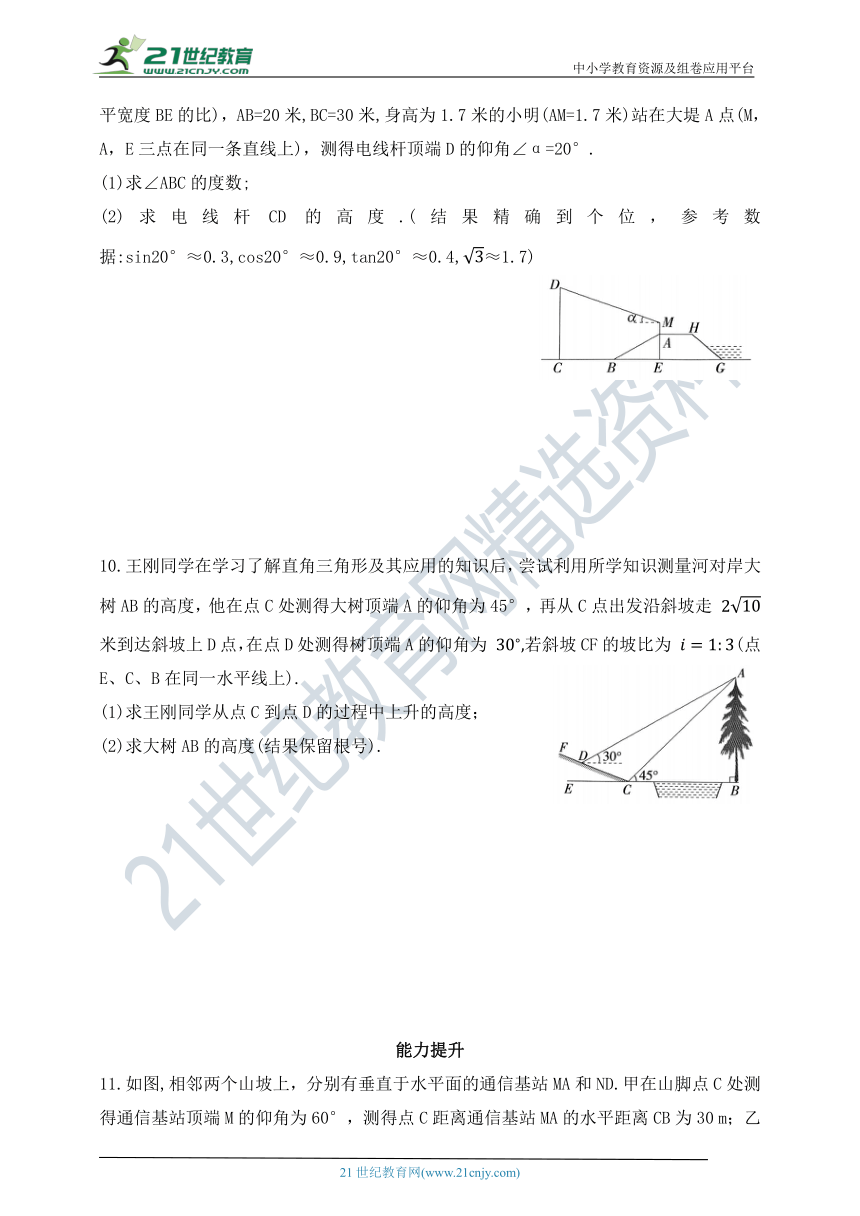
9.如图,防洪大堤的横截面ABGH是梯形,背水坡AB的坡度i=1: (垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠α=20°.
(1)求∠ABC的度数;
(2)求电线杆CD的高度.(结果精确到个位,参考数据:sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,≈1.7)
10.王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走 米到达斜坡上D点,在点D处测得树顶端A的仰角为 若斜坡CF的坡比为 (点E、C、B在同一水平线上).
(1)求王刚同学从点C到点D的过程中上升的高度;
(2)求大树AB的高度(结果保留根号).
能力提升
11.如图,相邻两个山坡上,分别有垂直于水平面的通信基站MA和ND.甲在山脚点C处测得通信基站顶端M的仰角为60°,测得点C距离通信基站MA的水平距离CB为30 m;乙在另一座山脚点F处测得点F距离通信基站ND的水平距离FE为50 m,测得山坡DF的坡度i=1:1.25.若 DE,点C,B,E,F在同一水平线上,则两个通信基站顶端M与顶端N的高度差为(参考数据: ( )
A.9.0 m B.12.8 m C.13.1 m D.22.7 m
12.如图,建筑物BC上有一旗杆AB,从与BC相距20 m的D处观测旗杆顶部A的仰角为52°,观测旗杆底部B的仰角为45°,求旗杆AB的高度(结果保留到小数点后一位.参考数据:
13.如图,在小山的东侧A庄有一热气球,由于受西风的影响,以每分钟35m的速度沿着与水平方向成角的方向飞行,40 min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为 求A庄与B庄的距离及山高(参考数据: 结果精确到个位).
14.小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向,C在北偏东 方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.
(1)求 的度数;
(2)求两棵银杏树B,C之间的距离(结果保留根号).
15.[数学建模]因东坡文化远近闻名的遗爱湖公园,“国庆黄金周”期间,游人络绎不绝,现有一艘游船载着游客在遗爱湖中游览,如图,当船在A处时,船上游客发现岸上 处的临皋亭和处的遗爱亭都在东北方向;当游船向正东方向行驶600m到达B处时,游客发现遗爱亭在北偏西 方向;当游船继续向正东方向行驶400 m到达C处时,游客发现临皋亭在北偏西 方向.
(1)求A处到临皋亭 处的距离;
(2)求临皋亭P 处与遗爱亭 处之间的距离.(计算结果保留根号)
参考答案
基础过关
1.C 由题意得∠C=30°,∠ADB=60°,∴∠DAC=∠ADB-∠C=30°.∴∠DAC=∠C.
∴AD=DC=10米.在Rt△ADB中, (米).故选C.
2.解析 由题意得∠COA=90°,∠CAO=60°,∠CBO=600 m.∴
3.解析 在Rt△ABD中,AB=24米,∠BDA=53°,∠BAD=90°,∴
在Rt△ACD中,∠CDA=90°,∠CAD=30°,∴(米).故办公楼的高度约为10.4米.
4.解析 过点E作EFLAC于F,则四边形CDEF为矩形.
∴EF=CD,CF=DE=10m.易知∠EBF=60°,∠DAC=45°,
设AC=x m,则CD=EF=x m,BF=(x-16)m,
在Rt△BEF中,∠EBF=60°,, ∴
答:乙楼的高度AC的长约为37.8m.
5.解析 如图,过点B作BD⊥AC于D.
由题意得,∠BAE=45°,∠ABC=180°-45°-30°=105°.
又∠CAE=15°,∴∠BAC=30°,∴∠ACB=45°.设BD=x km.
在Rt△BCD中,∠DCB=45°=∠CBD,∴CD=BD=x km,BC=
在Rt△BDA中,
解得
第一组用时:
第二组用时:
∴第二组先到达目的地.
6.解析 如图,过点D作 于点H.
在 中, 在Rt△DBH中, ∵
在 中
答:轮船航行的距离AD约为20km.
7.D ∵斜坡CD的坡度(或坡比)为
(米).故选D.
8.答案 20
解析 设斜坡AB的坡角为α.∵斜面AB的坡度为1:∴°.
∵在P处测得A处的俯角为15°,B处的俯角为60°,∴∠HBP=60°,∠APB=45°.
∴∠PBA=90°.∴∠BAP=45°.∴PB=AB.米,∴米.
9.解析 (1)∵tan∠ABE=i=1:,∴∠ABE=30°.∴∠ABC=150°.
(2)如图,过M点作MN⊥CD于点N.
∵AB=20米,∠ABE=30°,米,
米. 米, 米.
米.
∵ 米.
答:电线杆CD的高度约为31米.
10.解析 (1)如图,过点D作DH⊥CE于点H.
∵斜坡CF的坡比为
设DH=x米,x>0,则CH=3x米,由勾股定理,得
即 ∴DH=2米.
答:王刚同学从点C到点D的过程中上升的高度为
(2)如图,过点D作DG⊥AB于点G,设BC=a米.
∵∠DHB=∠DGB=∠ABC=90°,∴四边形DHBG为矩形.∴DH=BG=2米,DG=BH=(a+6)米.
米.∴AG=(a-2)米.
∵∠ADG=30°,∴tan∠ADC=tan30°,即 .
米.
答:大树AB的高度是()米.
能力提升
11.C 在Rt△MCB中,∠MCB=60°,CB=30m,
∵山坡DF的坡度i=1:1.25,EF=50m,∴DE=40m.∵ ∴ND=25 m.
∴两个通信基站顶端M与顶端N的高度差故选C.
12.解析 在 中,∴
在 中,∴ ,
25.6(m),
答:旗杆AB的高度约为5.6m.
13.解析 如图,过点A作AD⊥BC,垂足为D,
在 中, (米),
则 米.
在 中, 米≈1960米.
过点P作 垂足为E,
则
∵BE+AE=AB,即 米,∴PE≈726米.
答:A庄与B庄的距离约为1960米,山高约为726米.
14.解析 (1)由题意,得∠BAC=45°+30°=75°,∠ABC=180°-60°-45°=75°,
∴∠C=180°-∠ABC-∠BAC=180°-75°-75°=30°.
(2)如图,过点B作BG⊥AD于G,则∠AGB=∠BGD=90°.
在Rt△AGB中,AB=20米,∠BAG=45°,∴AG=BG=20×sin45°=10(米).
在Rt△BGD中,∠BDG=60°,米 米.
∵∠C=∠CAD=30°,∴CD=AD=AG+DG= 米.
米.
答:两棵银杏树B、C之间的距离为 米.
15.解析 (1)如图,过点P 作P M⊥AC于M,设.
在Rt△P AM中,由题意可得∠P AM=45°,∴.
在Rt△P CM中,由题意可得∠P CM=30°,∴
解得
∴
∴A处到临皋亭 处的距离为
(2)如图,过点B作 于N.
∵
在中,∵ ∴
在Rt△P BN中,∵∠P =60°,∴
又
∴临皋亭P 处与遗爱亭P 处之间的距离是
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
5 三角函数的应用
基础过关
知识点1 三角函数的应用——仰角、俯角问题
1.如图,在C处测得旗杆AB的顶端A的仰角为30°,向旗杆前进10米到达D处,在D处测得A的仰角为60°,则旗杆的高为( )
米 B.10米 米 米
2.某高铁线路规划中,需要确定河流的宽度AB的长.已知在离地面600 m高度C处的无人机上,测得正前方A,B两点处的俯角分别为60°和45°,则河流的宽度AB的长为多
少米 (结果保留根号)
3.在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是53°,从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°,综合楼高24米.请你帮小明求出办公楼的高度.(结果精确到0.1,参考数据:
4.如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为30°,已知
求乙楼的高度AC的长.(参考数据: ≈1.73,精确到0.1m)
知识点2 三角函数的应用——方向角问题
5.为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习.如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向距离A处.学生分成两组,第一组前往A地,
第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是 第二组乘公交车,速度是,两组同学到达目的地分别用了多长时间 哪组同学先到达目的地 请说明理由(结果保留根号).
6.如图,在港口A处的正东方向有两个相距6 km的观测点B,C.一艘轮船从A处出发,沿北偏东26°方向航行至D处,在B,C处分别测得∠ABD=45°,∠C=37°.求轮船航行
的距离AD.(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49, sin 37°≈0.60,cos37°≈0.80, tan 37°≈0.75)
知识点3 三角函数的应用——坡度、坡角问题
7.如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为 坡顶D到BC的垂直距离 米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为 则建筑物AB的高度约为( )
(参考数据:
A.69.2米 B.73.1米 C.80.0米 D.85.7米
8.如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面AB的坡度为1:,则斜坡AB的长是 __________米.
9.如图,防洪大堤的横截面ABGH是梯形,背水坡AB的坡度i=1: (垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠α=20°.
(1)求∠ABC的度数;
(2)求电线杆CD的高度.(结果精确到个位,参考数据:sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,≈1.7)
10.王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走 米到达斜坡上D点,在点D处测得树顶端A的仰角为 若斜坡CF的坡比为 (点E、C、B在同一水平线上).
(1)求王刚同学从点C到点D的过程中上升的高度;
(2)求大树AB的高度(结果保留根号).
能力提升
11.如图,相邻两个山坡上,分别有垂直于水平面的通信基站MA和ND.甲在山脚点C处测得通信基站顶端M的仰角为60°,测得点C距离通信基站MA的水平距离CB为30 m;乙在另一座山脚点F处测得点F距离通信基站ND的水平距离FE为50 m,测得山坡DF的坡度i=1:1.25.若 DE,点C,B,E,F在同一水平线上,则两个通信基站顶端M与顶端N的高度差为(参考数据: ( )
A.9.0 m B.12.8 m C.13.1 m D.22.7 m
12.如图,建筑物BC上有一旗杆AB,从与BC相距20 m的D处观测旗杆顶部A的仰角为52°,观测旗杆底部B的仰角为45°,求旗杆AB的高度(结果保留到小数点后一位.参考数据:
13.如图,在小山的东侧A庄有一热气球,由于受西风的影响,以每分钟35m的速度沿着与水平方向成角的方向飞行,40 min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为 求A庄与B庄的距离及山高(参考数据: 结果精确到个位).
14.小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向,C在北偏东 方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.
(1)求 的度数;
(2)求两棵银杏树B,C之间的距离(结果保留根号).
15.[数学建模]因东坡文化远近闻名的遗爱湖公园,“国庆黄金周”期间,游人络绎不绝,现有一艘游船载着游客在遗爱湖中游览,如图,当船在A处时,船上游客发现岸上 处的临皋亭和处的遗爱亭都在东北方向;当游船向正东方向行驶600m到达B处时,游客发现遗爱亭在北偏西 方向;当游船继续向正东方向行驶400 m到达C处时,游客发现临皋亭在北偏西 方向.
(1)求A处到临皋亭 处的距离;
(2)求临皋亭P 处与遗爱亭 处之间的距离.(计算结果保留根号)
参考答案
基础过关
1.C 由题意得∠C=30°,∠ADB=60°,∴∠DAC=∠ADB-∠C=30°.∴∠DAC=∠C.
∴AD=DC=10米.在Rt△ADB中, (米).故选C.
2.解析 由题意得∠COA=90°,∠CAO=60°,∠CBO=600 m.∴
3.解析 在Rt△ABD中,AB=24米,∠BDA=53°,∠BAD=90°,∴
在Rt△ACD中,∠CDA=90°,∠CAD=30°,∴(米).故办公楼的高度约为10.4米.
4.解析 过点E作EFLAC于F,则四边形CDEF为矩形.
∴EF=CD,CF=DE=10m.易知∠EBF=60°,∠DAC=45°,
设AC=x m,则CD=EF=x m,BF=(x-16)m,
在Rt△BEF中,∠EBF=60°,, ∴
答:乙楼的高度AC的长约为37.8m.
5.解析 如图,过点B作BD⊥AC于D.
由题意得,∠BAE=45°,∠ABC=180°-45°-30°=105°.
又∠CAE=15°,∴∠BAC=30°,∴∠ACB=45°.设BD=x km.
在Rt△BCD中,∠DCB=45°=∠CBD,∴CD=BD=x km,BC=
在Rt△BDA中,
解得
第一组用时:
第二组用时:
∴第二组先到达目的地.
6.解析 如图,过点D作 于点H.
在 中, 在Rt△DBH中, ∵
在 中
答:轮船航行的距离AD约为20km.
7.D ∵斜坡CD的坡度(或坡比)为
(米).故选D.
8.答案 20
解析 设斜坡AB的坡角为α.∵斜面AB的坡度为1:∴°.
∵在P处测得A处的俯角为15°,B处的俯角为60°,∴∠HBP=60°,∠APB=45°.
∴∠PBA=90°.∴∠BAP=45°.∴PB=AB.米,∴米.
9.解析 (1)∵tan∠ABE=i=1:,∴∠ABE=30°.∴∠ABC=150°.
(2)如图,过M点作MN⊥CD于点N.
∵AB=20米,∠ABE=30°,米,
米. 米, 米.
米.
∵ 米.
答:电线杆CD的高度约为31米.
10.解析 (1)如图,过点D作DH⊥CE于点H.
∵斜坡CF的坡比为
设DH=x米,x>0,则CH=3x米,由勾股定理,得
即 ∴DH=2米.
答:王刚同学从点C到点D的过程中上升的高度为
(2)如图,过点D作DG⊥AB于点G,设BC=a米.
∵∠DHB=∠DGB=∠ABC=90°,∴四边形DHBG为矩形.∴DH=BG=2米,DG=BH=(a+6)米.
米.∴AG=(a-2)米.
∵∠ADG=30°,∴tan∠ADC=tan30°,即 .
米.
答:大树AB的高度是()米.
能力提升
11.C 在Rt△MCB中,∠MCB=60°,CB=30m,
∵山坡DF的坡度i=1:1.25,EF=50m,∴DE=40m.∵ ∴ND=25 m.
∴两个通信基站顶端M与顶端N的高度差故选C.
12.解析 在 中,∴
在 中,∴ ,
25.6(m),
答:旗杆AB的高度约为5.6m.
13.解析 如图,过点A作AD⊥BC,垂足为D,
在 中, (米),
则 米.
在 中, 米≈1960米.
过点P作 垂足为E,
则
∵BE+AE=AB,即 米,∴PE≈726米.
答:A庄与B庄的距离约为1960米,山高约为726米.
14.解析 (1)由题意,得∠BAC=45°+30°=75°,∠ABC=180°-60°-45°=75°,
∴∠C=180°-∠ABC-∠BAC=180°-75°-75°=30°.
(2)如图,过点B作BG⊥AD于G,则∠AGB=∠BGD=90°.
在Rt△AGB中,AB=20米,∠BAG=45°,∴AG=BG=20×sin45°=10(米).
在Rt△BGD中,∠BDG=60°,米 米.
∵∠C=∠CAD=30°,∴CD=AD=AG+DG= 米.
米.
答:两棵银杏树B、C之间的距离为 米.
15.解析 (1)如图,过点P 作P M⊥AC于M,设.
在Rt△P AM中,由题意可得∠P AM=45°,∴.
在Rt△P CM中,由题意可得∠P CM=30°,∴
解得
∴
∴A处到临皋亭 处的距离为
(2)如图,过点B作 于N.
∵
在中,∵ ∴
在Rt△P BN中,∵∠P =60°,∴
又
∴临皋亭P 处与遗爱亭P 处之间的距离是
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
