6.2垂直关系的性质[下学期]
图片预览




文档简介
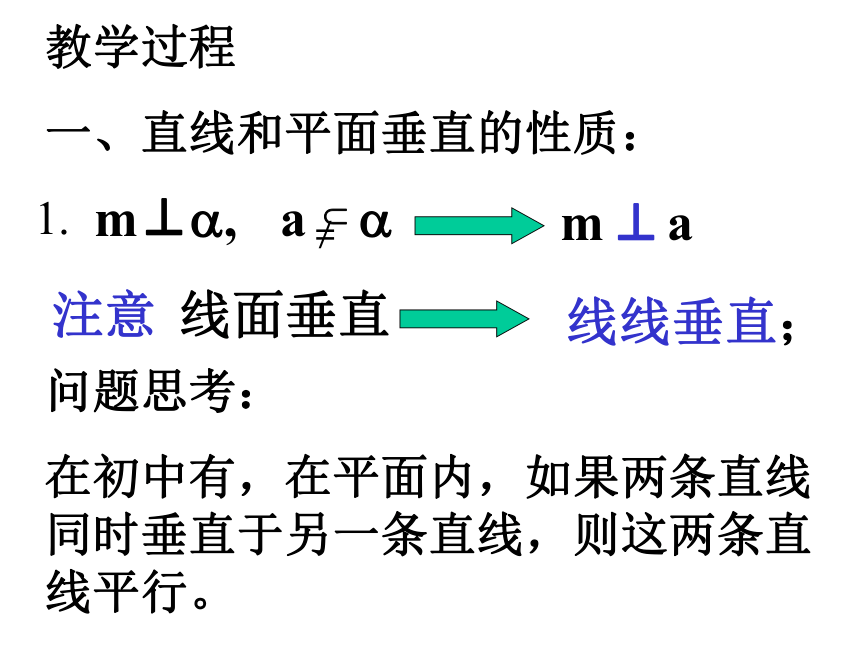
课件20张PPT。6.2垂直关系的性质教学目标及重点
1.通过本节教学,掌握线面垂直及面面垂直的性质,提高学生空间想象能力.
2.通过问题解决,提高等价转化思想渗透的意识.
3.进一步提高学生分析问题、解决问题的能力.教学难点:直线与平面垂直及两个平面垂直的性质定理运用.
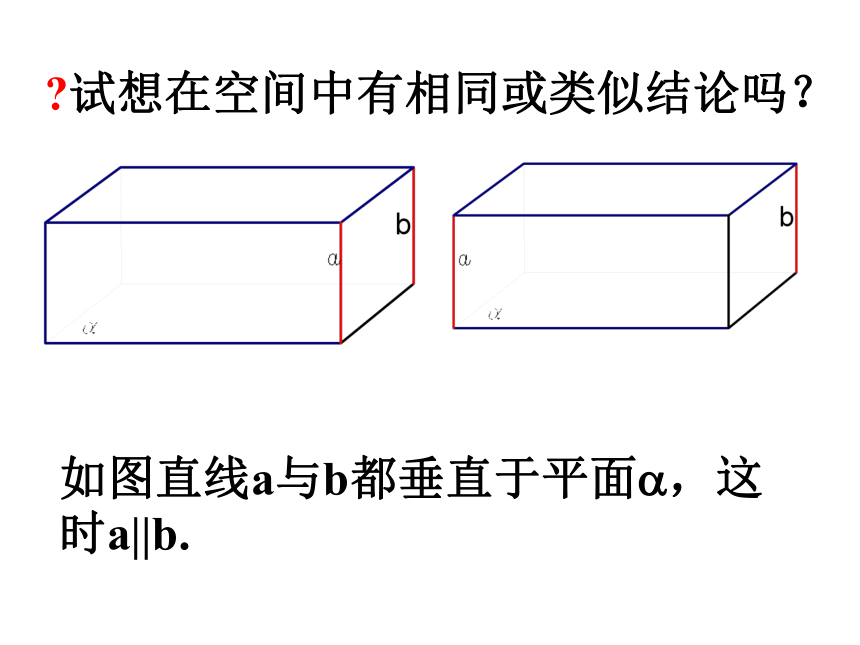
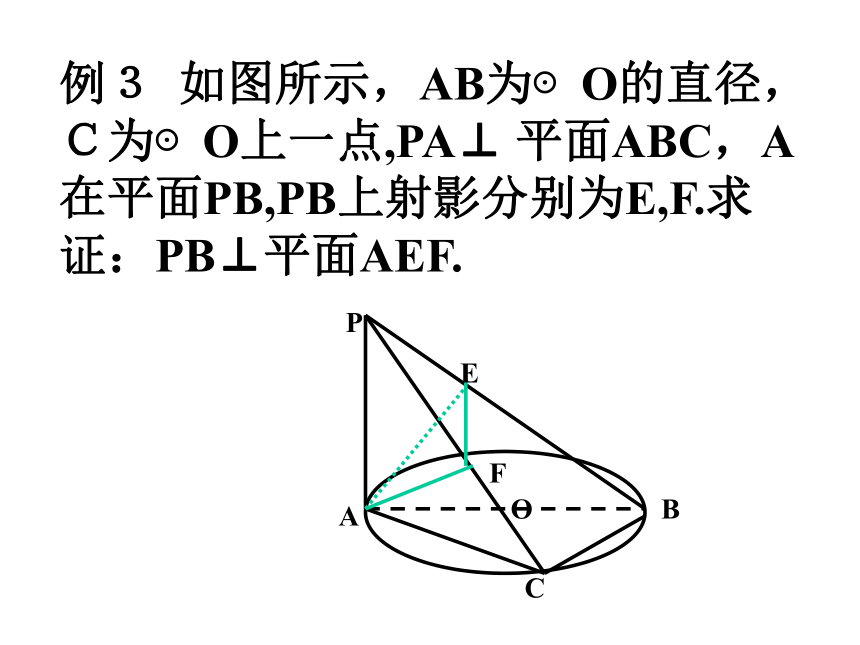
突破方法:通过典型习题的讲解、剖析,及设置相关问题引导学生思考来突破难点。如图直线a与b都垂直于平面?,这时a||b.?试想在空间中有相同或类似结论吗?例3 如图所示,AB为⊙O的直径,C为⊙O上一点,PA⊥ 平面ABC,A在平面PB,PB上射影分别为E,F.求证:PB⊥平面AEF.思考:
1.从例3图中你可以得出几组互相垂直的平面?分别是什么?
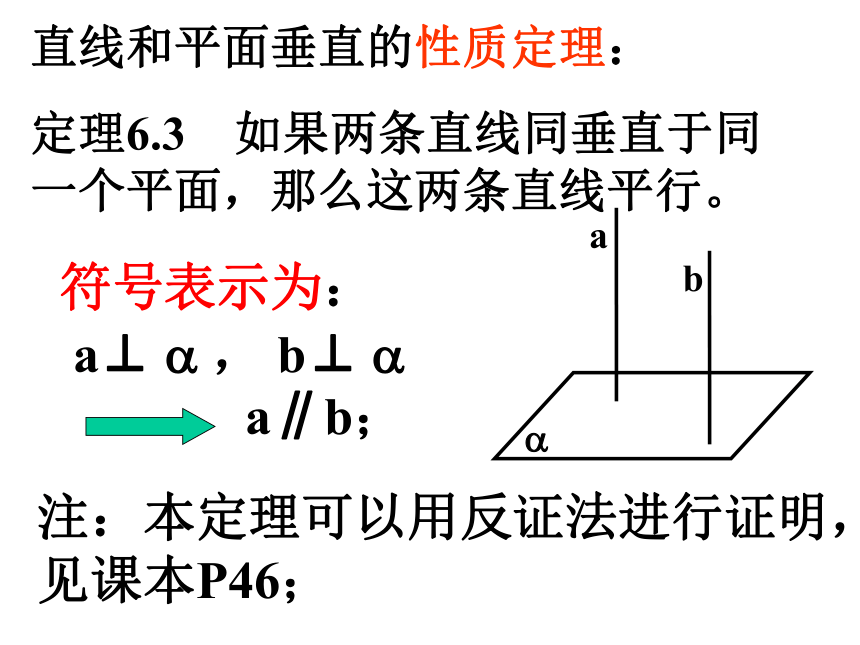
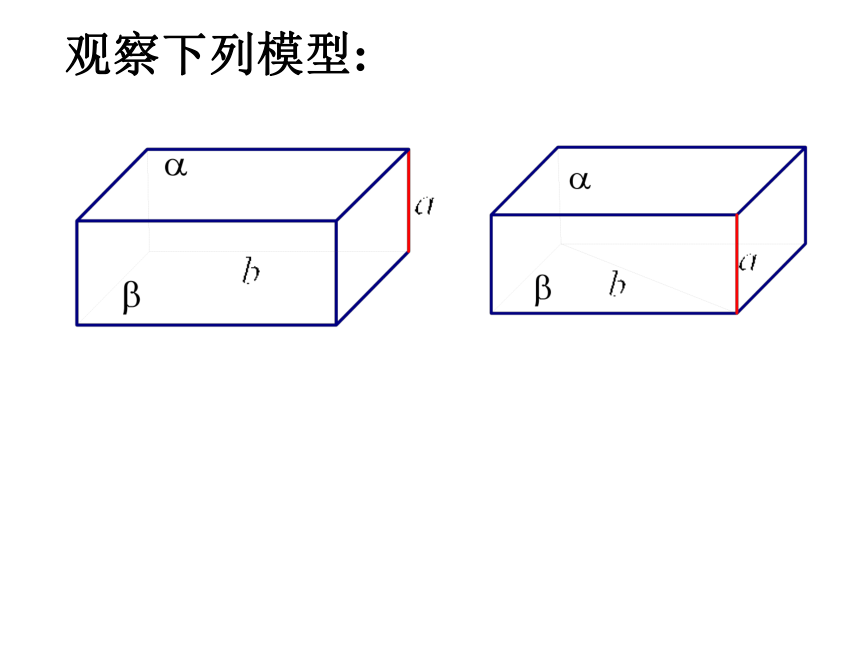
2.如果保持例3图中点F不动,让点E在直线PB上运动,那么平面AEF与平面PBC的位置关系有不没有变化?观察下列模型:两个平面垂直的性质定理:
定理6.4 如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一平面.数学符号例4如图,长方体ABCD-A’B’C’D’中,MN在平面BCC’B’内,MN?BC于M,判断MN与AB的位置关系,并说明理由。 MN和哪些直线垂直。又有哪些平面和MN平行?P48、练习:1、2、3
P49、B 1。基础计算推理
1、已知如图,平面?⊥平面? ,在?与 ?内的交线上取线段AB=4,AC,BD分别在平面?和平面? 内,它们垂直于交线AB,并且AC=3cm,BD=12cm,求CD的长。答案CD=13cm2、已知Rt△ABC中,AB=AC=a,
AD是斜边BC上的高,以AD为折痕使∠BDC成直角。
求证(1)平面ABD⊥ 平面BDC,
(2)平面ACD⊥ 平面BDC,
(3) ∠BAC=600.3、如图,在立体图形V—ABC中,∠VAB=∠VAC=∠ABC=90°,平面VAB和平面VBC有何种位置关系?请说明理由.
4、如图α⊥β,α∩β=l,AB α,AB⊥l, BC β,DE β,BC⊥DE.
求证:AC⊥DE.提高练习:
1、如图α⊥β,α∩β=l,A∈α,B∈β,AB=a,AB与α、β所成的角分别是θ1和θ2,求点A、B在l上的射影A′、B′间的距离.解:∵A′、B′分别是A、B在棱l上的射影,则AA′⊥l,BB′⊥l,而α⊥β
故AA′⊥β,BB′⊥α
则∠ABA′=θ2,
∠BAB′=θ1
因AB′=acosθ1,
AA′=asinθ2
故A′B′=
小结:
1、能运用直线与平面垂直、平面与平面垂直及其性质定理解决较为复习的问题;
2、理解推理中的作、证、算、答的基本步骤。
作业:P49 B,3。
P68 A,11
1.通过本节教学,掌握线面垂直及面面垂直的性质,提高学生空间想象能力.
2.通过问题解决,提高等价转化思想渗透的意识.
3.进一步提高学生分析问题、解决问题的能力.教学难点:直线与平面垂直及两个平面垂直的性质定理运用.
突破方法:通过典型习题的讲解、剖析,及设置相关问题引导学生思考来突破难点。如图直线a与b都垂直于平面?,这时a||b.?试想在空间中有相同或类似结论吗?例3 如图所示,AB为⊙O的直径,C为⊙O上一点,PA⊥ 平面ABC,A在平面PB,PB上射影分别为E,F.求证:PB⊥平面AEF.思考:
1.从例3图中你可以得出几组互相垂直的平面?分别是什么?
2.如果保持例3图中点F不动,让点E在直线PB上运动,那么平面AEF与平面PBC的位置关系有不没有变化?观察下列模型:两个平面垂直的性质定理:
定理6.4 如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一平面.数学符号例4如图,长方体ABCD-A’B’C’D’中,MN在平面BCC’B’内,MN?BC于M,判断MN与AB的位置关系,并说明理由。 MN和哪些直线垂直。又有哪些平面和MN平行?P48、练习:1、2、3
P49、B 1。基础计算推理
1、已知如图,平面?⊥平面? ,在?与 ?内的交线上取线段AB=4,AC,BD分别在平面?和平面? 内,它们垂直于交线AB,并且AC=3cm,BD=12cm,求CD的长。答案CD=13cm2、已知Rt△ABC中,AB=AC=a,
AD是斜边BC上的高,以AD为折痕使∠BDC成直角。
求证(1)平面ABD⊥ 平面BDC,
(2)平面ACD⊥ 平面BDC,
(3) ∠BAC=600.3、如图,在立体图形V—ABC中,∠VAB=∠VAC=∠ABC=90°,平面VAB和平面VBC有何种位置关系?请说明理由.
4、如图α⊥β,α∩β=l,AB α,AB⊥l, BC β,DE β,BC⊥DE.
求证:AC⊥DE.提高练习:
1、如图α⊥β,α∩β=l,A∈α,B∈β,AB=a,AB与α、β所成的角分别是θ1和θ2,求点A、B在l上的射影A′、B′间的距离.解:∵A′、B′分别是A、B在棱l上的射影,则AA′⊥l,BB′⊥l,而α⊥β
故AA′⊥β,BB′⊥α
则∠ABA′=θ2,
∠BAB′=θ1
因AB′=acosθ1,
AA′=asinθ2
故A′B′=
小结:
1、能运用直线与平面垂直、平面与平面垂直及其性质定理解决较为复习的问题;
2、理解推理中的作、证、算、答的基本步骤。
作业:P49 B,3。
P68 A,11
