11.3.2多边形的内角和课件(33张幻灯片)
文档属性
| 名称 | 11.3.2多边形的内角和课件(33张幻灯片) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-21 18:31:02 | ||
图片预览







文档简介
(共33张PPT)
生活是数学的源泉,我们是数学学习的主人.
掌握多边形内角和公式,并学会运用公式进行计算。
教学目标
1、掌握多边形内角和公式
2、正确运用多边形内角和公式
教学重点
如何把多边形转化成三角形,用分割多边形推导多边形的内角和。
教学难点
1、回答下面问题:
(1)三角形的内角和等于 。
(2)三角形的一个外角等于_______________________________
__________________的和。
(3)长方形的内角和等于 ,正方形的
内角和等于 。
180°
360°
360°
与它不相邻的
两个内角
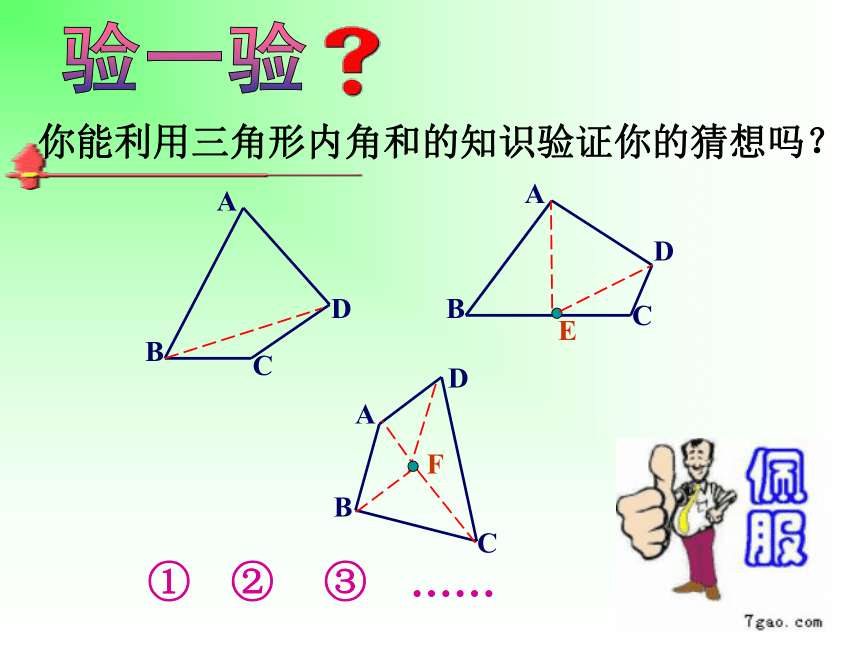
问题1:任意四边形的内角和是多少度呢?
问题2:你能利用三角形内角和的知识验证你的猜想吗?你有几种方法?
360°
A
B
C
D
A
B
C
D
A
B
C
D
F
E
①
③
②
……
你能利用三角形内角和的知识验证你的猜想吗?
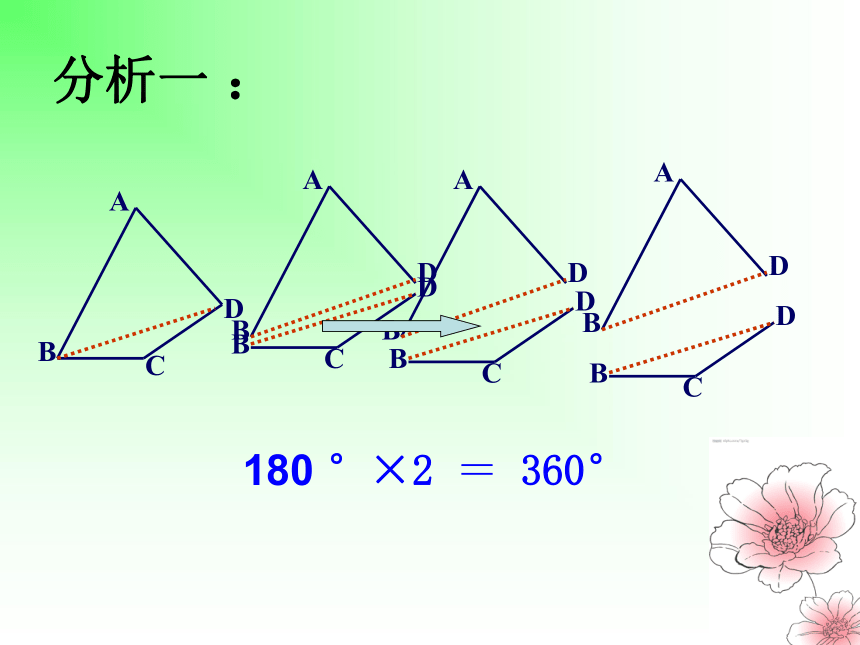
180 °×2 = 360°
A
B
C
D
A
B
D
C
B
D
A
B
D
C
B
D
A
B
D
C
B
D
分析一 :
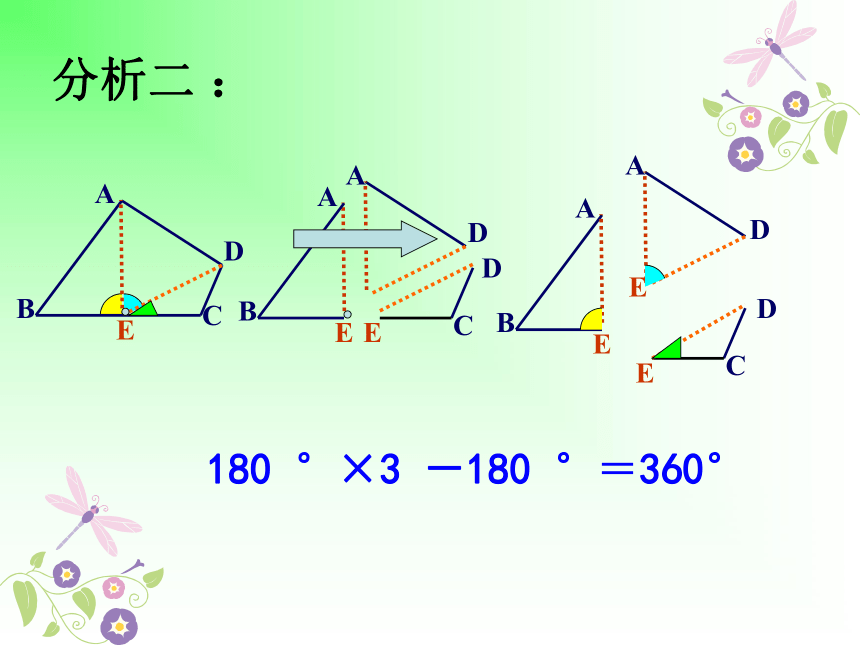
分析二 :
180 °×3 -180 °=360°
A
B
C
D
A
D
E
E
A
B
C
D
E
A
B
E
A
D
E
C
E
D
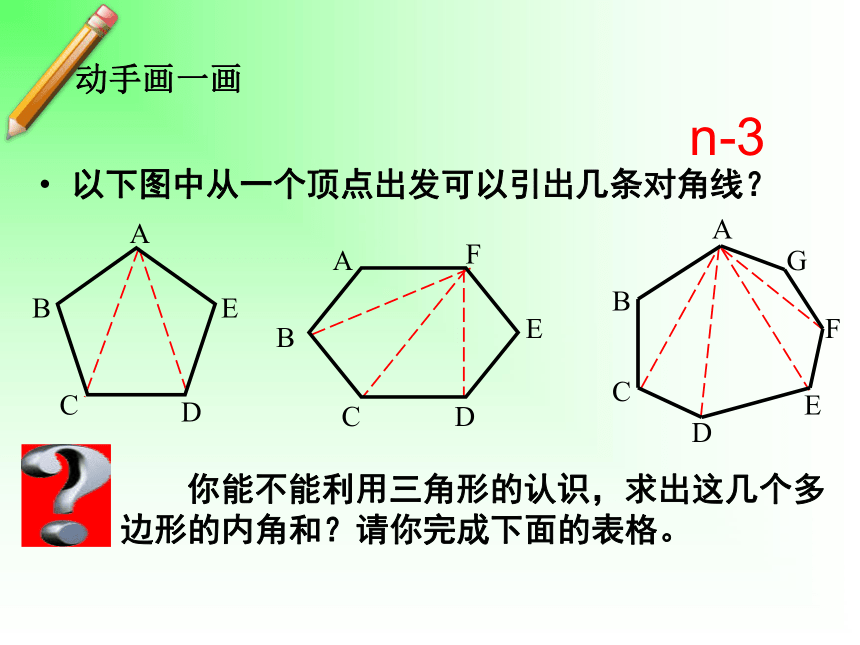
动手画一画
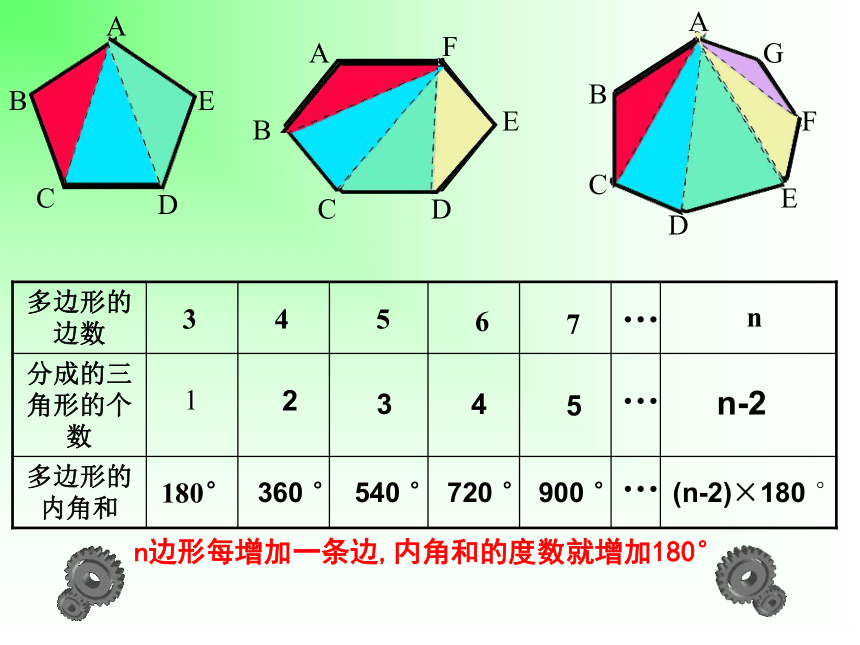
你能不能利用三角形的认识,求出这几个多边形的内角和?请你完成下面的表格。
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
E
F
G
以下图中从一个顶点出发可以引出几条对角线?
n-3
多边形的内角和
分成的三角形的个数
多边形的边数
1
…
180°
…
3
4
5
6
7
…
n
A
B
C
D
E
A
B
C
D
E
F
G
A
B
C
D
E
F
2
3
4
5
n-2
(n-2)×180 °
900 °
720 °
540 °
360 °
n边形每增加一条边,内角和的度数就增加180°
思考:n边形分成几个三角形如何表示? n边形的内角和又如何表示?
A
B
C
D
B
A
C
E
D
B
F
E
D
C
A
四边形
180 °×2= 360 °
180 ° ×3= 540 °
五边形
180 ° ×4= 720 °
六边形
(4-2)
(5-2)
(6-2)
(n-2)
(n-2) × 180 °
n边形的内角和等于
(n-2)·180°
根据以上的探讨,就得出了多边形的内角和公式:
这里的字母n是指大于或等于3的正整数
我学习!我快乐!
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
想一想:这两种分割方法你又能不能求出多边形的内角和?
(1)八边形的内角和是 ____。
(2)十边形的内角和是____。
(3)一个多边形的内角和是1800°,它是 ________边形。
(8-2)×180o=1080o
(10-2)×180o=1440o
(n-2)×180o=1800o
n=12
1、12边形的内角和等于_______
2、如果一个多边形的内角和等于1440°,那么这是___边形
1800°
十
已知边数求多边形内角和
已知多边形内角和求边数
(12-2)×180°=1800°
(n-2)×180°=1440°
n=10
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
A
C
B
D
解:因为∠A+∠B+∠C+∠D=360°
所以∠ B+∠D =360°-(∠A+∠C)
=360°-180°
=180°
如果四边形一组对角互补,那么另一组对角也互补。
例题讲解
变式:如图,OB⊥AB,垂足为B,OC⊥AC,垂足为C,试判断∠A与∠1有什么关系?
C
A
B
O
1
例题变式
已知一个多边形,它的内角和等于720°,求这个多边形的边数。
解: 设多边形的边数为n,
(n-2) 180°= 720 。
解得: n=6
这个多边形的边数为6。
例题讲解
已知一个多边形,它的内角和等于五边形的内角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n,
(n-2) 180°=2×540 。
解得: n=8
这个多边形的边数8。
学以致用
1、求下列图形中x的值:
(2)
∟
(1)
巩固提高
2、一个正多边形的每一个内角都等于135°,则这个多边形是几边形?
解:设这个多边形是n边形,由题意得
(n-2)×180o=n × 135o
解得:n=8
答:这个多边形是八边形。
巩固提高
1、若一个多边形的内角和等于1080°,则这个多边形的边数是_______。
2、七边形的内角和等于_______。
3、正五边形的每个内角是________。
4、下列角度中,不能成为多边形的内角和的是( )
(A)540° (B)580° (C)1800° (D)900°
5、从n边形的一个顶点出发画对角线,最多可以画_____条,这些对角线把n边形分成_____个三角形。
当堂检测
8
900°
108°
B
n-3
n-2
如图,求∠A+∠B+∠C+∠D+∠E+∠F的值。
F
A
B
C
D
E
N
M
K
T
H
巩固提高
(1)小明每从一条小路转到下一条小路时,身体转过的角是哪个角?
(2)猜想他每跑完一圈,身体转过的角度之和是多少?
♀
清晨 ,小明沿一个五边形广场周围的小路按逆时针方向跑步。
议一议
1.十边形的内角和是________;
2.(a+1)边形的内角和是________.
小组竞赛A组
1440°
(a-1)180°
1.一个多边形的内角和等于1440°,是__ 边形。
2.一个多边形的内角和为720°,那么这个多边
形的对角线条数为( )
A.6条 B.7条 C.8条 D.9条
3.一个多边形的内角和是1800°, 那么这个
多边形是( )
A.五边形 B.八边形
C.十边形 D.十二边形
小组竞赛B组
十
D
D
1.一个多边形的每个内角都等于135°,则这个多边形为 边形.
2.内角和等于外角和的多边形是 边形.
3.多边形每个内角都相等,内角和为720°,
则它的每一个外角为 .
小组竞赛C组
八
四
60°
4.随着多边形的边数n的增加,它的外角和( )
A.增加 B.减小 C.不变 D.不定
5.一个多边形每个外角都是60°,这个多边形的
外角和为( )
A.180° B.360° C.720° D.1080°
小组竞赛C组
D
C
(2009年嘉兴市)在四边形ABCD中,∠D=60°,∠B 比∠A大20°,∠C是∠A的2倍,求∠A,∠B,∠C的大小.
小组竞赛D组
∠A =70o
∠B =90o
∠C =140o
①多边形的内角和公式。
(n-2)·180°
②用转化以及方程思想解决问题。
③由特殊到一般研究问题的方法。
回味无穷
数轴人生
追求无最值需解好人生方程
岁月有极限当选准人生坐标
结束寄语
下课啦
生活是数学的源泉,我们是数学学习的主人.
掌握多边形内角和公式,并学会运用公式进行计算。
教学目标
1、掌握多边形内角和公式
2、正确运用多边形内角和公式
教学重点
如何把多边形转化成三角形,用分割多边形推导多边形的内角和。
教学难点
1、回答下面问题:
(1)三角形的内角和等于 。
(2)三角形的一个外角等于_______________________________
__________________的和。
(3)长方形的内角和等于 ,正方形的
内角和等于 。
180°
360°
360°
与它不相邻的
两个内角
问题1:任意四边形的内角和是多少度呢?
问题2:你能利用三角形内角和的知识验证你的猜想吗?你有几种方法?
360°
A
B
C
D
A
B
C
D
A
B
C
D
F
E
①
③
②
……
你能利用三角形内角和的知识验证你的猜想吗?
180 °×2 = 360°
A
B
C
D
A
B
D
C
B
D
A
B
D
C
B
D
A
B
D
C
B
D
分析一 :
分析二 :
180 °×3 -180 °=360°
A
B
C
D
A
D
E
E
A
B
C
D
E
A
B
E
A
D
E
C
E
D
动手画一画
你能不能利用三角形的认识,求出这几个多边形的内角和?请你完成下面的表格。
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
E
F
G
以下图中从一个顶点出发可以引出几条对角线?
n-3
多边形的内角和
分成的三角形的个数
多边形的边数
1
…
180°
…
3
4
5
6
7
…
n
A
B
C
D
E
A
B
C
D
E
F
G
A
B
C
D
E
F
2
3
4
5
n-2
(n-2)×180 °
900 °
720 °
540 °
360 °
n边形每增加一条边,内角和的度数就增加180°
思考:n边形分成几个三角形如何表示? n边形的内角和又如何表示?
A
B
C
D
B
A
C
E
D
B
F
E
D
C
A
四边形
180 °×2= 360 °
180 ° ×3= 540 °
五边形
180 ° ×4= 720 °
六边形
(4-2)
(5-2)
(6-2)
(n-2)
(n-2) × 180 °
n边形的内角和等于
(n-2)·180°
根据以上的探讨,就得出了多边形的内角和公式:
这里的字母n是指大于或等于3的正整数
我学习!我快乐!
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
想一想:这两种分割方法你又能不能求出多边形的内角和?
(1)八边形的内角和是 ____。
(2)十边形的内角和是____。
(3)一个多边形的内角和是1800°,它是 ________边形。
(8-2)×180o=1080o
(10-2)×180o=1440o
(n-2)×180o=1800o
n=12
1、12边形的内角和等于_______
2、如果一个多边形的内角和等于1440°,那么这是___边形
1800°
十
已知边数求多边形内角和
已知多边形内角和求边数
(12-2)×180°=1800°
(n-2)×180°=1440°
n=10
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
A
C
B
D
解:因为∠A+∠B+∠C+∠D=360°
所以∠ B+∠D =360°-(∠A+∠C)
=360°-180°
=180°
如果四边形一组对角互补,那么另一组对角也互补。
例题讲解
变式:如图,OB⊥AB,垂足为B,OC⊥AC,垂足为C,试判断∠A与∠1有什么关系?
C
A
B
O
1
例题变式
已知一个多边形,它的内角和等于720°,求这个多边形的边数。
解: 设多边形的边数为n,
(n-2) 180°= 720 。
解得: n=6
这个多边形的边数为6。
例题讲解
已知一个多边形,它的内角和等于五边形的内角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n,
(n-2) 180°=2×540 。
解得: n=8
这个多边形的边数8。
学以致用
1、求下列图形中x的值:
(2)
∟
(1)
巩固提高
2、一个正多边形的每一个内角都等于135°,则这个多边形是几边形?
解:设这个多边形是n边形,由题意得
(n-2)×180o=n × 135o
解得:n=8
答:这个多边形是八边形。
巩固提高
1、若一个多边形的内角和等于1080°,则这个多边形的边数是_______。
2、七边形的内角和等于_______。
3、正五边形的每个内角是________。
4、下列角度中,不能成为多边形的内角和的是( )
(A)540° (B)580° (C)1800° (D)900°
5、从n边形的一个顶点出发画对角线,最多可以画_____条,这些对角线把n边形分成_____个三角形。
当堂检测
8
900°
108°
B
n-3
n-2
如图,求∠A+∠B+∠C+∠D+∠E+∠F的值。
F
A
B
C
D
E
N
M
K
T
H
巩固提高
(1)小明每从一条小路转到下一条小路时,身体转过的角是哪个角?
(2)猜想他每跑完一圈,身体转过的角度之和是多少?
♀
清晨 ,小明沿一个五边形广场周围的小路按逆时针方向跑步。
议一议
1.十边形的内角和是________;
2.(a+1)边形的内角和是________.
小组竞赛A组
1440°
(a-1)180°
1.一个多边形的内角和等于1440°,是__ 边形。
2.一个多边形的内角和为720°,那么这个多边
形的对角线条数为( )
A.6条 B.7条 C.8条 D.9条
3.一个多边形的内角和是1800°, 那么这个
多边形是( )
A.五边形 B.八边形
C.十边形 D.十二边形
小组竞赛B组
十
D
D
1.一个多边形的每个内角都等于135°,则这个多边形为 边形.
2.内角和等于外角和的多边形是 边形.
3.多边形每个内角都相等,内角和为720°,
则它的每一个外角为 .
小组竞赛C组
八
四
60°
4.随着多边形的边数n的增加,它的外角和( )
A.增加 B.减小 C.不变 D.不定
5.一个多边形每个外角都是60°,这个多边形的
外角和为( )
A.180° B.360° C.720° D.1080°
小组竞赛C组
D
C
(2009年嘉兴市)在四边形ABCD中,∠D=60°,∠B 比∠A大20°,∠C是∠A的2倍,求∠A,∠B,∠C的大小.
小组竞赛D组
∠A =70o
∠B =90o
∠C =140o
①多边形的内角和公式。
(n-2)·180°
②用转化以及方程思想解决问题。
③由特殊到一般研究问题的方法。
回味无穷
数轴人生
追求无最值需解好人生方程
岁月有极限当选准人生坐标
结束寄语
下课啦
