11.4镶嵌 (20张幻灯片)
文档属性
| 名称 | 11.4镶嵌 (20张幻灯片) |

|
|
| 格式 | zip | ||
| 文件大小 | 993.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-21 18:37:30 | ||
图片预览







文档简介
课件20张PPT。11.4课题学习镶嵌问题情境请同学们欣赏下面的图画:当你欣赏这些美丽图案时,你是否想到这些图案中所蕴含的数学道理呢? 在这些图案拼成的地面或墙面上,相邻的地砖或瓷砖平整地贴合在一起,整个地面或墙面没有一点空隙.
不重叠摆放的多边形把平面的一部分完全覆盖,这类问题称为多边形覆盖平面(或平面镶嵌).想一想:
1、用同一种正多边形进行镶嵌,需要满足什么条件?
2、只有哪几种正多边形可以进行这样的镶嵌?
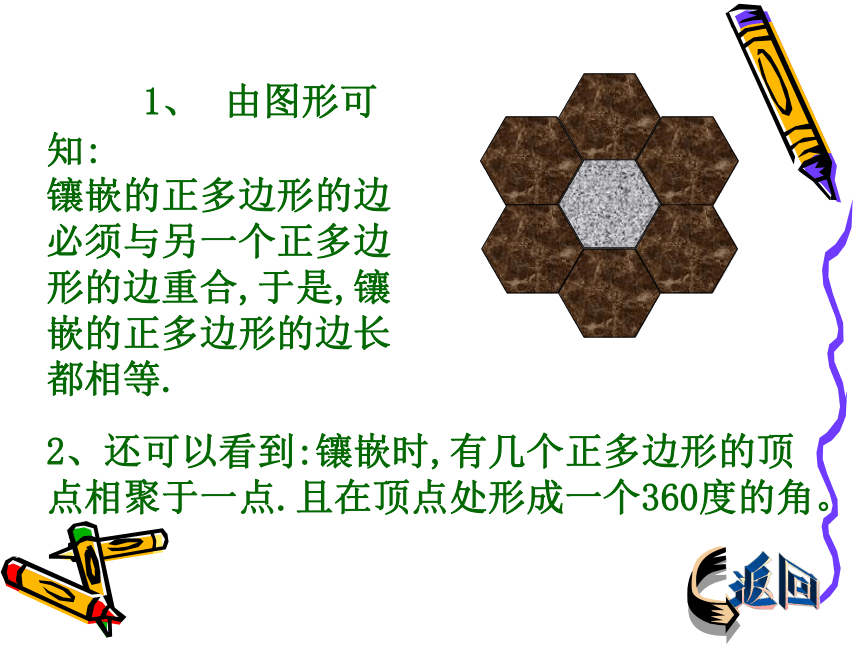
探究活动1演示1演示2几何画板演示跳出 1、 由图形可知:
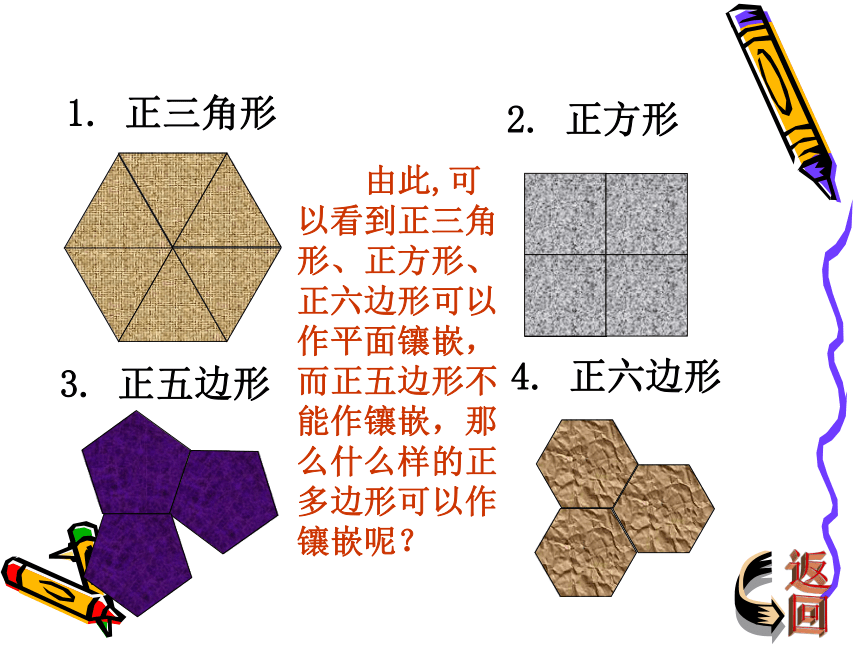
镶嵌的正多边形的边必须与另一个正多边形的边重合,于是,镶嵌的正多边形的边长都相等.2、还可以看到:镶嵌时,有几个正多边形的顶点相聚于一点.且在顶点处形成一个360度的角。返回1. 正三角形2. 正方形3. 正五边形4. 正六边形 由此,可以看到正三角形、正方形、正六边形可以作平面镶嵌,而正五边形不能作镶嵌,那么什么样的正多边形可以作镶嵌呢?返回=360 °k·此式可化为:(n-2)(k-2)=4因为n、k为正整数,所以n-2和k-2是4的正因数,于是有:或或解得:或或几何画板演示由以上分析和讨论可知: 由一种正多边形进行镶嵌,只能有三种情况:( 1 )正三角形( 2 )正方形( 3 )正六边形end 问题:由两种或两种以上的正多边形进行镶嵌,有几种情况呢?探究活动2几何画板演示到思考2 m+3 n=12m=3
n=2设在一个顶点周围有 m 个正三角形的角,n 个正方形的角,
则有
∵ m,n 为正整数∴解为三角形和正方形m+2 n=6m=2
n=2m=4
n=1设在一个顶点周围有 m 个正三角形的角,n 个正六边形的角,则有:∵ m,n 为正整数∴解为正三角形和正六边形2 m+5 n=12m=1
n=2设在一个顶点周围有 m 个正三角形的角,n 个正十二边形
的角,则有∵ m,n 为正整数∴解为正三角形和正十二边形2 m+3 n=8m=1
n=2正四边形正八边形设在一个顶点周围有个 m 正四边形的角,n 个正八边形
的角,则有∵ m,n 为正整数∴解为设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有3 m+4 n=10m=2
n=1∵ m,n 为正整数∴解 为五边形和正十边形 1、同一种任意三角形可否镶嵌成一个平面?
2、 同一种任意四边形可否镶嵌成一个平面?思考:小红的妈妈准备把一些形状,大小相同的三角形花布丢掉
小红:妈妈,这些花布很好看,您为什么要丢掉呢?
妈妈:小红,这些布是很漂亮,可是面积太小,做不了什么东西
只好丢掉!
小红:别扔,让我想想办法,把这些布头拼成一块漂亮的桌布吧。结论:形状、大小完全相同的任意三角形能镶嵌成平面图形。在一个工厂的废料堆里,正堆放着大量的四边形木块,这些废木块
的大小、形状是一样的,它们既不是正方形,也不是长方形,都是
不规则的四边形,如果把它们做成比较规则的形状,必须剧掉一些
边角,就要浪费很多木料,有人建议用这些木料来铺地板!同学们
说说行吗?结论:形状、大小相同的任意四边形能镶嵌成平面图形1 、平面镶嵌的定义.
2 、镶嵌的意义、条件、作用、方法.
3 、关注身边的数学,关注数学中的美.
总结:1、若限用一种正多边形镶嵌,不可能是( )
A、正三角形 B、正方形 C、正五边形 D、正六边形
2、用两种正多边形镶嵌不能与正三角形匹配的正多边形是( )
A、正方形 B、正六边形 C、正十二边形 D、正十七边形
3、明明家若想用边长相同的两种正多边形水泥砖铺地面,若其中一种为正六边形的水泥砖,请你帮助选择,你会再选择哪一种正多边形的水泥砖,试着画出 示意图。4、(2000。安徽)我们常见到的如图那样的地面,它们分别是全用正方形或全用
正六边形形状的材料铺成的这样形状的材料能铺成平整、无空隙的地面 补偿提高祝同学们学习进步!谢谢大家!
不重叠摆放的多边形把平面的一部分完全覆盖,这类问题称为多边形覆盖平面(或平面镶嵌).想一想:
1、用同一种正多边形进行镶嵌,需要满足什么条件?
2、只有哪几种正多边形可以进行这样的镶嵌?
探究活动1演示1演示2几何画板演示跳出 1、 由图形可知:
镶嵌的正多边形的边必须与另一个正多边形的边重合,于是,镶嵌的正多边形的边长都相等.2、还可以看到:镶嵌时,有几个正多边形的顶点相聚于一点.且在顶点处形成一个360度的角。返回1. 正三角形2. 正方形3. 正五边形4. 正六边形 由此,可以看到正三角形、正方形、正六边形可以作平面镶嵌,而正五边形不能作镶嵌,那么什么样的正多边形可以作镶嵌呢?返回=360 °k·此式可化为:(n-2)(k-2)=4因为n、k为正整数,所以n-2和k-2是4的正因数,于是有:或或解得:或或几何画板演示由以上分析和讨论可知: 由一种正多边形进行镶嵌,只能有三种情况:( 1 )正三角形( 2 )正方形( 3 )正六边形end 问题:由两种或两种以上的正多边形进行镶嵌,有几种情况呢?探究活动2几何画板演示到思考2 m+3 n=12m=3
n=2设在一个顶点周围有 m 个正三角形的角,n 个正方形的角,
则有
∵ m,n 为正整数∴解为三角形和正方形m+2 n=6m=2
n=2m=4
n=1设在一个顶点周围有 m 个正三角形的角,n 个正六边形的角,则有:∵ m,n 为正整数∴解为正三角形和正六边形2 m+5 n=12m=1
n=2设在一个顶点周围有 m 个正三角形的角,n 个正十二边形
的角,则有∵ m,n 为正整数∴解为正三角形和正十二边形2 m+3 n=8m=1
n=2正四边形正八边形设在一个顶点周围有个 m 正四边形的角,n 个正八边形
的角,则有∵ m,n 为正整数∴解为设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有3 m+4 n=10m=2
n=1∵ m,n 为正整数∴解 为五边形和正十边形 1、同一种任意三角形可否镶嵌成一个平面?
2、 同一种任意四边形可否镶嵌成一个平面?思考:小红的妈妈准备把一些形状,大小相同的三角形花布丢掉
小红:妈妈,这些花布很好看,您为什么要丢掉呢?
妈妈:小红,这些布是很漂亮,可是面积太小,做不了什么东西
只好丢掉!
小红:别扔,让我想想办法,把这些布头拼成一块漂亮的桌布吧。结论:形状、大小完全相同的任意三角形能镶嵌成平面图形。在一个工厂的废料堆里,正堆放着大量的四边形木块,这些废木块
的大小、形状是一样的,它们既不是正方形,也不是长方形,都是
不规则的四边形,如果把它们做成比较规则的形状,必须剧掉一些
边角,就要浪费很多木料,有人建议用这些木料来铺地板!同学们
说说行吗?结论:形状、大小相同的任意四边形能镶嵌成平面图形1 、平面镶嵌的定义.
2 、镶嵌的意义、条件、作用、方法.
3 、关注身边的数学,关注数学中的美.
总结:1、若限用一种正多边形镶嵌,不可能是( )
A、正三角形 B、正方形 C、正五边形 D、正六边形
2、用两种正多边形镶嵌不能与正三角形匹配的正多边形是( )
A、正方形 B、正六边形 C、正十二边形 D、正十七边形
3、明明家若想用边长相同的两种正多边形水泥砖铺地面,若其中一种为正六边形的水泥砖,请你帮助选择,你会再选择哪一种正多边形的水泥砖,试着画出 示意图。4、(2000。安徽)我们常见到的如图那样的地面,它们分别是全用正方形或全用
正六边形形状的材料铺成的这样形状的材料能铺成平整、无空隙的地面 补偿提高祝同学们学习进步!谢谢大家!
