第11章三角形复习之内角和外角篇(21张幻灯片)
文档属性
| 名称 | 第11章三角形复习之内角和外角篇(21张幻灯片) |  | |
| 格式 | zip | ||
| 文件大小 | 228.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-21 18:44:28 | ||
图片预览


文档简介
(共21张PPT)
________之“内角外角”篇
三角形
与三角形有关的线段
三角形内角和
三角形外角和
知识结构图
与三角形有关的角
内角与外角关系
三角形的分类
多边形
多边形的内角和
多边形的外角和
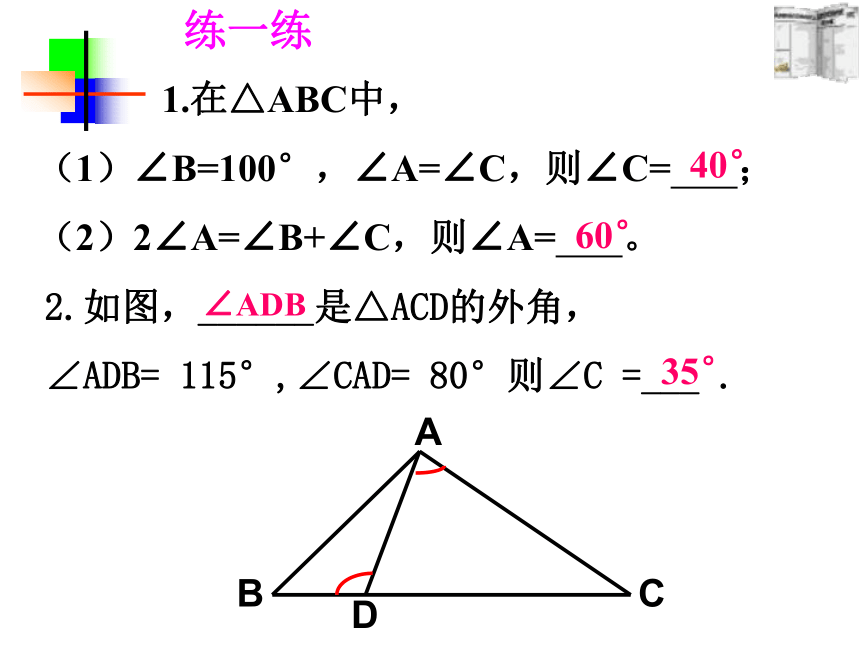
1.在△ABC中,
(1)∠B=100°,∠A=∠C,则∠C= ;
(2)2∠A=∠B+∠C,则∠A= 。
2.如图,______是△ACD的外角,
∠ADB= 115°,∠CAD= 80°则∠C =___ .
40°
60°
35°
A
B
C
D
∠ADB
练一练
5、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数,
C
解:设每个外角为x度.则每个内角为(3x+20)度
由邻补角定义得:x+(3x+20)=180
解得:x=40
所以多边形的边数为:360÷40=9.
所以这是一个9边形.
3.直角三角形的两个锐角相等,则每一个锐角等于_____度。
45
4、一个多边形每一个外角都等于45°,则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°
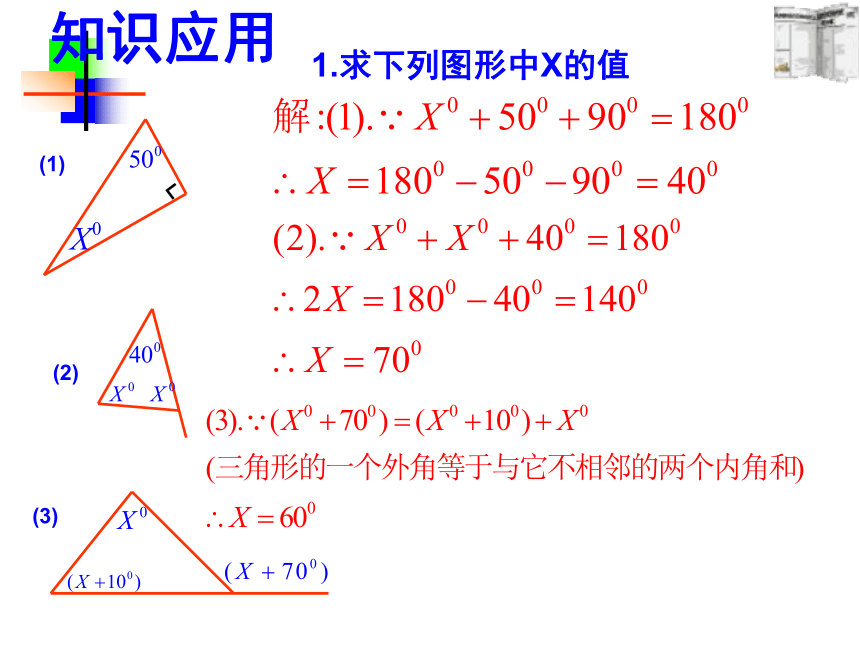
1.求下列图形中X的值
(3)
(2)
(1)
┛
知识应用
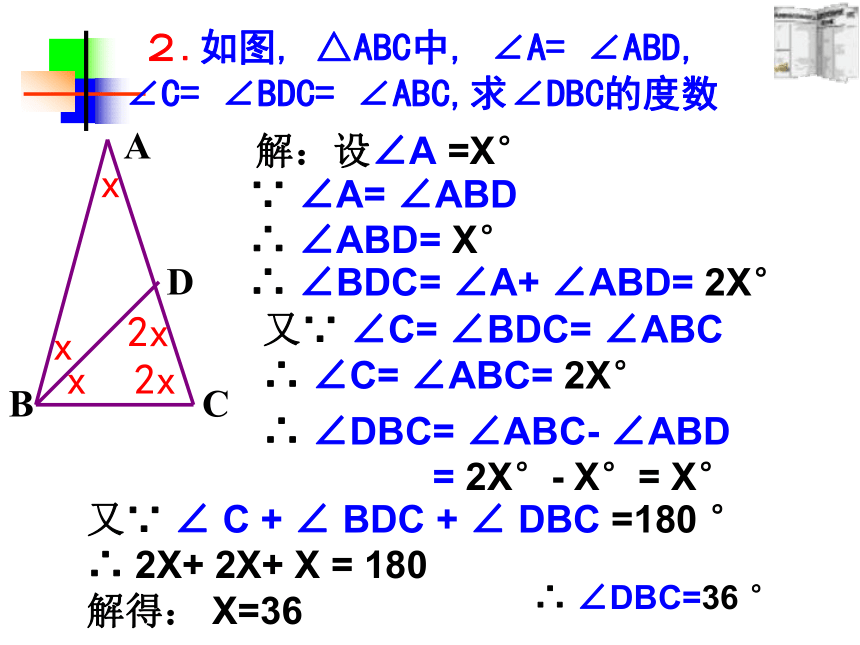
2.如图, △ABC中, ∠A= ∠ABD,
∠C= ∠BDC= ∠ABC,求∠DBC的度数
A
B
C
D
x
x
2x
2x
解:设∠A =X°
∵ ∠A= ∠ABD
∴ ∠ABD= X°
∴ ∠BDC= ∠A+ ∠ABD= 2X°
又∵ ∠C= ∠BDC= ∠ABC
∴ ∠C= ∠ABC= 2X°
∴ ∠DBC= ∠ABC- ∠ABD
= 2X°- X°= X°
又∵ ∠ C + ∠ BDC + ∠ DBC =180 °
∴ 2X+ 2X+ X = 180
解得: X=36
∴ ∠DBC=36 °
x
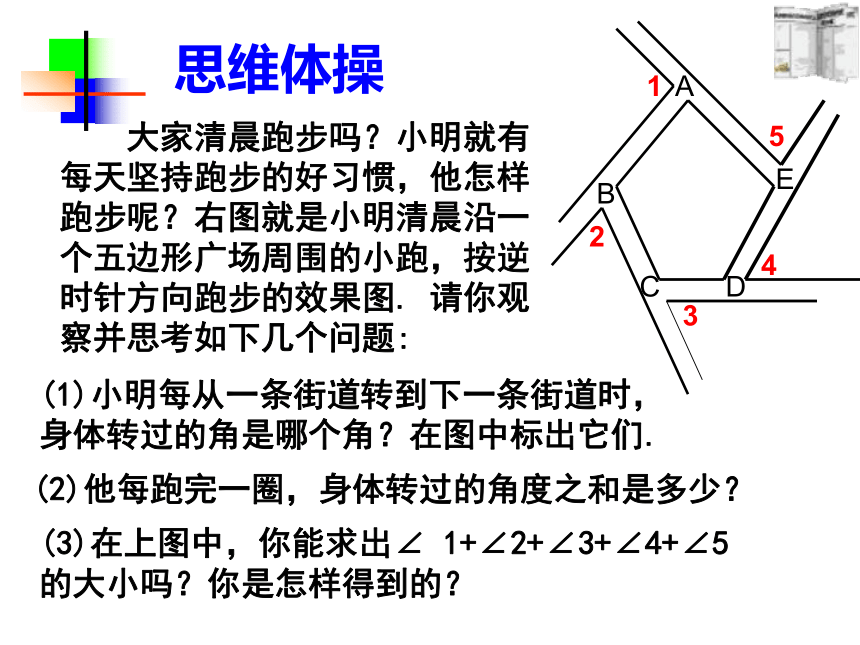
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
A
B
C
D
E
1
2
3
4
5
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出∠ 1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
思维体操
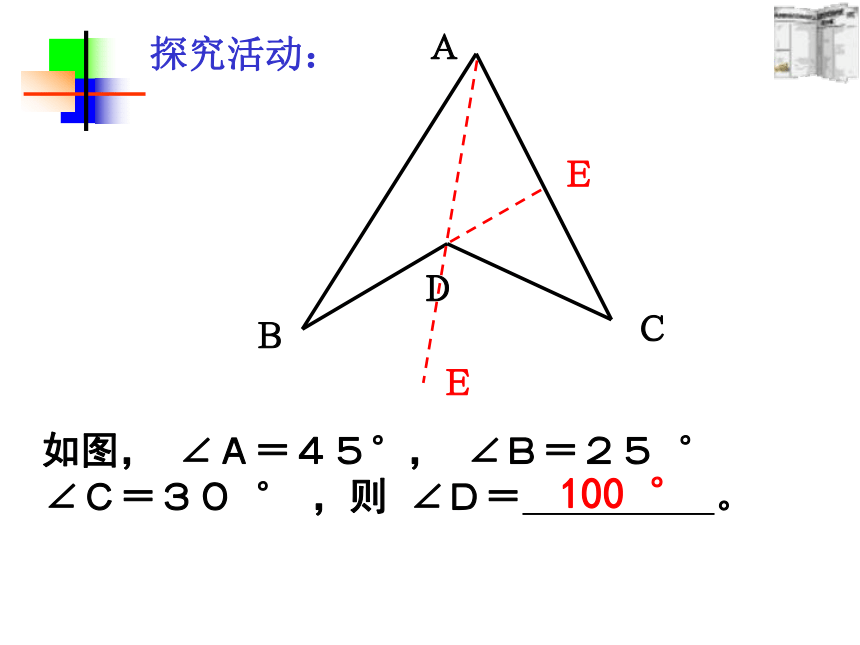
探究活动:
A
B
C
D
如图, ∠A=45°, ∠B=25 ° ∠C=30 ° ,则 ∠D= 。
E
E
100 °
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
G
180 °
G
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
1
2
3
4
5
180 °
巩固一下:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
7×180O-2×360O=540O
1. 三角形内角和定理
三角形的内角和等于1800
直角三角形的两个锐角互余。
2. 三角形外角和定理
三角形的外角和等于3600
三角形的一个外角等于与它不相邻的两个内角的和。
3. 三角形的外角与内角的关系
三角形的一个外角大于与它不相邻的任何一个内角。
小结
4、n边形的内角和等于(n-2)·180 .
多边形的外角和都等于360°.
我们通过把多边形划分为若干个三角形,用三角形内角和去求多边形内角和,从而得到多边形的内角和公式为(n-2)× 180°。这种化未知为已知的转化方法,必须在学习中逐渐掌握。由于多边形外角和为360°,与边数无关,所以常把多边形内角和的问题转化为外角和来处理。
三角形三个内角的度数分别是(x+y)o, (x-y)o,xo,且x>y>0,则该三角形有一个内角为 ( )
A、30O B、45O C、60O D、90O
2.一个正多边形每一个内角都是120o,这个多边形是( ) A、正四边形 B、正五边形
C、正六边形 D、正七边形
C
C
3.一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160o,则原多边形的边数为( )
A、13条 B、14条 C、15条 D、16条
下列说法中,错误的是( )
A、一个三角形中至少有一个角不大于60O; B、有一个外角是锐角的三角形是钝角三角形;C、三角形的外角中必有两个角是钝角; D、锐角三角形中两锐角的和必然小于60O;
A
D
5.小明绕五边形各边走一圈,他共转了_ __度。
6.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是 ;
360
(1)、(2)、(4)
7.如下图,AD是BC边上的高,BE是 △ ABD的角平分线,∠1=40°,∠2=30°,则∠C=_ __∠BED= 。
65°
60°
A
B
C
D
1
2
E
8、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
2、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
A
B
C
X
1
2
3
4
________之“内角外角”篇
三角形
与三角形有关的线段
三角形内角和
三角形外角和
知识结构图
与三角形有关的角
内角与外角关系
三角形的分类
多边形
多边形的内角和
多边形的外角和
1.在△ABC中,
(1)∠B=100°,∠A=∠C,则∠C= ;
(2)2∠A=∠B+∠C,则∠A= 。
2.如图,______是△ACD的外角,
∠ADB= 115°,∠CAD= 80°则∠C =___ .
40°
60°
35°
A
B
C
D
∠ADB
练一练
5、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数,
C
解:设每个外角为x度.则每个内角为(3x+20)度
由邻补角定义得:x+(3x+20)=180
解得:x=40
所以多边形的边数为:360÷40=9.
所以这是一个9边形.
3.直角三角形的两个锐角相等,则每一个锐角等于_____度。
45
4、一个多边形每一个外角都等于45°,则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°D、945°
1.求下列图形中X的值
(3)
(2)
(1)
┛
知识应用
2.如图, △ABC中, ∠A= ∠ABD,
∠C= ∠BDC= ∠ABC,求∠DBC的度数
A
B
C
D
x
x
2x
2x
解:设∠A =X°
∵ ∠A= ∠ABD
∴ ∠ABD= X°
∴ ∠BDC= ∠A+ ∠ABD= 2X°
又∵ ∠C= ∠BDC= ∠ABC
∴ ∠C= ∠ABC= 2X°
∴ ∠DBC= ∠ABC- ∠ABD
= 2X°- X°= X°
又∵ ∠ C + ∠ BDC + ∠ DBC =180 °
∴ 2X+ 2X+ X = 180
解得: X=36
∴ ∠DBC=36 °
x
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
A
B
C
D
E
1
2
3
4
5
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出∠ 1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
思维体操
探究活动:
A
B
C
D
如图, ∠A=45°, ∠B=25 ° ∠C=30 ° ,则 ∠D= 。
E
E
100 °
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
G
180 °
G
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
1
2
3
4
5
180 °
巩固一下:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
7×180O-2×360O=540O
1. 三角形内角和定理
三角形的内角和等于1800
直角三角形的两个锐角互余。
2. 三角形外角和定理
三角形的外角和等于3600
三角形的一个外角等于与它不相邻的两个内角的和。
3. 三角形的外角与内角的关系
三角形的一个外角大于与它不相邻的任何一个内角。
小结
4、n边形的内角和等于(n-2)·180 .
多边形的外角和都等于360°.
我们通过把多边形划分为若干个三角形,用三角形内角和去求多边形内角和,从而得到多边形的内角和公式为(n-2)× 180°。这种化未知为已知的转化方法,必须在学习中逐渐掌握。由于多边形外角和为360°,与边数无关,所以常把多边形内角和的问题转化为外角和来处理。
三角形三个内角的度数分别是(x+y)o, (x-y)o,xo,且x>y>0,则该三角形有一个内角为 ( )
A、30O B、45O C、60O D、90O
2.一个正多边形每一个内角都是120o,这个多边形是( ) A、正四边形 B、正五边形
C、正六边形 D、正七边形
C
C
3.一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160o,则原多边形的边数为( )
A、13条 B、14条 C、15条 D、16条
下列说法中,错误的是( )
A、一个三角形中至少有一个角不大于60O; B、有一个外角是锐角的三角形是钝角三角形;C、三角形的外角中必有两个角是钝角; D、锐角三角形中两锐角的和必然小于60O;
A
D
5.小明绕五边形各边走一圈,他共转了_ __度。
6.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是 ;
360
(1)、(2)、(4)
7.如下图,AD是BC边上的高,BE是 △ ABD的角平分线,∠1=40°,∠2=30°,则∠C=_ __∠BED= 。
65°
60°
A
B
C
D
1
2
E
8、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
2、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
A
B
C
X
1
2
3
4
