第11章三角形全章知识点复习和配套练习课件(33张幻灯片)
文档属性
| 名称 | 第11章三角形全章知识点复习和配套练习课件(33张幻灯片) |  | |
| 格式 | zip | ||
| 文件大小 | 93.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-21 18:48:43 | ||
图片预览








文档简介
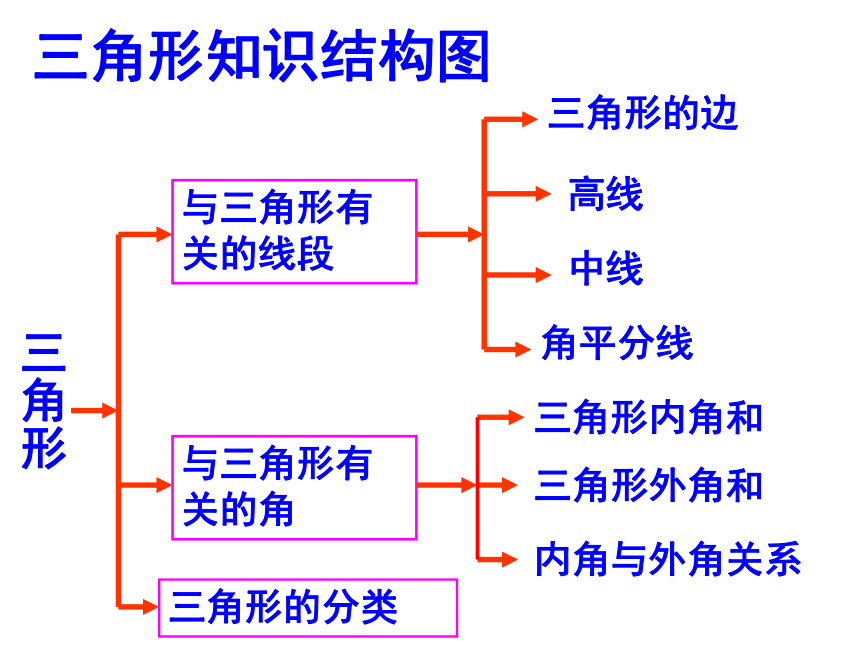
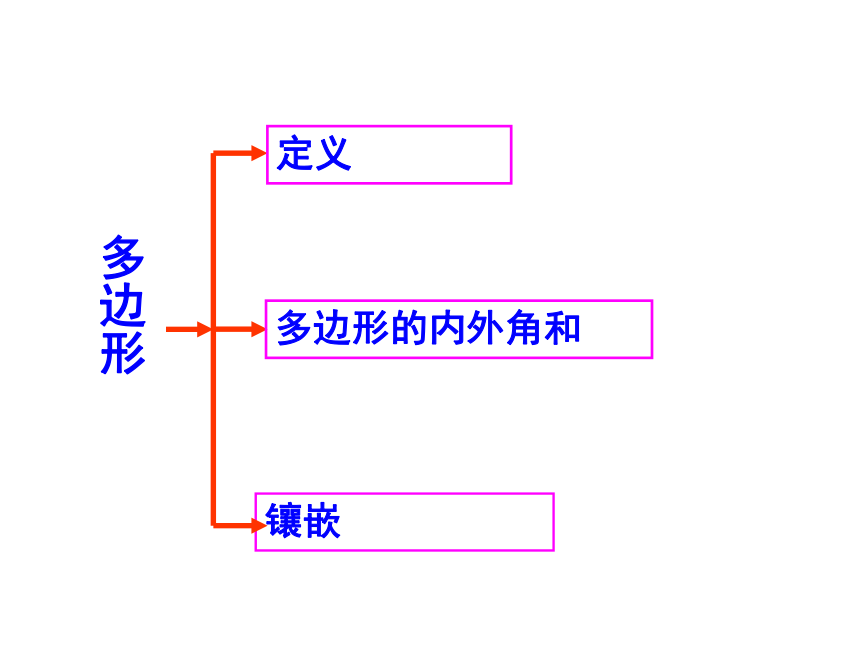
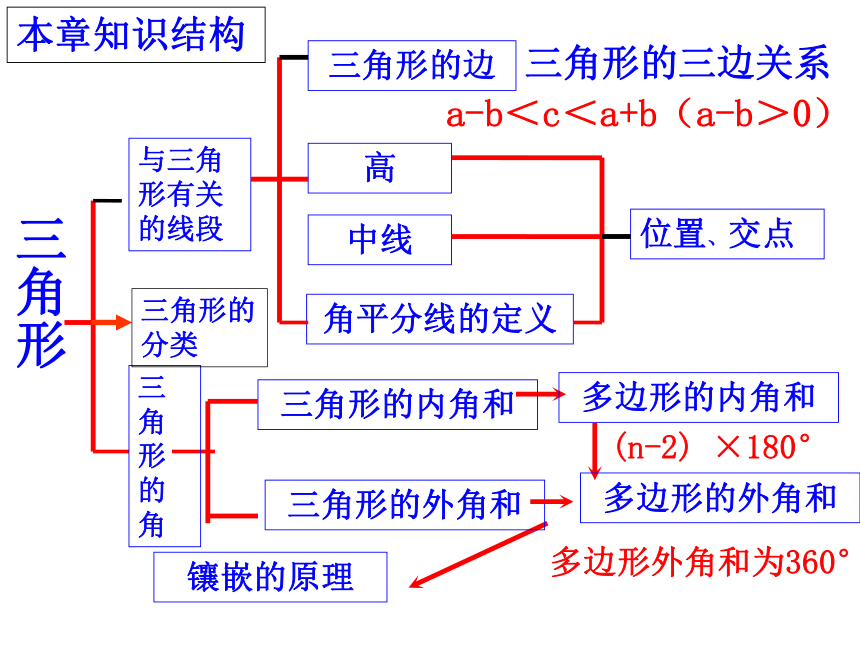
课件33张PPT。第11章三角形复习三角形与三角形有关的线段三角形内角和三角形外角和三角形知识结构图三角形的边高线中线角平分线与三角形有关的角内角与外角关系三角形的分类多边形定义多边形的内外角和镶嵌(n-2) ×180°三角形与三角形有关的线段a-b<c<a+b(a-b>0)高三角形的边三角形的三边关系中线角平分线的定义位置、交点三角形的内角和多边形的内角和多边形的外角和三角形的外角和多边形外角和为360°镶嵌的原理本章知识结构三角形的角三角形的分类1. 三角形的三边关系:(1) 三角形两边的和大于第三边2. 判断三条已知线段a、b、c能否
组成三角形.当a最长,且有b+c>a时,就可构成三角形.3. 确定三角形第三边的取值范围:两边之差<第三边<两边之和.(2) 三角形两边的差小于第三边知识要点4. 三角形的分类锐角三角形三角形钝角三角形(1) 按角分直角三角形斜三角形(2) 按边分腰和底不等的等腰三角形三角形等腰三角形等边三角形不等边三角形1、下列条件中能组成三角形的是( ) A、 5cm, 13cm, 7cm
B、 3cm, 5cm, 9cm C、 14cm, 9cm, 6cm
D、 5cm, 6cm, 11cm 2、三角形的两边为7cm和5cm,则第三边x的
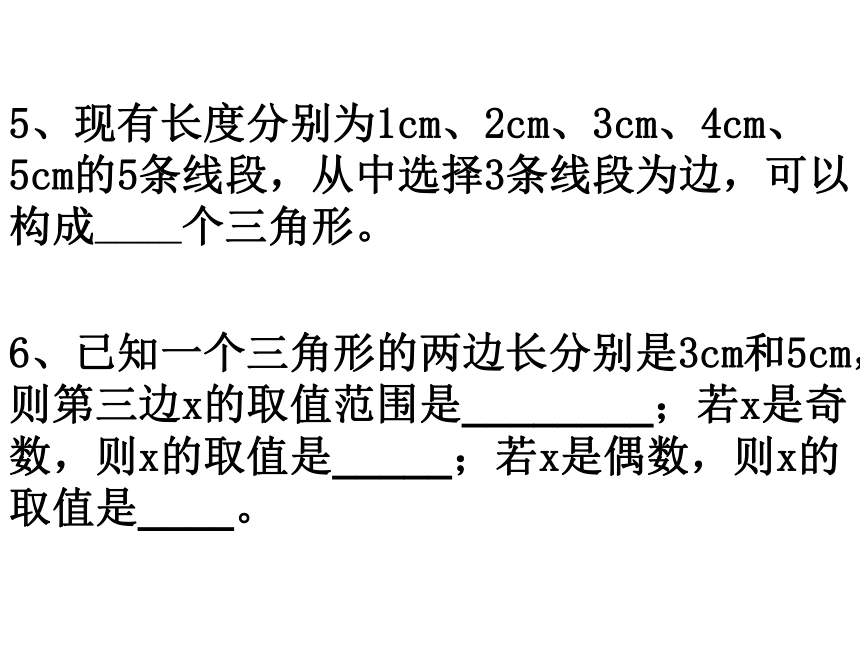
范围是_____________;练一练3、根据所给条件判断△ABC的形状(是锐角三角形、直角三角形还是钝角三角形)(1)∠A=75°,∠B=83°;(2)∠A=35°,∠B=55°;(3)∠A=20°,∠B=30°;5、现有长度分别为1cm、2cm、3cm、4cm、5cm的5条线段,从中选择3条线段为边,可以构成________个三角形。6、已知一个三角形的两边长分别是3cm和5cm,则第三边x的取值范围是________;若x是奇数,则x的取值是_____;若x是偶数,则x的取值是____。7、已知等腰三角形的两边长是4cm和8cm,则这个三角形的周长是_______cm。8、若一个等腰三角形的周长是28cm,有一边长是6cm,求这个三角形的其他两边长。从三角形的一个顶点向它的对边所在直线作垂线,_______________的线段叫做三角形的高线.三角形的高线定义:顶点和垂足之间5 三角形的主要线段三角形角平分线的定义:顶点与交点三角形的中线定义顶点与它对边中点6 三角形的三条高线(或高线所在直线)
交于一点锐角三角形三条高线交于三角形内部一点,直角三角形三条高线交于直角顶点,钝角三角形三条高线所在直线交于三角形
外部一点。7 三角形的三条中线交于三角形内部一点。8 三角形的三条角平分线交于三角形
内部一点。9、画△ABC中BC边上的高,下列各图中正确的是( )ABCABCDD练一练10、AD是△ABC的边BC上的中线,11、如图,在△ABC中,CE,BF是两条高,若∠A=65°,∠BCE=25°,则∠EBF的度数是 ,
∠FBC的度
数是 .7.1.3三角形的稳定性12、盖房子时,房顶的支架都是选择三角形形状的,这是运用了________________的原理。9. 三角形木架的形状不会改变,而四边形木架的形状会改变.这就是说,三角形具有稳定性,而四边形没有稳定性。10. 三角形内角和定理三角形的内角和等于1800直角三角形的两个锐角互余。11. 三角形外角和定理三角形的外角和等于3600 三角形的一个外角等于与它不相邻的两个内角的和。12. 三角形的外角与内角的关系 三角形的一个外角大于与它不相邻的任何一个内角。7.2与三角形有关的角7.2.1三角形的内角13、已知△ABC,求证∠A+ ∠B+ ∠C=180°。(即证明三角形内角和定理)15、(1)在△ABC中,若∠A+ ∠B= ∠C,则此三角形为_____三角形;
(2)在△ABC中,若∠A+ ∠B<∠C,则此三角形为_____三角形;
(3)在△ABC中,已知∠C=2(∠B+∠A),则∠C= _____;
(4)已知三角形两个内角的差等于第三个内角,则他是一个_______三角形。16、三角形的内角中最多有_______个直角,_______个钝角;最少有_______个直角,_______个钝角;最多有_______个锐角,最少有_______个锐角。17、如图所示,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40 °的方向,一观测员在灯塔A处观看B和C处时的视角∠BAC是多少度?7.2.2三角形的外角18、(1)如图①,_______是△ABD的外角,______是△BCE的外角;
(2)如图②,△BFD的外角有_______,以∠AEB为外角的三角形是_______。19、若三角形的一个外角等于和它相邻的内角的2倍,则这个外角等于_______度。20、根据下图所提供的信息,求出x的值:21、三角形的三个外角中最多有_______个直角,_______个钝角;最少有_______个直角,_______个钝角;最多有_______个锐角,最少有_______个锐角。22、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列。24、如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.23、已知等腰三角形的一个外角为150°,
则它的底角为_____. 25、如图(1),已知∠A=50°,∠B=40°, ∠C=30°,则∠BDC=_______; 如图(2),已知∠A=70°,则∠BOC=_______; 如图(3),已知∠A=70°,则∠BOC=_______; 如图(4),已知∠A=70°,则∠BOC=_______;7.3多边形及其内角和7.3.1多边形26、(1)八边形从一个顶点出发可以引_____条对角线;这些对角线将八边形分成几个三角形;
(2)八边形共有______条对角线;
7.3.2多边形的内角和与外角和27、一个四边形的四个内角中,锐角的个数最多有________个;
一个四边形的四个内角中,钝角的个数最多有________个.28、十边形的内角和是_______°;
十边形的外角和是_______°;
内角和是1260°的多边形是____边。29、多边形增加一条边,那内角和增加____;30、一个多边形的每个内角都等于135°,则这个多边形是_____边形;内角和是_____。31、n边形的内角和是外角和的3倍,求n.32、n边形的内角和与外角和的比为3:2,求n.33、正n边形的每个内角与每个外角的比为 3:2,求n.34、一个多边形的每个外角都相等,且比它的内角小120°,求这个多边形的边数。35、求下列图中x的值。36、若一个四边形ABCD中,∠A, ∠B, ∠C,∠D的外角度数之比为8:3:7:6,则∠A=____; ∠B =____; ∠C =____; ∠D =____.37、记一记∠A+∠B+∠C+∠D+∠E=180°∠A+∠B+∠C+∠D+∠E+∠F=360°∠A+∠B+∠C+∠D+∠E+∠F=360°∠A+∠B+∠C+∠D+∠E+∠F+∠G=360°∠A+∠B+∠C+∠D+∠E+∠F=360°等边△ABC中,
DP+PE+PF=h38、△ABC中,∠A=65°, ∠B=75°,将三角形一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为_______。ABCC′12D7.4镶嵌39、镶嵌满足的条件:能铺满地面的多边形,围绕某一点的内角和为______。40、某商店出售下列五种形状的地砖⑴正三角形、⑵正方形、⑶正五边形、⑷正六边形、⑸正八边形,如果只选用其中一种地砖镶嵌地面,可供选择的地砖共有_____种。41、用两种正多边形进行镶嵌,不能与正三角形匹配的多边形是( )。 A.正方形 B.正六边形 C.正十二边形 D.正八边形42、某人在铺设地板时,想用边长相等的三种正多边形,若一种正多边形的一个内角是120°,则这个正多边形的边数是____;另一种是正方形,它的一个内角是____;已知他家在铺地板时在一个顶点处这三种正多边形都是一个,则第三种正多边形应是正___边形。
组成三角形.当a最长,且有b+c>a时,就可构成三角形.3. 确定三角形第三边的取值范围:两边之差<第三边<两边之和.(2) 三角形两边的差小于第三边知识要点4. 三角形的分类锐角三角形三角形钝角三角形(1) 按角分直角三角形斜三角形(2) 按边分腰和底不等的等腰三角形三角形等腰三角形等边三角形不等边三角形1、下列条件中能组成三角形的是( ) A、 5cm, 13cm, 7cm
B、 3cm, 5cm, 9cm C、 14cm, 9cm, 6cm
D、 5cm, 6cm, 11cm 2、三角形的两边为7cm和5cm,则第三边x的
范围是_____________;练一练3、根据所给条件判断△ABC的形状(是锐角三角形、直角三角形还是钝角三角形)(1)∠A=75°,∠B=83°;(2)∠A=35°,∠B=55°;(3)∠A=20°,∠B=30°;5、现有长度分别为1cm、2cm、3cm、4cm、5cm的5条线段,从中选择3条线段为边,可以构成________个三角形。6、已知一个三角形的两边长分别是3cm和5cm,则第三边x的取值范围是________;若x是奇数,则x的取值是_____;若x是偶数,则x的取值是____。7、已知等腰三角形的两边长是4cm和8cm,则这个三角形的周长是_______cm。8、若一个等腰三角形的周长是28cm,有一边长是6cm,求这个三角形的其他两边长。从三角形的一个顶点向它的对边所在直线作垂线,_______________的线段叫做三角形的高线.三角形的高线定义:顶点和垂足之间5 三角形的主要线段三角形角平分线的定义:顶点与交点三角形的中线定义顶点与它对边中点6 三角形的三条高线(或高线所在直线)
交于一点锐角三角形三条高线交于三角形内部一点,直角三角形三条高线交于直角顶点,钝角三角形三条高线所在直线交于三角形
外部一点。7 三角形的三条中线交于三角形内部一点。8 三角形的三条角平分线交于三角形
内部一点。9、画△ABC中BC边上的高,下列各图中正确的是( )ABCABCDD练一练10、AD是△ABC的边BC上的中线,11、如图,在△ABC中,CE,BF是两条高,若∠A=65°,∠BCE=25°,则∠EBF的度数是 ,
∠FBC的度
数是 .7.1.3三角形的稳定性12、盖房子时,房顶的支架都是选择三角形形状的,这是运用了________________的原理。9. 三角形木架的形状不会改变,而四边形木架的形状会改变.这就是说,三角形具有稳定性,而四边形没有稳定性。10. 三角形内角和定理三角形的内角和等于1800直角三角形的两个锐角互余。11. 三角形外角和定理三角形的外角和等于3600 三角形的一个外角等于与它不相邻的两个内角的和。12. 三角形的外角与内角的关系 三角形的一个外角大于与它不相邻的任何一个内角。7.2与三角形有关的角7.2.1三角形的内角13、已知△ABC,求证∠A+ ∠B+ ∠C=180°。(即证明三角形内角和定理)15、(1)在△ABC中,若∠A+ ∠B= ∠C,则此三角形为_____三角形;
(2)在△ABC中,若∠A+ ∠B<∠C,则此三角形为_____三角形;
(3)在△ABC中,已知∠C=2(∠B+∠A),则∠C= _____;
(4)已知三角形两个内角的差等于第三个内角,则他是一个_______三角形。16、三角形的内角中最多有_______个直角,_______个钝角;最少有_______个直角,_______个钝角;最多有_______个锐角,最少有_______个锐角。17、如图所示,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40 °的方向,一观测员在灯塔A处观看B和C处时的视角∠BAC是多少度?7.2.2三角形的外角18、(1)如图①,_______是△ABD的外角,______是△BCE的外角;
(2)如图②,△BFD的外角有_______,以∠AEB为外角的三角形是_______。19、若三角形的一个外角等于和它相邻的内角的2倍,则这个外角等于_______度。20、根据下图所提供的信息,求出x的值:21、三角形的三个外角中最多有_______个直角,_______个钝角;最少有_______个直角,_______个钝角;最多有_______个锐角,最少有_______个锐角。22、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列。24、如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.23、已知等腰三角形的一个外角为150°,
则它的底角为_____. 25、如图(1),已知∠A=50°,∠B=40°, ∠C=30°,则∠BDC=_______; 如图(2),已知∠A=70°,则∠BOC=_______; 如图(3),已知∠A=70°,则∠BOC=_______; 如图(4),已知∠A=70°,则∠BOC=_______;7.3多边形及其内角和7.3.1多边形26、(1)八边形从一个顶点出发可以引_____条对角线;这些对角线将八边形分成几个三角形;
(2)八边形共有______条对角线;
7.3.2多边形的内角和与外角和27、一个四边形的四个内角中,锐角的个数最多有________个;
一个四边形的四个内角中,钝角的个数最多有________个.28、十边形的内角和是_______°;
十边形的外角和是_______°;
内角和是1260°的多边形是____边。29、多边形增加一条边,那内角和增加____;30、一个多边形的每个内角都等于135°,则这个多边形是_____边形;内角和是_____。31、n边形的内角和是外角和的3倍,求n.32、n边形的内角和与外角和的比为3:2,求n.33、正n边形的每个内角与每个外角的比为 3:2,求n.34、一个多边形的每个外角都相等,且比它的内角小120°,求这个多边形的边数。35、求下列图中x的值。36、若一个四边形ABCD中,∠A, ∠B, ∠C,∠D的外角度数之比为8:3:7:6,则∠A=____; ∠B =____; ∠C =____; ∠D =____.37、记一记∠A+∠B+∠C+∠D+∠E=180°∠A+∠B+∠C+∠D+∠E+∠F=360°∠A+∠B+∠C+∠D+∠E+∠F=360°∠A+∠B+∠C+∠D+∠E+∠F+∠G=360°∠A+∠B+∠C+∠D+∠E+∠F=360°等边△ABC中,
DP+PE+PF=h38、△ABC中,∠A=65°, ∠B=75°,将三角形一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为_______。ABCC′12D7.4镶嵌39、镶嵌满足的条件:能铺满地面的多边形,围绕某一点的内角和为______。40、某商店出售下列五种形状的地砖⑴正三角形、⑵正方形、⑶正五边形、⑷正六边形、⑸正八边形,如果只选用其中一种地砖镶嵌地面,可供选择的地砖共有_____种。41、用两种正多边形进行镶嵌,不能与正三角形匹配的多边形是( )。 A.正方形 B.正六边形 C.正十二边形 D.正八边形42、某人在铺设地板时,想用边长相等的三种正多边形,若一种正多边形的一个内角是120°,则这个正多边形的边数是____;另一种是正方形,它的一个内角是____;已知他家在铺地板时在一个顶点处这三种正多边形都是一个,则第三种正多边形应是正___边形。
