第11章《三角形》复习学案
文档属性
| 名称 | 第11章《三角形》复习学案 |  | |
| 格式 | zip | ||
| 文件大小 | 57.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-21 18:50:40 | ||
图片预览

文档简介
第11章 《三角形》复习学案 姓名
1、三角形的定义:
不在 上的三条线段 连接而成的平面图形。
其表示方法是符号“△”后接着三个顶点字母。三角形是边数最少的多边形。
2、三角形的有关重要线段:
⑴三角形的三边:三角形的两边之和 第三边;两边之差 第三边;
△ABC的三边a、b、c中已知a、b,求c的取值范围是: <c< ;
⑵三角形的高线、中线、角平分线:①三线都经过顶点;②都是 ;③除直角三角形的两条高线在三角形的两条 边上,钝角三角形的两条高线在三角形 ,其他各线均在形内;④三条中线、三条角平分线、三条高线均交于一点:锐角三角形的高交于三角形 一点,直角三角形的高交于三角形的 点,钝角三角形的高的延长线交于三角形 一点。⑤三角形的一条中线把三角形分成两个 相等的小三角形;三条中线交点把每条中线分成 ∶ 两部分;有中线就有线段的倍分关系;⑥三角形的角平分线交点到三角形三边距离 ;有角平分线就有角的倍分关系;⑦有高就有 度的角,三角形的各边与这边上的高的乘积相等,据此可以建立方程解题:如图4中有:AB·CF=BC· = · ;⑧要能用几何语言表达三角形的三线。
3、三角形的稳定性的应用举例: ,四边形的不稳定性的应用举例: 。
4、三角形有关的角:⑴内角和等于 ;要能用推理得出结论;
⑵外角:是三角形的一边与另一边的 的夹角,外角和等于 ;
⑶三角形的一个外角等于 ,大于 ;三角形的外角与与之相邻的内角互为 ;
⑷三角形的两条内角平分线的夹角等于 与第三个角的 的和,如图5,P是△ABC的两条角平分线的交点,且∠A=α,则∠P= ;三角形的一条内角平分线和一条外角平分线的夹角等于第三个角的 ,如图6,P是△ABC的内角平分线和外角平分线的交点,且∠A=α,则∠P= ;三角形的两条外角平分线的夹角等于 与第三个角的 的差,如图7,P是△ABC的两条外角平分线的交点,且∠A=α,则∠P= ;
5、多边形:
⑴定义: 的几条线段 连接而成的平面图形;
叫正多边形;
⑵对角线:多边形中不相邻的两个顶点之间的连线。n边形从一个顶点出发有 对角线,这些对角线把n边形分成了 三角形,n边形共有 条对角线;
⑶n边形的内角和等于 ,正n边形的内角和还可以用 × 求得;
所以可以据此建立方程求边数;要能用三种割分多边形的方法求得多边形的内角和公式;
⑷多边形的外角和都等于 ,正n边形的每个内角度数可以通过180°-360°÷n求得;
⑸多边形的内角中最多有 个锐角,即外角中最多有 个钝角;要知道理由。
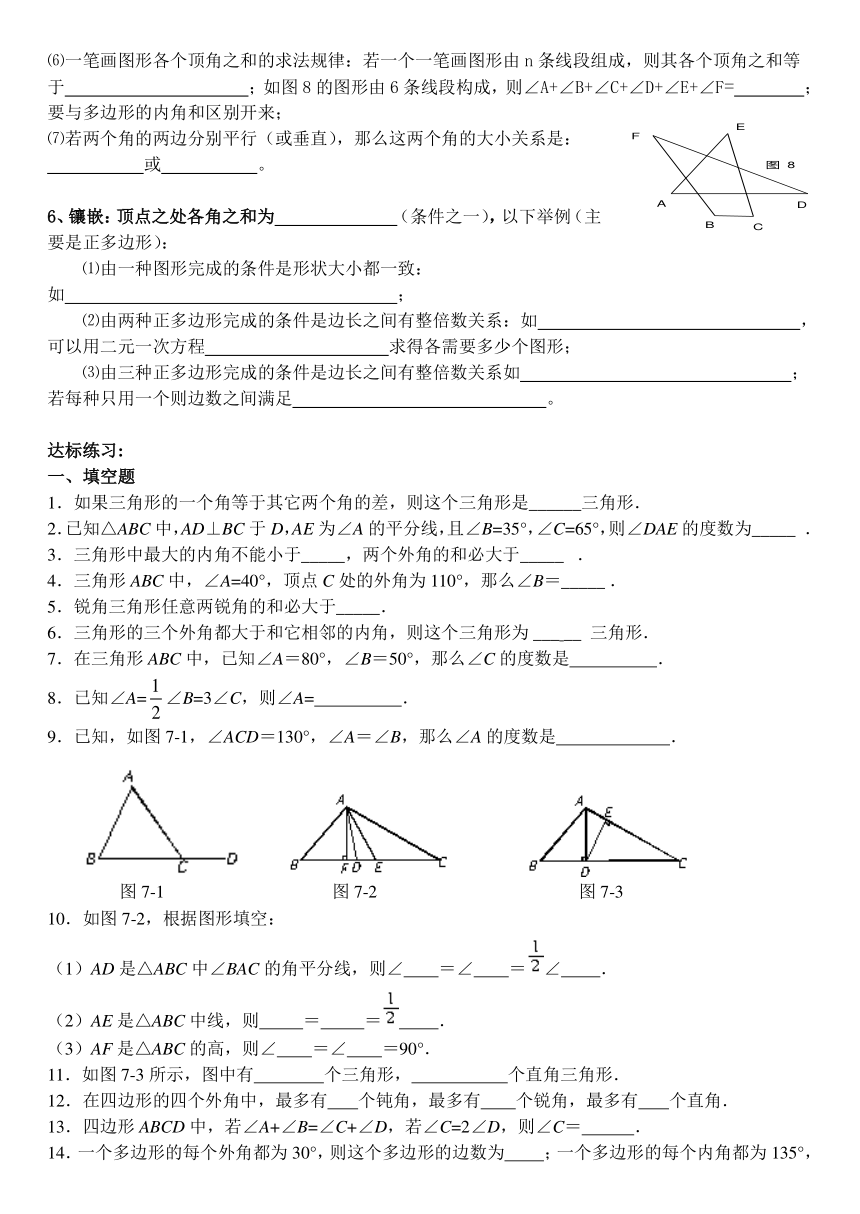
⑹一笔画图形各个顶角之和的求法规律:若一个一笔画图形由n条线段组成,则其各个顶角之和等于 ;如图8的图形由6条线段构成,则∠A+∠B+∠C+∠D+∠E+∠F= ;要与多边形的内角和区别开来;
⑺若两个角的两边分别平行(或垂直),那么这两个角的大小关系是:
或 。
6、镶嵌:顶点之处各角之和为 (条件之一),以下举例(主要是正多边形):
⑴由一种图形完成的条件是形状大小都一致: 如 ;
⑵由两种正多边形完成的条件是边长之间有整倍数关系:如 ,可以用二元一次方程 求得各需要多少个图形;
⑶由三种正多边形完成的条件是边长之间有整倍数关系如 ; 若每种只用一个则边数之间满足 。
达标练习:
一、填空题
1.如果三角形的一个角等于其它两个角的差,则这个三角形是______三角形.
2.已知△ABC中,AD⊥BC于D,AE为∠A的平分线,且∠B=35°,∠C=65°,则∠DAE的度数为_____ .
3.三角形中最大的内角不能小于_____,两个外角的和必大于_____ .
4.三角形ABC中,∠A=40°,顶点C处的外角为110°,那么∠B=_____ .
5.锐角三角形任意两锐角的和必大于_____.
6.三角形的三个外角都大于和它相邻的内角,则这个三角形为 ___ __ 三角形.
7.在三角形ABC中,已知∠A=80°,∠B=50°,那么∠C的度数是 .
8.已知∠A=∠B=3∠C,则∠A= .
9.已知,如图7-1,∠ACD=130°,∠A=∠B,那么∠A的度数是 .
10.如图7-2,根据图形填空:
(1)AD是△ABC中∠BAC的角平分线,则∠ =∠ =∠ .
(2)AE是△ABC中线,则 = = .
(3)AF是△ABC的高,则∠ =∠ =90°.
11.如图7-3所示,图中有 个三角形, 个直角三角形.
12.在四边形的四个外角中,最多有 个钝角,最多有 个锐角,最多有 个直角.
13.四边形ABCD中,若∠A+∠B=∠C+∠D,若∠C=2∠D,则∠C= .
14.一个多边形的每个外角都为30°,则这个多边形的边数为 ;一个多边形的每个内角都为135°,则这个多边形的边数为 .
15.某足球场需铺设草皮,现有正三角形、正四边形、正五边形、正六边形、正八边形、正十边形6种形状的草皮,请你帮助工人师傅选择两种草皮来铺设足球场,可供选择的两种组合是 .
16.若一个n边形的边数增加一倍,则内角和将 .
17.在一个顶点处,若此正n边形的内角和为 ,则此正多边形可以铺满地面.
18.如图7-4,BC⊥ED于O,∠A=27°,∠D=20°,则∠B= ,∠ACB= .
(21题图) (22题图)
19.如图7-5,由平面上五个点A、B、C、D、E连结而成,则∠A+∠B+∠C+∠D+∠E= .
20.以长度为5cm、7cm、9cm、13cm的线段中的三条为边,能够组成三角形的情况有 种,分别是 .
21. 如图,在三角形ABC中,AD⊥BC,BE⊥AC,CF⊥AB,BC=16,AD=3,BE=4,CF=6,则三角形ABC的周长是 。
22、如图,已知三角形ABC的三个内角平分线交于点I,IH⊥BC于H,∠CIH和∠BID的大小关系是 .
23、如果a ,b ,c为三角形的三边,且,则这个三角形是
三角形。
24、一个多边形的每一个外角都等于30°,这个多边形的边数是 ,它的内角和是 。
二、选择题
1.已知三角形ABC的三个内角满足关系∠B+∠C=3∠A,则此三角形( ).
A.一定有一个内角为45° B.一定有一个内角为60°
C.一定是直角三角形 D.一定是钝角三角形
2.如果一个三角形的三个外角之比为2:3:4,则与之对应的三个内角度数之比为( ).
A.4:3:2 B.3:2:4 C.5:3:1 D.3:1:5
3.三角形中至少有一个内角大于或等于( ). A.45° B.55° C.60° D.65°
4.如图7-6,下列说法中错误的是( ).
A.∠1不是三角形ABC的外角 B.∠B<∠1+∠2
C.∠ACD是三角形ABC的外角 D.∠ACD>∠A+∠B
5.如图7-7,C在AB的延长线上,CE⊥AF于E,交FB于D,
若∠F=40°,∠C=20°,则∠FBA的度数为( ).
A.50° B.60° C.70° D.80°
6.下列叙述中错误的一项是( ).
A.三角形的中线、角平分线、高都是线段.
B.三角形的三条高线中至少存在一条在三角形内部.
C.只有一条高在三角形内部的三角形一定是钝角三角形.
D.三角形的三条角平分线都在三角形内部.
7.下列长度的三条线段中,能组成三角形的是( ).
A.1,5,7 B.3,4,7 C.7,4,1 D.5,5,5
8.如果三角形的两边长为3和5,那么第三边长可以是下面的( ).
A.1 B.9 C.3 D.10
9.三条线段a=5,b=3,c的值为整数,由a、b、c为边可组成三角形( ).
A.1个 B.3个 C.5个 D.无数个
10.四边形的四个内角可以都是( ).
A.锐角 B.直角 C.钝角 D.以上答案都不对
11.一个五边形有三个角是直角,另两个角都等于n,则n的值为( ).
A.108° B.125° C.135° D.150°
12.多边形每一个内角都等于150°,则从此多边形一个顶点发出的对角线有( ).
A.7条 B.8条 C.9条 D.10条
13.如图7-9,三角形ABC中,D为BC上的一点,且S△ABD=S△ADC,则AD为( ).
A.高 B.角平分线 C.中线 D.不能确定
14.如图7-10,已知∠1=∠2,则AH必为三角形ABC的( ).
A.角平分线 B.中线 C.一角的平分线 D.角平分线所在射线
15.现有长度分别为2cm、4cm、6cm、8cm的木棒,从中任取三根,能组成三角形的个数为( ). A. 1 B. 2 C. 3 D. 4
16.如图7-11,三角形ABC中,AD平分∠BAC,EG⊥AD,且分别交AB、AD、AC及BC的延长线于点E、H、F、G,下列四个式子中正确的是( )
17.如图,凸六边形ABCDEF的六个角都是120°,边长AB=2cm,BC=8cm,CD=11cm,DE=6cm,这个六边形的周长是 。
18.如果多边形的内角和是外角和的k倍,那么这个多边形的边数是( ).
A.k B.2k+1 C.2k+2 D.2k-2
19.如图所示,在长为5cm,宽为3cm的长方形内部有一平行四边形,
则平行四边形的面积为( ). A.7cm2 B.8cm2 C.9cm2 D.10cm2
20、如图所示,在△ABC中,D在AC上,连结BD,且∠ABC=∠C=∠1,∠A=∠3,则∠A 的度数为( ). A.30° B.36° C.45° D.72°
21、.如图所示,已知△ABC为直角三角形,∠C=90,若烟图中虚线剪去∠C,则∠1+∠2 等于( ) A、90° B、135° C、270° D、315°
图7-1
图7-2 图7-3
图7-4 图7-5
图7-6
图7-7
图7-9 图7-10
图7-11
1、三角形的定义:
不在 上的三条线段 连接而成的平面图形。
其表示方法是符号“△”后接着三个顶点字母。三角形是边数最少的多边形。
2、三角形的有关重要线段:
⑴三角形的三边:三角形的两边之和 第三边;两边之差 第三边;
△ABC的三边a、b、c中已知a、b,求c的取值范围是: <c< ;
⑵三角形的高线、中线、角平分线:①三线都经过顶点;②都是 ;③除直角三角形的两条高线在三角形的两条 边上,钝角三角形的两条高线在三角形 ,其他各线均在形内;④三条中线、三条角平分线、三条高线均交于一点:锐角三角形的高交于三角形 一点,直角三角形的高交于三角形的 点,钝角三角形的高的延长线交于三角形 一点。⑤三角形的一条中线把三角形分成两个 相等的小三角形;三条中线交点把每条中线分成 ∶ 两部分;有中线就有线段的倍分关系;⑥三角形的角平分线交点到三角形三边距离 ;有角平分线就有角的倍分关系;⑦有高就有 度的角,三角形的各边与这边上的高的乘积相等,据此可以建立方程解题:如图4中有:AB·CF=BC· = · ;⑧要能用几何语言表达三角形的三线。
3、三角形的稳定性的应用举例: ,四边形的不稳定性的应用举例: 。
4、三角形有关的角:⑴内角和等于 ;要能用推理得出结论;
⑵外角:是三角形的一边与另一边的 的夹角,外角和等于 ;
⑶三角形的一个外角等于 ,大于 ;三角形的外角与与之相邻的内角互为 ;
⑷三角形的两条内角平分线的夹角等于 与第三个角的 的和,如图5,P是△ABC的两条角平分线的交点,且∠A=α,则∠P= ;三角形的一条内角平分线和一条外角平分线的夹角等于第三个角的 ,如图6,P是△ABC的内角平分线和外角平分线的交点,且∠A=α,则∠P= ;三角形的两条外角平分线的夹角等于 与第三个角的 的差,如图7,P是△ABC的两条外角平分线的交点,且∠A=α,则∠P= ;
5、多边形:
⑴定义: 的几条线段 连接而成的平面图形;
叫正多边形;
⑵对角线:多边形中不相邻的两个顶点之间的连线。n边形从一个顶点出发有 对角线,这些对角线把n边形分成了 三角形,n边形共有 条对角线;
⑶n边形的内角和等于 ,正n边形的内角和还可以用 × 求得;
所以可以据此建立方程求边数;要能用三种割分多边形的方法求得多边形的内角和公式;
⑷多边形的外角和都等于 ,正n边形的每个内角度数可以通过180°-360°÷n求得;
⑸多边形的内角中最多有 个锐角,即外角中最多有 个钝角;要知道理由。
⑹一笔画图形各个顶角之和的求法规律:若一个一笔画图形由n条线段组成,则其各个顶角之和等于 ;如图8的图形由6条线段构成,则∠A+∠B+∠C+∠D+∠E+∠F= ;要与多边形的内角和区别开来;
⑺若两个角的两边分别平行(或垂直),那么这两个角的大小关系是:
或 。
6、镶嵌:顶点之处各角之和为 (条件之一),以下举例(主要是正多边形):
⑴由一种图形完成的条件是形状大小都一致: 如 ;
⑵由两种正多边形完成的条件是边长之间有整倍数关系:如 ,可以用二元一次方程 求得各需要多少个图形;
⑶由三种正多边形完成的条件是边长之间有整倍数关系如 ; 若每种只用一个则边数之间满足 。
达标练习:
一、填空题
1.如果三角形的一个角等于其它两个角的差,则这个三角形是______三角形.
2.已知△ABC中,AD⊥BC于D,AE为∠A的平分线,且∠B=35°,∠C=65°,则∠DAE的度数为_____ .
3.三角形中最大的内角不能小于_____,两个外角的和必大于_____ .
4.三角形ABC中,∠A=40°,顶点C处的外角为110°,那么∠B=_____ .
5.锐角三角形任意两锐角的和必大于_____.
6.三角形的三个外角都大于和它相邻的内角,则这个三角形为 ___ __ 三角形.
7.在三角形ABC中,已知∠A=80°,∠B=50°,那么∠C的度数是 .
8.已知∠A=∠B=3∠C,则∠A= .
9.已知,如图7-1,∠ACD=130°,∠A=∠B,那么∠A的度数是 .
10.如图7-2,根据图形填空:
(1)AD是△ABC中∠BAC的角平分线,则∠ =∠ =∠ .
(2)AE是△ABC中线,则 = = .
(3)AF是△ABC的高,则∠ =∠ =90°.
11.如图7-3所示,图中有 个三角形, 个直角三角形.
12.在四边形的四个外角中,最多有 个钝角,最多有 个锐角,最多有 个直角.
13.四边形ABCD中,若∠A+∠B=∠C+∠D,若∠C=2∠D,则∠C= .
14.一个多边形的每个外角都为30°,则这个多边形的边数为 ;一个多边形的每个内角都为135°,则这个多边形的边数为 .
15.某足球场需铺设草皮,现有正三角形、正四边形、正五边形、正六边形、正八边形、正十边形6种形状的草皮,请你帮助工人师傅选择两种草皮来铺设足球场,可供选择的两种组合是 .
16.若一个n边形的边数增加一倍,则内角和将 .
17.在一个顶点处,若此正n边形的内角和为 ,则此正多边形可以铺满地面.
18.如图7-4,BC⊥ED于O,∠A=27°,∠D=20°,则∠B= ,∠ACB= .
(21题图) (22题图)
19.如图7-5,由平面上五个点A、B、C、D、E连结而成,则∠A+∠B+∠C+∠D+∠E= .
20.以长度为5cm、7cm、9cm、13cm的线段中的三条为边,能够组成三角形的情况有 种,分别是 .
21. 如图,在三角形ABC中,AD⊥BC,BE⊥AC,CF⊥AB,BC=16,AD=3,BE=4,CF=6,则三角形ABC的周长是 。
22、如图,已知三角形ABC的三个内角平分线交于点I,IH⊥BC于H,∠CIH和∠BID的大小关系是 .
23、如果a ,b ,c为三角形的三边,且,则这个三角形是
三角形。
24、一个多边形的每一个外角都等于30°,这个多边形的边数是 ,它的内角和是 。
二、选择题
1.已知三角形ABC的三个内角满足关系∠B+∠C=3∠A,则此三角形( ).
A.一定有一个内角为45° B.一定有一个内角为60°
C.一定是直角三角形 D.一定是钝角三角形
2.如果一个三角形的三个外角之比为2:3:4,则与之对应的三个内角度数之比为( ).
A.4:3:2 B.3:2:4 C.5:3:1 D.3:1:5
3.三角形中至少有一个内角大于或等于( ). A.45° B.55° C.60° D.65°
4.如图7-6,下列说法中错误的是( ).
A.∠1不是三角形ABC的外角 B.∠B<∠1+∠2
C.∠ACD是三角形ABC的外角 D.∠ACD>∠A+∠B
5.如图7-7,C在AB的延长线上,CE⊥AF于E,交FB于D,
若∠F=40°,∠C=20°,则∠FBA的度数为( ).
A.50° B.60° C.70° D.80°
6.下列叙述中错误的一项是( ).
A.三角形的中线、角平分线、高都是线段.
B.三角形的三条高线中至少存在一条在三角形内部.
C.只有一条高在三角形内部的三角形一定是钝角三角形.
D.三角形的三条角平分线都在三角形内部.
7.下列长度的三条线段中,能组成三角形的是( ).
A.1,5,7 B.3,4,7 C.7,4,1 D.5,5,5
8.如果三角形的两边长为3和5,那么第三边长可以是下面的( ).
A.1 B.9 C.3 D.10
9.三条线段a=5,b=3,c的值为整数,由a、b、c为边可组成三角形( ).
A.1个 B.3个 C.5个 D.无数个
10.四边形的四个内角可以都是( ).
A.锐角 B.直角 C.钝角 D.以上答案都不对
11.一个五边形有三个角是直角,另两个角都等于n,则n的值为( ).
A.108° B.125° C.135° D.150°
12.多边形每一个内角都等于150°,则从此多边形一个顶点发出的对角线有( ).
A.7条 B.8条 C.9条 D.10条
13.如图7-9,三角形ABC中,D为BC上的一点,且S△ABD=S△ADC,则AD为( ).
A.高 B.角平分线 C.中线 D.不能确定
14.如图7-10,已知∠1=∠2,则AH必为三角形ABC的( ).
A.角平分线 B.中线 C.一角的平分线 D.角平分线所在射线
15.现有长度分别为2cm、4cm、6cm、8cm的木棒,从中任取三根,能组成三角形的个数为( ). A. 1 B. 2 C. 3 D. 4
16.如图7-11,三角形ABC中,AD平分∠BAC,EG⊥AD,且分别交AB、AD、AC及BC的延长线于点E、H、F、G,下列四个式子中正确的是( )
17.如图,凸六边形ABCDEF的六个角都是120°,边长AB=2cm,BC=8cm,CD=11cm,DE=6cm,这个六边形的周长是 。
18.如果多边形的内角和是外角和的k倍,那么这个多边形的边数是( ).
A.k B.2k+1 C.2k+2 D.2k-2
19.如图所示,在长为5cm,宽为3cm的长方形内部有一平行四边形,
则平行四边形的面积为( ). A.7cm2 B.8cm2 C.9cm2 D.10cm2
20、如图所示,在△ABC中,D在AC上,连结BD,且∠ABC=∠C=∠1,∠A=∠3,则∠A 的度数为( ). A.30° B.36° C.45° D.72°
21、.如图所示,已知△ABC为直角三角形,∠C=90,若烟图中虚线剪去∠C,则∠1+∠2 等于( ) A、90° B、135° C、270° D、315°
图7-1
图7-2 图7-3
图7-4 图7-5
图7-6
图7-7
图7-9 图7-10
图7-11
