鲁教版(五四制)七年级下册8 平行线的有关证明 课件((共19张PPT))
文档属性
| 名称 | 鲁教版(五四制)七年级下册8 平行线的有关证明 课件((共19张PPT)) |  | |
| 格式 | pptx | ||
| 文件大小 | 322.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-17 17:34:40 | ||
图片预览






文档简介
(共19张PPT)
第八章 平行线的有关证明
复习课件
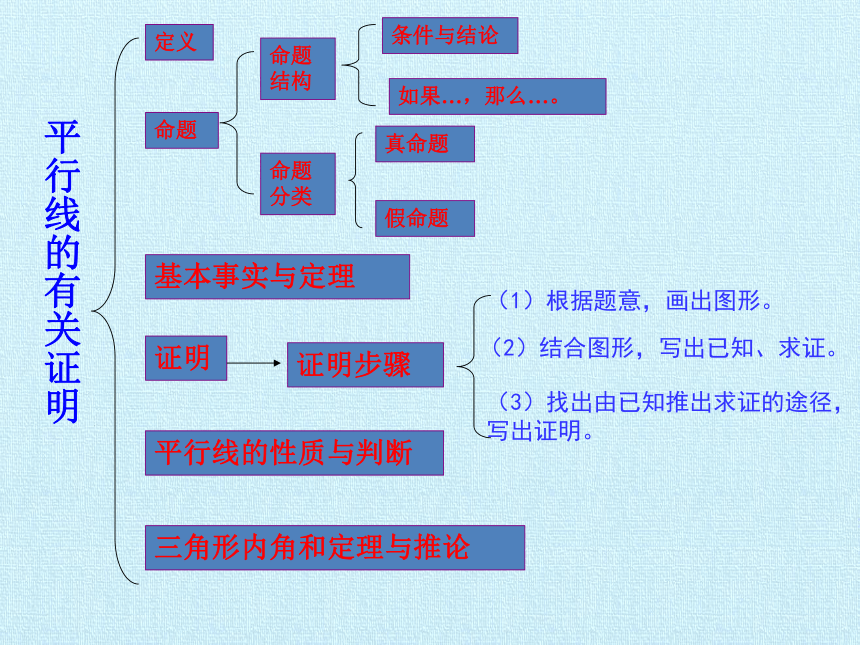
定义
平行线的有关证明
平行线的性质与判断
证明
条件与结论
证明步骤
命题
真命题
假命题
基本事实与定理
三角形内角和定理与推论
命题结构
命题
分类
如果…,那么…。
(1)根据题意,画出图形。
(2)结合图形,写出已知、求证。
(3)找出由已知推出求证的途径,写出证明。
要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具备命题的结论,这种例子称为反例。
定义:用来说明一个名词含义的语句叫做定义。
命题:判断一件事情的句子,叫做命题。
知识回顾
每个命题都由条件和结论两部分组成。条件是已知事项,结论是由已事项推断出的事项。
一般地,命题可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的部分是结论。
正确的命题称为真命题,不正确的的命题称为假命题。
1.指出下列命题的条件和结论:
(1)若a∥b,b∥c,则a∥c。
(2)如果两个角相等,那么这两个角是对顶角。
(3)同一个角的补角相等。
2.把下列命题改写成“如果……,那么……”的形式:
(1)平行于同一直线的两条直线平行。
(2)同角的余角相等。
(3)绝对值相等的两个数一定相等。
3.判断下列命题是真命题,还是假命题;如果是假命题,举一个反例。
(1)若a2>b2,则a>b。
(2)同位角相等,两直线平行。
(3)一个角的余角小于这个角。
练习
本书把下列基本事实作为证明的依据
1.两点确定一条直线。
2.两点之间线段最短。
3.同一平面内,过一点有且只有一条直线与已知直线垂直。
4.同位角相等,两直线平行。
5.过直线外一点,有且只有一条直线与已知直线平行。
6.两边及其夹角分别相等的两个三角形全等。
7.两角及其夹边分别相等的两个三角形全等。
8.三边分别相等的两个三角形全等。
平行线的判定
基本事实:
同位角相等,两直线平行。
∵∠1=∠2
∴a∥b
判定定理1:
内错角相等,两直线平行。
∵∠1=∠2
∴a∥b
判定定理2:
同旁内角互补,两直线平行。
∵∠1+∠2=1800
∴a∥b
性质定理1:
两直线平行,同位角相等。
∵a∥b,∴∠1=∠2。
性质定理2:
两直线平行,内错角相等。
∵a∥b,∴∠1=∠2。
性质定理3:
两直线平行,同旁内角互补。
∵a∥b,∴∠1+∠2=1800。
平行线的性质
三角形内角和定理
三角形内角和定理三角形三个内角的和等于1800。
△ABC中,∠A+∠B+∠C=1800。
∠A+∠B+∠C=1800的几种变形:
∠A=1800–(∠B+∠C)。
∠B=1800–(∠A+∠C)。
∠C=1800–(∠A+∠B)。
∠A+∠B=1800-∠C。
∠B+∠C=1800-∠A。
∠A+∠C=1800-∠B。
这里的结论,以后可以直接运用。
A
B
C
知识回顾
证明三角形的内角和定理的基本思路是:通过作平行线把分散的三个内角集中到一个顶点处,从而构成了一个平角。而作平行线是将角“搬”在一起的基本途径。
图1
图2
图3
A
B
C
C
B
A
A
B
B
C
C
B
A
B
A
B
C
P
Q
D
E
1
2
关注三角形的外角
三角形内角和定理的推论:
推论1:三角形的一个外角等于和它不相邻的两个内角的和。
推论2:三角形的一个外角大于任何一个和它不相邻的内角。
△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3。
A
B
C
D
1
2
3
4
这个结论以后可以直接运用。
知识回顾
当堂训练
1.三角形的每个外角都大于相邻的内角,则它的形状是_________,三角形的一个外角小于相邻的一个人内角,则它的形状是_________,三角形的一个外角等于相邻的一个内角,则它的形状为_________。
锐角三角形
钝角三角形
直角三角形
3.如图,小明在折纸活动中制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,A与A'重合,
若∠A=75°,
则∠1+∠2=______。
4.如图,∠A+∠B+∠C+
∠D+∠E的度数为_____。
150°
180°
5.如图,∠1+∠2=180°,∠A=∠C,AD平分∠BDF。
求证:BC平分∠DBE。
证明:∵∠1+∠2=180°,
∠BDC+∠2=180°
∴∠1=∠BDC
∴AE∥FC
∴∠EBC=∠C
A
E
C
D
B
F
1
2
∵∠A=∠C
∴∠EBC=∠A
∴AD∥BC
∴∠ADB=∠CBD
∠ADF=∠C
∵AD平分∠BDF
∴∠ADF=∠ADB
∴∠CBD=∠C
∴∠CBD=∠EBC
∴BC平分∠DBE
6.如图所示,在△ABC中,∠CAB=52°,∠1=∠2=∠3。
(1)求∠EDF的度数;(2)猜想△DEF的各内角与△ABC的各内角有什么关系,并说明理由。
解:(1)∵∠1=∠2
∠EDF=∠CAD+∠1
∴∠EDF=∠CAD+∠2
=∠CAB=52°
D
1
2
A
B
F
3
C
E
(2)△DEF与△ABC的各内角
分别相等。理由:
由(1)可知:∠EDF=∠CAB
∵∠1=∠2=∠3,∠DEF=∠2+∠FBA
∴∠DEF=∠3+∠FBA=∠ABC
同理:∠DFE=∠ACB
∴△DEF与△ABC的各内角分别相等。
7.平面内的两条直线有相交和平行两种位置关系。
(1)如图a,AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D。将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有和数量关系?请证明你的结论。
解:(1)不成立,结论是∠BPD=∠B+∠D。
延长BP交CD于点E。
∵AB∥CD∴∠B=∠BED
∵∠BPD=∠BED+∠D
∴∠BPD=∠B+∠D
E
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明)
结论是∠BPD=∠BQD+∠B+∠D。
谢 谢
第八章 平行线的有关证明
复习课件
定义
平行线的有关证明
平行线的性质与判断
证明
条件与结论
证明步骤
命题
真命题
假命题
基本事实与定理
三角形内角和定理与推论
命题结构
命题
分类
如果…,那么…。
(1)根据题意,画出图形。
(2)结合图形,写出已知、求证。
(3)找出由已知推出求证的途径,写出证明。
要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具备命题的结论,这种例子称为反例。
定义:用来说明一个名词含义的语句叫做定义。
命题:判断一件事情的句子,叫做命题。
知识回顾
每个命题都由条件和结论两部分组成。条件是已知事项,结论是由已事项推断出的事项。
一般地,命题可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的部分是结论。
正确的命题称为真命题,不正确的的命题称为假命题。
1.指出下列命题的条件和结论:
(1)若a∥b,b∥c,则a∥c。
(2)如果两个角相等,那么这两个角是对顶角。
(3)同一个角的补角相等。
2.把下列命题改写成“如果……,那么……”的形式:
(1)平行于同一直线的两条直线平行。
(2)同角的余角相等。
(3)绝对值相等的两个数一定相等。
3.判断下列命题是真命题,还是假命题;如果是假命题,举一个反例。
(1)若a2>b2,则a>b。
(2)同位角相等,两直线平行。
(3)一个角的余角小于这个角。
练习
本书把下列基本事实作为证明的依据
1.两点确定一条直线。
2.两点之间线段最短。
3.同一平面内,过一点有且只有一条直线与已知直线垂直。
4.同位角相等,两直线平行。
5.过直线外一点,有且只有一条直线与已知直线平行。
6.两边及其夹角分别相等的两个三角形全等。
7.两角及其夹边分别相等的两个三角形全等。
8.三边分别相等的两个三角形全等。
平行线的判定
基本事实:
同位角相等,两直线平行。
∵∠1=∠2
∴a∥b
判定定理1:
内错角相等,两直线平行。
∵∠1=∠2
∴a∥b
判定定理2:
同旁内角互补,两直线平行。
∵∠1+∠2=1800
∴a∥b
性质定理1:
两直线平行,同位角相等。
∵a∥b,∴∠1=∠2。
性质定理2:
两直线平行,内错角相等。
∵a∥b,∴∠1=∠2。
性质定理3:
两直线平行,同旁内角互补。
∵a∥b,∴∠1+∠2=1800。
平行线的性质
三角形内角和定理
三角形内角和定理三角形三个内角的和等于1800。
△ABC中,∠A+∠B+∠C=1800。
∠A+∠B+∠C=1800的几种变形:
∠A=1800–(∠B+∠C)。
∠B=1800–(∠A+∠C)。
∠C=1800–(∠A+∠B)。
∠A+∠B=1800-∠C。
∠B+∠C=1800-∠A。
∠A+∠C=1800-∠B。
这里的结论,以后可以直接运用。
A
B
C
知识回顾
证明三角形的内角和定理的基本思路是:通过作平行线把分散的三个内角集中到一个顶点处,从而构成了一个平角。而作平行线是将角“搬”在一起的基本途径。
图1
图2
图3
A
B
C
C
B
A
A
B
B
C
C
B
A
B
A
B
C
P
Q
D
E
1
2
关注三角形的外角
三角形内角和定理的推论:
推论1:三角形的一个外角等于和它不相邻的两个内角的和。
推论2:三角形的一个外角大于任何一个和它不相邻的内角。
△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3。
A
B
C
D
1
2
3
4
这个结论以后可以直接运用。
知识回顾
当堂训练
1.三角形的每个外角都大于相邻的内角,则它的形状是_________,三角形的一个外角小于相邻的一个人内角,则它的形状是_________,三角形的一个外角等于相邻的一个内角,则它的形状为_________。
锐角三角形
钝角三角形
直角三角形
3.如图,小明在折纸活动中制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,A与A'重合,
若∠A=75°,
则∠1+∠2=______。
4.如图,∠A+∠B+∠C+
∠D+∠E的度数为_____。
150°
180°
5.如图,∠1+∠2=180°,∠A=∠C,AD平分∠BDF。
求证:BC平分∠DBE。
证明:∵∠1+∠2=180°,
∠BDC+∠2=180°
∴∠1=∠BDC
∴AE∥FC
∴∠EBC=∠C
A
E
C
D
B
F
1
2
∵∠A=∠C
∴∠EBC=∠A
∴AD∥BC
∴∠ADB=∠CBD
∠ADF=∠C
∵AD平分∠BDF
∴∠ADF=∠ADB
∴∠CBD=∠C
∴∠CBD=∠EBC
∴BC平分∠DBE
6.如图所示,在△ABC中,∠CAB=52°,∠1=∠2=∠3。
(1)求∠EDF的度数;(2)猜想△DEF的各内角与△ABC的各内角有什么关系,并说明理由。
解:(1)∵∠1=∠2
∠EDF=∠CAD+∠1
∴∠EDF=∠CAD+∠2
=∠CAB=52°
D
1
2
A
B
F
3
C
E
(2)△DEF与△ABC的各内角
分别相等。理由:
由(1)可知:∠EDF=∠CAB
∵∠1=∠2=∠3,∠DEF=∠2+∠FBA
∴∠DEF=∠3+∠FBA=∠ABC
同理:∠DFE=∠ACB
∴△DEF与△ABC的各内角分别相等。
7.平面内的两条直线有相交和平行两种位置关系。
(1)如图a,AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D。将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有和数量关系?请证明你的结论。
解:(1)不成立,结论是∠BPD=∠B+∠D。
延长BP交CD于点E。
∵AB∥CD∴∠B=∠BED
∵∠BPD=∠BED+∠D
∴∠BPD=∠B+∠D
E
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明)
结论是∠BPD=∠BQD+∠B+∠D。
谢 谢
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
