余弦函数的图象和性质[上学期]
图片预览






文档简介
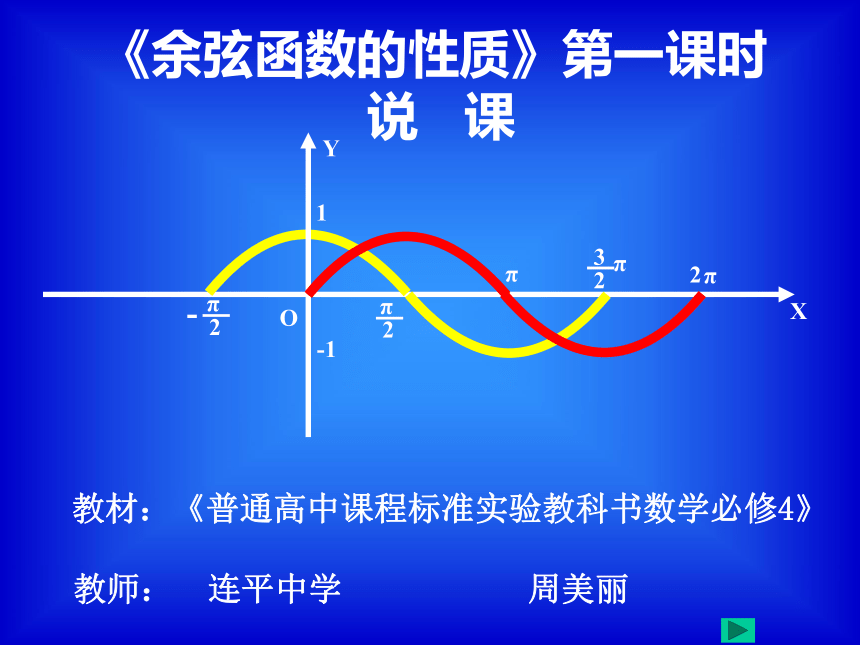
课件29张PPT。《余弦函数的性质》第一课时
说 课教材:《普通高中课程标准实验教科书数学必修4》教师: 连平中学 周美丽 πXOY1-1π2π一、教材分析
二、学生分析
三、教法学法分析
四、过程分析
五、评价分析二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(一)地位与作用 一、教材分析 余弦函数的性质是北师大版必修4第一章的内容,正弦、余弦函数的图像和性质是三角函数内容里的重点内容,也是高考热点考察的内容之一。通过本节课的学习,不仅可以培养学生的观察能力,分析问题、解决问题的能力,而且渗透了重要的数学思想方法比如:类比、分类讨论、数形结合等思想方法,为以后的学习打下铺垫。
(二)教学目标 :二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(1)知识目标:?类比正弦函数的性质,观察正弦、余弦函数图像得到余弦函数的性质,并掌握性质的应用。
(2)能力目标: 培养学生自主探索与合作学习的能力,同时也培养学生应用类比、分类讨论、化归以及数形结合等数学思想方法在解决问题中的应用能力;(3)情感目标: 让学生亲身经历数学的研究过程,体现发现的激情,感受数学的魅力;使学生在学习活动中获得成功感,从而培养学生热爱数学、积极学习数学、应用数学的热情。
重点:从余弦函数的图像得到余弦函数的性质 (三)教学重点与难点突破难点的方法:
应该对这些性质的应用进行多层次练习,通过循环反复、螺旋递进方式进行练习,使学生在练习中掌握余弦函数的性质及应用。
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析难点:余弦函数性质的应用
(一)知识结构(二)能力方面二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(三)情感方面学生在必修1学习了函数的有关概念,以及几个中学阶段的初等函数,在本章书的第一节介绍了周期函数的概念,正弦函数的图像和性质,所以已经具有了这节课的预备知识。
具有一定的分析问题,解决问题的能力,函数思想和数形结合思想已经略有了解,在教师的指导下能力目标不难达到。高一学生参与意识、自主探究意识逐渐增强,能够对认识有冲突的、能够表现自身价值的学习素材比较感兴趣。
三、教法学法分析(一)教学方法:引导发现教学法
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析 为了让学生有发现创造的机会,有获得知识的成功的体验,为了立足于学生思维发展,着力于知识的建构,就必须让学生有观察、动手、表达、交流、表现的机会,采用引导发现法,可激发学生学习的积极性和创造性,分享到探索知识的方法和乐趣,使数学教学成为再发现,再创造的过程。
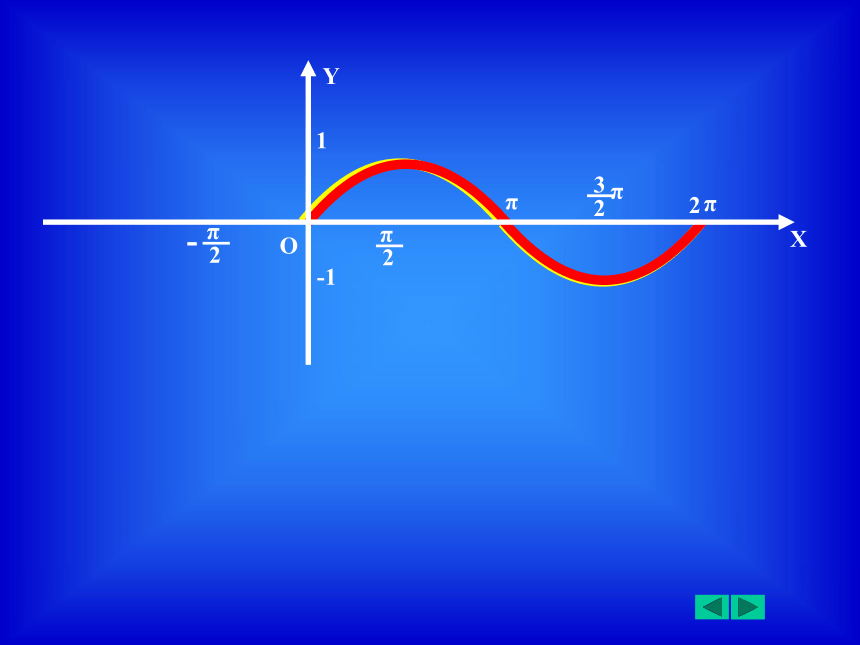
(一)学法指导:问题探究法根据“倡导积极主动、勇于探索、师生互动”的基本理念,根据教材内容特点以及学生的知识、能力、情感等因素从而把学法定为问题探究法。(一)引入新课 ——揭示课题 四、过程分析二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(2)在让学生观察它们的图像,自主探索两个图像之间的关系,得出两个图像位置位置关系的结论。(1)让学生画出正弦函数、余弦函数的图像;设计意图:通过画出图像,研究图像间的关系,可以培养学生的自主探索、发现问题的能力。
πππππππ结论:余弦函数的图像可由正弦函数的图像向左平移 个单位得到。
(二)余弦函数的性质探讨 (1)从两个图像间的位置关系,小组合作讨论,从两个方面探讨:与位置无关的性质有哪些,与位置有关的性质又有哪些。
设计意图: 让学生小组合作讨论学习,充分体现“新课程、新理念”的思想。
π类比正弦函数的性质得到:定义域、值域、最值、周期性(2)师生互动:
一起回顾正弦函数的性质,类比其性质,得到跟位置无关的性质;再结合余弦函数的图像,再得到跟位置有关的性质。并对比正弦、余弦函数的性质的异同。
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析设计意图:通过学生观察、类比、小组合作讨论得出余弦函数的性质,同时让学生自主发现,类比学习,达到了自主探究学习的目的。也充分体现师生互动的教学模式。
π学生再次讨论得到跟位置有关的性质:单调性、奇偶性、对称性、取得最值时x的集合
(三)余弦函数性质的应用
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析1、课本例题探讨
设计意图:
立足于课本,让学生熟练掌握函数图像常用的画法—五点法,并通过图像能够观察得到函数的性质。
2、课本思考交流:
设计意图:
有意识的训练学生借助图像进行分析解决问题的能力,强调图像的作用,渗透数形结合的数学思想方法,并且为下面求函数的定义域打好基础。 3、典型例题剖析: 例1:求下列函数的定义域 组A. (1)(2)组B.(1)(2)二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析 (2)通过两组题,着重强调了求函数定义域的关键是转化为解三角不等式,重点突出了图像在解题中的作用,让学生掌握数形结合的思想方法,从而达到了突破本节课的一个难点。
设计意图:
为了满足优生吃不饱的现象,我对求函数的定义域又作了一个课后展望:
求 函数的定义域,作为课后思考。
?
(1)为了掌握求函数的定义域的方法,我设计了例1,考虑到学生知识水平的差异性,我安排了A、B两组题,意在让学生根据自己的基础选用适合自己的题组,通过思考每位同学都能自主地完成,从而能让学生都能够体验到,获得知识时的一种成功感、喜悦感,而且又能够充分调动每位学生的学习的热情,体现了师生互动的课堂效果。
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(加强条件 ) 变式: 例2:求下列函数的值域: (1)二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析设计意图:
(1)到掌握求函数值域方法,我安排了例2,然后对条件进行加强和变式,让题目由浅入深,螺旋递进,使学生的知识逐渐深化。
(2)对于变式,再让学生小组合作讨论,后针对学生出现的各种情况,讨论a的符号对值域的影响,从而培养学生初步分类讨论的思想,有效激励学生探讨问题,掌握知识的方法,同时进一步体现教材的再度开发。
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(2)引申:设计意图:
①使学生把三角函数的内容跟二次函数的内容紧密的联系起来,能够把三角函数求值域转化为熟悉的二次函数求值域,设计了一道有关三角的二次函数求值域的题型。让学生体验知识之间的紧密联系。
②对于如何解这类型的题目时,我特别设置错误的结果,有意让学生从错误中深刻掌握,换元后的变量的有界性,我做了特别的强调。
③为了让学生进一步掌握这一类型的方法,我考虑对该题引申为带有参数,让学生作为课后探讨的内容,这也是再次用到分类讨论思想,进一步培养学生分析问题、讨论问题的完整性、周密性。
?
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(四)作业
(五)小结:
本节课由学生进行小结,提出掌握了哪些内容,还有哪些有疑惑。 二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析五、评价分析 这是我对这一节课的大致设想,欢迎各位领导、老师多提宝贵意见。
?
谢谢!!
说 课教材:《普通高中课程标准实验教科书数学必修4》教师: 连平中学 周美丽 πXOY1-1π2π一、教材分析
二、学生分析
三、教法学法分析
四、过程分析
五、评价分析二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(一)地位与作用 一、教材分析 余弦函数的性质是北师大版必修4第一章的内容,正弦、余弦函数的图像和性质是三角函数内容里的重点内容,也是高考热点考察的内容之一。通过本节课的学习,不仅可以培养学生的观察能力,分析问题、解决问题的能力,而且渗透了重要的数学思想方法比如:类比、分类讨论、数形结合等思想方法,为以后的学习打下铺垫。
(二)教学目标 :二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(1)知识目标:?类比正弦函数的性质,观察正弦、余弦函数图像得到余弦函数的性质,并掌握性质的应用。
(2)能力目标: 培养学生自主探索与合作学习的能力,同时也培养学生应用类比、分类讨论、化归以及数形结合等数学思想方法在解决问题中的应用能力;(3)情感目标: 让学生亲身经历数学的研究过程,体现发现的激情,感受数学的魅力;使学生在学习活动中获得成功感,从而培养学生热爱数学、积极学习数学、应用数学的热情。
重点:从余弦函数的图像得到余弦函数的性质 (三)教学重点与难点突破难点的方法:
应该对这些性质的应用进行多层次练习,通过循环反复、螺旋递进方式进行练习,使学生在练习中掌握余弦函数的性质及应用。
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析难点:余弦函数性质的应用
(一)知识结构(二)能力方面二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(三)情感方面学生在必修1学习了函数的有关概念,以及几个中学阶段的初等函数,在本章书的第一节介绍了周期函数的概念,正弦函数的图像和性质,所以已经具有了这节课的预备知识。
具有一定的分析问题,解决问题的能力,函数思想和数形结合思想已经略有了解,在教师的指导下能力目标不难达到。高一学生参与意识、自主探究意识逐渐增强,能够对认识有冲突的、能够表现自身价值的学习素材比较感兴趣。
三、教法学法分析(一)教学方法:引导发现教学法
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析 为了让学生有发现创造的机会,有获得知识的成功的体验,为了立足于学生思维发展,着力于知识的建构,就必须让学生有观察、动手、表达、交流、表现的机会,采用引导发现法,可激发学生学习的积极性和创造性,分享到探索知识的方法和乐趣,使数学教学成为再发现,再创造的过程。
(一)学法指导:问题探究法根据“倡导积极主动、勇于探索、师生互动”的基本理念,根据教材内容特点以及学生的知识、能力、情感等因素从而把学法定为问题探究法。(一)引入新课 ——揭示课题 四、过程分析二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(2)在让学生观察它们的图像,自主探索两个图像之间的关系,得出两个图像位置位置关系的结论。(1)让学生画出正弦函数、余弦函数的图像;设计意图:通过画出图像,研究图像间的关系,可以培养学生的自主探索、发现问题的能力。
πππππππ结论:余弦函数的图像可由正弦函数的图像向左平移 个单位得到。
(二)余弦函数的性质探讨 (1)从两个图像间的位置关系,小组合作讨论,从两个方面探讨:与位置无关的性质有哪些,与位置有关的性质又有哪些。
设计意图: 让学生小组合作讨论学习,充分体现“新课程、新理念”的思想。
π类比正弦函数的性质得到:定义域、值域、最值、周期性(2)师生互动:
一起回顾正弦函数的性质,类比其性质,得到跟位置无关的性质;再结合余弦函数的图像,再得到跟位置有关的性质。并对比正弦、余弦函数的性质的异同。
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析设计意图:通过学生观察、类比、小组合作讨论得出余弦函数的性质,同时让学生自主发现,类比学习,达到了自主探究学习的目的。也充分体现师生互动的教学模式。
π学生再次讨论得到跟位置有关的性质:单调性、奇偶性、对称性、取得最值时x的集合
(三)余弦函数性质的应用
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析1、课本例题探讨
设计意图:
立足于课本,让学生熟练掌握函数图像常用的画法—五点法,并通过图像能够观察得到函数的性质。
2、课本思考交流:
设计意图:
有意识的训练学生借助图像进行分析解决问题的能力,强调图像的作用,渗透数形结合的数学思想方法,并且为下面求函数的定义域打好基础。 3、典型例题剖析: 例1:求下列函数的定义域 组A. (1)(2)组B.(1)(2)二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析 (2)通过两组题,着重强调了求函数定义域的关键是转化为解三角不等式,重点突出了图像在解题中的作用,让学生掌握数形结合的思想方法,从而达到了突破本节课的一个难点。
设计意图:
为了满足优生吃不饱的现象,我对求函数的定义域又作了一个课后展望:
求 函数的定义域,作为课后思考。
?
(1)为了掌握求函数的定义域的方法,我设计了例1,考虑到学生知识水平的差异性,我安排了A、B两组题,意在让学生根据自己的基础选用适合自己的题组,通过思考每位同学都能自主地完成,从而能让学生都能够体验到,获得知识时的一种成功感、喜悦感,而且又能够充分调动每位学生的学习的热情,体现了师生互动的课堂效果。
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(加强条件 ) 变式: 例2:求下列函数的值域: (1)二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析设计意图:
(1)到掌握求函数值域方法,我安排了例2,然后对条件进行加强和变式,让题目由浅入深,螺旋递进,使学生的知识逐渐深化。
(2)对于变式,再让学生小组合作讨论,后针对学生出现的各种情况,讨论a的符号对值域的影响,从而培养学生初步分类讨论的思想,有效激励学生探讨问题,掌握知识的方法,同时进一步体现教材的再度开发。
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(2)引申:设计意图:
①使学生把三角函数的内容跟二次函数的内容紧密的联系起来,能够把三角函数求值域转化为熟悉的二次函数求值域,设计了一道有关三角的二次函数求值域的题型。让学生体验知识之间的紧密联系。
②对于如何解这类型的题目时,我特别设置错误的结果,有意让学生从错误中深刻掌握,换元后的变量的有界性,我做了特别的强调。
③为了让学生进一步掌握这一类型的方法,我考虑对该题引申为带有参数,让学生作为课后探讨的内容,这也是再次用到分类讨论思想,进一步培养学生分析问题、讨论问题的完整性、周密性。
?
二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析(四)作业
(五)小结:
本节课由学生进行小结,提出掌握了哪些内容,还有哪些有疑惑。 二、学生分析三、教法分析四、过程分析五、评价分析一、教材分析五、评价分析 这是我对这一节课的大致设想,欢迎各位领导、老师多提宝贵意见。
?
谢谢!!
