第9章 9.2.1 向量的加法运算(二)(共57张PPT)
文档属性
| 名称 | 第9章 9.2.1 向量的加法运算(二)(共57张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-17 00:00:00 | ||
图片预览









文档简介
(共57张PPT)
第9章 9.2.1 向量的加减法
向量的加法运算
知识点一 向量加法的定义及其运算法则
1.向量加法的定义
求 的运算,叫作向量的加法.
任一向量与其相反向量的和是 .
两个向量和
零向量
向 量 求 和 的 法 则 三角形法则
这种求向量和的方法,称为向量加法的 法则.
三角形
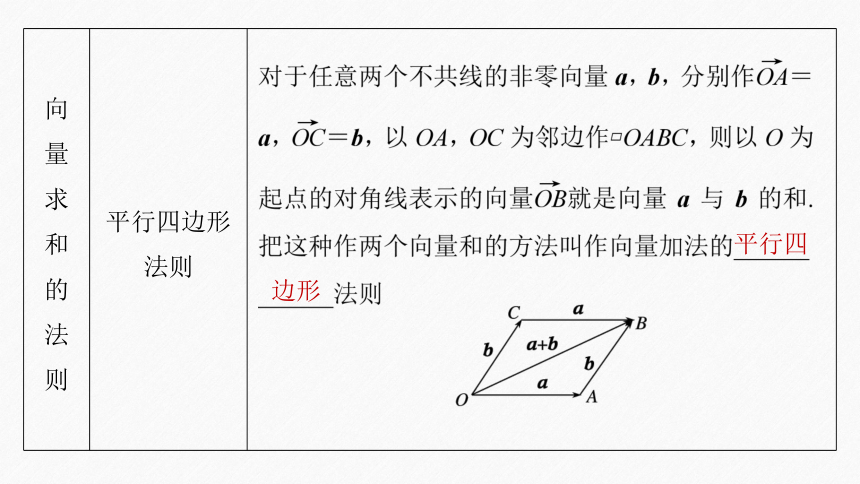
向 量 求 和 的 法 则 平行四边形法则
平行四
边形
的合成可以看作向量加法的三角形法则的物理模型, 的合成可以看作向量加法的平行四边形法则的物理模型.
思考 |a+b|与|a|,|b|有什么关系?
答案 (1)当向量a与b不共线时,a+b的方向与a,b不同,且|a+b|<|a|+|b|.
(2)当a与b同向时,a+b,a,b同向,且|a+b|=|a|+|b|.
(3)当a与b反向时,若|a|>|b|,则a+b的方向与a相同,且|a+b|=|a|-|b|;若|a|<|b|,则a+b的方向与b相同,且|a+b|=|b|-|a|.
位移
力
知识点二 向量加法的运算律
交换律 a+b=b+a
结合律 (a+b)+c=a+(b+c)
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
√
×
√
√
2
题型探究
PART TWO
一、向量加法法则
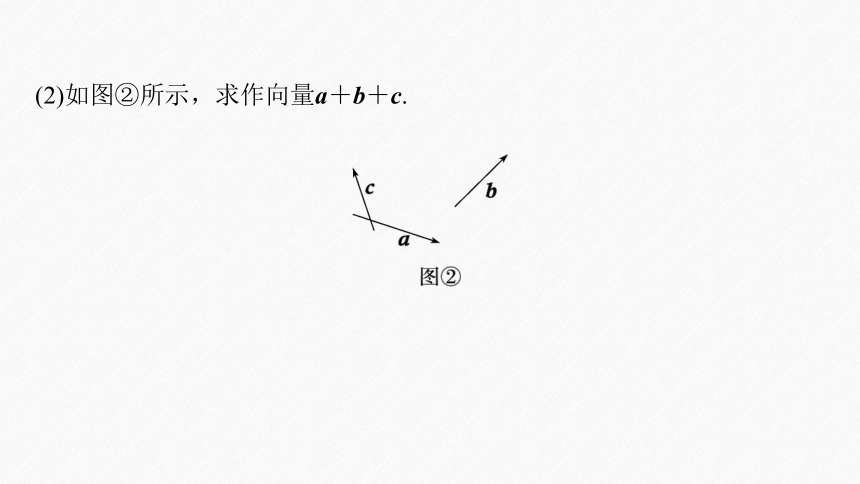
例1 (1)如图①所示,求作向量a+b;
(2)如图②所示,求作向量a+b+c.
解 方法一 (三角形法则)如图④所示,
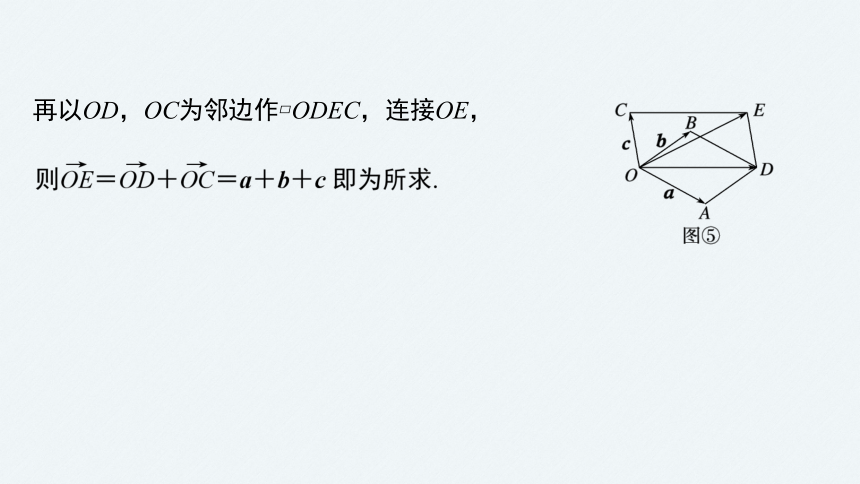
方法二 (平行四边形法则)如图⑤所示,
以OA,OB为邻边作 OADB,连接OD,
再以OD,OC为邻边作 ODEC,连接OE,
反思感悟
向量加法的三角形法则和平行四边形法则的区别和联系
区别 联系
三角形法则 (1)首尾相接 (2)适用于任何两个非零向量求和 当两个向量不共线时,三角形法则作出的图形是平行四边形法则作出图形的一半
平行四边形法则 (1)共起点 (2)仅适用于不共线的两个向量求和 跟踪训练1 如图所示,O为正六边形ABCDEF的中心,化简下列向量.
解析 因为四边形OABC是以OA,OC为邻边的平行四边形,OB是其对角线,
0
二、向量加法运算律的应用
反思感悟
向量加法运算律的意义和应用原则
(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现了恰当利用向量加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向量的加法运算可以按照任意的次序、任意的组合来进行.
(2)应用原则:通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.
三、向量加法的实际应用
解 设a,b分别表示水流的速度和小船在静水中的速度,
以OA,OB为邻边作矩形OACB,连接OC,
∴∠AOC=60°,
∴小船的实际航行速度为20 km/h,沿北偏东30°的方向航行.
反思感悟
应用向量解决实际问题的基本步骤
(1)表示:用向量表示有关量,将所要解答的问题转化为向量问题.
(2)运算:应用向量加法的平行四边形法则和三角形法则,将有关向量进行运算,解答向量问题.
(3)还原:根据向量的运算结果,结合向量共线、相等等概念解答原问题.
跟踪训练3 如图所示,已知电线AO与天花板的夹角为60°,电线AO所受拉力|F1|=24 N,绳BO与墙壁垂直,所受拉力|F2|=12 N,则F1和F2的
合力为______ N.
解析 如图,根据向量加法的平行四边形法则,
3
随堂演练
PART THREE
1
2
3
4
5
√
解析 根据平面向量的加法运算,得
1
2
3
4
5
√
1
2
3
4
5
√
1
2
3
4
5
√
1
2
3
4
5
5.若a表示“向东走8 km”,b表示“向北走8 km”,则|a+b|=______ km;向量a+b的方向为_______.
东北
因为∠AOB=45°,所以a+b的方向是东北.
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)向量加法的三角形法则和平行四边形法则.
(2)向量加法的运算律.
(3)向量加法的实际应用.
2.方法归纳:数形结合.
3.常见误区:向量加法的三角形法则要注意向量首尾相接,平行四边形法则要注意把向量移到共同起点.
4
课时对点练
PART FOUR
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故a+b的方向是北偏东30°.
又|a+b|=2 km,故选B.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
解析 由向量加法的平行四边形法则,知a+b=c成立,故|a+b|=|c|也成立;
由向量加法的三角形法则,知a+d=b成立,b+d=a不成立.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
e
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
以AB,AC为邻边作平行四边形ABDC,
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.在静水中船的速度为20 m/min,水流的速度为10 m/min,如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 作出图形,如图所示.
设船速v船与岸的方向成α角,
由图可知v水+v船=v实际,
结合已知条件,得四边形ABCD为平行四边形,
∴α=60°,从而船行进的方向与水流方向成120°角.
∴船沿与水流方向成120°角的方向行进.
11.(多选)下列说法错误的有
A.如果非零向量a与b的方向相同或相反,那么a+b的方向必与a或b的方
向相同
B.若向量a∥b,且|a|>|b|>0,则向量a+b的方向与向量a的方向相同
C.若 =0,则A,B,C一定为一个三角形的三个顶点
D.若a,b均为非零向量,则|a+b|=|a|+|b|
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
解析 A错,若a+b=0,则a+b的方向是任意的;
B正确,若a和b方向相同,则它们的和的方向应该与a(或b)的方向相同,若它们的方向相反,而a的模大于b的模,则它们的和的方向与a的方向相同;
C错,当A,B,C三点共线时,也满足 =0;
D错,|a+b|≤|a|+|b|.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.已知△ABC的三个顶点A,B,C及平面内一点P满足 ,
则下列结论中正确的是
A.P在△ABC的内部
B.P在△ABC的边AB上
C.P在AB边所在的直线上
D.P在△ABC的外部
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 ,根据向量加法的平行四边形法则,
如图,则点P在△ABC外.故选D.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(多选)已知平行四边形ABCD,设 =a,且b是一非零向量,则下列结论中正确的是
A.a∥b B.a+b=a
C.a+b=b D.|a+b|<|a|+|b|
√
√
所以a为零向量,
因为零向量和任意向量都平行,零向量和任意向量的和等于这个向量本身,
所以A,C正确,B,D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
①②③
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ①正确.以AB,AC为邻边作 ABDC,如图所示.
又∠A=90°,所以 ABDC为矩形,所以AD=BC,
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.设|a|=8,|b|=12,则|a+b|的最大值与最小值分别为______.
20,4
解析 当a,b共线同向时,|a+b|=|a|+|b|=8+12=20;
当a,b共线反向时,|a+b|=||a|-|b||=4;
当a,b不共线时,||a|-|b||<|a+b|<|a|+|b|,
即4<|a+b|<20.
所以最大值为20,最小值为4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
第9章 9.2.1 向量的加减法
向量的加法运算
知识点一 向量加法的定义及其运算法则
1.向量加法的定义
求 的运算,叫作向量的加法.
任一向量与其相反向量的和是 .
两个向量和
零向量
向 量 求 和 的 法 则 三角形法则
这种求向量和的方法,称为向量加法的 法则.
三角形
向 量 求 和 的 法 则 平行四边形法则
平行四
边形
的合成可以看作向量加法的三角形法则的物理模型, 的合成可以看作向量加法的平行四边形法则的物理模型.
思考 |a+b|与|a|,|b|有什么关系?
答案 (1)当向量a与b不共线时,a+b的方向与a,b不同,且|a+b|<|a|+|b|.
(2)当a与b同向时,a+b,a,b同向,且|a+b|=|a|+|b|.
(3)当a与b反向时,若|a|>|b|,则a+b的方向与a相同,且|a+b|=|a|-|b|;若|a|<|b|,则a+b的方向与b相同,且|a+b|=|b|-|a|.
位移
力
知识点二 向量加法的运算律
交换律 a+b=b+a
结合律 (a+b)+c=a+(b+c)
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
√
×
√
√
2
题型探究
PART TWO
一、向量加法法则
例1 (1)如图①所示,求作向量a+b;
(2)如图②所示,求作向量a+b+c.
解 方法一 (三角形法则)如图④所示,
方法二 (平行四边形法则)如图⑤所示,
以OA,OB为邻边作 OADB,连接OD,
再以OD,OC为邻边作 ODEC,连接OE,
反思感悟
向量加法的三角形法则和平行四边形法则的区别和联系
区别 联系
三角形法则 (1)首尾相接 (2)适用于任何两个非零向量求和 当两个向量不共线时,三角形法则作出的图形是平行四边形法则作出图形的一半
平行四边形法则 (1)共起点 (2)仅适用于不共线的两个向量求和 跟踪训练1 如图所示,O为正六边形ABCDEF的中心,化简下列向量.
解析 因为四边形OABC是以OA,OC为邻边的平行四边形,OB是其对角线,
0
二、向量加法运算律的应用
反思感悟
向量加法运算律的意义和应用原则
(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现了恰当利用向量加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向量的加法运算可以按照任意的次序、任意的组合来进行.
(2)应用原则:通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.
三、向量加法的实际应用
解 设a,b分别表示水流的速度和小船在静水中的速度,
以OA,OB为邻边作矩形OACB,连接OC,
∴∠AOC=60°,
∴小船的实际航行速度为20 km/h,沿北偏东30°的方向航行.
反思感悟
应用向量解决实际问题的基本步骤
(1)表示:用向量表示有关量,将所要解答的问题转化为向量问题.
(2)运算:应用向量加法的平行四边形法则和三角形法则,将有关向量进行运算,解答向量问题.
(3)还原:根据向量的运算结果,结合向量共线、相等等概念解答原问题.
跟踪训练3 如图所示,已知电线AO与天花板的夹角为60°,电线AO所受拉力|F1|=24 N,绳BO与墙壁垂直,所受拉力|F2|=12 N,则F1和F2的
合力为______ N.
解析 如图,根据向量加法的平行四边形法则,
3
随堂演练
PART THREE
1
2
3
4
5
√
解析 根据平面向量的加法运算,得
1
2
3
4
5
√
1
2
3
4
5
√
1
2
3
4
5
√
1
2
3
4
5
5.若a表示“向东走8 km”,b表示“向北走8 km”,则|a+b|=______ km;向量a+b的方向为_______.
东北
因为∠AOB=45°,所以a+b的方向是东北.
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)向量加法的三角形法则和平行四边形法则.
(2)向量加法的运算律.
(3)向量加法的实际应用.
2.方法归纳:数形结合.
3.常见误区:向量加法的三角形法则要注意向量首尾相接,平行四边形法则要注意把向量移到共同起点.
4
课时对点练
PART FOUR
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故a+b的方向是北偏东30°.
又|a+b|=2 km,故选B.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
解析 由向量加法的平行四边形法则,知a+b=c成立,故|a+b|=|c|也成立;
由向量加法的三角形法则,知a+d=b成立,b+d=a不成立.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
e
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
以AB,AC为邻边作平行四边形ABDC,
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.在静水中船的速度为20 m/min,水流的速度为10 m/min,如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 作出图形,如图所示.
设船速v船与岸的方向成α角,
由图可知v水+v船=v实际,
结合已知条件,得四边形ABCD为平行四边形,
∴α=60°,从而船行进的方向与水流方向成120°角.
∴船沿与水流方向成120°角的方向行进.
11.(多选)下列说法错误的有
A.如果非零向量a与b的方向相同或相反,那么a+b的方向必与a或b的方
向相同
B.若向量a∥b,且|a|>|b|>0,则向量a+b的方向与向量a的方向相同
C.若 =0,则A,B,C一定为一个三角形的三个顶点
D.若a,b均为非零向量,则|a+b|=|a|+|b|
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
解析 A错,若a+b=0,则a+b的方向是任意的;
B正确,若a和b方向相同,则它们的和的方向应该与a(或b)的方向相同,若它们的方向相反,而a的模大于b的模,则它们的和的方向与a的方向相同;
C错,当A,B,C三点共线时,也满足 =0;
D错,|a+b|≤|a|+|b|.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.已知△ABC的三个顶点A,B,C及平面内一点P满足 ,
则下列结论中正确的是
A.P在△ABC的内部
B.P在△ABC的边AB上
C.P在AB边所在的直线上
D.P在△ABC的外部
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 ,根据向量加法的平行四边形法则,
如图,则点P在△ABC外.故选D.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(多选)已知平行四边形ABCD,设 =a,且b是一非零向量,则下列结论中正确的是
A.a∥b B.a+b=a
C.a+b=b D.|a+b|<|a|+|b|
√
√
所以a为零向量,
因为零向量和任意向量都平行,零向量和任意向量的和等于这个向量本身,
所以A,C正确,B,D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
①②③
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ①正确.以AB,AC为邻边作 ABDC,如图所示.
又∠A=90°,所以 ABDC为矩形,所以AD=BC,
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.设|a|=8,|b|=12,则|a+b|的最大值与最小值分别为______.
20,4
解析 当a,b共线同向时,|a+b|=|a|+|b|=8+12=20;
当a,b共线反向时,|a+b|=||a|-|b||=4;
当a,b不共线时,||a|-|b||<|a+b|<|a|+|b|,
即4<|a+b|<20.
所以最大值为20,最小值为4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
