第9章 9.3.2 向量的坐标表示及向量线性运算的坐标表示(共59张PPT)
文档属性
| 名称 | 第9章 9.3.2 向量的坐标表示及向量线性运算的坐标表示(共59张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-17 21:23:39 | ||
图片预览







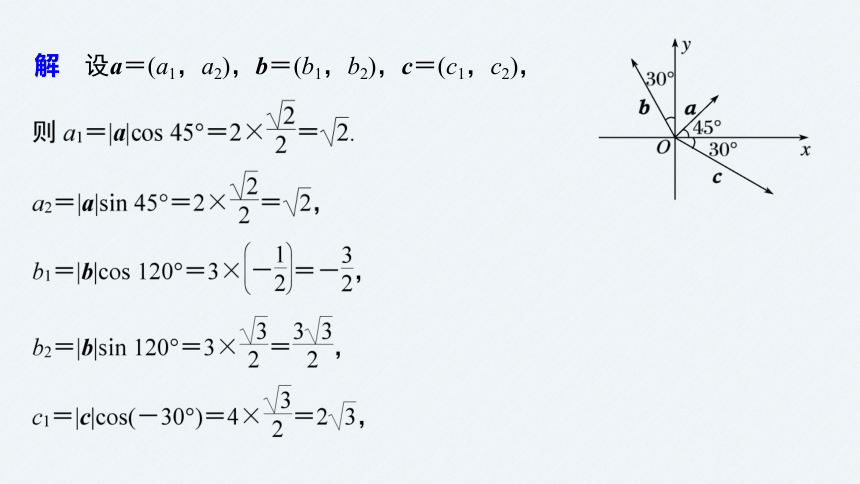
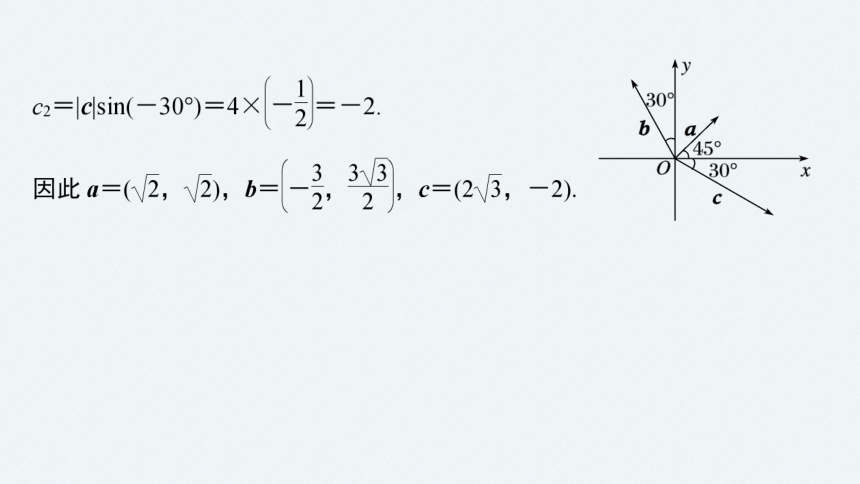


文档简介
(共59张PPT)
第9章 9.3.2 向量坐标表示与运算
向量的坐标表示及向量线性运算的坐标表示
知识点一 向量的坐标表示
1.向量的坐标
在平面直角坐标系中,分别取与x轴、y轴正方向相同的两个 i,j作为基底.对于平面内的向量a,由平面向量基本定理可知,有且只有一对有序实数(x,y),使得a=xi+yj,我们把有序实数对(x,y)称为向量a的(直角)坐标,记作a=(x,y).
单位向量
2.点的坐标与向量坐标的区别和联系
区别 表示形式不同 向量a=(x,y)中间用等号连接,而点A(x,y)中间没有等号
意义不同 点A(x,y)的坐标(x,y)表示点A在平面直角坐标系中的位置,a=(x,y)的坐标(x,y)既表示向量的大小,也表示向量的方向.另外(x,y)既可以表示点,也可以表示向量,叙述时应指明点(x,y)或向量(x,y)
联系 当平面向量的起点在原点时,平面向量的坐标与向量终点的坐标相同
知识点二 向量的坐标运算
1.设a=(x1,y1),b=(x2,y2)和实数λ
数学公式 文字语言表述
向量 加法 a+b=(x1+x2,y1+y2) 两个向量和的坐标分别等于这两个向量相应坐标的和
向量 减法 a-b=(x1-x2,y1-y2) 两个向量差的坐标分别等于这两个向量相应坐标的差
向量 数乘 λa=___________ 实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标
(λx1,λy1)
1.在平面直角坐标系内,若A(x1,y1),B(x2,y2),则向量 =(x1-x2,y1-y2).( )
2.与x轴,y轴正方向相同的两个单位向量分别为i=(1,0),j=(0,1).
( )
3.当向量的始点在坐标原点时,向量的坐标就是向量终点的坐标.
( )
4.相等向量的坐标与向量的起点、终点有关.( )
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
√
×
√
×
2
题型探究
PART TWO
一、向量的坐标表示
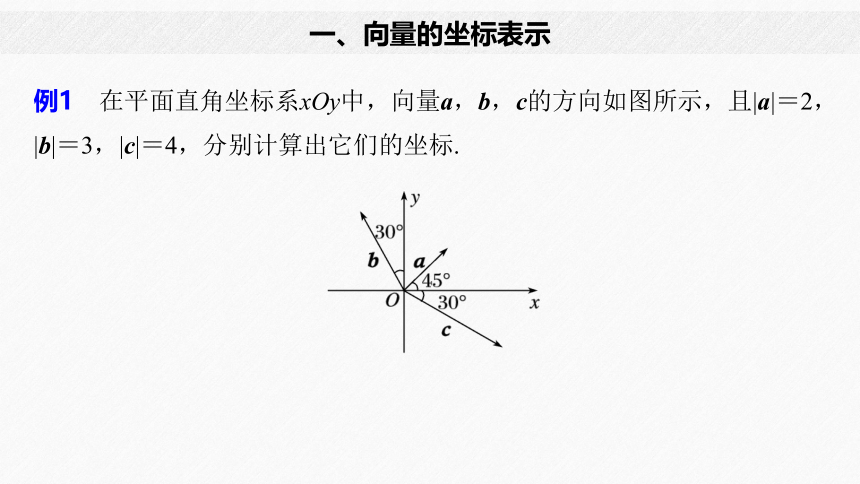
例1 在平面直角坐标系xOy中,向量a,b,c的方向如图所示,且|a|=2,|b|=3,|c|=4,分别计算出它们的坐标.
解 设a=(a1,a2),b=(b1,b2),c=(c1,c2),
反思感悟
在表示点、向量的坐标时,可利用向量的相等、加减法运算等求坐标,也可以利用向量、点的坐标定义求坐标.
跟踪训练1 已知O是坐标原点,点A在第二象限, =6,∠xOA=150°,向量 的坐标为__________.
解析 设点A(x,y),
二、向量的坐标运算
例2 已知a=(-1,2),b=(2,1),求:
(1)2a+3b;
解 2a+3b=2(-1,2)+3(2,1)
=(-2,4)+(6,3)=(4,7).
(2)a-3b;
解 a-3b=(-1,2)-3(2,1)
=(-1,2)-(6,3)=(-7,-1).
反思感悟
向量坐标运算的方法
(1)若已知向量的坐标,则直接应用两个向量和、差及向量数乘的运算法则进行.
(2)若已知有向线段两端点的坐标,则可先求出向量的坐标,然后再进行向量的坐标运算.
(3)向量的线性坐标运算可完全类比数的运算进行.
√
三、向量坐标运算的应用
解析 设点P的坐标为(x,y),∵点P在线段P1P2上,
反思感悟
坐标形式下向量相等的条件:相等向量的对应坐标相等;对应坐标相等的向量是相等向量.由此可建立相等关系求某些参数的值.
(0,2)
核心素养之逻辑推理
HE XIN SU YANG ZHI LUO JI TUI LI
解 设P(x,y).
∴(x-x1,y-y1)=λ(x2-x,y2-y),
(2)如图,△ABC的三个顶点的坐标分别为A(x1,y1),B(x2,y2),C(x3,y3),D是边AB的中点,G是CD上的一点,且 =2,求点G的坐标.
解 ∵D是AB的中点,
设G点坐标为(x,y),由定比分点坐标公式可得
素养
提升
(1)用有向线段的定比分点坐标公式 可以求解有向
线段的定比分点坐标及定点分有向线段所成的比.事实上用这个公式,还可巧妙地用于解决其他一些问题.如用得好,会使解题过程显得别具一格,简捷明快,充分展现我们思维的独创性.定比分点坐标公式也是判定或证明两向量是否共线、平行的有效方法.
(2)通过定比分点坐标公式的推导与应用,培养逻辑推理和数学运算素养.
3
随堂演练
PART THREE
1
2
3
4
5
√
1
2
3
4
5
2.已知 =(-2,4),则下列说法正确的是
A.点A的坐标是(-2,4)
B.点B的坐标是(-2,4)
C.当点B是坐标原点时,点A的坐标是(-2,4)
D.当点A是坐标原点时,点B的坐标是(-2,4)
√
解析 由任一向量的坐标的定义可知,当A是坐标原点时,点B的坐标是(-2,4).
1
2
3
4
5
√
1
2
3
4
5
(-2,-4)
1
2
3
4
5
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)向量的坐标表示.
(2)向量加、减、数乘运算的坐标表示.
2.方法归纳:数形结合.
3.常见误区:混淆点的坐标与向量的坐标致错.
4
课时对点练
PART FOUR
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.已知点A(1,1),B(2,4),将向量 向右平移1个单位长度,再向下平移1个单位长度,所得向量 的坐标是
A.(2,0) B.(3,3) C.(1,3) D.(3,4)
√
解析 ∵点A(1,1),B(2,4),
再向下平移1个单位长度后,向量的大小和方向没有变化,
2.(多选)下面几种说法中正确的有
A.相等向量的坐标相同
B.平面上一个向量对应于平面上唯一的坐标
C.一个坐标对应于唯一的一个向量
D.平面上一个点与以原点为始点、该点为终点的向量一一对应
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
解析 由向量坐标的定义不难看出一个坐标可对应无数个相等的向量,故C错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.(1,-2) B.(7,6) C.(5,0) D.(11,8)
√
解析 设c=xa+yb,
∴c=3a-b.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.若向量a=(1,1),b=(-1,1),c=(4,2),则c等于
A.3a-b B.3a+b C.-a+3b D.a+3b
√
所以(x-5,y+1)=(2,-5),
所以x=7,y=-6.即D(7,-6).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.已知四边形ABCD为平行四边形,其中A(5,-1),B(-1,7),C(1,2),则顶点D的坐标为
A.(-7,0) B.(7,6) C.(6,7) D.(7,-6)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.已知a+b=(1,3),a-b=(5,7),则a=_______,b=___________.
(3,5) (-2,-2)
解析 由a+b=(1,3),a-b=(5,7),
所以2a=(1,3)+(5,7)=(6,10),
所以a=(3,5),2b=(1,3)-(5,7)=(-4,-4),
所以b=(-2,-2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(7,7)
设O为坐标原点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知A(1,0),B(3,4),M是线段AB的中点,那么向量 的坐标是________.
(1,2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设点C(x1,y1),D(x2,y2),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴C,D的坐标分别为(0,4)和(-2,0),
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.若α,β是一组基底,向量γ=xα+yβ(x,y∈R),则称(x,y)为向量γ在基底α,β下的坐标.现已知向量a在基底p=(1,-1),q=(2,1)下的坐标为(-2,2),则a在另一组基底m=(-1,1),n=(1,2)下的坐标为
A.(2,0) B.(0,-2) C.(-2,0) D.(0,2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 ∵a在基底p,q下的坐标为(-2,2),
∴a=-2p+2q=-2(1,-1)+2(2,1)=(2,4).
令a=xm+yn=(-x+y,x+2y),
∴a在基底m,n下的坐标为(0,2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
14.如图,在6×6的方格纸中,若起点和终点均在格点的向量a,b,c满足c=xa+yb(x,y∈R),则x+y=________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 建立如图所示的平面直角坐标系,设小方格的边长为1,
则可得a=(1,2),b=(2,-3),c=(3,4).
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.已知集合M={a|a=(1,2)+λ(3,4),λ∈R},N={a|a=(-2,-2)+μ(4,5),μ∈R},则M∩N等于
A.{(1,1)} B.{(1,2),(-2,-2)}
C.{(-2,-2)} D.
√
解析 设a∈M∩N,则存在λ和μ使得(1,2)+λ(3,4)=(-2,-2)+μ(4,5),
即(3,4)=(4μ-3λ,5μ-4λ).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故四边形OABP不能成为平行四边形.
(2)四边形OABP能为平行四边形吗?若能,求t值;若不能,说明理由.
本课结束
第9章 9.3.2 向量坐标表示与运算
向量的坐标表示及向量线性运算的坐标表示
知识点一 向量的坐标表示
1.向量的坐标
在平面直角坐标系中,分别取与x轴、y轴正方向相同的两个 i,j作为基底.对于平面内的向量a,由平面向量基本定理可知,有且只有一对有序实数(x,y),使得a=xi+yj,我们把有序实数对(x,y)称为向量a的(直角)坐标,记作a=(x,y).
单位向量
2.点的坐标与向量坐标的区别和联系
区别 表示形式不同 向量a=(x,y)中间用等号连接,而点A(x,y)中间没有等号
意义不同 点A(x,y)的坐标(x,y)表示点A在平面直角坐标系中的位置,a=(x,y)的坐标(x,y)既表示向量的大小,也表示向量的方向.另外(x,y)既可以表示点,也可以表示向量,叙述时应指明点(x,y)或向量(x,y)
联系 当平面向量的起点在原点时,平面向量的坐标与向量终点的坐标相同
知识点二 向量的坐标运算
1.设a=(x1,y1),b=(x2,y2)和实数λ
数学公式 文字语言表述
向量 加法 a+b=(x1+x2,y1+y2) 两个向量和的坐标分别等于这两个向量相应坐标的和
向量 减法 a-b=(x1-x2,y1-y2) 两个向量差的坐标分别等于这两个向量相应坐标的差
向量 数乘 λa=___________ 实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标
(λx1,λy1)
1.在平面直角坐标系内,若A(x1,y1),B(x2,y2),则向量 =(x1-x2,y1-y2).( )
2.与x轴,y轴正方向相同的两个单位向量分别为i=(1,0),j=(0,1).
( )
3.当向量的始点在坐标原点时,向量的坐标就是向量终点的坐标.
( )
4.相等向量的坐标与向量的起点、终点有关.( )
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
√
×
√
×
2
题型探究
PART TWO
一、向量的坐标表示
例1 在平面直角坐标系xOy中,向量a,b,c的方向如图所示,且|a|=2,|b|=3,|c|=4,分别计算出它们的坐标.
解 设a=(a1,a2),b=(b1,b2),c=(c1,c2),
反思感悟
在表示点、向量的坐标时,可利用向量的相等、加减法运算等求坐标,也可以利用向量、点的坐标定义求坐标.
跟踪训练1 已知O是坐标原点,点A在第二象限, =6,∠xOA=150°,向量 的坐标为__________.
解析 设点A(x,y),
二、向量的坐标运算
例2 已知a=(-1,2),b=(2,1),求:
(1)2a+3b;
解 2a+3b=2(-1,2)+3(2,1)
=(-2,4)+(6,3)=(4,7).
(2)a-3b;
解 a-3b=(-1,2)-3(2,1)
=(-1,2)-(6,3)=(-7,-1).
反思感悟
向量坐标运算的方法
(1)若已知向量的坐标,则直接应用两个向量和、差及向量数乘的运算法则进行.
(2)若已知有向线段两端点的坐标,则可先求出向量的坐标,然后再进行向量的坐标运算.
(3)向量的线性坐标运算可完全类比数的运算进行.
√
三、向量坐标运算的应用
解析 设点P的坐标为(x,y),∵点P在线段P1P2上,
反思感悟
坐标形式下向量相等的条件:相等向量的对应坐标相等;对应坐标相等的向量是相等向量.由此可建立相等关系求某些参数的值.
(0,2)
核心素养之逻辑推理
HE XIN SU YANG ZHI LUO JI TUI LI
解 设P(x,y).
∴(x-x1,y-y1)=λ(x2-x,y2-y),
(2)如图,△ABC的三个顶点的坐标分别为A(x1,y1),B(x2,y2),C(x3,y3),D是边AB的中点,G是CD上的一点,且 =2,求点G的坐标.
解 ∵D是AB的中点,
设G点坐标为(x,y),由定比分点坐标公式可得
素养
提升
(1)用有向线段的定比分点坐标公式 可以求解有向
线段的定比分点坐标及定点分有向线段所成的比.事实上用这个公式,还可巧妙地用于解决其他一些问题.如用得好,会使解题过程显得别具一格,简捷明快,充分展现我们思维的独创性.定比分点坐标公式也是判定或证明两向量是否共线、平行的有效方法.
(2)通过定比分点坐标公式的推导与应用,培养逻辑推理和数学运算素养.
3
随堂演练
PART THREE
1
2
3
4
5
√
1
2
3
4
5
2.已知 =(-2,4),则下列说法正确的是
A.点A的坐标是(-2,4)
B.点B的坐标是(-2,4)
C.当点B是坐标原点时,点A的坐标是(-2,4)
D.当点A是坐标原点时,点B的坐标是(-2,4)
√
解析 由任一向量的坐标的定义可知,当A是坐标原点时,点B的坐标是(-2,4).
1
2
3
4
5
√
1
2
3
4
5
(-2,-4)
1
2
3
4
5
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)向量的坐标表示.
(2)向量加、减、数乘运算的坐标表示.
2.方法归纳:数形结合.
3.常见误区:混淆点的坐标与向量的坐标致错.
4
课时对点练
PART FOUR
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.已知点A(1,1),B(2,4),将向量 向右平移1个单位长度,再向下平移1个单位长度,所得向量 的坐标是
A.(2,0) B.(3,3) C.(1,3) D.(3,4)
√
解析 ∵点A(1,1),B(2,4),
再向下平移1个单位长度后,向量的大小和方向没有变化,
2.(多选)下面几种说法中正确的有
A.相等向量的坐标相同
B.平面上一个向量对应于平面上唯一的坐标
C.一个坐标对应于唯一的一个向量
D.平面上一个点与以原点为始点、该点为终点的向量一一对应
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
解析 由向量坐标的定义不难看出一个坐标可对应无数个相等的向量,故C错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.(1,-2) B.(7,6) C.(5,0) D.(11,8)
√
解析 设c=xa+yb,
∴c=3a-b.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.若向量a=(1,1),b=(-1,1),c=(4,2),则c等于
A.3a-b B.3a+b C.-a+3b D.a+3b
√
所以(x-5,y+1)=(2,-5),
所以x=7,y=-6.即D(7,-6).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.已知四边形ABCD为平行四边形,其中A(5,-1),B(-1,7),C(1,2),则顶点D的坐标为
A.(-7,0) B.(7,6) C.(6,7) D.(7,-6)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.已知a+b=(1,3),a-b=(5,7),则a=_______,b=___________.
(3,5) (-2,-2)
解析 由a+b=(1,3),a-b=(5,7),
所以2a=(1,3)+(5,7)=(6,10),
所以a=(3,5),2b=(1,3)-(5,7)=(-4,-4),
所以b=(-2,-2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(7,7)
设O为坐标原点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知A(1,0),B(3,4),M是线段AB的中点,那么向量 的坐标是________.
(1,2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设点C(x1,y1),D(x2,y2),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴C,D的坐标分别为(0,4)和(-2,0),
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.若α,β是一组基底,向量γ=xα+yβ(x,y∈R),则称(x,y)为向量γ在基底α,β下的坐标.现已知向量a在基底p=(1,-1),q=(2,1)下的坐标为(-2,2),则a在另一组基底m=(-1,1),n=(1,2)下的坐标为
A.(2,0) B.(0,-2) C.(-2,0) D.(0,2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 ∵a在基底p,q下的坐标为(-2,2),
∴a=-2p+2q=-2(1,-1)+2(2,1)=(2,4).
令a=xm+yn=(-x+y,x+2y),
∴a在基底m,n下的坐标为(0,2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
14.如图,在6×6的方格纸中,若起点和终点均在格点的向量a,b,c满足c=xa+yb(x,y∈R),则x+y=________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 建立如图所示的平面直角坐标系,设小方格的边长为1,
则可得a=(1,2),b=(2,-3),c=(3,4).
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.已知集合M={a|a=(1,2)+λ(3,4),λ∈R},N={a|a=(-2,-2)+μ(4,5),μ∈R},则M∩N等于
A.{(1,1)} B.{(1,2),(-2,-2)}
C.{(-2,-2)} D.
√
解析 设a∈M∩N,则存在λ和μ使得(1,2)+λ(3,4)=(-2,-2)+μ(4,5),
即(3,4)=(4μ-3λ,5μ-4λ).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故四边形OABP不能成为平行四边形.
(2)四边形OABP能为平行四边形吗?若能,求t值;若不能,说明理由.
本课结束
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
