鲁教版(五四制)数学七年级下册 第十一章 一元一次不等式与一元一次不等式组 复习 课件(共29张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级下册 第十一章 一元一次不等式与一元一次不等式组 复习 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 615.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-17 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
第十一章 一元一次不等式与一元一次不等式组
复习课件
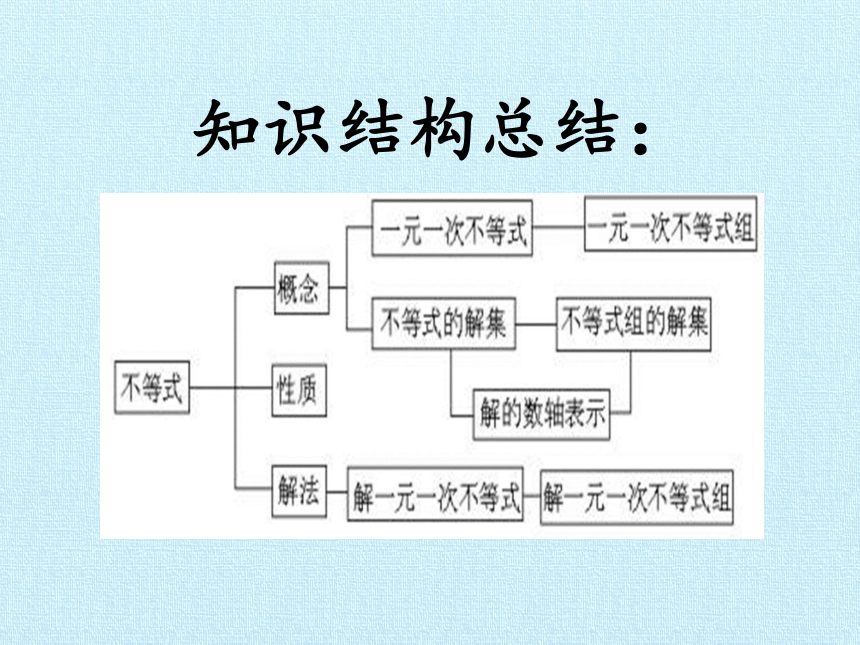
知识结构总结:
思想方法总结:
数形结合的思想
类比法
主要知识点:
1.不等关系
2.不等式的基本性质
3.解一元一次不等式
4.解一元一次不等式组
1.不等关系
用符号“>、≥、<、≤、≠”连接的
式子叫做不等式。
如:用不等式表示
(1)a是非负数;
(2)a与b的平方和不大于3;
(3)x除以2的商与4的和,至多为5;
(4)用长度为a的绳子,围成一个圆,若使圆的面积不小于100,那么绳长a应满足怎样的关系式?
2.不等式的基本性质
性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
性质2:不等式的两边都乘以(或除以)
同一个正数,不等号的方向不变;
性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
如:已知a<b,用“<”或“>”填空
(1)a-3_____b-3;
(2)6a_____6b;
(3)-a_____-b;
(4)a-b_____0;2a_____a+b
(5)若a<b<0,则a2_____a, ____1
2.不等式的基本性质
<
<
<
>
>
>
<
讨论:2a一定比a大吗?
>
>
>
<
如果 ,那么:
①
②
③
④
(不等式性质 )
(不等式性质 )
(不等式性质 )
(不等式性质 )
1
2
3
1
实数a,b,c在数轴上的对应点,如图所示,则下列各式中正确的是( )
A.bc>ab B.ac<ab
C.cb<ab D.c+b>a+b
b
c
0
a
A
例6:若 则( )
D
一般步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化。
(不要漏乘不含分母的项)
(要变号)
(注意何时改变不等号方向)
把解集表示在数轴上时,需注意:
(1)空心、实心小圆圈的区别;
(2)“>、≥”向右拐,“<、≤”向左拐。
3.解一元一次不等式
不等式的解集在数轴上的表示:大向右,小向左,有等号是实心,无等号是空心。
求几个不等式的解的公共部分的方法和规律:
(1)数轴法
(2)口诀法:
同大取大
同小取小
大小小大中间找
大大小小解不了
解下列不等式:
一般步骤:
(1)分别解出各不等式;
(2)在数轴上表示各不等式的解集;
(3)找出各解集的公共部分;
(4)下结论;
4.解一元一次不等式组
同大取大,同小取小
大小小大中间找,
大大小小解不了。
解下列不等式组:
1、用>、<填空。(若a>b,c不为0。)
c-a c-b
2a a+b
-
m
4y
m
3x
4y
(4)3x
>
-
>
2
5a
a
5
(3)a
-
-
>
mb
ma
b
(2)a
>
<
m
n
x
n
(1)mx
<
<
指出下列各式成立的条件:
2、
3、根据基本性质,把下列不等式化成x>a或x4、设a>b,用“>”或“<”号填空:
(5)若(K-1)X1,则K满足:
A.K<-1 B.K>-1 C.K<1 D.K>1
7、求不等式10(x+4)+x≤84的非负整数解。
8、求不等式的非负整数解
6、解不等式ax+b>0和ax+b<0
10、m为何值时,关于x的方程
3(2x-3m)-2(x+4m)=4(5-x)的解是非正数?
13、已知关于x,y的方程组
的解为正数,
(1)求:m的范围?(2)化简
16、已知-317、若关于x的方程5x-(4k-1)=7x+4k-3
的解是:(1)非负数(2)负数;
试确定k的取值范围。
18、若关于x的不等式组
的解集为 ,求a的范围?
19、若不等式组 的解集是 ,
求不等式 的解集。
21、三个连续正整数的和不大于17,求这三个数。
24、若不等式组 无解,求m的范围?
23、若不等式组 无解,求a的取值范围。
26、设x>y,试比较代数式–(8–10x)和–(8–10y)的大小。如果较大的代数式为正数,则其中最小的正整数x或y的值是多少?
27、若-m,1-m,m,m+1四个数在数轴上所对应的点是从左到右排列,则m的范围是?
谢 谢
第十一章 一元一次不等式与一元一次不等式组
复习课件
知识结构总结:
思想方法总结:
数形结合的思想
类比法
主要知识点:
1.不等关系
2.不等式的基本性质
3.解一元一次不等式
4.解一元一次不等式组
1.不等关系
用符号“>、≥、<、≤、≠”连接的
式子叫做不等式。
如:用不等式表示
(1)a是非负数;
(2)a与b的平方和不大于3;
(3)x除以2的商与4的和,至多为5;
(4)用长度为a的绳子,围成一个圆,若使圆的面积不小于100,那么绳长a应满足怎样的关系式?
2.不等式的基本性质
性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
性质2:不等式的两边都乘以(或除以)
同一个正数,不等号的方向不变;
性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
如:已知a<b,用“<”或“>”填空
(1)a-3_____b-3;
(2)6a_____6b;
(3)-a_____-b;
(4)a-b_____0;2a_____a+b
(5)若a<b<0,则a2_____a, ____1
2.不等式的基本性质
<
<
<
>
>
>
<
讨论:2a一定比a大吗?
>
>
>
<
如果 ,那么:
①
②
③
④
(不等式性质 )
(不等式性质 )
(不等式性质 )
(不等式性质 )
1
2
3
1
实数a,b,c在数轴上的对应点,如图所示,则下列各式中正确的是( )
A.bc>ab B.ac<ab
C.cb<ab D.c+b>a+b
b
c
0
a
A
例6:若 则( )
D
一般步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化。
(不要漏乘不含分母的项)
(要变号)
(注意何时改变不等号方向)
把解集表示在数轴上时,需注意:
(1)空心、实心小圆圈的区别;
(2)“>、≥”向右拐,“<、≤”向左拐。
3.解一元一次不等式
不等式的解集在数轴上的表示:大向右,小向左,有等号是实心,无等号是空心。
求几个不等式的解的公共部分的方法和规律:
(1)数轴法
(2)口诀法:
同大取大
同小取小
大小小大中间找
大大小小解不了
解下列不等式:
一般步骤:
(1)分别解出各不等式;
(2)在数轴上表示各不等式的解集;
(3)找出各解集的公共部分;
(4)下结论;
4.解一元一次不等式组
同大取大,同小取小
大小小大中间找,
大大小小解不了。
解下列不等式组:
1、用>、<填空。(若a>b,c不为0。)
c-a c-b
2a a+b
-
m
4y
m
3x
4y
(4)3x
>
-
>
2
5a
a
5
(3)a
-
-
>
mb
ma
b
(2)a
>
<
m
n
x
n
(1)mx
<
<
指出下列各式成立的条件:
2、
3、根据基本性质,把下列不等式化成x>a或x
(5)若(K-1)X
A.K<-1 B.K>-1 C.K<1 D.K>1
7、求不等式10(x+4)+x≤84的非负整数解。
8、求不等式的非负整数解
6、解不等式ax+b>0和ax+b<0
10、m为何值时,关于x的方程
3(2x-3m)-2(x+4m)=4(5-x)的解是非正数?
13、已知关于x,y的方程组
的解为正数,
(1)求:m的范围?(2)化简
16、已知-3
的解是:(1)非负数(2)负数;
试确定k的取值范围。
18、若关于x的不等式组
的解集为 ,求a的范围?
19、若不等式组 的解集是 ,
求不等式 的解集。
21、三个连续正整数的和不大于17,求这三个数。
24、若不等式组 无解,求m的范围?
23、若不等式组 无解,求a的取值范围。
26、设x>y,试比较代数式–(8–10x)和–(8–10y)的大小。如果较大的代数式为正数,则其中最小的正整数x或y的值是多少?
27、若-m,1-m,m,m+1四个数在数轴上所对应的点是从左到右排列,则m的范围是?
谢 谢
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
