2.4 自由落体运动教案-2022-2023学年高一上学期物理人教版(2019)必修第一册
文档属性
| 名称 | 2.4 自由落体运动教案-2022-2023学年高一上学期物理人教版(2019)必修第一册 |  | |
| 格式 | zip | ||
| 文件大小 | 258.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-17 18:45:42 | ||
图片预览




文档简介
自由落体运动
知识点总结
考点一、自由落体运动
1、定义:物体只在重力作用下从静止开始的运动叫自由落体运动。
2、条件:只受重力作用;初速度为0
3、运动性质
自由落体运动是初速度为零,加速度的匀加速直线运动,它是我们前面所学的匀变速直线运动的一个特例,其v-t图像是一条过原点的倾斜直线,斜率
4、对自由落体运动的理解
(1)自由落体是一种理想化模型,这种模型忽略了次要因素----空气阻力,突出了主要因素----重力。实际上,物体下落时由于受空气阻力的作用,并不做自由落体运动。但是,当空气阻力远小于物体的重力时,可以认为物体只受重力作用,此时物体由静止下落就可以看作自由落体运动。比如,在空气中石块的下落,在短时间内可以看作自由落体运动,而在空气中羽毛的下落不能看作自由落体运动。
(2)自由落体运动在其他星球上也可以发生,但物体下落时的加速度和在地球上的一般不同。
考点二、自由落体运动的实验探究
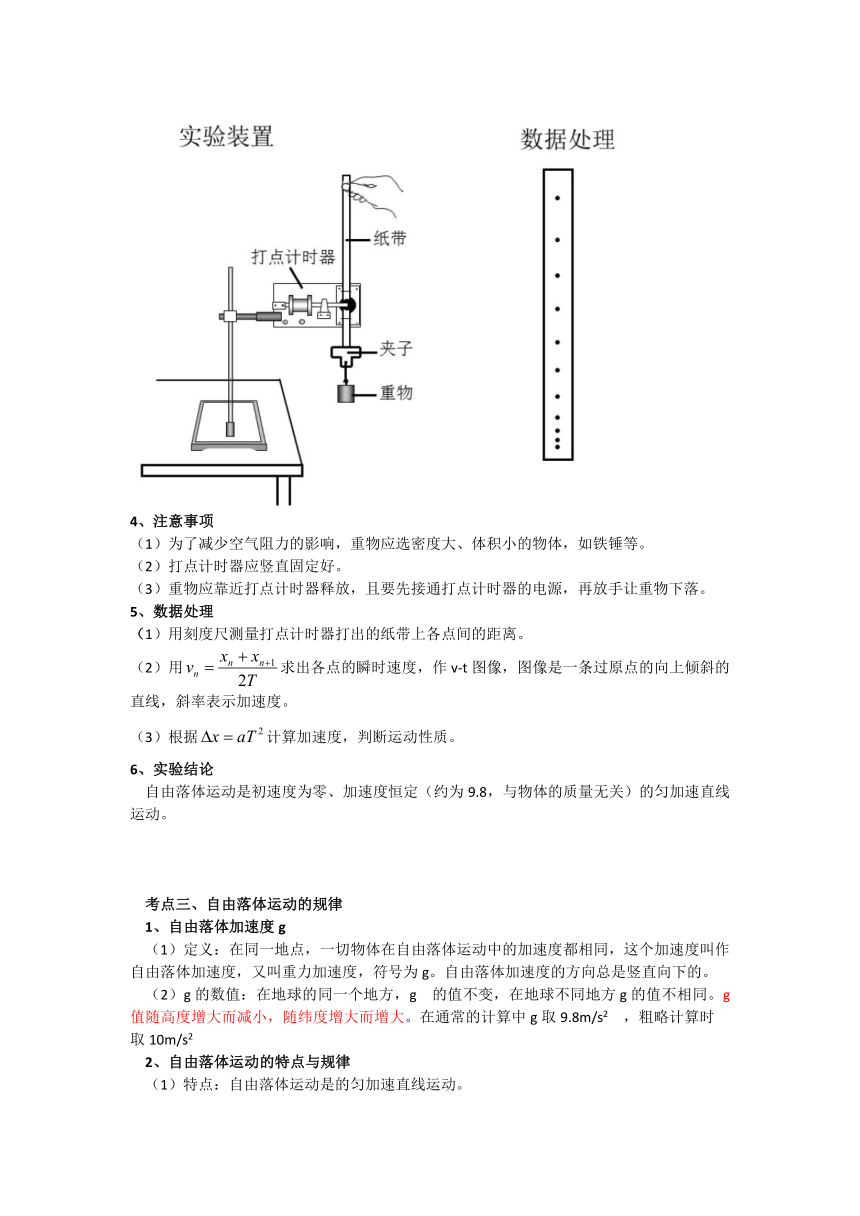
1、实验原理
重物拖着纸带竖直下落时,如果纸带阻力和空气阻力比重物的重力小得多,可以近似认为重物仅在重力作用下运动,根据打点计时器打出的纸带能分析和研究重物的运动规律。
2、实验器材
打点计时器(带导线)、纸带、复写纸、带铁夹的铁架台、几个质量不同的重物、夹子、低压交流电、毫米刻度尺
3、探究过程
(1)如图所示,将打点计时器竖直固定在铁架台上,连接好电路。
(2)把纸带穿过两个限位孔,下端用铁夹夹到重物上,让重物靠近打点计时器。
(3)用手捏住纸带上端把纸带拉成竖直状态,接通电源,松开纸带让重物自由下落,重物落地后立即关闭电源,打点计时器就在纸带上打下一系列的点。
(4)改变重物的质量,重复几次上面的实验,选取一条点迹清晰的纸带进行分析。
4、注意事项
(1)为了减少空气阻力的影响,重物应选密度大、体积小的物体,如铁锤等。
(2)打点计时器应竖直固定好。
(3)重物应靠近打点计时器释放,且要先接通打点计时器的电源,再放手让重物下落。
5、数据处理
(1)用刻度尺测量打点计时器打出的纸带上各点间的距离。
(2)用求出各点的瞬时速度,作v-t图像,图像是一条过原点的向上倾斜的直线,斜率表示加速度。
(3)根据计算加速度,判断运动性质。
6、实验结论
自由落体运动是初速度为零、加速度恒定(约为9.8,与物体的质量无关)的匀加速直线运动。
考点三、自由落体运动的规律
1、自由落体加速度g
(1)定义:在同一地点,一切物体在自由落体运动中的加速度都相同,这个加速度叫作自由落体加速度,又叫重力加速度,符号为g。自由落体加速度的方向总是竖直向下的。
(2)g的数值:在地球的同一个地方,g 的值不变,在地球不同地方g的值不相同。g值随高度增大而减小,随纬度增大而增大。在通常的计算中g取9.8m/s2 ,粗略计算时 取10m/s2
2、自由落体运动的特点与规律
(1)特点:自由落体运动是的匀加速直线运动。
(2)规律:
①速度公式位移公式:
②位移公式:
③速度与位移的关系式 (为物体下落的高度,不是距离地面的高度)。
3、自由落体运动的推论
(1)连续相等时间t内高度差:
(2)物体的平均速度:=
(3)第1个T内,第2个T内,第3个T内,···,第 个T内下落的高度之比:
下落连续相同的高度所用间之比:
考点四:计算重力加速度常见方法
方法一:利用相邻的、相等的时间间隔的位移差相等,且为一定值,即,则
方法二:可由位移公式求得。利用刻度尺量出从初始位置到某点的位移,若已知发生这段位移的时间,则。可以找多个点,多次求g值,再求平均值。
方法三:可利用速度公式求得。利用平均速度求某一点的瞬时速度,并已知自由下落的物体经过这一点的时间,则由解得,当然亦可多找点,多次求瞬时速度,多次求g值,再求平均值。
方法四:利用多次求得的瞬时速度,画出v-t图像,根据图像的斜率求得g。
方法五:用滴水法可以测定重力加速度的值。
方法是:在自来水龙头下面固定一块挡板A,使水一滴一滴连续地滴落到挡板上,如图所示,仔细调节水龙头,使得耳朵刚好听到前一个水滴滴在挡板上的声音的同时,下一个水滴刚好开始下落。首先量出水龙头口离挡板的高度h,再用停表计时。计时方法是:当听到某一水滴滴在挡板上的声音的同时,开启停表开始计时,并数“1”,以后每听到一声水滴声,依次
数“2,3,·..”,一直数到“n”,按下停表按钮停止时,读出停表的示数为
t。根据以上数据可求。
由上可知,相邻两滴水声的间隔就是水滴自由下落的时间,故,由得
题型总结:
1、(多选)一名宇航员在某星球上完成自由落体运动实验,让一个质量为 2kg 的小球从一定的高度自由下落,测得在第 5s 内的位移是 18m ,则( )
A.物体在 2s 末的速度是 8m/s
B.物体在第 5s 内的平均速度是 3.6m/s
C.物体自由下落的加速度是
D.物体在 5s 内的位移是 50m
2、(多选)跳水运动员训练时从十米跳台双脚朝下自由落下,某同学利用手机的连拍功能,连拍了多张照片。测得其中三张连续的照片中运动员双脚离水面的高度分别为 、 和 ,自由落体加速度 g 取 ,则( )
A.运动员双脚入水时的速度为
B.拍第二张照片时运动员的瞬时速度为
C.第三张照片中运动员双脚离水面的高度
D.手机连拍的时间间隔是 0.2s
3、一个物体做自由落体运动, 3s 末物体落地。若物体在第 1s 内下落的位移为 ,则( )
A.物体下落的加速度为
B.物体在 2s 末的速度为 20m/s
C.物体在第 2s 内下落的位移为
D.物体下落的总位移为
4、一个自由落体的物体,到达地面时的速度为 30m/s ,取 g =10m/s 2 ,则下落的高度为( )
A.40m B.45m C.60m D.65m
5、(多选)如图所示,甲同学拿着一把长 50cm 的直尺,乙同学把手放在 0 刻度线处准备抓尺,测反应时间。第一次乙同学抓住直尺位置的刻度值为 20cm ;重复实验,第二次手抓住直尺位置的刻度值为 10cm ,取 。下列说法正确的是( )
A.乙同学第一次的 “ 反应时间 ” 比第二次长
B.乙同学第一次抓住直尺之前的瞬间,直尺的速度约为
C.若某同学的“反应时间”大于,则用该直尺将无法用上述方法测量他的“反应时间”
D.若将尺子上原来的长度值改为对应的 “ 反应时间 ” 值,则可用上述方法直接测出“反应时间”
6、
15.
如图所示,在一个桌面上方有三个金属小球 a 、 b 、 c ,离桌面高度分别为 。若先后顺次释放 a 、 b 、 c ,三球刚好同时落到桌面上,不计空气阻力,则( )
A. b 与 a 开始下落的时间差小于 c 与 b 开始下落的时间差
B.三者到达桌面时的速度之比是 3∶2∶1
C.三者运动时间之比为 3∶2∶1
D.三个小球运动的加速度与小球受到的重力成正比,与质量成反比
7、一物体在距离地面高 h 的位置无初速度释放,不计空气阻力,经过 t 时间后落至地面,落到地面时的速度为 v ,则下列说法不正确的是( )
A.物体通过前半程和后半程所用时间之比为
B.物体通过 处的速度为
C.物体通过 处的速度为
D.物体经过前 和后 的位移之比为
8、(多选)有一串珠子(珠子可视为质点),穿在一根长 1.8m 的细线上,细线的首尾各固定 1 个珠子,中间还有 5 个珠子。从最下面的珠子算起,相邻两个珠子之间的距离依次为 5cm 、 15cm 、 25cm 、 35cm 、 45cm 、 55cm ,如图所示。某人向上提起细线的上端,让细线自由垂下,且第 1 个珠子紧贴水平桌面,松手后开始计时,若不计空气阻力, g 取 10m/s 2 ,假设珠子落到桌面上不再反弹,则第 2 、 3 、 4 、 5 、 6 、 7 个珠子( )
A.依次落到桌面上的速率之比为 1 : 2 : 3 : 4 : 5 : 6
B.落到桌面上的时间间隔相等
C.落到桌面上的时间间隔越来越大
D.第 4 个珠子落到桌面上的速率为 4m/s
9、(多选)科技馆中的一个展品如图所示,在较暗处有一个不断均匀滴水的水龙头,在一种特殊的间歇闪光灯的照射下,若调节间歇闪光时间间隔正好与水滴从A下落到B的时间相同,可以看到一种奇特的现象,水滴似乎不再下落,而仿佛是固定在图中的A、B、C、D四个位置不动,对出现的这种现象,下列描述正确的是()
A. 水滴在下落过程中通过相邻两点之间的时间满足tAB<tBC<tCD
B. 间歇发光的间隔时间是
C. 水滴在B、C、D点速度之比满足vB:vC:vD=1:4:9
D. 根据题目条件可以求得水滴在D点的速度
10、如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5、6…所示小球运动过程中每次曝光的位置.连续两次曝光的时间间隔均为,每块砖的厚度为。根据图中的信息,下列判断错误的是( )
A.位置“1”是小球释放的初始位置
B.小球做匀加速直线运动
C.小球下落的加速度为
D.小球在位置“4”的速度为
11、一颗小石头从某一高度处由静止自由下落,经过A点时的速度是10m/s,到达地面B点时的速度是30m/s..求:
(1)小石头下落时的高度;
小石头从A点运动到B点的时间和A、B间的距离.
12、如图所示,在汶川大地震中,一架直升飞机在灾区某地上空做定点空投救灾物资,已知由静止释放的一包物资,经5s刚好着地,忽略空气阻力的作用g=10 m/s2.求:
(1)释放后1s末物资速度大小.
(2)直升飞机距离地面的高度.
(3)物资落地前最后1s内的位移.
13、跳伞运动员做低空跳伞表演,当飞机离地面224m水平飞行时,运动员离开飞机在竖直方向做自由落体运动.运动一段时间后,立即打开降落伞,展伞后运动员以12.5m/s2的加速度匀减速下降,为了运动员的安全,要求运动员落地速度最大不得超过5m/s(取g=10m/s2).求:
(1)运动员展伞时,离地面的高度至少为多少?
(2)运动员在空中的最短时间为多少?
14、如图所示,一个可视为质点的小球从距地面125m高的A处开始自由下落,到达地面O点后经过地面反弹上升到最大高度为45m的B处,已知AO、OB在同一直线上,不计空气阻力,g=10m/s2,求:
(1)小球下落的时间为多少?小球从A点下落再反弹至B点全程位移为多少?
(2)小球经过地面反弹后瞬间的速度为多大?
(3)小球下落时最后1秒内的位移为多少?
15、有一种“傻瓜”相机的曝光时间(快门打开到关闭的时间)是固定不变的,为了估测相机曝光时间,有位同学提出了下述实验方案:他从墙上A点的正上方与A相距H=1.5m处,使一个小石子自由下落,对小石子拍照,得到如下图所示的照片,由于石子的运动,它在照片上留下一条模糊的径迹CD,已知每块砖的平均厚度是6cm。
请从上述信息和照片上选取估算相机曝光时间必要的物理量,用符号表示,如H等,推出计算曝光时间的关系式,并估算出这个“傻瓜”相机的曝光时间,要求保留一位有效数字。
答 案
1、【答案】AD
【解析】
【详解】
B.物体在第 5s 内的平均速度
B 错误;
C .根据自由落体规律
可得自由下落的加速度
C 错误;
A .物体在 2s 末的速度
A 正确;
D .体在 5s 内的位移
D 正确。
故选 AD 。
2、【答案】BD
【解析】
【详解】
A .根据
解得运动员双脚入水时的速度
A 错误;
B .根据
解得拍第二张照片时运动员的瞬时速度
B 正确;
D .运动员做自由落体运动,下落到距水面为 h 1 =8.2m 时,所需时间为 t ,则
下落到距水面为 h 2 =6.8m 时
解得
D 正确;
C .拍第二张照片时运动员下降的时间
解得
则排第三张时间
此时运动员下降的高度
第三张照片中运动员双脚离水面的高度
C 错误。
故选 BD 。
3、【答案】C
【解析】
【详解】
A .由于物体在第 1s 内下落的位移为 ,根据位移时间公式
解得物体下落的加速度为
A 错误;
B .根据速度时间公式,可得物体在 2s 末的速度为
B 错误;
C .根据位移时间公式,可得物体在第 2s 内下落的位移为
C 正确;
D .根据位移时间公式可得,物体下落的总位移为
D 错误。
故选 C 。
4、【答案】B
【解析】
【详解】
由速度位移公式,可得
解得下落高度为
ACD 错误, B 正确。
故选 B 。
5、【答案】ACD
【详解】
A .直尺下落的高度为 h ,根据
可得
则下落高度越大,用时越长,乙同学第一次的 “ 反应时间 ” 比第二次长,故 A 正确;
B .由 可得乙第一次抓住直尺时,直尺的速度为
故 B 错误;
C .若某同学的 “ 反应时间 ” 大于 0.4s ,则下落的高度
大于该直尺的长度,用该直尺将无法用上述方法测量他的 “ 反应时间 ” ,故 C 正确;
D .将计算出的反应时间对应到尺子的长度上时,则可用上述方法直接测出 “ 反应时间 ” ,故 D 正确。
故选 ACD 。
6、【答案】A
【详解】
C .自由落体运动位移时间关系有: ,得运动时间
三者运动时间
故 C 错误;
A .由上可得 ,因为三者同时到达地面,则 b 与 a 之间的时间差
c 与 b 的时间差
b 与 a 开始下落的时间差小于 c 与 b 开始下落的时间差,故 A 正确;
B .小球均做自由落体运动,根据 ,落地的速度之比为 ,故 B 错误;
D .三个小球运动的加速度均相同,与质量无关,故 D 错误.
故选 A .
7、【答案】D
【详解】
A .设全程高度为 h ,则由位移公式可知,
则前半程的时间
全程的时间
则后半程所用时间为
故前后半程内的时间之比为: 1 :( -1 );故 A 正确;
B .由
v 2 =2 gh
可得,通过 时的速度为
而落地时的速度
故
故 B 正确;
C .由
v=gt
可得,物体通过 时的速度
v ′ = g =
故 C 正确;
D .物体经过前 的位移
则后 的位移为 ;即物体经过前 和后 的位移之比为 1∶3 ,故 D 错误。
此题选择错误选项,故选 D 。
8、【答案】AB
【详解】
ABC .各珠子同时做自由落体运动,下降的位移之比为 1∶4∶9∶16∶25∶36 ;根据
知落地的时间之比为
1∶2∶3∶4∶5∶6
则各珠子落到桌面上的时间间隔相等,根据
知,依次落到桌面上的速率之比为
1∶2∶3∶4∶5∶6
故 AB 正确, C 错误;
D .第 4 个珠子距离桌面的高度为 45cm ,则
故 D 错误。
故选 AB 。
9、【答案】BD
【解析】由图可知,ABCD之间相邻两个点的间隔之比由上到下为1:3:5,故可知这是初速度为0的匀加速直线运动的相等时间内的位移之比,所以水滴在下落过程中通过相邻两点之间的时间满足tAB=tBC=tCD,选项A错误;根据xCD-xBC=gt2可计算出t=,选项B正确;水滴在B、C、D点速度之比满足vB:vC:vD=g×t:g×2t:g×3t=1:2:3,选项C错误;因为水滴在A点下落,故A点的速度为0,到D点时经过4t,则D点的速度可求,vD=g×4t,选项D正确。
10、【答案】A
11、【答案】
自由落体运动.
【分析】(1)根据自由落体运动求运动的下落高度
根据匀变速直线运动的速度公式求AB间的时间,速度位移关系求AB间的位移.
【解答】解(1)设小石头下落时的高度为H.由
得 H=45m
设小石头在A、B间运动的时间为t1,A、B间的距离为h.
由运动学公式
得:
由
得
答:(1)小石头下落时的高度45m;
小石头从A点运动到B点的时间2s和A、B间的距离40m.
【点评】熟练掌握自由落体运动的速度时间关系、速度位移关系是解决本题的关键.
12、【答案】
解:物资的下落看作自由落体运动。
(1)由
得:
(2)由
得:
(3)
得:
用其他方法解答正确同样得分。
13、【答案】
解:设运动员未开伞自由下落的时间为t1,开伞后做匀减速运动的时间为t2
以向下为正方向,则匀减速时的加速度为:a=﹣12.5m/s2
在临界情况下,运动员将以5m/s的速度着落.
所以有速度关系:vt=gt1+at2=10t1﹣12.5t2=5 …①
自由下落的高度:h1==5t12…②
展开伞时离地高度(即减速下落的高度):h2=gt1t2+=10t1t2﹣…③
位移关系:h1+h2=224 …④
联合①②③④式可解得:t1=5s,t2=3.6s,h1=125m,h2=99m.
所以运动员展开伞时离地高度至少应为99m
运动员在空中的最短时间是:t=t1+t2=8.6s
答:(1)运动员展开伞时,离地面的高度至少99m
(2)运动员在空中的最短时间是8.6s
14、【答案】
解:(1)由题给条件可得:h=125m,h1=45m
由公式可得:,
小球通过的位移为:x=h﹣h1=125m﹣45m=80m.
(2)由公式v2=2gh1可得:v=m/s=30m/s.
(3)小球下落时最后1秒的位移为:
.
答:(1)小球下落的时间为5s,小球从A点下落再反弹至B点全程位移为80m;
(2)小球经过地面反弹后瞬间的速度为30m/s;
(3)小球下落时最后1秒内的位移为45m.
15、【答案】
解析:设A、C两点间距离为H1,小石子做自由落体运动,落至C,所用时间t1,
有:;
设A、D两点间的距离为H2,小石子做自由落体运动,落至D点,所用时间为t2
有;
小石子从C点到D点所用的时间既相机的曝光时间
;
题目中给出每块砖的平均厚度是6cm,可得:H1=0.30m,H2=0.42m,H=1.5m,
带入上式中,可得曝光时间t=0.02s。
知识点总结
考点一、自由落体运动
1、定义:物体只在重力作用下从静止开始的运动叫自由落体运动。
2、条件:只受重力作用;初速度为0
3、运动性质
自由落体运动是初速度为零,加速度的匀加速直线运动,它是我们前面所学的匀变速直线运动的一个特例,其v-t图像是一条过原点的倾斜直线,斜率
4、对自由落体运动的理解
(1)自由落体是一种理想化模型,这种模型忽略了次要因素----空气阻力,突出了主要因素----重力。实际上,物体下落时由于受空气阻力的作用,并不做自由落体运动。但是,当空气阻力远小于物体的重力时,可以认为物体只受重力作用,此时物体由静止下落就可以看作自由落体运动。比如,在空气中石块的下落,在短时间内可以看作自由落体运动,而在空气中羽毛的下落不能看作自由落体运动。
(2)自由落体运动在其他星球上也可以发生,但物体下落时的加速度和在地球上的一般不同。
考点二、自由落体运动的实验探究
1、实验原理
重物拖着纸带竖直下落时,如果纸带阻力和空气阻力比重物的重力小得多,可以近似认为重物仅在重力作用下运动,根据打点计时器打出的纸带能分析和研究重物的运动规律。
2、实验器材
打点计时器(带导线)、纸带、复写纸、带铁夹的铁架台、几个质量不同的重物、夹子、低压交流电、毫米刻度尺
3、探究过程
(1)如图所示,将打点计时器竖直固定在铁架台上,连接好电路。
(2)把纸带穿过两个限位孔,下端用铁夹夹到重物上,让重物靠近打点计时器。
(3)用手捏住纸带上端把纸带拉成竖直状态,接通电源,松开纸带让重物自由下落,重物落地后立即关闭电源,打点计时器就在纸带上打下一系列的点。
(4)改变重物的质量,重复几次上面的实验,选取一条点迹清晰的纸带进行分析。
4、注意事项
(1)为了减少空气阻力的影响,重物应选密度大、体积小的物体,如铁锤等。
(2)打点计时器应竖直固定好。
(3)重物应靠近打点计时器释放,且要先接通打点计时器的电源,再放手让重物下落。
5、数据处理
(1)用刻度尺测量打点计时器打出的纸带上各点间的距离。
(2)用求出各点的瞬时速度,作v-t图像,图像是一条过原点的向上倾斜的直线,斜率表示加速度。
(3)根据计算加速度,判断运动性质。
6、实验结论
自由落体运动是初速度为零、加速度恒定(约为9.8,与物体的质量无关)的匀加速直线运动。
考点三、自由落体运动的规律
1、自由落体加速度g
(1)定义:在同一地点,一切物体在自由落体运动中的加速度都相同,这个加速度叫作自由落体加速度,又叫重力加速度,符号为g。自由落体加速度的方向总是竖直向下的。
(2)g的数值:在地球的同一个地方,g 的值不变,在地球不同地方g的值不相同。g值随高度增大而减小,随纬度增大而增大。在通常的计算中g取9.8m/s2 ,粗略计算时 取10m/s2
2、自由落体运动的特点与规律
(1)特点:自由落体运动是的匀加速直线运动。
(2)规律:
①速度公式位移公式:
②位移公式:
③速度与位移的关系式 (为物体下落的高度,不是距离地面的高度)。
3、自由落体运动的推论
(1)连续相等时间t内高度差:
(2)物体的平均速度:=
(3)第1个T内,第2个T内,第3个T内,···,第 个T内下落的高度之比:
下落连续相同的高度所用间之比:
考点四:计算重力加速度常见方法
方法一:利用相邻的、相等的时间间隔的位移差相等,且为一定值,即,则
方法二:可由位移公式求得。利用刻度尺量出从初始位置到某点的位移,若已知发生这段位移的时间,则。可以找多个点,多次求g值,再求平均值。
方法三:可利用速度公式求得。利用平均速度求某一点的瞬时速度,并已知自由下落的物体经过这一点的时间,则由解得,当然亦可多找点,多次求瞬时速度,多次求g值,再求平均值。
方法四:利用多次求得的瞬时速度,画出v-t图像,根据图像的斜率求得g。
方法五:用滴水法可以测定重力加速度的值。
方法是:在自来水龙头下面固定一块挡板A,使水一滴一滴连续地滴落到挡板上,如图所示,仔细调节水龙头,使得耳朵刚好听到前一个水滴滴在挡板上的声音的同时,下一个水滴刚好开始下落。首先量出水龙头口离挡板的高度h,再用停表计时。计时方法是:当听到某一水滴滴在挡板上的声音的同时,开启停表开始计时,并数“1”,以后每听到一声水滴声,依次
数“2,3,·..”,一直数到“n”,按下停表按钮停止时,读出停表的示数为
t。根据以上数据可求。
由上可知,相邻两滴水声的间隔就是水滴自由下落的时间,故,由得
题型总结:
1、(多选)一名宇航员在某星球上完成自由落体运动实验,让一个质量为 2kg 的小球从一定的高度自由下落,测得在第 5s 内的位移是 18m ,则( )
A.物体在 2s 末的速度是 8m/s
B.物体在第 5s 内的平均速度是 3.6m/s
C.物体自由下落的加速度是
D.物体在 5s 内的位移是 50m
2、(多选)跳水运动员训练时从十米跳台双脚朝下自由落下,某同学利用手机的连拍功能,连拍了多张照片。测得其中三张连续的照片中运动员双脚离水面的高度分别为 、 和 ,自由落体加速度 g 取 ,则( )
A.运动员双脚入水时的速度为
B.拍第二张照片时运动员的瞬时速度为
C.第三张照片中运动员双脚离水面的高度
D.手机连拍的时间间隔是 0.2s
3、一个物体做自由落体运动, 3s 末物体落地。若物体在第 1s 内下落的位移为 ,则( )
A.物体下落的加速度为
B.物体在 2s 末的速度为 20m/s
C.物体在第 2s 内下落的位移为
D.物体下落的总位移为
4、一个自由落体的物体,到达地面时的速度为 30m/s ,取 g =10m/s 2 ,则下落的高度为( )
A.40m B.45m C.60m D.65m
5、(多选)如图所示,甲同学拿着一把长 50cm 的直尺,乙同学把手放在 0 刻度线处准备抓尺,测反应时间。第一次乙同学抓住直尺位置的刻度值为 20cm ;重复实验,第二次手抓住直尺位置的刻度值为 10cm ,取 。下列说法正确的是( )
A.乙同学第一次的 “ 反应时间 ” 比第二次长
B.乙同学第一次抓住直尺之前的瞬间,直尺的速度约为
C.若某同学的“反应时间”大于,则用该直尺将无法用上述方法测量他的“反应时间”
D.若将尺子上原来的长度值改为对应的 “ 反应时间 ” 值,则可用上述方法直接测出“反应时间”
6、
15.
如图所示,在一个桌面上方有三个金属小球 a 、 b 、 c ,离桌面高度分别为 。若先后顺次释放 a 、 b 、 c ,三球刚好同时落到桌面上,不计空气阻力,则( )
A. b 与 a 开始下落的时间差小于 c 与 b 开始下落的时间差
B.三者到达桌面时的速度之比是 3∶2∶1
C.三者运动时间之比为 3∶2∶1
D.三个小球运动的加速度与小球受到的重力成正比,与质量成反比
7、一物体在距离地面高 h 的位置无初速度释放,不计空气阻力,经过 t 时间后落至地面,落到地面时的速度为 v ,则下列说法不正确的是( )
A.物体通过前半程和后半程所用时间之比为
B.物体通过 处的速度为
C.物体通过 处的速度为
D.物体经过前 和后 的位移之比为
8、(多选)有一串珠子(珠子可视为质点),穿在一根长 1.8m 的细线上,细线的首尾各固定 1 个珠子,中间还有 5 个珠子。从最下面的珠子算起,相邻两个珠子之间的距离依次为 5cm 、 15cm 、 25cm 、 35cm 、 45cm 、 55cm ,如图所示。某人向上提起细线的上端,让细线自由垂下,且第 1 个珠子紧贴水平桌面,松手后开始计时,若不计空气阻力, g 取 10m/s 2 ,假设珠子落到桌面上不再反弹,则第 2 、 3 、 4 、 5 、 6 、 7 个珠子( )
A.依次落到桌面上的速率之比为 1 : 2 : 3 : 4 : 5 : 6
B.落到桌面上的时间间隔相等
C.落到桌面上的时间间隔越来越大
D.第 4 个珠子落到桌面上的速率为 4m/s
9、(多选)科技馆中的一个展品如图所示,在较暗处有一个不断均匀滴水的水龙头,在一种特殊的间歇闪光灯的照射下,若调节间歇闪光时间间隔正好与水滴从A下落到B的时间相同,可以看到一种奇特的现象,水滴似乎不再下落,而仿佛是固定在图中的A、B、C、D四个位置不动,对出现的这种现象,下列描述正确的是()
A. 水滴在下落过程中通过相邻两点之间的时间满足tAB<tBC<tCD
B. 间歇发光的间隔时间是
C. 水滴在B、C、D点速度之比满足vB:vC:vD=1:4:9
D. 根据题目条件可以求得水滴在D点的速度
10、如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5、6…所示小球运动过程中每次曝光的位置.连续两次曝光的时间间隔均为,每块砖的厚度为。根据图中的信息,下列判断错误的是( )
A.位置“1”是小球释放的初始位置
B.小球做匀加速直线运动
C.小球下落的加速度为
D.小球在位置“4”的速度为
11、一颗小石头从某一高度处由静止自由下落,经过A点时的速度是10m/s,到达地面B点时的速度是30m/s..求:
(1)小石头下落时的高度;
小石头从A点运动到B点的时间和A、B间的距离.
12、如图所示,在汶川大地震中,一架直升飞机在灾区某地上空做定点空投救灾物资,已知由静止释放的一包物资,经5s刚好着地,忽略空气阻力的作用g=10 m/s2.求:
(1)释放后1s末物资速度大小.
(2)直升飞机距离地面的高度.
(3)物资落地前最后1s内的位移.
13、跳伞运动员做低空跳伞表演,当飞机离地面224m水平飞行时,运动员离开飞机在竖直方向做自由落体运动.运动一段时间后,立即打开降落伞,展伞后运动员以12.5m/s2的加速度匀减速下降,为了运动员的安全,要求运动员落地速度最大不得超过5m/s(取g=10m/s2).求:
(1)运动员展伞时,离地面的高度至少为多少?
(2)运动员在空中的最短时间为多少?
14、如图所示,一个可视为质点的小球从距地面125m高的A处开始自由下落,到达地面O点后经过地面反弹上升到最大高度为45m的B处,已知AO、OB在同一直线上,不计空气阻力,g=10m/s2,求:
(1)小球下落的时间为多少?小球从A点下落再反弹至B点全程位移为多少?
(2)小球经过地面反弹后瞬间的速度为多大?
(3)小球下落时最后1秒内的位移为多少?
15、有一种“傻瓜”相机的曝光时间(快门打开到关闭的时间)是固定不变的,为了估测相机曝光时间,有位同学提出了下述实验方案:他从墙上A点的正上方与A相距H=1.5m处,使一个小石子自由下落,对小石子拍照,得到如下图所示的照片,由于石子的运动,它在照片上留下一条模糊的径迹CD,已知每块砖的平均厚度是6cm。
请从上述信息和照片上选取估算相机曝光时间必要的物理量,用符号表示,如H等,推出计算曝光时间的关系式,并估算出这个“傻瓜”相机的曝光时间,要求保留一位有效数字。
答 案
1、【答案】AD
【解析】
【详解】
B.物体在第 5s 内的平均速度
B 错误;
C .根据自由落体规律
可得自由下落的加速度
C 错误;
A .物体在 2s 末的速度
A 正确;
D .体在 5s 内的位移
D 正确。
故选 AD 。
2、【答案】BD
【解析】
【详解】
A .根据
解得运动员双脚入水时的速度
A 错误;
B .根据
解得拍第二张照片时运动员的瞬时速度
B 正确;
D .运动员做自由落体运动,下落到距水面为 h 1 =8.2m 时,所需时间为 t ,则
下落到距水面为 h 2 =6.8m 时
解得
D 正确;
C .拍第二张照片时运动员下降的时间
解得
则排第三张时间
此时运动员下降的高度
第三张照片中运动员双脚离水面的高度
C 错误。
故选 BD 。
3、【答案】C
【解析】
【详解】
A .由于物体在第 1s 内下落的位移为 ,根据位移时间公式
解得物体下落的加速度为
A 错误;
B .根据速度时间公式,可得物体在 2s 末的速度为
B 错误;
C .根据位移时间公式,可得物体在第 2s 内下落的位移为
C 正确;
D .根据位移时间公式可得,物体下落的总位移为
D 错误。
故选 C 。
4、【答案】B
【解析】
【详解】
由速度位移公式,可得
解得下落高度为
ACD 错误, B 正确。
故选 B 。
5、【答案】ACD
【详解】
A .直尺下落的高度为 h ,根据
可得
则下落高度越大,用时越长,乙同学第一次的 “ 反应时间 ” 比第二次长,故 A 正确;
B .由 可得乙第一次抓住直尺时,直尺的速度为
故 B 错误;
C .若某同学的 “ 反应时间 ” 大于 0.4s ,则下落的高度
大于该直尺的长度,用该直尺将无法用上述方法测量他的 “ 反应时间 ” ,故 C 正确;
D .将计算出的反应时间对应到尺子的长度上时,则可用上述方法直接测出 “ 反应时间 ” ,故 D 正确。
故选 ACD 。
6、【答案】A
【详解】
C .自由落体运动位移时间关系有: ,得运动时间
三者运动时间
故 C 错误;
A .由上可得 ,因为三者同时到达地面,则 b 与 a 之间的时间差
c 与 b 的时间差
b 与 a 开始下落的时间差小于 c 与 b 开始下落的时间差,故 A 正确;
B .小球均做自由落体运动,根据 ,落地的速度之比为 ,故 B 错误;
D .三个小球运动的加速度均相同,与质量无关,故 D 错误.
故选 A .
7、【答案】D
【详解】
A .设全程高度为 h ,则由位移公式可知,
则前半程的时间
全程的时间
则后半程所用时间为
故前后半程内的时间之比为: 1 :( -1 );故 A 正确;
B .由
v 2 =2 gh
可得,通过 时的速度为
而落地时的速度
故
故 B 正确;
C .由
v=gt
可得,物体通过 时的速度
v ′ = g =
故 C 正确;
D .物体经过前 的位移
则后 的位移为 ;即物体经过前 和后 的位移之比为 1∶3 ,故 D 错误。
此题选择错误选项,故选 D 。
8、【答案】AB
【详解】
ABC .各珠子同时做自由落体运动,下降的位移之比为 1∶4∶9∶16∶25∶36 ;根据
知落地的时间之比为
1∶2∶3∶4∶5∶6
则各珠子落到桌面上的时间间隔相等,根据
知,依次落到桌面上的速率之比为
1∶2∶3∶4∶5∶6
故 AB 正确, C 错误;
D .第 4 个珠子距离桌面的高度为 45cm ,则
故 D 错误。
故选 AB 。
9、【答案】BD
【解析】由图可知,ABCD之间相邻两个点的间隔之比由上到下为1:3:5,故可知这是初速度为0的匀加速直线运动的相等时间内的位移之比,所以水滴在下落过程中通过相邻两点之间的时间满足tAB=tBC=tCD,选项A错误;根据xCD-xBC=gt2可计算出t=,选项B正确;水滴在B、C、D点速度之比满足vB:vC:vD=g×t:g×2t:g×3t=1:2:3,选项C错误;因为水滴在A点下落,故A点的速度为0,到D点时经过4t,则D点的速度可求,vD=g×4t,选项D正确。
10、【答案】A
11、【答案】
自由落体运动.
【分析】(1)根据自由落体运动求运动的下落高度
根据匀变速直线运动的速度公式求AB间的时间,速度位移关系求AB间的位移.
【解答】解(1)设小石头下落时的高度为H.由
得 H=45m
设小石头在A、B间运动的时间为t1,A、B间的距离为h.
由运动学公式
得:
由
得
答:(1)小石头下落时的高度45m;
小石头从A点运动到B点的时间2s和A、B间的距离40m.
【点评】熟练掌握自由落体运动的速度时间关系、速度位移关系是解决本题的关键.
12、【答案】
解:物资的下落看作自由落体运动。
(1)由
得:
(2)由
得:
(3)
得:
用其他方法解答正确同样得分。
13、【答案】
解:设运动员未开伞自由下落的时间为t1,开伞后做匀减速运动的时间为t2
以向下为正方向,则匀减速时的加速度为:a=﹣12.5m/s2
在临界情况下,运动员将以5m/s的速度着落.
所以有速度关系:vt=gt1+at2=10t1﹣12.5t2=5 …①
自由下落的高度:h1==5t12…②
展开伞时离地高度(即减速下落的高度):h2=gt1t2+=10t1t2﹣…③
位移关系:h1+h2=224 …④
联合①②③④式可解得:t1=5s,t2=3.6s,h1=125m,h2=99m.
所以运动员展开伞时离地高度至少应为99m
运动员在空中的最短时间是:t=t1+t2=8.6s
答:(1)运动员展开伞时,离地面的高度至少99m
(2)运动员在空中的最短时间是8.6s
14、【答案】
解:(1)由题给条件可得:h=125m,h1=45m
由公式可得:,
小球通过的位移为:x=h﹣h1=125m﹣45m=80m.
(2)由公式v2=2gh1可得:v=m/s=30m/s.
(3)小球下落时最后1秒的位移为:
.
答:(1)小球下落的时间为5s,小球从A点下落再反弹至B点全程位移为80m;
(2)小球经过地面反弹后瞬间的速度为30m/s;
(3)小球下落时最后1秒内的位移为45m.
15、【答案】
解析:设A、C两点间距离为H1,小石子做自由落体运动,落至C,所用时间t1,
有:;
设A、D两点间的距离为H2,小石子做自由落体运动,落至D点,所用时间为t2
有;
小石子从C点到D点所用的时间既相机的曝光时间
;
题目中给出每块砖的平均厚度是6cm,可得:H1=0.30m,H2=0.42m,H=1.5m,
带入上式中,可得曝光时间t=0.02s。
