探索规律[上学期]

课件16张PPT。探索规律 小时侯我们都玩过搭积木的
游戏，今天我们不妨重拾童年乐
趣，利用火柴棒搭建一些常见的
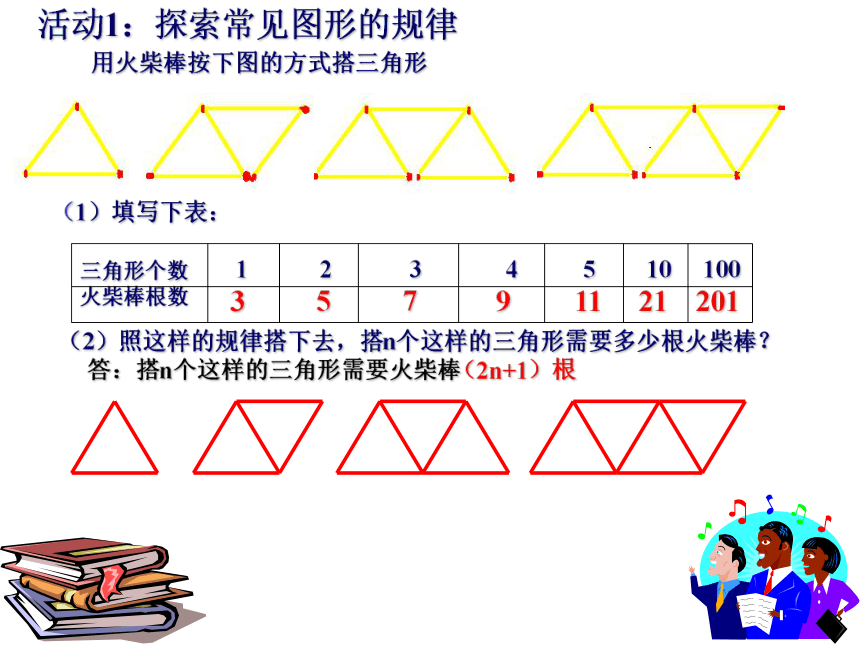
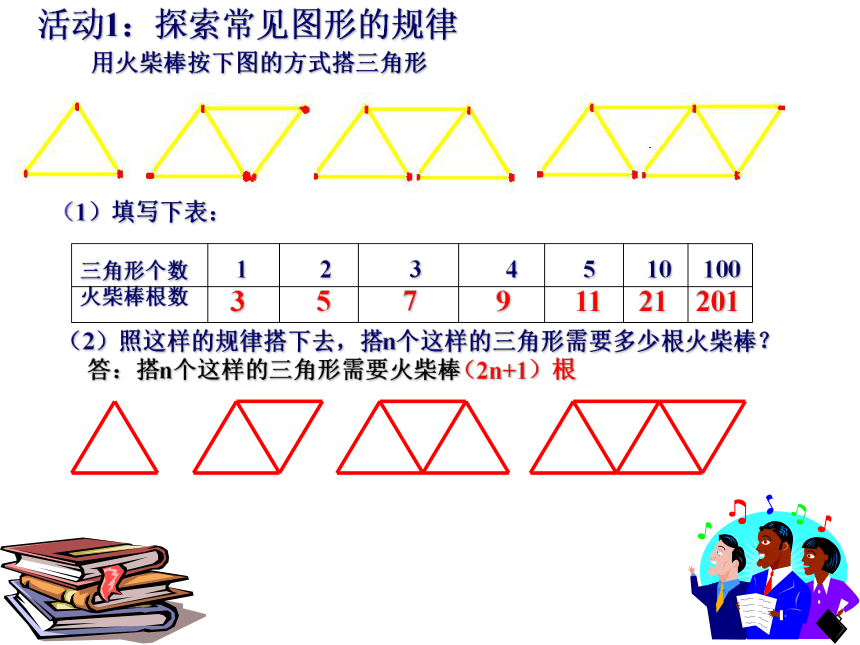
图形，探索数学规律。活动1：探索常见图形的规律
用火柴棒按下图的方式搭三角形 （2）照这样的规律搭下去，搭n个这样的三角形需要多少根火柴棒？（1）填写下表：三角形个数 1 2 3 4 5
火柴棒根数511397（2n+1）根答：搭n个这样的三角形需要火柴棒1010021201活动1：探索常见图形的规律
用火柴棒按下图的方式搭三角形 （2）照这样的规律搭下去，搭n个这样的三角形需要多少根火柴棒？（1）填写下表：三角形个数 1 2 3 4 5
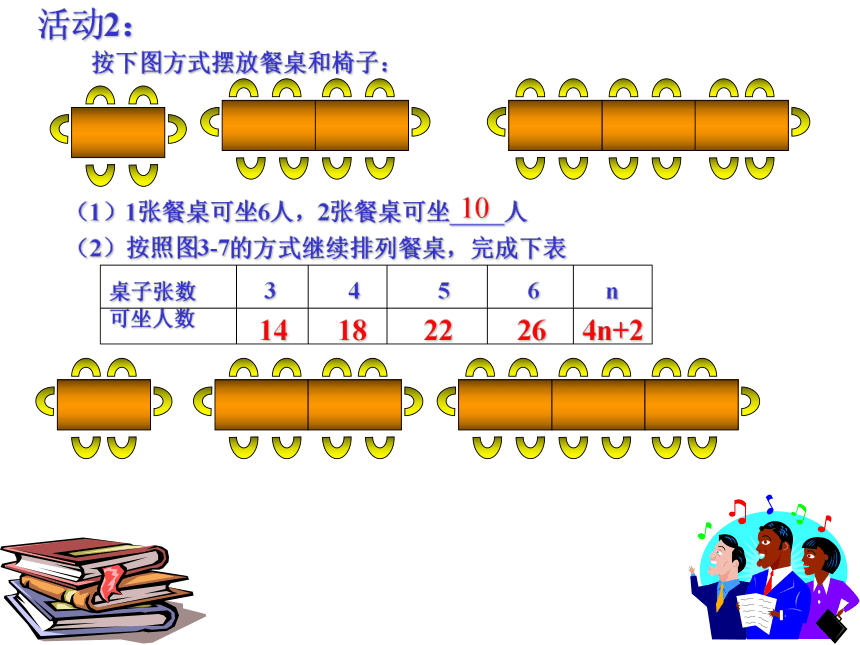
火柴棒根数511397（2n+1）根答：搭n个这样的三角形需要火柴棒1010021201探索规律的一般步骤1、寻找数量关系。 2、用代数式表示规律。3、验证规律。活动2：
按下图方式摆放餐桌和椅子： （2）按照图3-7的方式继续排列餐桌，完成下表（1）1张餐桌可坐6人，2张餐桌可坐 人18101426224n+2 (1)日历图的套色方框中的9个数之和与该方框正中间的数有
什么关系?
2+3+4+9+10+11+16+17+18=90(9个数之和为 90 , 是中间的数10的9倍)活动3:(4)你还能发现这样的方框中9个数之间的其他关系吗?用代
数式表示. (2)这个关系对其他这样的方框成立吗?你能用代数式表示这
个关系吗?
什么关系?
(3)这个关系对任何一个月的日历能成立吗?为什么?
(9个数之和为 90 , 是中间的数10的9倍)(1)日历图的套色方框中的9个数之和与该方框正中间的数有(3)答: 因为这9个数可以表示为 m-8 m-7 m-6 m+8 m+7 m+6 m-1 m+1（若用m表示正中间的数，则方框中9个数的和等于9m）是，活动4：
将一张长方形的纸对折，如右图所示可
得到一条折痕。继续对折，对折时每次折痕
与上次的折痕保持平行。连续对折1,2,3,4,5次
后分别可得到几条折痕？ 1371531
如果对折6,10,100
次呢？ 1张2张4张8张16张32张------活动4：
将一张长方形的纸对折，如右图所示可
得到一条折痕。继续对折，对折时每次折痕
与上次的折痕保持平行。连续对折1,2,3,4,5次
后分别可得到几条折痕？ 对折100次------- 条折痕对折n次------- 条折痕137153163对折6次------- 条折痕对折10次------- 条折痕=63
如果对折6,10,100
次呢？ 对折n 次呢？ 活动4：
将一张长方形的纸对折，如右图所示可
得到一条折痕。继续对折，对折时每次折痕
与上次的折痕保持平行。连续对折1,2,3,4,5次
后分别可得到几条折痕？ 对折100次------- 条折痕对折n次------- 条折痕137153163对折6次------- 条折痕对折10次------- 条折痕=63
如果对折6,10,100
次呢？ 对折n 次呢？ 练习：
四棱柱有几个顶点，几条棱，几个面？五棱柱呢？
六棱柱呢？十棱柱呢？ n棱柱呢？81210202n12151830 3n67812n+2练习：
用木棒按下图的方式搭正方形 （2）照这样的规律搭下去，搭n个这样的正方形需要多少根木棒？（1）填写下表：正方形个数 1 2 3 4 5
木棒根数71641310（3n+1）根答：搭n个这样的正方形需要木棒1010031301小 结 其实在我们周围的生活中存
在着很多很多的数学信息，今天
我们就利用数学知识发现了很多
身边事物所存在的数学规律。希
望同学们做生活的有心人，继续
去探索周围生活中的数学规律。 一般步骤:
1.寻找数量关系 2.用代数式表示规律 3.验证规律作 业 观察生活，编一道探索数学规律
的题目。