3.6探索规律[上学期]

课件17张PPT。3.6探索规律綦江中学 罗晓炜
2005、10 2005年10月 月历上黄色方框中的9个数之和与该方框正中间的数有什么关系？ 这一关系对任何一个月的月历都成立吗？为什么？
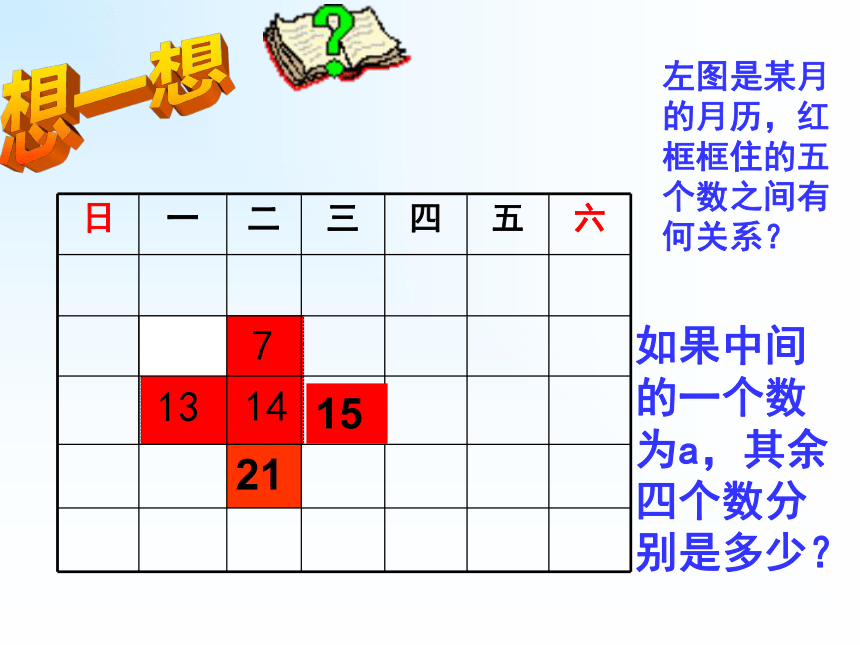
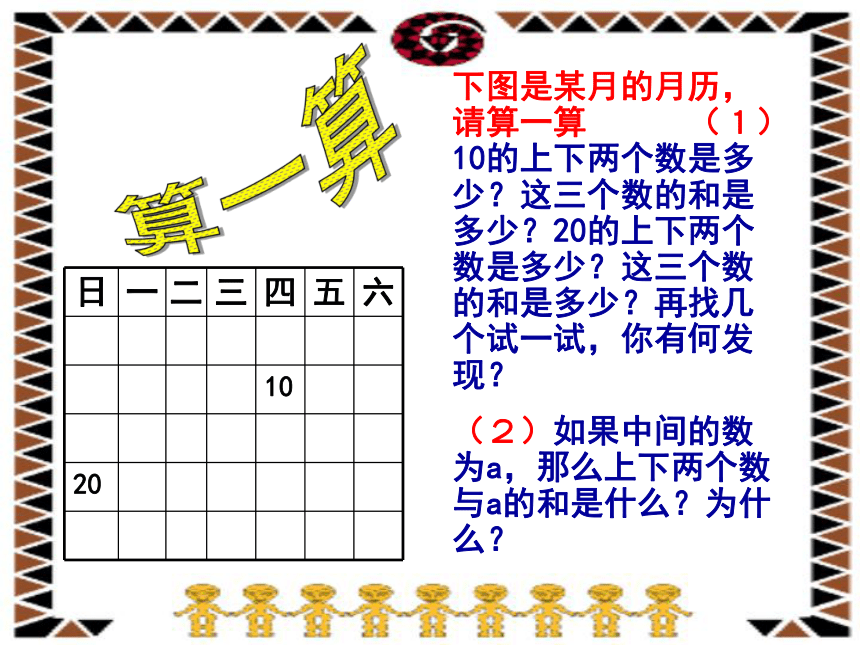
（提示：用代数式及合并同类项的知识解决） 发现探究月历中都有哪些规律？ n-8 n-7 n-6 n+8 n+7 n+6 n-1 n+1a+1aa+7a+8？？？71314想一想左图是某月的月历，红框框住的五个数之间有何关系？如果中间的一个数为a，其余四个数分别是多少？2115下图是某月的月历，请算一算 （１）10的上下两个数是多少？这三个数的和是多少？20的上下两个数是多少？这三个数的和是多少？再找几个试一试，你有何发现？ 　　　　　　　
（２）如果中间的数为a，那么上下两个数与a的和是什么？为什么？
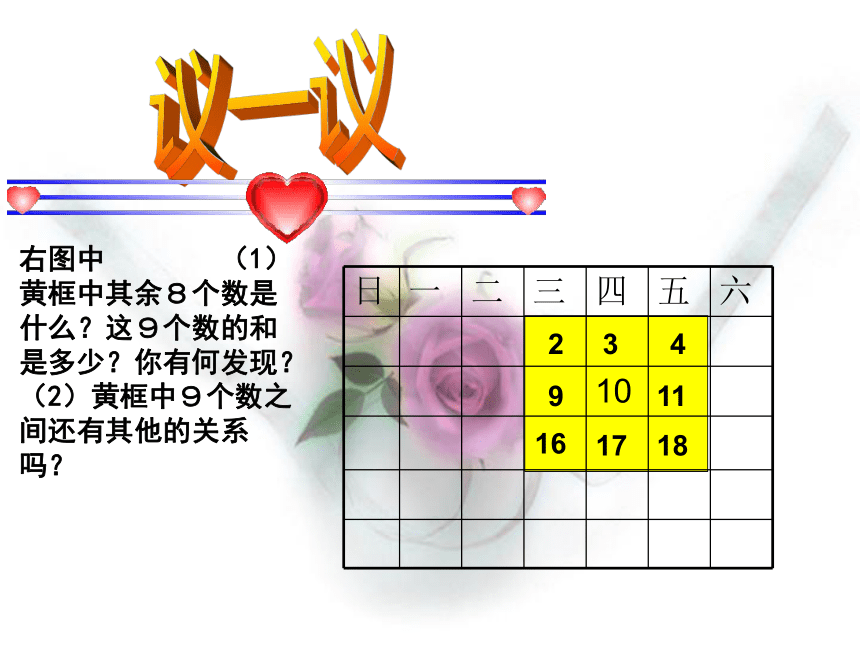
算一算右图中　　　 （1）黄框中其余８个数是什么？这９个数的和是多少？你有何发现？　　 （2）黄框中９个数之 间还有其他的关系 吗？议一议 2 16 3 9 11 17 18 4数字之间的关系1、前后两数之间相差1，上下两数之间相差7；2、米字型的四条直线中的三个数的平均数都等于中间这个数10，
因此这9个数的和是9×10＝90。议一议：研究其它月份：这样的方框中的数字关系也成立吗？这样存在的普遍规律，你能用数学方法来解释吗？若中间这个数为a，则这9个数的和是多少，另8个数怎么表示?若第1个数为a呢？若第1个数为a呢？另8个数如何表示？a+1a-8a-7a-6a+7a+6a+8a+1a+2a+7a+8a+9a+14a+15a+169aa-19(a+8)若中间这个数为a，另8个数如何表示？则这9个数的和为 ＿＿，则这9个数的和为 ＿＿ ，试一试 将一张纸连续对折，每一次的折痕都与第一次的折痕平行，对折2次后，纸为几层?折一折，试一试。可以得到几条折痕? 3次呢? 10次呢? 对折n次呢？对折次数与所得折痕数的变化关系表：２８１３７1516４-1做一做餐桌摆法一 如图摆放餐桌和凳子：
（１）１张餐桌可坐６人，２张餐桌可坐———人。3张餐桌呢？　　　　　（２）完成下表　　　　　　　　　
6101418…4n+2餐桌的摆法二：（填表）若按照上图的摆法摆放餐桌和凳子，完成下表： 6 8 102n+4 变式问题： 在桌数相同时，哪一种摆法容纳的人数更多？ 探索问题：有3张桌子,可以坐多少人？ 辅助练习：按规律填空：
① 2，4，6，8， ，12，14，…
②2，4，8， ，32，64，…
③1，3，7， ，21，…思考说一说你对探索规律方面有何收获?感悟与收获??(1)? 探索对象—事物间的数量关系
(2)??探索过程—收集、观察、分析数据，从多个角度用语言、表格或符号描述规律，代数式运算验证规律
?(3) 探索目的—用于计算或推测
再见！