探索规律[上学期]

课件17张PPT。《数学》(七年级 上册)探索规律(1)第三章 字母表示数6一首唱不完的儿歌一首唱不完的儿歌现实生活中有很多的规律性的东西，都可以用数学式子表示出来！1 只青蛙1 张嘴，2 只眼睛 4 条腿，1 声扑通跳下水； 2 只青蛙2 张嘴，4 只眼睛8 条腿，2 声扑通跳下水； 3 只青蛙3 张嘴，6 只眼睛12 条腿，3 声扑通跳下水；······ ······ 你能用代数式表示这首儿歌吗？ n 只青蛙 张嘴，
只眼睛， 条腿，
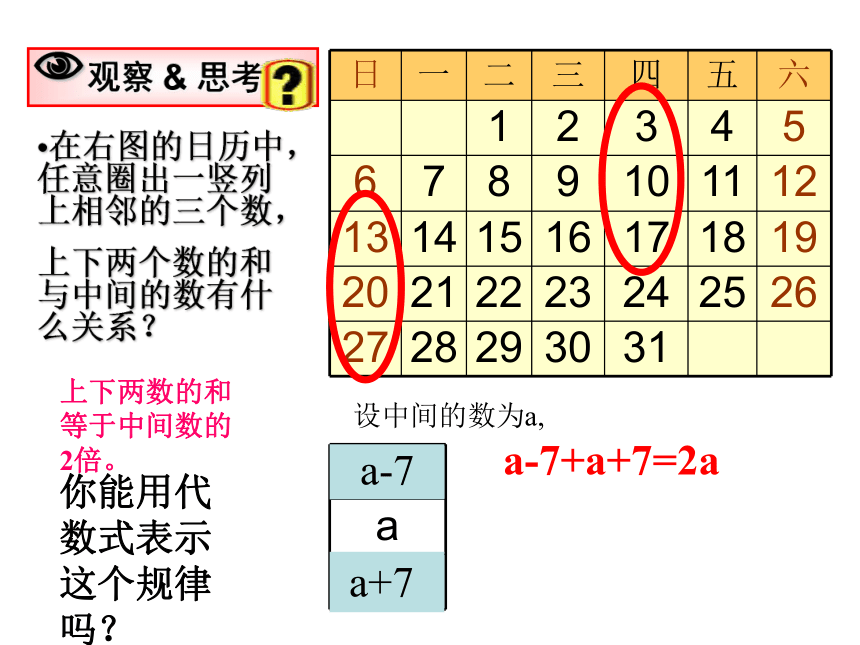
声扑通跳下水。n2n4nn 规律是客观存在的，让我们一起走进丰富的生活世界，去寻求数学真谛！探索规律在右图的日历中，任意圈出一竖列上相邻的三个数，
上下两个数的和与中间的数有什么关系？a-7+a+7=2a a-7 a+7上下两数的和等于中间数的2倍。你能用代数式表示这个规律吗？设中间的数为a,从日历中你能发现一些什么呢？首
先请看，我用一个矩形框框住四个
数如图，那么这四个数之间有些什
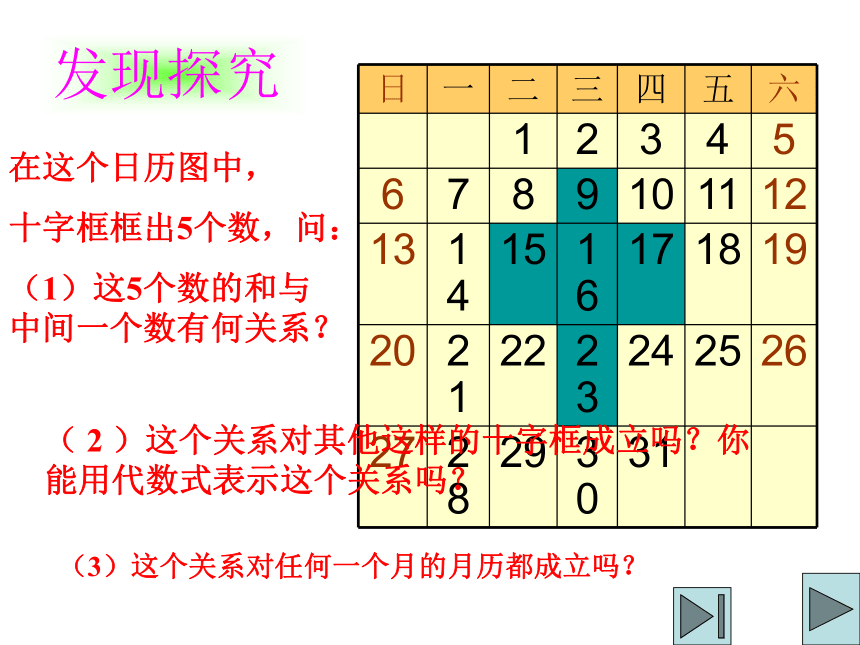
么关系呢？在这个日历图中，
十字框框出5个数，问：
（1）这5个数的和与中间一个数有何关系？（ 2 ）这个关系对其他这样的十字框成立吗？你能用代数式表示这个关系吗？
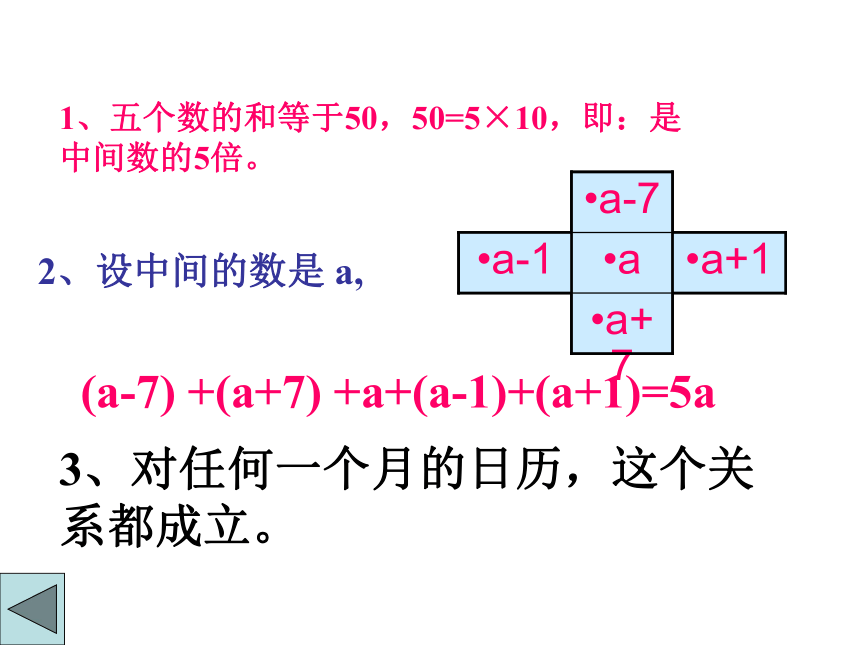
（3）这个关系对任何一个月的月历都成立吗？发现探究1、五个数的和等于50，50=5×10，即：是中间数的5倍。2、设中间的数是 a,3、对任何一个月的日历，这个关系都成立。
(a-7) +(a+7) +a+(a-1)+(a+1)=5a3.在 H 形区域中,7个数的和等于正中心数的7倍.
若设中心数为a, 则这七个数之和为：
(a-8)+(a-1)+(a+6)+a+(a- 6)+(a+1)+(a+8)=7a
4. 在w形区域中,七个数的和等于中心数的7倍.
若设中心数为a,则这七个数之和为:
(a-10)+(a-2)+(a+6)+(a+8)+(a+2)+(a-4)+a=7a
日 历 中 的 数 字 规 律 若设套色方框中正中间的数为 a ，你能用a 表示相邻的日期吗？这九个数可表示为：a－1a + 1a－7a + 7a－8a－6a + 6a + 8 将这九个数相加，正好等于9a 。 利用字母表示数与运算，可从一般角度来验证所发现的规律。日 历 中 的 数 字 规 律 a－1a－7a + 7a－8a－6a + 6a + 8a + 1 各行三数之和都是正中间的数的 。3 倍 随堂练习— 折 纸 问 题 将一张长方形的纸对折，如图所示可得到一条折痕。② 对折次数与所得层数的变化关系表：对折时每次折痕与上一次的折痕保持平行。 连续对折 6 次后，可以得到几条折痕？如果对折 10 次呢？如果对折 n 次呢？?思路启迪 ? 可从具体的、简单的对折次数入手，寻找所得折痕数与对折次数的变化关系：13715…24816…212223242n2n－126－1210－12n－1P111—1思路启迪 ? 可从具体的、简单的对折次数入手，寻找 所得折痕数与对折次数的变化关系. 13715…24816…212223242n2n－1 将一张长方形的纸对折，如右图所示可得到一条折痕，继续对折，对折时每次折痕与上次的折痕保持平行，连续对折n次后，可以得到多少条折痕？折 纸 问 题谁能算出：1+2+22+23+24+……2n=？
我们这节学到了什么？ 请同学们回顾本节课学习了哪些知识.
获得了哪些有指导意义的结论? 1、现实生活中有很多规律性的东西，都可以用数学式子表示出来！ 日历中的数字规律、日历中的方阵图。折纸问题. 2、利用字母表示数与运算，
可从一般角度来验证所发现的规律。
探索规律的一般步骤：猜 想 规 律表 示 规 律验 证 规 律具 体 问 题观 察 特 例成立得出结论头 回新 重索 探探索规律的一般步骤1、寻找数量关系。 2、用代数式表示规律。3、验证规律。根据探索规律的一般步骤完成学生学习支持材料任务中的任务二。愿您勇于探索永攀高峰GOOD BAY