探索规律[上学期]

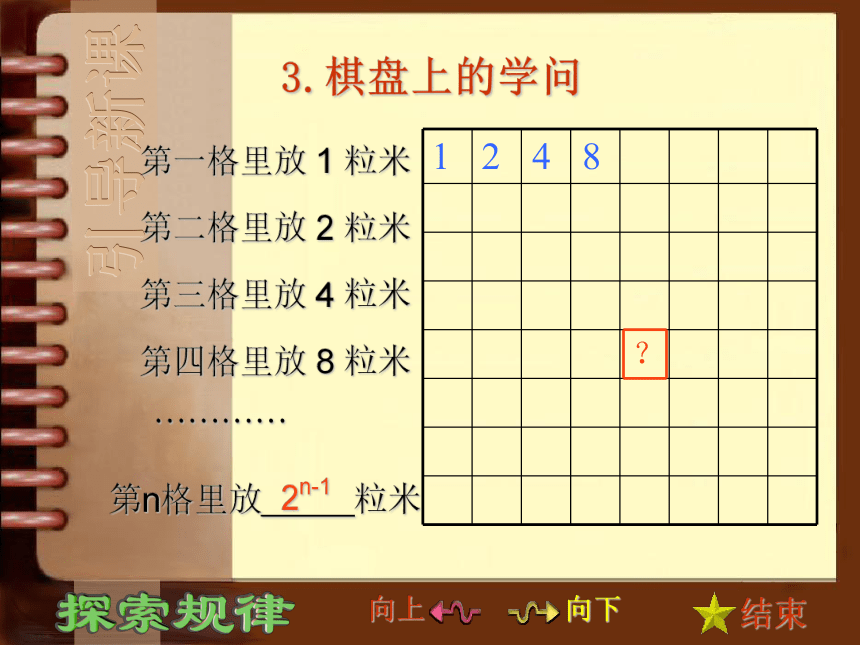
课件38张PPT。探索规律北师大版《数学》七年级（上）探索规律北师大版《数学》七年级（上）引导新课探索规律北师大版《数学》七年级（上）问题探究探索规律北师大版《数学》七年级（上）课内小结探索规律北师大版《数学》七年级（上）训练反馈 数学世界中充满着奥秘，这就需要我们去探索并认识它们的规律。——老师寄语引导新课 联欢会上，小明按照4个红球、3个黄球、2个绿球的顺序把气球串起来装饰会场，第52个气球是什么颜色？1.气球的颜色？2.唱不完的儿歌1只青蛙1张嘴，2只眼睛4条腿，1声扑通跳下水。2只青蛙2张嘴，4只眼睛8条腿，2声扑通跳下水。3只青蛙3张嘴，6只眼睛12条腿，3声扑通跳下水。…………n只青蛙n张嘴,2n只眼睛4n条腿,n声扑通跳下水。 一首永远唱不完的儿歌，你能用字母表示这首儿歌吗？…………引导新课引导新课3.棋盘上的学问1842第n格里放 粒米2n-1
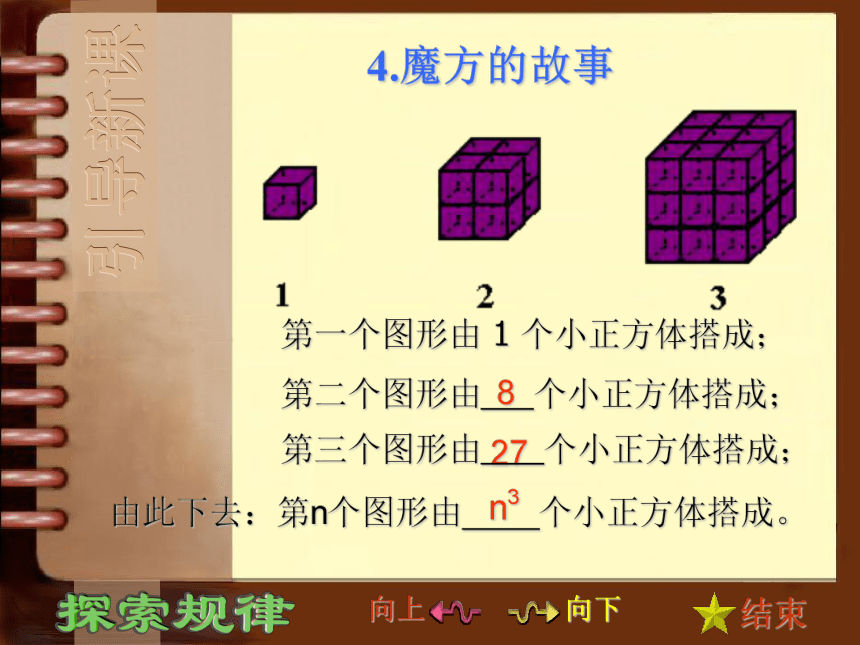
第四格里放 8 粒米第三格里放 4 粒米第二格里放 2 粒米第一格里放 1 粒米…………278n34.魔方的故事第一个图形由 1 个小正方体搭成；第二个图形由 个小正方体搭成；第三个图形由 个小正方体搭成；由此下去：第n个图形由 个小正方体搭成。引导新课问题探究1、探索规律即根据题目的条件（包括有规律算式、图表、图形等信息），从简单或特殊情况入手，进行归纳，并大胆猜想探索，得出结论，再通过具体验证而获得规律的过程。 现阶段，虽然我们不能在理论上加以证明许多猜想，但我们可通过特例初步获得验证。2、探索规律的一般步骤和方法特殊入手一般结论个例验证探索探索规律问题探究 图中每个图案是由若干盆花组成的形为三角形的图案，每条边（包括两个顶点）有n（n>1）盆花，每个图案花盆的总数是S。找出规律推断，S与n的关系式。盆景图案中的规律n=2 S=3n=3 S=6n=4 S=9探索1分析1除第一行和最后一行外，其余各行都有2只花盆，故计算得S=1+2(n-2)+n=3n-3问题探究从每边的个数环形数出来，
当n=2时，S=2+1+0=3
当n=3时，S=3+2+1=6
当n=4时，S=4+3+2=9
……
每条边上有n个花盆时，S=n+(n-1)+(n-2)=3n-3分析2分析3列表发现n和S的关系问题探究 将一张长方形的纸对折，可得到一条折痕，继续对折，对折时每次折痕与上次的折痕保持平行，连续对折6次后，可以得到 条折痕;如果对折10次后，可以得到 条折痕；如果对折n次，可以得到 条折痕。 对折长方形纸的规律探索26310232n-1问题探究通过上述折纸问题的实验，继续解决下列问题。1、对折次数与所得单层面积的变化关系：2、对折次数与所得层数的变化关系：3、平行对折次数与所得折痕数的变化关系：拓展问题探究1张长方形桌子可坐6人2张桌子可坐 人按照这样的方式继续排列桌子，完成下表.10餐桌椅摆放中的规律探索3问题探究若按下图方式摆放桌椅呢？拓展问题探究1、你发现日历表中的数与数之间有哪些关系？下面是2004年六月份的日历表：日历表中数的规律探索4问题探究2、在这个日历表中，十字框出5个数，问：（2）这个关系对其他这样的十字框成立吗？你能用代数式表示这个关系吗？（3）这个关系对任何一个月的日历成立吗？为什么？（1）日历图的套边方框中5个数之间有哪些关系？这五个数的和与中间一个数有何关系？问题探究3、在这个日历表中，正方形套边框出9个数，问：（1）正方形套边方框中的9个数之和与该方框正中间的数有什么关系？（2）这个关系对其他的方框成立吗？你能用代数式表示这个关系吗？（3）这个关系对任何一个月的日历都成立吗？为什么？（4）你还能发现这样的方框中9个数之间的其他关系吗？用代数式表示。问题探究 4、将前述日历表改成自然数1—1001，按下表排列成一个长方形阵列，用一个正方形框出9个数，要使这个正方形框出的9个数之和分别等于（1）1998；（2）2000；（3）2004，是否可能？若可能，求出框中最大数和最小数。若不可能，说明理由。?
拓展问题探究 5、若将自然数1—1001阵列，用一个正方形框出16个数，这16个数的和有何特殊关系吗？你能用代数式说明这个关系吗？框出的16个数之和能否等于（1）1998；（2）2000；（3）2004，是否可能？若可能，求出框中最大数和最小数。若不可能，说明理由。拓展课内小结1、探索规律的常用方法：2、日历表中的数与数之间的特殊关系。3、用数学方法探索身边的数学问题中的规律，你有哪些收获？课内小结特殊——一般——特殊。训练反馈1、观察下面的几个算式，你发现什么规律？12=1112=1211112=1232111112=1234321利用上面的规律，算出111112= .123454321训练反馈2、观察下面的几个算式，你发现什么规律？1+2+1=41+2+3+2+1=91+2+3+4+3+2+1=161+2+3+4+5+4+3+2+1=25…………利用上面的规律，请你迅速算出
1+2+3+……+99+100+99+……+3+2+1= 。 1002训练反馈3、观察下列各式：
12+1=1×2 22+2=2×3 32+3=3×4……
请你将猜想到的规律用自然数n（n≥1）表示出来 。4、选择题:观察下列各式，你会发现规律( )
3×5=15，而15=42-1；5×7=35，而35=62-1n(n+2)=(n+1)2-1 (B) n(n+2)=n2-1
(C) n(n+2)=(n-1)2-1 (D) n(n+2)=(n-2)2-1 n2+n=n(n+1)A训练反馈5、商店出售一种瓜子,数量x与售价c之间的关系如下表:表内售价栏中的0.05是塑料袋的价钱. 怎样用含x的代数式表示c呢?答案：c=0.009x+0.05训练反馈6、用游戏棒按从左到右的方式搭三角形，如此搭下去，填写下表中对应三角形所需要游戏棒的根数。训练反馈7、阅读理解：你能比较两个数20032004和20042003的大小吗？
为了解决这个问题，我们先把它抽象成数学问题，写出它的一般形式，即比较nn+1和(n+1)n的大小（n是自然数），然后我们分析n=1，n=2，n=3，……，从这些简单情形入手，发现规律，经过归纳、猜想得出结论。
（1）通过计算，比较下列各组中两个数的大小（在空格中填写“<”、“=”、“>”号）
①12 21；②23 32；③34 43；④45 54；⑤56 65。
（2）从第（1）题的结果经过归纳，可以猜想n n+1和(n+1)n的大小关系式是 。
（3）根据上面归纳猜想得到的一般结论，比较下列两数的大小：20032004 20042003.<<>>>n n+1>(n+1)n (n≥3)>布置作业3、现有一列数：2、4、8、16、□、64、128、……横线上“□”是 ？第n个数可表示为 ？4、你喜欢吃拉面吗？拉面馆的师傅用一根很粗的面条，把两头捏在一起拉伸，再捏合，再拉伸，反复几次，就把这根很粗的面条拉成了许多细面条，这样捏合到第 次后可拉出128根面条。必做题2、课本P. 113 做一做1、课本P.112-113 习题3.7、习题3.8布置作业5、如图：工地上有一堆圆形钢管，第一层有2根，第二层3根，第三层4根，……你能说出第八层有几根吗？第n层呢？布置作业1、观察算式:选做题布置作业2. 一批小球按下面的方法堆放你知道第(n)堆有多少个小球吗？如果不知道，想一想上一题的做法，这可能对你有启示。布置作业3、能否用6根火柴棒搭4个完全一样的三角形？把这个方法推广引伸下怎么样，并偿试完成填表。布置作业1、观察下面表格中数的排列规律,在空格处填上适当的数:思考题布置作业2、快餐厅每间都是正方形，要在每间餐厅内摆放一批如图所示的餐桌椅，同时安排40人就餐，请设计一种桌椅摆放方案，使没有剩余桌椅（要求选用图中的摆放方式），请画出你满意的设计图。开放性设计活动