探索规律[上学期]

课件13张PPT。比
一
比看谁找得快（1）1，2，3，4，5，6 ， _____，
8，9… 510105 （2）1，3，5，7，9，_________,13,15…（3）2，4，6，8，10，________,14，16…（4）3，6，9，12，……，_________(第n项)（5）711123n
探索规律日历中有哪些规律呢（1）横行相邻各数日期总是差1；
（2）竖列相邻各数总是差7；
（3）从上往下、从左到右的对角线上相邻各数总是差8；
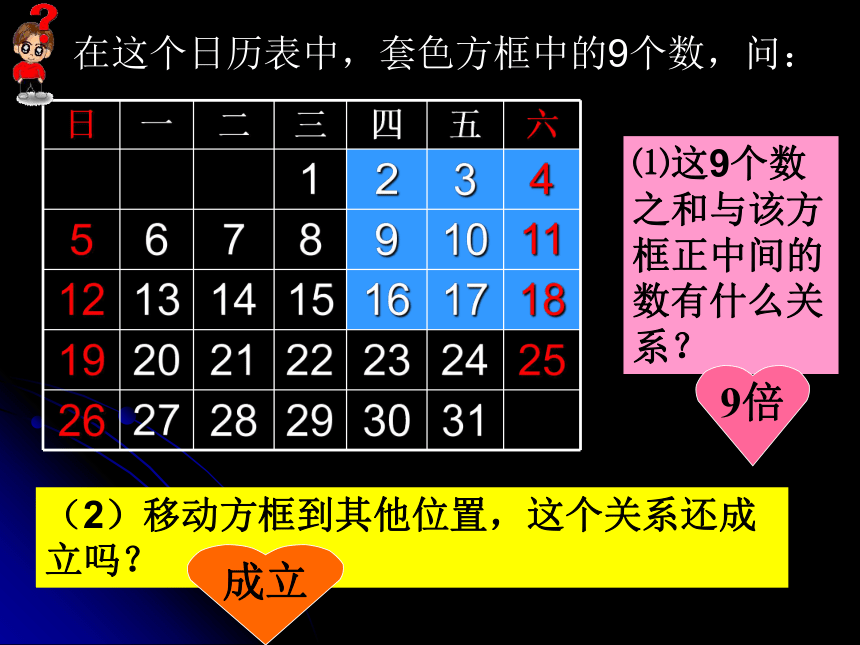
（4）从上往下、从右到左的对角线上相邻各数总是差6； 在这个日历表中，套色方框中的9个数，问：⑴这9个数之和与该方框正中间的数有什么关系？（2）移动方框到其他位置，这个关系还成立吗？9倍成立
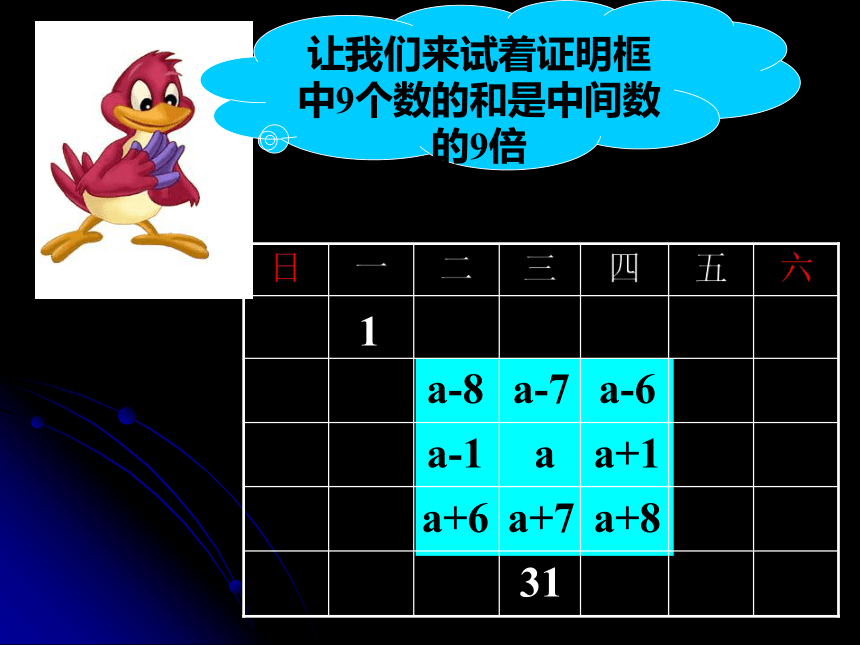
让我们来试着证明框中9个数的和是中间数的9倍aa-7a+7a-1a+1a-8a-6a+6a+8131看看两个对角线上数的和有什么关系？解：和相等！
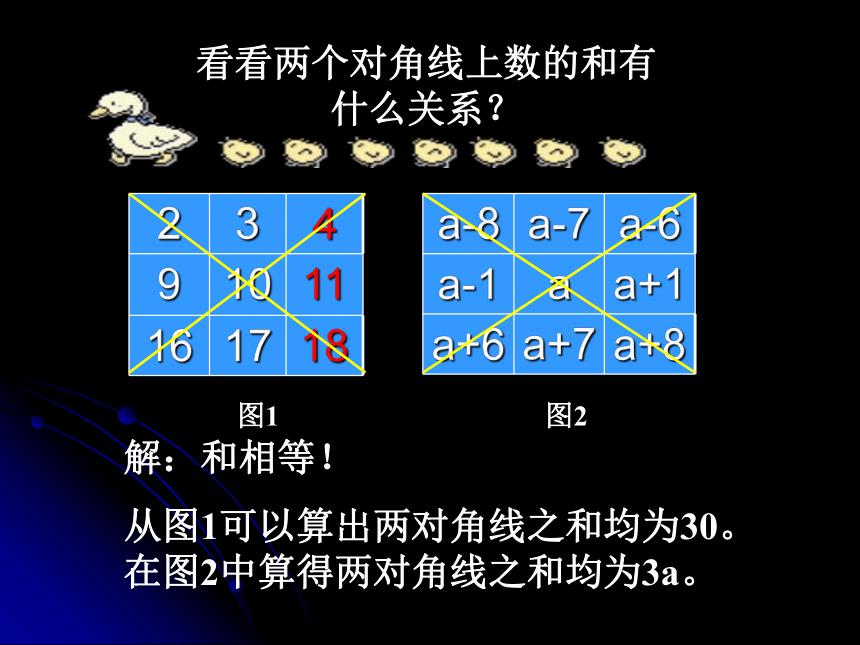
从图1可以算出两对角线之和均为30。在图2中算得两对角线之和均为3a。图1图2课后思考在2×2，4×4方框中两对角线上数字的和相等这一结论还成立吗？
请下课后自己证明！拓展练习将连续的奇数1，3，
5，7…排成如右的
数表，十字框内有5
个数，如右图：
（1）十字框内的5个数的和与框中间的数19有什么关系？这种关系对其他的圈法也成立吗?解：十字框内五个数的和为95，这种关系对其他的圈法也成立（2）若设中间的数字为a,用代数式来证明上述结论。（3）十字框框住的5个数之和能等于2000吗？能等于2008吗？能等于2015吗？若能，写出这五个数.课堂小结 ： 1本节课体现了从特殊到一般的数学思想 学会借用字母代替数来证明一般规律3 本节揭示了生活中处处存在数学4 通过探索规律，更好地发散了学生的思维练一练作业习题3.7
“问题解决”和“联系拓广”