2.2.1 直线的点斜式方程-【帮课堂】2022-2023学年高二数学《考点·题型·技巧》精讲与精练(学案+练习)(含解析)
文档属性
| 名称 | 2.2.1 直线的点斜式方程-【帮课堂】2022-2023学年高二数学《考点·题型·技巧》精讲与精练(学案+练习)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2.2直线的方程
2.2.1 直线的点斜式方程
【考点梳理】
考点一 直线的点斜式方程和斜截式方程
类别 点斜式 斜截式
适用范围 斜率存在
已知条件 点P(x0,y0)和斜率k 斜率k和在y轴上的截距b
图示 INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\L47.TIF" \* MERGEFORMAT INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\L47.TIF" \* MERGEFORMATINET INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\WORD\\L47.TIF" \* MERGEFORMATINET INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\WORD\\L47.TIF" \* MERGEFORMATINET INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\L48.TIF" \* MERGEFORMAT INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\L48.TIF" \* MERGEFORMATINET INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\WORD\\L48.TIF" \* MERGEFORMATINET INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\WORD\\L48.TIF" \* MERGEFORMATINET
方程 y-y0=k(x-x0) y=kx+b
截距 直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距
思考1 经过点P0(x0,y0)且斜率不存在的直线能否用点斜式方程来表示?
答案 不能用点斜式表示,过点P0且斜率不存在的直线为x=x0.
思考2 直线l1:y=k1x+b1,l2:y=k2x+b2平行、垂直的条件?
答案 (1)l1∥l2 k1=k2且b1≠b2,
(2)l1⊥l2 k1k2=-1.
思考3 直线在y轴上的截距是距离吗?
答案 不是,距离和截距是两个不同的概念,距离非负,而截距是一个数值.
【题型归纳】
题型一:求直线的点斜式方程
1.已知直线过,并与两坐标轴截得等腰三角形,那么直线的方程是( ).
A.或 B.或
C.或 D.或
2.已知直线的倾斜角为,且经过点,则直线的方程为( )
A. B. C. D.
3.已知点,,则经过点且经过线段AB的中点的直线方程为( )
A. B. C. D.
题型二:直线的斜截式方程
4.已知直线的倾斜角为,且在轴上的截距为,则直线的方程为( )
A. B.
C. D.
5.已知直线在x轴和y轴上的截距相等,则a的值是( )
A.或1 B.或 C. D.1
6.已知直线与直线平行,且在轴上的截距为,则的值为_________.
题型三:直线的图象的辨析
7.已知,,则直线通过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
8.直线可能是( )
A. B.
C. D.
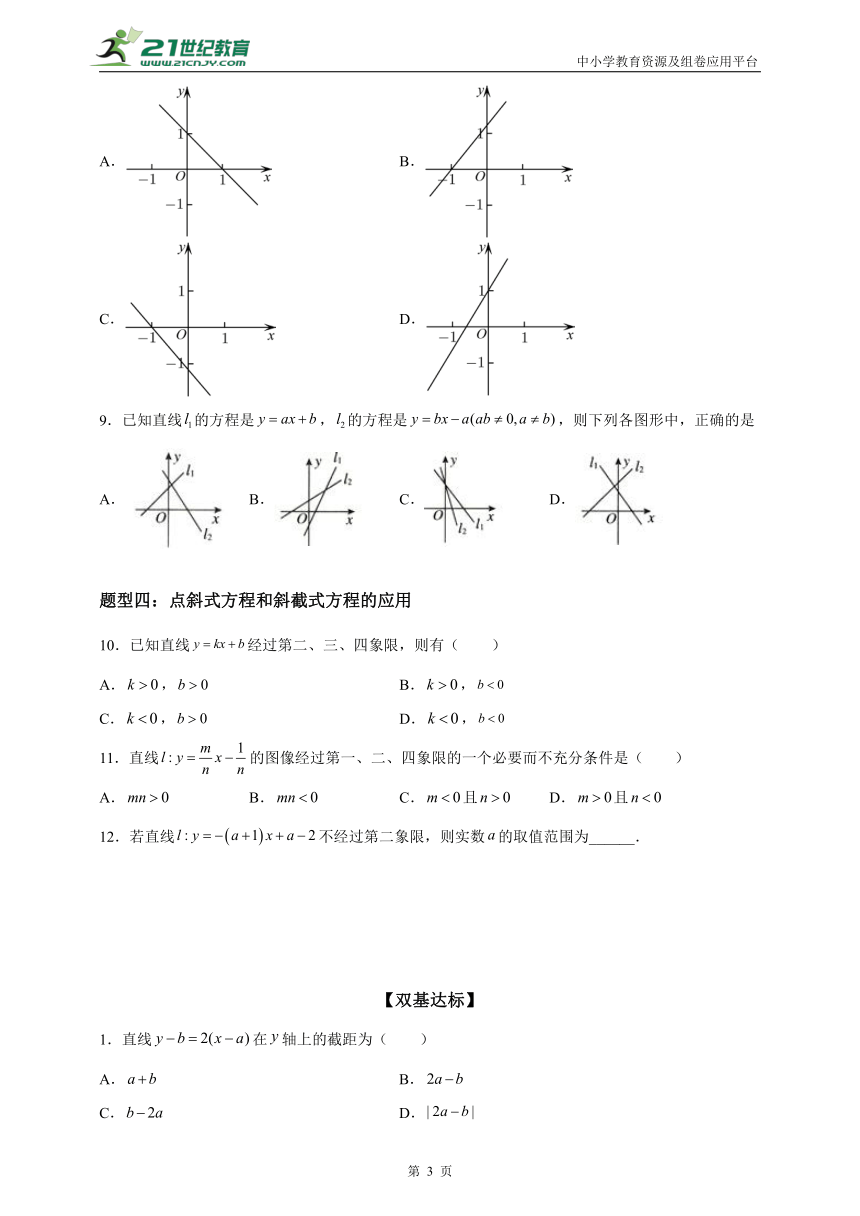
9.已知直线的方程是,的方程是,则下列各图形中,正确的是
A. B. C. D.
题型四:点斜式方程和斜截式方程的应用
10.已知直线经过第二、三、四象限,则有( )
A., B.,
C., D.,
11.直线的图像经过第一、二、四象限的一个必要而不充分条件是( )
A. B. C.且 D.且
12.若直线不经过第二象限,则实数的取值范围为______.
【双基达标】
1.直线在轴上的截距为( )
A. B.
C. D.
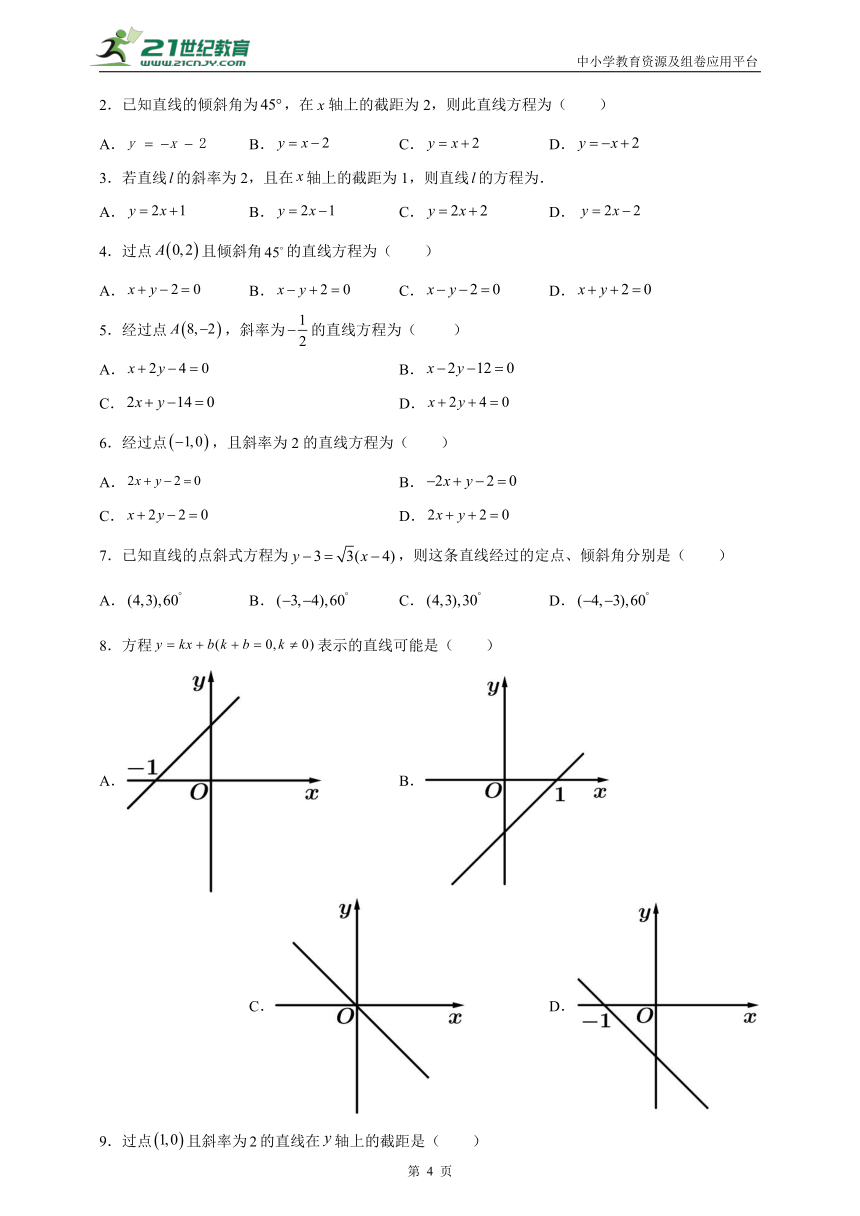
2.已知直线的倾斜角为,在x轴上的截距为2,则此直线方程为( )
A. B. C. D.
3.若直线的斜率为2,且在轴上的截距为1,则直线的方程为.
A. B. C. D.
4.过点且倾斜角的直线方程为( )
A. B. C. D.
5.经过点,斜率为的直线方程为( )
A. B.
C. D.
6.经过点,且斜率为2的直线方程为( )
A. B.
C. D.
7.已知直线的点斜式方程为,则这条直线经过的定点、倾斜角分别是( )
A. B. C. D.
8.方程表示的直线可能是( )
A. B. C. D.
9.过点且斜率为的直线在轴上的截距是( )
A. B. C. D.
10.直线恒过定点( )
A. B.
C. D.
11.过点,倾斜角为150°的直线方程为( )
A.y-2=- (x+4)
B.y-(-2)=- (x-4)
C.y-(-2)= (x-4)
D.y-2= (x+4)
12.直线l1:y=ax+b与直线l2:y=bx+a(ab≠0,a≠b)在同一平面直角坐标系内的图象只可能是( )
A. B.
C. D.
13.过点(1,3)且与原点相距为1的直线共有( ).
A.0条 B.1条 C.2条 D.3条
14.过点且与原点距离最大的直线方程是( )
A. B.
C. D.
15.直线和直线在同一坐标系中可能是( )
A. B. C. D.
16.若直线经过点,且在轴上的截距的取值范围是(3,5),则其斜率的取值范围是( )
A. B.
C. D.
17.已知,,则下列直线的方程不可能是的是( )
A. B.
C. D.
18.若与的图形有两个交点,则的取值范围是( )
A. B. C. D.或
19.已知则直线不过
A.第一象限 B.第二象限 C.第三象限 D.第四象限
20.已知过点的直线l与x轴正半轴和y轴正半轴分别交于A,B两点,当最小时,直线l的方程为( )
A. B. C. D.
21.过点且与两坐标轴围成的三角形面积为4的直线的条数为( )
A.1 B.2 C.3 D.4
22.数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称为三角形的欧拉线已知的顶点,则的欧拉线方程为( )
A. B.
C. D.
二、多选题
23.关于直线,下列说法正确的有( )
A.过点 B.斜率为
C.倾斜角为60° D.在轴上的截距为1
24.已知,,,则( )
A.直线与线段有公共点
B.直线的倾斜角大于
C.的边上的中线所在直线的方程为
D.的边上的高所在直线的方程为
25.下列说法不正确的是( )
A.直线与两坐标轴围成的三角形面积是2
B.若三条直线,,能构成三角形,则的取值范围是且
C.任意一条过点的直线方程可表示为
D.经过点且在轴和轴上截距都相等的直线方程为
26.下列说法不正确的是( )
A.不能表示过点且斜率为的直线方程;
B.在轴 轴上的截距分别为,的直线方程为;
C.直线与轴的交点到原点的距离为;
D.设,,若直线与线段有交点,则的取值范围是
三、填空题
27.已知直线L过点且倾斜角为,则l的点斜式方程为_______.
28.经过点,且以为一个方向向量的直线的方程为_____.
29.过点且到原点距离最大的直线方程为________.
30.若直线绕着其上一点逆时针旋转后得到直线,则直线的点斜式方程为_________.
31.已知点,若在坐标轴上存在一点,使直线的倾斜角为,则点的坐标为________.
32.如图,在两条互相垂直的道路l1,l2的一角,有一个电线杆,电线杆底部到道路l1的垂直距离为4米,到道路l2的垂直距离为3米,现在要过电线杆的底部靠近道路的一侧修建一条人行直道,使得人行道与两条垂直的道路围成的直角三角形的面积最小,则人行道的长度为________米.
四、解答题
33.的三个顶点是,,,求:
(1)边BC上的中线所在直线的方程;
(2)边BC上的高所在直线的方程;
(3)边BC的垂直平分线的方程.
34.已知直线l的方程为.
(1)求过点且与直线l垂直的直线方程;
(2)求直线与的交点,且求这个点到直线l的距离.
35.求倾斜角为直线的倾斜角的,且分别满足下列条件的直线方程:
(1)经过点;
(2)在轴上的截距为.
36.已知平行四边形ABCD的三个顶点的坐标为,,.
(1)求平行四边形ABCD的顶点D的坐标.
(2)求边AB的高所在直线方程.
37.直线l过点P(1,4),分别交x轴的正半轴和y轴的正半轴于A,B两点,O为坐标原点,当|OA|+|OB|最小时,求l的方程.
参考答案
【题型归纳】
参考答案:
1.C
【解析】
【分析】
根据直线与两坐标轴截得等腰三角形可得直线得斜率为1或-1,利用直线方程得点斜式即可求解.
【详解】
解:由题意可知,所求直线的倾斜角为或,即直线的斜率为1或-1,
故直线方程为或,
即或.
故选:C.
2.C
【解析】
【分析】
先求出斜率,再由直线的点斜式方程求解即可.
【详解】
由题意知:直线的斜率为,则直线的方程为.
故选:C.
3.C
【解析】
【分析】
求AB的中点坐标,根据直线所过的两点坐标求直线方程即可.
【详解】
由已知,AB中点为,又,
∴所求直线斜率为,故直线方程为,即.
故选:C.
4.C
【解析】
【分析】
首先求出直线的斜率,再根据斜截式计算可得;
【详解】
解:因为直线的倾斜角为,所以直线的斜率,
又直线在轴上的截距为,所以直线的方程为;
故选:C
5.A
【解析】
【分析】
分截距都为零和都不为零讨论即可.
【详解】
当截距都为零时,直线过原点,;
当截距不为零时,,.
综上:或.
故选:A.
6.-7
【解析】
【分析】
根据两条直线平行,得到的等量关系,根据直线在轴上的截距,可得所满足的等量关系式,联立方程组求得结果.
【详解】
解:因为直线与直线平行,
所以,
又直线在轴上的截距为,
所以,解得,所以,
所以.
故答案为:
7.C
【解析】
【分析】
将方程整理为一般式,即可根据斜率以及轴上的截距判断直线经过的象限.
【详解】
等价于,
根据题意,故直线必经过第一、三象限;
又因为,故直线必经过第三、四象限,
故直线必经过第一、三、四象限.
故选:C.
【点睛】
本题考查由直线方程的系数,确定直线经过的象限,属基础题.
8.B
【解析】
【分析】
根据直线斜率的正负值与定点即可判断结果.
【详解】
因为,所以A C错;
当时,,故B对;
故选:B
9.D
【解析】
【详解】
对于D:l1:y=ax+b,l2:y=bx-a.由l1可知a<0,b<0,对应l2也符合,
10.D
【解析】
【分析】
根据直线经过的象限判断出的符号,由此确定正确选项.
【详解】
∵直线经过二、三、四象限,
∴直线的斜率,.
故选:D
11.B
【解析】
【详解】
试题分析:直线的图像经过第一、二、四象限,则,所以,故A,C错误,D是充要条件,B是必要不充分条件.故选B.
考点:充分必要条件.
12.
【解析】
【分析】
根据直线的斜率和在轴上的截距建立不等式组求解即可.
【详解】
由直线不过第二象限需满足,
解得,
所以实数的取值范围为.
故答案为:
【双基达标】
1.C
【解析】
【分析】
将,转化为斜截式方程求解.
【详解】
由,得,
故直线在轴上的截距为.
故选:C
【点睛】
本题主要考查直线的方程形式,属于基础题.
2.B
【解析】
根据题中条件,先得出直线过点,由倾斜角得出斜率,进而可得出结果.
【详解】
因为直线的倾斜角为,在x轴上的截距为2,
所以该直线的斜率为,且该直线过点,
所以该直线的方程为.
故选:B.
【点睛】
本题主要考查求直线的方程,属于基础题型.
3.D
【解析】
【分析】
根据已知条件可求直线的点斜式方程.
【详解】
直线的点斜式方程为,故选D.
【点睛】
本题考查直线的点斜式方程,属于基础题.
4.B
【解析】
求得所求直线的斜率,利用点斜式可得出所求直线的方程.
【详解】
所求直线的斜率为,因此,所求直线的方程为,即.
故选:B.
5.A
【解析】
根据直线的点斜式方程,即可求得直线的方程.
【详解】
由题意,直线过点,且斜率为,
根据直线的点斜式方程,可得,即.
故选:A.
6.B
【解析】
直接利用直线的点斜式方程,再化成一般形式,即可得到答案.
【详解】
由直线的点斜式方程得:.
故选:B.
【点睛】
本题考查直线的点斜式方程,考查对方程形式的理解,属于基础题.
7.A
【解析】
【分析】
由直线的点斜式方程的特点可得到过的点和斜率,根据斜率求倾斜角.
【详解】
因为直线的点斜式方程为,
由直线的点斜式方程的特点可知,直线经过定点,
斜率为,即倾斜角为.
故选:A.
【点睛】
本题考查了直线方程的点斜式特点,属于基础题.
8.B
【解析】
【分析】
直接判断出直线经过点,对照四个选项,即可求解.
【详解】
因为,所以,代入直线方程,可得,即.
所以直线过点,故选:B.
9.D
【解析】
【分析】
求出直线与轴的交点坐标即可得解.
【详解】
所求直线方程为,该直线交轴于点,
因此,该直线在轴上的截距是.
故选:D.
10.B
【解析】
【分析】
由时,可得到定点坐标.
【详解】
当,即时,,直线恒过定点.
故选:B.
11.B
【解析】
【分析】
求出直线的倾斜角的正切值即为直线的斜率,又直线过点,则由求出的斜率和点的坐标写出直线的方程即可
【详解】
由直线的倾斜角为,得到直线的斜率
又直线过点
则直线的方程为
故选:B
12.D
【解析】
【分析】
根据直线的斜率和纵截距的正负进行判断.
【详解】
对B,斜率为正,在轴上的截距也为正,故不可能有斜率为负的情况.故B错.
当时, 和斜率均为正,且截距均为正.仅D选项满足.
故选:D
13.C
【解析】
【分析】
分类讨论,当斜率不存在时,验证成立;当斜率存在时,求出点斜式方程,再利用点到直线的距离公式求出斜率即可求解.
【详解】
当斜率不存在时,过点(1,3)的直线为,原点到直线的距离为1,满足题意;
当斜率存在时,设直线的斜率为,则直线方程为,
即,
则原点到直线的距离,解得,
即直线方程为,
即满足题意的直线有2条.
故选:C
【点睛】
本题考查了点斜式方程、点到直线的距离公式,考查了分类讨论的思想,属于基础题.
14.A
【解析】
【分析】
结合图形可知,所求直线为过点且与原点和点连线垂直的直线,通过点斜式即可得结果.
【详解】
结合图形可知,所求直线为过点且与原点和点连线垂直的直线,其斜率为,直线方程为,即.
故选:A.
15.D
【解析】
【分析】
由四个选项中的可知,分别由四个选项中的的符号推导的斜率和纵截距的符号可得解.
【详解】
根据题意可知,,
对于、、,由可知,,所以:的斜率为正数,故、、不正确;
对于,由可知,,此时:符合,故正确.
故选:D.
【点睛】
本题考查了根据直线方程识别图象,属于基础题.
16.A
【解析】
【分析】
先得出直线的点斜式方程,求得直线在x轴上的截距,建立不等式可得选项.
【详解】
设直线的斜率为k,则直线方程为y-2=k(x-1),
令y=0,得直线l在x轴上的截距为1-,则3<1-<5,
解得
所以直线的斜率的取值范围为.
故选:A
17.B
【解析】
【分析】
根据直线斜率与轴上的截距的关系判断选项即可得解.
【详解】
,
直线的方程在轴上的截距不小于2,且当时,轴上的截距为2,
故D正确,当时,, 故B不正确,当时,或,由图象知AC正确.
故选:B
18.A
【解析】
【分析】
根据题意,可知表示关于轴对称的两条射线,表示斜率为1,在轴上的截距为的直线,画出图形,分析判断即可求出的取值范围.
【详解】
解:表示关于轴对称的两条射线,
表示斜率为1,在轴上的截距为的直线,
根据题意,画出大致图形,如下图,
若与的图形有两个交点,且,则根据图形可知.
故选:A.
【点睛】
本题考查由两直线的交点个数从而求参数范围,考查直线的斜率和截距,以及直线的方程和图象,考查数形结合思想.
19.B
【解析】
【分析】
将直线方程整理为斜截式,结合其斜截式方程确定直线经过的象限即可.
【详解】
直线方程即:,
其斜率,直线在轴的截距,
据此可知直线不经过第二象限.
本题选择B选项.
【点睛】
本题主要考查直线方程及其应用,属于基础题.
20.B
【解析】
【分析】
由题意结合三角函数的知识可得,,结合正弦的二倍角公式可得,求出后即可得直线的斜率,再由点斜式即可得解.
【详解】
设,如图:
则,,
所以,
所以当即时,最小,
此时,直线的倾斜角为,斜率,
所以直线l的方程为即.
故选:B.
【点睛】
本题考查了三角函数、三角恒等变换的应用,考查了直线方程的求解,关键是合理转化条件,属于中档题.
21.C
【解析】
【分析】
设直线的斜率为,得到,分别求得直线在坐标轴上的截距,根据题意列出方程,即,分类讨论,即可求解.
【详解】
由题意知,所求直线的斜率一定存在,设直线的斜率为,
则直线方程为,即,
令,可得;令,可得,
因为过点且与两坐标轴围成的三角形面积为4,
可得,整理得,
当时,可得,解得;
当时,可得,解得或,
所以满足条件的直线方程共有3条.
故选:C.
22.D
【解析】
【分析】
根据题意得出的欧拉线即为线段的垂直平分线,然后求出线段的垂直平分线的方程即可.
【详解】
因为,所以线段的中点的坐标,线段所在直线的斜率,则线段的垂直平分线的方程为,即,因为,所以的外心、重心、垂心都在线段的垂直平分线上,所以的欧拉线方程为.
故选:D
【点睛】
本题主要考走查直线的方程,解题的关键是准确找出欧拉线,属于中档题.
23.BC
【解析】
【分析】
A. 当时,,所以该选项错误;
B. 直线的斜率为,所以该选项正确;
C.直线的倾斜角为60°,所以该选项正确;
D. 当时,,所以该选项错误.
【详解】
A. 当时,,所以直线不经过点,所以该选项错误;
B. 由题得,所以直线的斜率为,所以该选项正确;
C. 由于直线的斜率为,所以直线的倾斜角为60°,所以该选项正确;
D. 当时,,所以直线在轴上的截距不为1,所以该选项错误.
故选:BC
24.BCD
【解析】
【分析】
因为,,所以可以判断A错误;因为,所以直线的倾斜角大于,B正确;因为求出直线方程可判断C、D.
【详解】
、
因为,,所以直线与线段无公共点,A错误;
因为,所以直线的倾斜角大于,B正确;
因为线段的中点为,所以边上的中线所在直线的方程为,C正确;
因为,所以上的高所在直线的方程为,即,D正确.
故选:BCD
25.BCD
【解析】
【分析】
对于选项直接求出交点即可得出面积;对于选项要分类讨论,一类是平行不可以,一类是过原点不可以;
对于选项要考虑斜率存在不存在问题;对于选项也要分类讨论,一类是直接设截距式,一类是过原点.
【详解】
对于选项,直线与两坐标轴交点为,,
直线与两坐标轴围成的三角形的面积是,故正确;
对于选项,构不成三角形时,即,与已知直线平行或者过原点,故且且,故选项错误;
对于选项,当斜率存在时,过点的直线可表示为,当斜率不存在时,.故选项错误;
对于选项,设直线的截距式为,把点代入,且,可求出直线方程为.当直线过原点的时,截距也相等,
可求出直线方程为为,故选项错误.
故选:.
26.BCD
【解析】
【分析】
A由不过即知正误;B注意截距式能表示直线的前提;C注意斜截式截距的符号;D根据直线过定点,由定点与线段上的点所成直线的斜率范围判断的范围是否正确.
【详解】
A:过点且斜率为的直线方程为,而不过,故正确;
B:当轴 轴上的截距,存在0时,不能用表示,故错误;
C:当时,与轴的交点到原点的距离为,故错误;
D:由过定点,该定点与线段上的点所成直线的斜率范围为,故要使直线与线段有交点,则,故错误.
故选:BCD
27.
【解析】
【分析】
根据直线的点斜式方程可得答案.
【详解】
由题意知直线L的斜率,所以l的点斜式方程为.
故答案为:.
【点睛】
本题考查直线的点斜式方程,属于基础题.
28.
【解析】
求出直线的斜率,可得出直线的点斜式方程,化为一般式即可.
【详解】
直线的斜率为,所以,直线的方程为,即.
故答案为:.
【点睛】
本题考查直线的方程,考查直线的方向向量与斜率的关系,考查计算能力,属于基础题.
29.
【解析】
【分析】
若设点的坐标为,则所求的直线为过点且与垂直的直线,先求出直线的斜率,则可得所求直线的斜率,然后利用点斜式可求得直线方程.
【详解】
解:设点的坐标为,则过点且到原点距离最大的直线方程为与垂直的直线,
因为,所以所求直线的斜率为,
所以所求的直线方程为,即
故答案为:
【点睛】
此题考查两直线的位置关系,直线方程的求解,属于基础题.
30.
【解析】
【分析】
先根据已知直线斜率求得倾斜角,旋转得到直线的倾斜角,再根据其斜率和定点得到点斜式方程.
【详解】
∵直线的斜率为1,∴倾斜角为45°.将其逆时针旋转90°后得到直线,
则直线的倾斜角为135°,∴直线的斜率为.
又点在直线上,∴直线的点斜式方程为.
故答案为:.
【点睛】
本题考查了直线的点斜式方程,属于基础题.
31.或
【解析】
【分析】
由直线的倾斜角求出直线的斜率,利用点斜式求得直线方程,进而得到直线在两坐标轴上的截距即可.
【详解】
∵直线PA的倾斜角为45°,∴斜率为tan45°=1,∴直线PA的方程为y-(-1)=1×(x-2),即x-y-3=0.
令y=0,得x=3;令x=0,得y=-3.∴点P的坐标是(3,0)或(0,-3).
故答案为:(3,0)或(0,-3).
【点睛】
本题考查了直线的倾斜角和斜率,考查了直线在坐标轴上的截距,属于基础题.
32.10
【解析】
建立平面直角坐标系,设出直线方程为y-4=k(x-3)(k<0),
分别写出A,B(0,4-3k),进而根据三角形面积公式求解即可
【详解】
如图建立平面直角坐标系,
设人行道所在直线方程为y-4=k(x-3)(k<0),所以A,B(0,4-3k),
所以△ABO的面积S= (4-3k)= ,因为k<0,
所以,-9k-≥2=24,当且仅当-9k=-,即k=-时取等号,此时,A(6,0),B(0,8),所以人行道的长度为10米.
【点睛】
解题关键在于,建立直角坐标系后得出A,B(0,4-3k),进而利用面积公式和均值不等式求解,难度属于基础题
33.(1);(2);(3)
【解析】
【分析】
(1)求得BC的中点坐标,结合A点坐标,求得中线方程;
(2)求得BC的斜率,从而求得其上的高的斜率,且过,求得高的方程;
(3)由(1)知BC的中点坐标,由(2)知高的斜率为,写出垂直平分线的方程;
【详解】
(1)BC的中点坐标为
则边BC上的中线所在直线的方程为;
(2)边BC的斜率为,则其上的高的斜率为,且过,
则边BC上的高所在直线的方程为;
(3)由(1)知BC的中点坐标,由(2)知高的斜率为,
则边BC的垂直平分线的方程为.
34.(1)(2)1
【解析】
【分析】
(1)与l垂直的直线方程可设为 ,再将点 代入方程可得;(2)先求两直线的交点,再用点到直线的距离公式可得点到直线l的距离.
【详解】
解:(1)设与直线垂直的直线方程为,把代入,得,解得,
∴所求直线方程为.
(2)解方程组得∴直线与的交点为,点到直线的距离.
【点睛】
本题考查两直线垂直时方程的求法和点到直线的距离公式.
35.(1);(2).
【解析】
(1)由题意可得的倾斜角为,可得所求直线倾斜角为,斜率为1,代入直线的点斜式方程,即可得答案;
(2)由题意,代入直线的斜截式方程,化简整理,即可得答案.
【详解】
由于直线的斜率为,且倾斜角,所以其倾斜角为.
由题意知所求直线的倾斜角为,所求直线的斜率.
(1)由于直线经过点,由直线的点斜式方程得,即.
(2)由于直线在轴上的截距为,由直线的斜截式方程得,即.
36.(1)
(2)
【解析】
【分析】
(1)结合中点坐标公式求得正确答案.
(2)结合点斜式求得求边AB的高所在直线方程.
(1)
的顶点,,,则对角线AC中点为.
于是得对角线BD的中点是,设,因此有,,
解得:.
所以平行四边形ABCD的顶点.
(2)
依题意,直线AB的斜率,
则边AB上的高所在直线的斜率为,于是有:,
即.
所以边AB上的高所在直线的方程为.
37.2x+y-6=0
【解析】
【分析】
根据题意可写出直线的方程为y-4=k(x-1)(k<0),求得A,B(0,4-k),进而得到|OA|+|OB|=+(4-k)=5-,再由均值不等式可得到最值.
【详解】
依题意,l的斜率存在,且斜率为负,
设直线l的斜率为k,
则直线l的方程为y-4=k(x-1)(k<0).
令y=0,可得A;
令x=0,可得,
|OA|+|OB|=+=5-
=5+≥5+4=9.
当且仅当=且k<0,
即k=-2时,|OA|+|OB|取最小值.
此时l的方程为:2x+y-6=0.
试卷第1页,共3页
2.2直线的方程
2.2.1 直线的点斜式方程
【考点梳理】
考点一 直线的点斜式方程和斜截式方程
类别 点斜式 斜截式
适用范围 斜率存在
已知条件 点P(x0,y0)和斜率k 斜率k和在y轴上的截距b
图示 INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\L47.TIF" \* MERGEFORMAT INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\L47.TIF" \* MERGEFORMATINET INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\WORD\\L47.TIF" \* MERGEFORMATINET INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\WORD\\L47.TIF" \* MERGEFORMATINET INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\L48.TIF" \* MERGEFORMAT INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\L48.TIF" \* MERGEFORMATINET INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\WORD\\L48.TIF" \* MERGEFORMATINET INCLUDEPICTURE "H:\\莫成程\\2020\\同步\\数学\\人教A版 选择性必修第一册(新教材)\\WORD\\L48.TIF" \* MERGEFORMATINET
方程 y-y0=k(x-x0) y=kx+b
截距 直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距
思考1 经过点P0(x0,y0)且斜率不存在的直线能否用点斜式方程来表示?
答案 不能用点斜式表示,过点P0且斜率不存在的直线为x=x0.
思考2 直线l1:y=k1x+b1,l2:y=k2x+b2平行、垂直的条件?
答案 (1)l1∥l2 k1=k2且b1≠b2,
(2)l1⊥l2 k1k2=-1.
思考3 直线在y轴上的截距是距离吗?
答案 不是,距离和截距是两个不同的概念,距离非负,而截距是一个数值.
【题型归纳】
题型一:求直线的点斜式方程
1.已知直线过,并与两坐标轴截得等腰三角形,那么直线的方程是( ).
A.或 B.或
C.或 D.或
2.已知直线的倾斜角为,且经过点,则直线的方程为( )
A. B. C. D.
3.已知点,,则经过点且经过线段AB的中点的直线方程为( )
A. B. C. D.
题型二:直线的斜截式方程
4.已知直线的倾斜角为,且在轴上的截距为,则直线的方程为( )
A. B.
C. D.
5.已知直线在x轴和y轴上的截距相等,则a的值是( )
A.或1 B.或 C. D.1
6.已知直线与直线平行,且在轴上的截距为,则的值为_________.
题型三:直线的图象的辨析
7.已知,,则直线通过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
8.直线可能是( )
A. B.
C. D.
9.已知直线的方程是,的方程是,则下列各图形中,正确的是
A. B. C. D.
题型四:点斜式方程和斜截式方程的应用
10.已知直线经过第二、三、四象限,则有( )
A., B.,
C., D.,
11.直线的图像经过第一、二、四象限的一个必要而不充分条件是( )
A. B. C.且 D.且
12.若直线不经过第二象限,则实数的取值范围为______.
【双基达标】
1.直线在轴上的截距为( )
A. B.
C. D.
2.已知直线的倾斜角为,在x轴上的截距为2,则此直线方程为( )
A. B. C. D.
3.若直线的斜率为2,且在轴上的截距为1,则直线的方程为.
A. B. C. D.
4.过点且倾斜角的直线方程为( )
A. B. C. D.
5.经过点,斜率为的直线方程为( )
A. B.
C. D.
6.经过点,且斜率为2的直线方程为( )
A. B.
C. D.
7.已知直线的点斜式方程为,则这条直线经过的定点、倾斜角分别是( )
A. B. C. D.
8.方程表示的直线可能是( )
A. B. C. D.
9.过点且斜率为的直线在轴上的截距是( )
A. B. C. D.
10.直线恒过定点( )
A. B.
C. D.
11.过点,倾斜角为150°的直线方程为( )
A.y-2=- (x+4)
B.y-(-2)=- (x-4)
C.y-(-2)= (x-4)
D.y-2= (x+4)
12.直线l1:y=ax+b与直线l2:y=bx+a(ab≠0,a≠b)在同一平面直角坐标系内的图象只可能是( )
A. B.
C. D.
13.过点(1,3)且与原点相距为1的直线共有( ).
A.0条 B.1条 C.2条 D.3条
14.过点且与原点距离最大的直线方程是( )
A. B.
C. D.
15.直线和直线在同一坐标系中可能是( )
A. B. C. D.
16.若直线经过点,且在轴上的截距的取值范围是(3,5),则其斜率的取值范围是( )
A. B.
C. D.
17.已知,,则下列直线的方程不可能是的是( )
A. B.
C. D.
18.若与的图形有两个交点,则的取值范围是( )
A. B. C. D.或
19.已知则直线不过
A.第一象限 B.第二象限 C.第三象限 D.第四象限
20.已知过点的直线l与x轴正半轴和y轴正半轴分别交于A,B两点,当最小时,直线l的方程为( )
A. B. C. D.
21.过点且与两坐标轴围成的三角形面积为4的直线的条数为( )
A.1 B.2 C.3 D.4
22.数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称为三角形的欧拉线已知的顶点,则的欧拉线方程为( )
A. B.
C. D.
二、多选题
23.关于直线,下列说法正确的有( )
A.过点 B.斜率为
C.倾斜角为60° D.在轴上的截距为1
24.已知,,,则( )
A.直线与线段有公共点
B.直线的倾斜角大于
C.的边上的中线所在直线的方程为
D.的边上的高所在直线的方程为
25.下列说法不正确的是( )
A.直线与两坐标轴围成的三角形面积是2
B.若三条直线,,能构成三角形,则的取值范围是且
C.任意一条过点的直线方程可表示为
D.经过点且在轴和轴上截距都相等的直线方程为
26.下列说法不正确的是( )
A.不能表示过点且斜率为的直线方程;
B.在轴 轴上的截距分别为,的直线方程为;
C.直线与轴的交点到原点的距离为;
D.设,,若直线与线段有交点,则的取值范围是
三、填空题
27.已知直线L过点且倾斜角为,则l的点斜式方程为_______.
28.经过点,且以为一个方向向量的直线的方程为_____.
29.过点且到原点距离最大的直线方程为________.
30.若直线绕着其上一点逆时针旋转后得到直线,则直线的点斜式方程为_________.
31.已知点,若在坐标轴上存在一点,使直线的倾斜角为,则点的坐标为________.
32.如图,在两条互相垂直的道路l1,l2的一角,有一个电线杆,电线杆底部到道路l1的垂直距离为4米,到道路l2的垂直距离为3米,现在要过电线杆的底部靠近道路的一侧修建一条人行直道,使得人行道与两条垂直的道路围成的直角三角形的面积最小,则人行道的长度为________米.
四、解答题
33.的三个顶点是,,,求:
(1)边BC上的中线所在直线的方程;
(2)边BC上的高所在直线的方程;
(3)边BC的垂直平分线的方程.
34.已知直线l的方程为.
(1)求过点且与直线l垂直的直线方程;
(2)求直线与的交点,且求这个点到直线l的距离.
35.求倾斜角为直线的倾斜角的,且分别满足下列条件的直线方程:
(1)经过点;
(2)在轴上的截距为.
36.已知平行四边形ABCD的三个顶点的坐标为,,.
(1)求平行四边形ABCD的顶点D的坐标.
(2)求边AB的高所在直线方程.
37.直线l过点P(1,4),分别交x轴的正半轴和y轴的正半轴于A,B两点,O为坐标原点,当|OA|+|OB|最小时,求l的方程.
参考答案
【题型归纳】
参考答案:
1.C
【解析】
【分析】
根据直线与两坐标轴截得等腰三角形可得直线得斜率为1或-1,利用直线方程得点斜式即可求解.
【详解】
解:由题意可知,所求直线的倾斜角为或,即直线的斜率为1或-1,
故直线方程为或,
即或.
故选:C.
2.C
【解析】
【分析】
先求出斜率,再由直线的点斜式方程求解即可.
【详解】
由题意知:直线的斜率为,则直线的方程为.
故选:C.
3.C
【解析】
【分析】
求AB的中点坐标,根据直线所过的两点坐标求直线方程即可.
【详解】
由已知,AB中点为,又,
∴所求直线斜率为,故直线方程为,即.
故选:C.
4.C
【解析】
【分析】
首先求出直线的斜率,再根据斜截式计算可得;
【详解】
解:因为直线的倾斜角为,所以直线的斜率,
又直线在轴上的截距为,所以直线的方程为;
故选:C
5.A
【解析】
【分析】
分截距都为零和都不为零讨论即可.
【详解】
当截距都为零时,直线过原点,;
当截距不为零时,,.
综上:或.
故选:A.
6.-7
【解析】
【分析】
根据两条直线平行,得到的等量关系,根据直线在轴上的截距,可得所满足的等量关系式,联立方程组求得结果.
【详解】
解:因为直线与直线平行,
所以,
又直线在轴上的截距为,
所以,解得,所以,
所以.
故答案为:
7.C
【解析】
【分析】
将方程整理为一般式,即可根据斜率以及轴上的截距判断直线经过的象限.
【详解】
等价于,
根据题意,故直线必经过第一、三象限;
又因为,故直线必经过第三、四象限,
故直线必经过第一、三、四象限.
故选:C.
【点睛】
本题考查由直线方程的系数,确定直线经过的象限,属基础题.
8.B
【解析】
【分析】
根据直线斜率的正负值与定点即可判断结果.
【详解】
因为,所以A C错;
当时,,故B对;
故选:B
9.D
【解析】
【详解】
对于D:l1:y=ax+b,l2:y=bx-a.由l1可知a<0,b<0,对应l2也符合,
10.D
【解析】
【分析】
根据直线经过的象限判断出的符号,由此确定正确选项.
【详解】
∵直线经过二、三、四象限,
∴直线的斜率,.
故选:D
11.B
【解析】
【详解】
试题分析:直线的图像经过第一、二、四象限,则,所以,故A,C错误,D是充要条件,B是必要不充分条件.故选B.
考点:充分必要条件.
12.
【解析】
【分析】
根据直线的斜率和在轴上的截距建立不等式组求解即可.
【详解】
由直线不过第二象限需满足,
解得,
所以实数的取值范围为.
故答案为:
【双基达标】
1.C
【解析】
【分析】
将,转化为斜截式方程求解.
【详解】
由,得,
故直线在轴上的截距为.
故选:C
【点睛】
本题主要考查直线的方程形式,属于基础题.
2.B
【解析】
根据题中条件,先得出直线过点,由倾斜角得出斜率,进而可得出结果.
【详解】
因为直线的倾斜角为,在x轴上的截距为2,
所以该直线的斜率为,且该直线过点,
所以该直线的方程为.
故选:B.
【点睛】
本题主要考查求直线的方程,属于基础题型.
3.D
【解析】
【分析】
根据已知条件可求直线的点斜式方程.
【详解】
直线的点斜式方程为,故选D.
【点睛】
本题考查直线的点斜式方程,属于基础题.
4.B
【解析】
求得所求直线的斜率,利用点斜式可得出所求直线的方程.
【详解】
所求直线的斜率为,因此,所求直线的方程为,即.
故选:B.
5.A
【解析】
根据直线的点斜式方程,即可求得直线的方程.
【详解】
由题意,直线过点,且斜率为,
根据直线的点斜式方程,可得,即.
故选:A.
6.B
【解析】
直接利用直线的点斜式方程,再化成一般形式,即可得到答案.
【详解】
由直线的点斜式方程得:.
故选:B.
【点睛】
本题考查直线的点斜式方程,考查对方程形式的理解,属于基础题.
7.A
【解析】
【分析】
由直线的点斜式方程的特点可得到过的点和斜率,根据斜率求倾斜角.
【详解】
因为直线的点斜式方程为,
由直线的点斜式方程的特点可知,直线经过定点,
斜率为,即倾斜角为.
故选:A.
【点睛】
本题考查了直线方程的点斜式特点,属于基础题.
8.B
【解析】
【分析】
直接判断出直线经过点,对照四个选项,即可求解.
【详解】
因为,所以,代入直线方程,可得,即.
所以直线过点,故选:B.
9.D
【解析】
【分析】
求出直线与轴的交点坐标即可得解.
【详解】
所求直线方程为,该直线交轴于点,
因此,该直线在轴上的截距是.
故选:D.
10.B
【解析】
【分析】
由时,可得到定点坐标.
【详解】
当,即时,,直线恒过定点.
故选:B.
11.B
【解析】
【分析】
求出直线的倾斜角的正切值即为直线的斜率,又直线过点,则由求出的斜率和点的坐标写出直线的方程即可
【详解】
由直线的倾斜角为,得到直线的斜率
又直线过点
则直线的方程为
故选:B
12.D
【解析】
【分析】
根据直线的斜率和纵截距的正负进行判断.
【详解】
对B,斜率为正,在轴上的截距也为正,故不可能有斜率为负的情况.故B错.
当时, 和斜率均为正,且截距均为正.仅D选项满足.
故选:D
13.C
【解析】
【分析】
分类讨论,当斜率不存在时,验证成立;当斜率存在时,求出点斜式方程,再利用点到直线的距离公式求出斜率即可求解.
【详解】
当斜率不存在时,过点(1,3)的直线为,原点到直线的距离为1,满足题意;
当斜率存在时,设直线的斜率为,则直线方程为,
即,
则原点到直线的距离,解得,
即直线方程为,
即满足题意的直线有2条.
故选:C
【点睛】
本题考查了点斜式方程、点到直线的距离公式,考查了分类讨论的思想,属于基础题.
14.A
【解析】
【分析】
结合图形可知,所求直线为过点且与原点和点连线垂直的直线,通过点斜式即可得结果.
【详解】
结合图形可知,所求直线为过点且与原点和点连线垂直的直线,其斜率为,直线方程为,即.
故选:A.
15.D
【解析】
【分析】
由四个选项中的可知,分别由四个选项中的的符号推导的斜率和纵截距的符号可得解.
【详解】
根据题意可知,,
对于、、,由可知,,所以:的斜率为正数,故、、不正确;
对于,由可知,,此时:符合,故正确.
故选:D.
【点睛】
本题考查了根据直线方程识别图象,属于基础题.
16.A
【解析】
【分析】
先得出直线的点斜式方程,求得直线在x轴上的截距,建立不等式可得选项.
【详解】
设直线的斜率为k,则直线方程为y-2=k(x-1),
令y=0,得直线l在x轴上的截距为1-,则3<1-<5,
解得
所以直线的斜率的取值范围为.
故选:A
17.B
【解析】
【分析】
根据直线斜率与轴上的截距的关系判断选项即可得解.
【详解】
,
直线的方程在轴上的截距不小于2,且当时,轴上的截距为2,
故D正确,当时,, 故B不正确,当时,或,由图象知AC正确.
故选:B
18.A
【解析】
【分析】
根据题意,可知表示关于轴对称的两条射线,表示斜率为1,在轴上的截距为的直线,画出图形,分析判断即可求出的取值范围.
【详解】
解:表示关于轴对称的两条射线,
表示斜率为1,在轴上的截距为的直线,
根据题意,画出大致图形,如下图,
若与的图形有两个交点,且,则根据图形可知.
故选:A.
【点睛】
本题考查由两直线的交点个数从而求参数范围,考查直线的斜率和截距,以及直线的方程和图象,考查数形结合思想.
19.B
【解析】
【分析】
将直线方程整理为斜截式,结合其斜截式方程确定直线经过的象限即可.
【详解】
直线方程即:,
其斜率,直线在轴的截距,
据此可知直线不经过第二象限.
本题选择B选项.
【点睛】
本题主要考查直线方程及其应用,属于基础题.
20.B
【解析】
【分析】
由题意结合三角函数的知识可得,,结合正弦的二倍角公式可得,求出后即可得直线的斜率,再由点斜式即可得解.
【详解】
设,如图:
则,,
所以,
所以当即时,最小,
此时,直线的倾斜角为,斜率,
所以直线l的方程为即.
故选:B.
【点睛】
本题考查了三角函数、三角恒等变换的应用,考查了直线方程的求解,关键是合理转化条件,属于中档题.
21.C
【解析】
【分析】
设直线的斜率为,得到,分别求得直线在坐标轴上的截距,根据题意列出方程,即,分类讨论,即可求解.
【详解】
由题意知,所求直线的斜率一定存在,设直线的斜率为,
则直线方程为,即,
令,可得;令,可得,
因为过点且与两坐标轴围成的三角形面积为4,
可得,整理得,
当时,可得,解得;
当时,可得,解得或,
所以满足条件的直线方程共有3条.
故选:C.
22.D
【解析】
【分析】
根据题意得出的欧拉线即为线段的垂直平分线,然后求出线段的垂直平分线的方程即可.
【详解】
因为,所以线段的中点的坐标,线段所在直线的斜率,则线段的垂直平分线的方程为,即,因为,所以的外心、重心、垂心都在线段的垂直平分线上,所以的欧拉线方程为.
故选:D
【点睛】
本题主要考走查直线的方程,解题的关键是准确找出欧拉线,属于中档题.
23.BC
【解析】
【分析】
A. 当时,,所以该选项错误;
B. 直线的斜率为,所以该选项正确;
C.直线的倾斜角为60°,所以该选项正确;
D. 当时,,所以该选项错误.
【详解】
A. 当时,,所以直线不经过点,所以该选项错误;
B. 由题得,所以直线的斜率为,所以该选项正确;
C. 由于直线的斜率为,所以直线的倾斜角为60°,所以该选项正确;
D. 当时,,所以直线在轴上的截距不为1,所以该选项错误.
故选:BC
24.BCD
【解析】
【分析】
因为,,所以可以判断A错误;因为,所以直线的倾斜角大于,B正确;因为求出直线方程可判断C、D.
【详解】
、
因为,,所以直线与线段无公共点,A错误;
因为,所以直线的倾斜角大于,B正确;
因为线段的中点为,所以边上的中线所在直线的方程为,C正确;
因为,所以上的高所在直线的方程为,即,D正确.
故选:BCD
25.BCD
【解析】
【分析】
对于选项直接求出交点即可得出面积;对于选项要分类讨论,一类是平行不可以,一类是过原点不可以;
对于选项要考虑斜率存在不存在问题;对于选项也要分类讨论,一类是直接设截距式,一类是过原点.
【详解】
对于选项,直线与两坐标轴交点为,,
直线与两坐标轴围成的三角形的面积是,故正确;
对于选项,构不成三角形时,即,与已知直线平行或者过原点,故且且,故选项错误;
对于选项,当斜率存在时,过点的直线可表示为,当斜率不存在时,.故选项错误;
对于选项,设直线的截距式为,把点代入,且,可求出直线方程为.当直线过原点的时,截距也相等,
可求出直线方程为为,故选项错误.
故选:.
26.BCD
【解析】
【分析】
A由不过即知正误;B注意截距式能表示直线的前提;C注意斜截式截距的符号;D根据直线过定点,由定点与线段上的点所成直线的斜率范围判断的范围是否正确.
【详解】
A:过点且斜率为的直线方程为,而不过,故正确;
B:当轴 轴上的截距,存在0时,不能用表示,故错误;
C:当时,与轴的交点到原点的距离为,故错误;
D:由过定点,该定点与线段上的点所成直线的斜率范围为,故要使直线与线段有交点,则,故错误.
故选:BCD
27.
【解析】
【分析】
根据直线的点斜式方程可得答案.
【详解】
由题意知直线L的斜率,所以l的点斜式方程为.
故答案为:.
【点睛】
本题考查直线的点斜式方程,属于基础题.
28.
【解析】
求出直线的斜率,可得出直线的点斜式方程,化为一般式即可.
【详解】
直线的斜率为,所以,直线的方程为,即.
故答案为:.
【点睛】
本题考查直线的方程,考查直线的方向向量与斜率的关系,考查计算能力,属于基础题.
29.
【解析】
【分析】
若设点的坐标为,则所求的直线为过点且与垂直的直线,先求出直线的斜率,则可得所求直线的斜率,然后利用点斜式可求得直线方程.
【详解】
解:设点的坐标为,则过点且到原点距离最大的直线方程为与垂直的直线,
因为,所以所求直线的斜率为,
所以所求的直线方程为,即
故答案为:
【点睛】
此题考查两直线的位置关系,直线方程的求解,属于基础题.
30.
【解析】
【分析】
先根据已知直线斜率求得倾斜角,旋转得到直线的倾斜角,再根据其斜率和定点得到点斜式方程.
【详解】
∵直线的斜率为1,∴倾斜角为45°.将其逆时针旋转90°后得到直线,
则直线的倾斜角为135°,∴直线的斜率为.
又点在直线上,∴直线的点斜式方程为.
故答案为:.
【点睛】
本题考查了直线的点斜式方程,属于基础题.
31.或
【解析】
【分析】
由直线的倾斜角求出直线的斜率,利用点斜式求得直线方程,进而得到直线在两坐标轴上的截距即可.
【详解】
∵直线PA的倾斜角为45°,∴斜率为tan45°=1,∴直线PA的方程为y-(-1)=1×(x-2),即x-y-3=0.
令y=0,得x=3;令x=0,得y=-3.∴点P的坐标是(3,0)或(0,-3).
故答案为:(3,0)或(0,-3).
【点睛】
本题考查了直线的倾斜角和斜率,考查了直线在坐标轴上的截距,属于基础题.
32.10
【解析】
建立平面直角坐标系,设出直线方程为y-4=k(x-3)(k<0),
分别写出A,B(0,4-3k),进而根据三角形面积公式求解即可
【详解】
如图建立平面直角坐标系,
设人行道所在直线方程为y-4=k(x-3)(k<0),所以A,B(0,4-3k),
所以△ABO的面积S= (4-3k)= ,因为k<0,
所以,-9k-≥2=24,当且仅当-9k=-,即k=-时取等号,此时,A(6,0),B(0,8),所以人行道的长度为10米.
【点睛】
解题关键在于,建立直角坐标系后得出A,B(0,4-3k),进而利用面积公式和均值不等式求解,难度属于基础题
33.(1);(2);(3)
【解析】
【分析】
(1)求得BC的中点坐标,结合A点坐标,求得中线方程;
(2)求得BC的斜率,从而求得其上的高的斜率,且过,求得高的方程;
(3)由(1)知BC的中点坐标,由(2)知高的斜率为,写出垂直平分线的方程;
【详解】
(1)BC的中点坐标为
则边BC上的中线所在直线的方程为;
(2)边BC的斜率为,则其上的高的斜率为,且过,
则边BC上的高所在直线的方程为;
(3)由(1)知BC的中点坐标,由(2)知高的斜率为,
则边BC的垂直平分线的方程为.
34.(1)(2)1
【解析】
【分析】
(1)与l垂直的直线方程可设为 ,再将点 代入方程可得;(2)先求两直线的交点,再用点到直线的距离公式可得点到直线l的距离.
【详解】
解:(1)设与直线垂直的直线方程为,把代入,得,解得,
∴所求直线方程为.
(2)解方程组得∴直线与的交点为,点到直线的距离.
【点睛】
本题考查两直线垂直时方程的求法和点到直线的距离公式.
35.(1);(2).
【解析】
(1)由题意可得的倾斜角为,可得所求直线倾斜角为,斜率为1,代入直线的点斜式方程,即可得答案;
(2)由题意,代入直线的斜截式方程,化简整理,即可得答案.
【详解】
由于直线的斜率为,且倾斜角,所以其倾斜角为.
由题意知所求直线的倾斜角为,所求直线的斜率.
(1)由于直线经过点,由直线的点斜式方程得,即.
(2)由于直线在轴上的截距为,由直线的斜截式方程得,即.
36.(1)
(2)
【解析】
【分析】
(1)结合中点坐标公式求得正确答案.
(2)结合点斜式求得求边AB的高所在直线方程.
(1)
的顶点,,,则对角线AC中点为.
于是得对角线BD的中点是,设,因此有,,
解得:.
所以平行四边形ABCD的顶点.
(2)
依题意,直线AB的斜率,
则边AB上的高所在直线的斜率为,于是有:,
即.
所以边AB上的高所在直线的方程为.
37.2x+y-6=0
【解析】
【分析】
根据题意可写出直线的方程为y-4=k(x-1)(k<0),求得A,B(0,4-k),进而得到|OA|+|OB|=+(4-k)=5-,再由均值不等式可得到最值.
【详解】
依题意,l的斜率存在,且斜率为负,
设直线l的斜率为k,
则直线l的方程为y-4=k(x-1)(k<0).
令y=0,可得A;
令x=0,可得,
|OA|+|OB|=+=5-
=5+≥5+4=9.
当且仅当=且k<0,
即k=-2时,|OA|+|OB|取最小值.
此时l的方程为:2x+y-6=0.
试卷第1页,共3页
