人教版数学七年级上册 1.2.3 相反数 教案
文档属性
| 名称 | 人教版数学七年级上册 1.2.3 相反数 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-17 20:23:10 | ||
图片预览



文档简介
第一章 有理数
1.2 有理数
1.2.3 相反数
一、教学目标
【知识与技能】
1.借助数轴了解相反数的概念,知道两个互为相反数的位置关系.
2.给出一个数,能求出它的相反数.
【过程与方法】
借助数轴,通过观察特例,总结出相反数的概念.从数和形两个侧面理解相反数.
【情感态度与价值观】
鼓励学生积极进行归纳、比较交流等活动.
二、课型
新授课
三、课时
第1课时
四、教学重难点
【教学重点】
理解相反数的意义,会求一个数的相反数.
【教学难点】
1.理解和掌握双重符合的简化.
2. 归纳相反数在数轴上表示的点的特征.
五、课前准备
教师:课件、三角尺、屋顶架结构图等。
学生:三角尺、铅垂纸、小刀。
六、教学过程
(一)导入新课
成语故事“南辕北辙”讲了一个人……
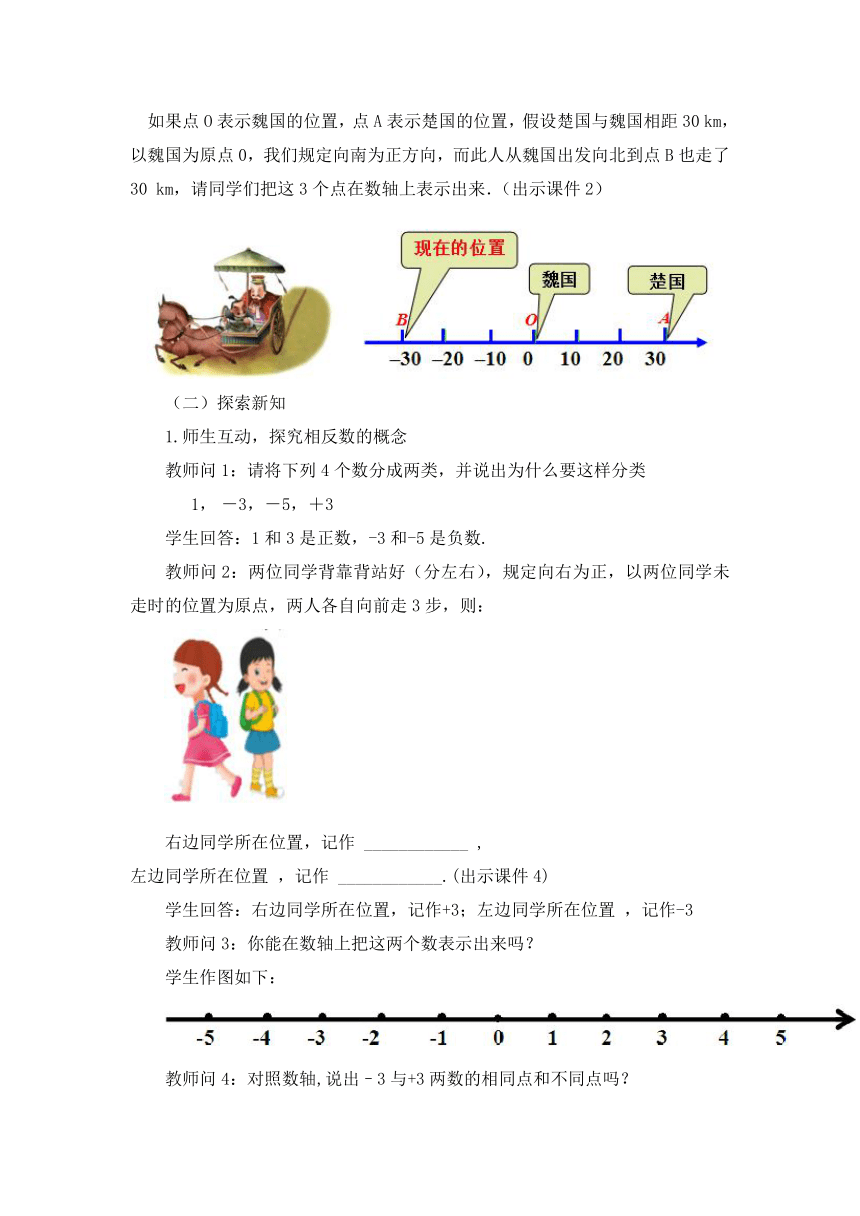
如果点O表示魏国的位置,点A表示楚国的位置,假设楚国与魏国相距30 km,以魏国为原点0,我们规定向南为正方向,而此人从魏国出发向北到点B也走了30 km,请同学们把这3个点在数轴上表示出来.(出示课件2)
(二)探索新知
1.师生互动,探究相反数的概念
教师问1:请将下列4个数分成两类,并说出为什么要这样分类
-3,-5,+3
学生回答:1和3是正数,-3和-5是负数.
教师问2:两位同学背靠背站好(分左右),规定向右为正,以两位同学未走时的位置为原点,两人各自向前走3步,则:
右边同学所在位置,记作 ____________ ,
左边同学所在位置 ,记作 ____________.(出示课件4)
学生回答:右边同学所在位置,记作+3;左边同学所在位置 ,记作-3
教师问3:你能在数轴上把这两个数表示出来吗?
学生作图如下:
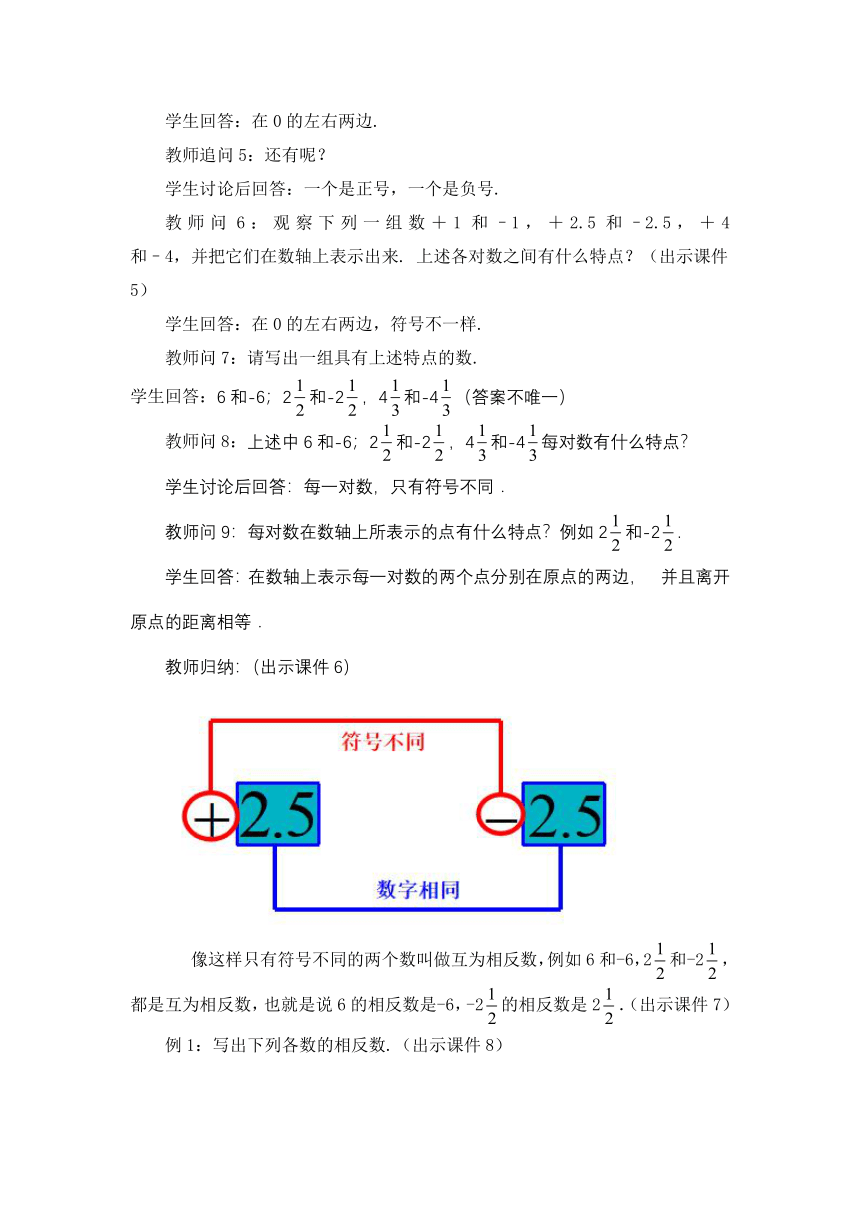
教师问4:对照数轴,说出–3与+3两数的相同点和不同点吗?
学生回答:在0的左右两边.
教师追问5:还有呢?
学生讨论后回答:一个是正号,一个是负号.
教师问6:观察下列一组数+1和–1,+2.5和–2.5,+4 和–4,并把它们在数轴上表示出来. 上述各对数之间有什么特点?(出示课件5)
学生回答:在0的左右两边,符号不一样.
教师问7:请写出一组具有上述特点的数.
学生回答:6和-6;2和-2,4和-4(答案不唯一)
教师问8:上述中6和-6;2和-2,4和-4每对数有什么特点?
学生讨论后回答:每一对数,只有符号不同.
教师问9:每对数在数轴上所表示的点有什么特点?例如2和-2.
学生回答:在数轴上表示每一对数的两个点分别在原点的两边,并且离开原点的距离相等.
教师归纳:(出示课件6)
像这样只有符号不同的两个数叫做互为相反数,例如6和-6,2和-2,都是互为相反数,也就是说6的相反数是-6,-2的相反数是2.(出示课件7)
例1:写出下列各数的相反数.(出示课件8)
9, -0.3, -2, .
师生共同解答如下:
9的相反数是-9,-03的相反数是0.3,-2的相反数是2,的相反数是-.
2.师生互动,探究相反数的几何意义
教师问10:在数轴上,画出几组表示相反数的点,并观察这两个点具有怎样的特征.如下图:(出示课件11)
学生讨论后回答:位于原点两侧,且与原点的距离相等.
教师问11:看下边的数轴,点D和点B分别位于原点的两边,且与原点的距离相等,它们分别表示什么数?
学生回答:-3和3.
教师问12:数轴上与原点的距离是2的点有几个?这些点表示的数是什么?与原点的距离是5的点呢?(出示课件12)
学生回答:数轴上与原点的距离是2的点有2个,分别是2和-2,数轴上与原点的距离是5的点有2个,分别是5和-5.
教师归纳:一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示-a和a,那么称这两个点关于原点对称,如下图:
教师问13:零的相反数是什么?为什么?
学生回答:0的相反数是0,因为到原点距离为0的数只有0.
教师问14:你怎样理解相反数定义中的“只有符号不同”和“互为”一词的含义?学生回答:“只有符号不同”说明出符号外其余的都相同,“互为”说明是对两个数说的,相反数是一对数,不能是但个数,也不能是多个数.
总结点拨:(出示课件7)
一般地,a和–a互为相反数.特别地,0的相反数是0,这里,a表示任意一个数,可以是正数、负数,也可以是0.
注意:(出示课件13)
1. 互为相反数的两个数分别位于原点的两侧;
2. 互为相反数的两个数到原点的距离相等.
3. 一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点的左右,表示a和–a,我们说这两点关于原点对称.
例2:分别写出2, , ,–2.5的相反数,并在数轴上标出各数及它们的相反数,说明各对数在数轴上的位置特点.(出示课件14)
师生共同解答如下:
分析:在所求数的前面添上“–”号,即得原数的相反数→在数轴上表示出各数→观察各对数在数轴上的位置→结论.
(出示课件15)
解:2的相反数是-2; 的相反数是 ;的相反数是-;–2.5的相反数是2.5.把这些数及它们的相反数表示在数轴上为
2和–2, 和 ,和 - ,–2.5和2.5,各对数在数轴上分别位于原点两侧,且到原点的距离相等,即在数轴上表示每对数的点都关于原点对称.
总结点拨:(出示课件16)
求相反数的方法
1. 在原数的前面加“–”号后,再进行符号化简.
2. 复杂的数在求相反数前,可先进行符号化简,然后再变号.
3.师生互动,探究多重符号的化简
教师问15:a的相反数是什么?(出示课件18)
学生回答:a的相反数是–a , a可表示任意有理数.
教师问16:如何求一个数的相反数?
学生回答:在这个数前加一个“–”号.
教师问17:若把a分别换成+5,–7,0时,这些数的相反数怎样表示?(出示课件19)
学生回答:a = +5, – a = –(+5)
a = –7, – a = –(–7)
a = 0, – a = 0
教师问18:–(+1.1)表示什么?–(–7)呢?–(–9.8)呢?
学生回答:–(+1.1)表示-1.1,–(–7) 表示7,–(–9.8) 表示9.8.
教师问19:-(+5)和-(-5)分别表示什么意思?你能化简它们吗?
学生回答:分别表示+5和-5的相反数是-5和+5
总结点拨:(出示课件20)
1.在一个数前面加上“–”号表示求这个数的相反数.
2.若a与b互为相反数,则a+b=0(或a=-b);反之,若a+b=0(或a=-b),则a与b互为相反数.
教师问20:如果在一个数前面加上“+”号所得到的结果是什么呢?
学生回答:这个数本身.
例3:化简下列各数(先读后写).(出示课件21)
(1)-(+10) (2)+(–0.15) (3)+(+3)
(4)-(-12) (5)+[-(-1.1)] (6)-[+(-7)]
师生共同解答如下:
分析:由内向外依次去括号.
解:(1) -(+10)=-10;(2) +(-0.15)=-0.15;(3)+(+3)=3;(4) -(-12)=12;
(5)+[-(-1.1)]=+(+1.1)=1.1;(6) -[+(-7)]=-(-7)=7.
总结点拨:(出示课件22)
“一查二定”
1. 式子中含偶数个“–”号时,结果正;
含奇数个“–”号时,结果为负.
2. 凡是“+”都去掉.
(三)课堂练习(出示课件24-28)
1. –8的相反数是( )
A.–8 B. C.8 D.
2.下列几对数中互为相反数的一对为( )
A.+(–8)和 –(+8) B.–(+8)与+(–8)
C.–(–8)与–(+8) D.+(+8)和-(-8)
3. 点A在数轴上的位置如图所示,则点A表示的数的相反数是_________.
4. –1.6是____的相反数,____的相反数是0.3.
5. 5的相反数是____;a的相反数是____;
6.若a= –13,则–a=____;若–a= –6,则a=____.
7.若a是负数,则–a是_____数;若–a是负数,则 a是_____数.
8. 的相反数是_____,–3x的相反数是_____.
9. (1)若a=3.2,则–a=____________ ;
(2)若–a= 2,则a=_______________;
(3)若–(–a)=3,则–a=_________;
(4) –(a–b)=____________________ .
10. 若2x+1是–9的相反数,求x的值.
11. 已知两个有理数x、y,且x+y=0, 那么这两个有理数有什么关系?
参考答案:
1.C
2.C
3.-2
4.1.6,-0.3
5.-5,-a
6.13,6
7.正,正
8. ,3x
9.(1)-3.2,(2)-2,(3)-3,(4)b-a
10. 解:由相反数的意义,得
2x+1=9
2x=8
x=4
11. 解:这两个有理数互为相反数.
(四)课堂小结
今天我们学了哪些内容:
1.相反数
(1)只有符号不同的两个数.
(2)a的相反数是-a,0的相反数是0.
(3)互为相反数的两个数和为0.
2.多重符号的化简
(1)偶数个“-”号,结果为正数.
(2)奇数个“-”号,结果为负数.
(五)课前预习
预习下节课(1.2.4)的相关内容。
知道绝对值的定义和会求一个数的绝对值
七、课后作业
1、教材10页练习1,2,3,4
2、如图,图中数轴(缺原点)的单位长度为1,点A、B表示的两数互为相反数,则点C所表示的数为( )
A.2 B.-4 C.-1 D.0
八、板书设计:
通过本课时的学习,需要我们掌握:
九、教学反思:
1.相反数的概念使有理数的各个运算法则容易表述,也揭示了两个特殊数的特征.这两个特殊数在数量上具有相同的绝对值,它们的和为零,在数轴上表示时,离开原点的距离相等等性质均有广泛的应用.所以本教学设计围绕数量和几何意义展开,渗透数形结合的思想.
2.教学引人以开放式的问题人手,培养学生的分类和发散思维的能力;把数在数轴上表示出来并观察它们的特征,在复习数轴知识的同时,渗透了数形结合的数学方法,数与形的相互转化也能加深对相反数概念的理解;问题2能帮助学生准确把握相反数的概念;问题3实际上给出了求一个数的相反数的方法.
3.本教学设计体现了新课标的教学理念,学生在教师的引导下进行自主学习,自主探究,观察归纳,重视学生的思维过程,并给学生留有发挥的余地.
1.2 有理数
1.2.3 相反数
一、教学目标
【知识与技能】
1.借助数轴了解相反数的概念,知道两个互为相反数的位置关系.
2.给出一个数,能求出它的相反数.
【过程与方法】
借助数轴,通过观察特例,总结出相反数的概念.从数和形两个侧面理解相反数.
【情感态度与价值观】
鼓励学生积极进行归纳、比较交流等活动.
二、课型
新授课
三、课时
第1课时
四、教学重难点
【教学重点】
理解相反数的意义,会求一个数的相反数.
【教学难点】
1.理解和掌握双重符合的简化.
2. 归纳相反数在数轴上表示的点的特征.
五、课前准备
教师:课件、三角尺、屋顶架结构图等。
学生:三角尺、铅垂纸、小刀。
六、教学过程
(一)导入新课
成语故事“南辕北辙”讲了一个人……
如果点O表示魏国的位置,点A表示楚国的位置,假设楚国与魏国相距30 km,以魏国为原点0,我们规定向南为正方向,而此人从魏国出发向北到点B也走了30 km,请同学们把这3个点在数轴上表示出来.(出示课件2)
(二)探索新知
1.师生互动,探究相反数的概念
教师问1:请将下列4个数分成两类,并说出为什么要这样分类
-3,-5,+3
学生回答:1和3是正数,-3和-5是负数.
教师问2:两位同学背靠背站好(分左右),规定向右为正,以两位同学未走时的位置为原点,两人各自向前走3步,则:
右边同学所在位置,记作 ____________ ,
左边同学所在位置 ,记作 ____________.(出示课件4)
学生回答:右边同学所在位置,记作+3;左边同学所在位置 ,记作-3
教师问3:你能在数轴上把这两个数表示出来吗?
学生作图如下:
教师问4:对照数轴,说出–3与+3两数的相同点和不同点吗?
学生回答:在0的左右两边.
教师追问5:还有呢?
学生讨论后回答:一个是正号,一个是负号.
教师问6:观察下列一组数+1和–1,+2.5和–2.5,+4 和–4,并把它们在数轴上表示出来. 上述各对数之间有什么特点?(出示课件5)
学生回答:在0的左右两边,符号不一样.
教师问7:请写出一组具有上述特点的数.
学生回答:6和-6;2和-2,4和-4(答案不唯一)
教师问8:上述中6和-6;2和-2,4和-4每对数有什么特点?
学生讨论后回答:每一对数,只有符号不同.
教师问9:每对数在数轴上所表示的点有什么特点?例如2和-2.
学生回答:在数轴上表示每一对数的两个点分别在原点的两边,并且离开原点的距离相等.
教师归纳:(出示课件6)
像这样只有符号不同的两个数叫做互为相反数,例如6和-6,2和-2,都是互为相反数,也就是说6的相反数是-6,-2的相反数是2.(出示课件7)
例1:写出下列各数的相反数.(出示课件8)
9, -0.3, -2, .
师生共同解答如下:
9的相反数是-9,-03的相反数是0.3,-2的相反数是2,的相反数是-.
2.师生互动,探究相反数的几何意义
教师问10:在数轴上,画出几组表示相反数的点,并观察这两个点具有怎样的特征.如下图:(出示课件11)
学生讨论后回答:位于原点两侧,且与原点的距离相等.
教师问11:看下边的数轴,点D和点B分别位于原点的两边,且与原点的距离相等,它们分别表示什么数?
学生回答:-3和3.
教师问12:数轴上与原点的距离是2的点有几个?这些点表示的数是什么?与原点的距离是5的点呢?(出示课件12)
学生回答:数轴上与原点的距离是2的点有2个,分别是2和-2,数轴上与原点的距离是5的点有2个,分别是5和-5.
教师归纳:一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示-a和a,那么称这两个点关于原点对称,如下图:
教师问13:零的相反数是什么?为什么?
学生回答:0的相反数是0,因为到原点距离为0的数只有0.
教师问14:你怎样理解相反数定义中的“只有符号不同”和“互为”一词的含义?学生回答:“只有符号不同”说明出符号外其余的都相同,“互为”说明是对两个数说的,相反数是一对数,不能是但个数,也不能是多个数.
总结点拨:(出示课件7)
一般地,a和–a互为相反数.特别地,0的相反数是0,这里,a表示任意一个数,可以是正数、负数,也可以是0.
注意:(出示课件13)
1. 互为相反数的两个数分别位于原点的两侧;
2. 互为相反数的两个数到原点的距离相等.
3. 一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点的左右,表示a和–a,我们说这两点关于原点对称.
例2:分别写出2, , ,–2.5的相反数,并在数轴上标出各数及它们的相反数,说明各对数在数轴上的位置特点.(出示课件14)
师生共同解答如下:
分析:在所求数的前面添上“–”号,即得原数的相反数→在数轴上表示出各数→观察各对数在数轴上的位置→结论.
(出示课件15)
解:2的相反数是-2; 的相反数是 ;的相反数是-;–2.5的相反数是2.5.把这些数及它们的相反数表示在数轴上为
2和–2, 和 ,和 - ,–2.5和2.5,各对数在数轴上分别位于原点两侧,且到原点的距离相等,即在数轴上表示每对数的点都关于原点对称.
总结点拨:(出示课件16)
求相反数的方法
1. 在原数的前面加“–”号后,再进行符号化简.
2. 复杂的数在求相反数前,可先进行符号化简,然后再变号.
3.师生互动,探究多重符号的化简
教师问15:a的相反数是什么?(出示课件18)
学生回答:a的相反数是–a , a可表示任意有理数.
教师问16:如何求一个数的相反数?
学生回答:在这个数前加一个“–”号.
教师问17:若把a分别换成+5,–7,0时,这些数的相反数怎样表示?(出示课件19)
学生回答:a = +5, – a = –(+5)
a = –7, – a = –(–7)
a = 0, – a = 0
教师问18:–(+1.1)表示什么?–(–7)呢?–(–9.8)呢?
学生回答:–(+1.1)表示-1.1,–(–7) 表示7,–(–9.8) 表示9.8.
教师问19:-(+5)和-(-5)分别表示什么意思?你能化简它们吗?
学生回答:分别表示+5和-5的相反数是-5和+5
总结点拨:(出示课件20)
1.在一个数前面加上“–”号表示求这个数的相反数.
2.若a与b互为相反数,则a+b=0(或a=-b);反之,若a+b=0(或a=-b),则a与b互为相反数.
教师问20:如果在一个数前面加上“+”号所得到的结果是什么呢?
学生回答:这个数本身.
例3:化简下列各数(先读后写).(出示课件21)
(1)-(+10) (2)+(–0.15) (3)+(+3)
(4)-(-12) (5)+[-(-1.1)] (6)-[+(-7)]
师生共同解答如下:
分析:由内向外依次去括号.
解:(1) -(+10)=-10;(2) +(-0.15)=-0.15;(3)+(+3)=3;(4) -(-12)=12;
(5)+[-(-1.1)]=+(+1.1)=1.1;(6) -[+(-7)]=-(-7)=7.
总结点拨:(出示课件22)
“一查二定”
1. 式子中含偶数个“–”号时,结果正;
含奇数个“–”号时,结果为负.
2. 凡是“+”都去掉.
(三)课堂练习(出示课件24-28)
1. –8的相反数是( )
A.–8 B. C.8 D.
2.下列几对数中互为相反数的一对为( )
A.+(–8)和 –(+8) B.–(+8)与+(–8)
C.–(–8)与–(+8) D.+(+8)和-(-8)
3. 点A在数轴上的位置如图所示,则点A表示的数的相反数是_________.
4. –1.6是____的相反数,____的相反数是0.3.
5. 5的相反数是____;a的相反数是____;
6.若a= –13,则–a=____;若–a= –6,则a=____.
7.若a是负数,则–a是_____数;若–a是负数,则 a是_____数.
8. 的相反数是_____,–3x的相反数是_____.
9. (1)若a=3.2,则–a=____________ ;
(2)若–a= 2,则a=_______________;
(3)若–(–a)=3,则–a=_________;
(4) –(a–b)=____________________ .
10. 若2x+1是–9的相反数,求x的值.
11. 已知两个有理数x、y,且x+y=0, 那么这两个有理数有什么关系?
参考答案:
1.C
2.C
3.-2
4.1.6,-0.3
5.-5,-a
6.13,6
7.正,正
8. ,3x
9.(1)-3.2,(2)-2,(3)-3,(4)b-a
10. 解:由相反数的意义,得
2x+1=9
2x=8
x=4
11. 解:这两个有理数互为相反数.
(四)课堂小结
今天我们学了哪些内容:
1.相反数
(1)只有符号不同的两个数.
(2)a的相反数是-a,0的相反数是0.
(3)互为相反数的两个数和为0.
2.多重符号的化简
(1)偶数个“-”号,结果为正数.
(2)奇数个“-”号,结果为负数.
(五)课前预习
预习下节课(1.2.4)的相关内容。
知道绝对值的定义和会求一个数的绝对值
七、课后作业
1、教材10页练习1,2,3,4
2、如图,图中数轴(缺原点)的单位长度为1,点A、B表示的两数互为相反数,则点C所表示的数为( )
A.2 B.-4 C.-1 D.0
八、板书设计:
通过本课时的学习,需要我们掌握:
九、教学反思:
1.相反数的概念使有理数的各个运算法则容易表述,也揭示了两个特殊数的特征.这两个特殊数在数量上具有相同的绝对值,它们的和为零,在数轴上表示时,离开原点的距离相等等性质均有广泛的应用.所以本教学设计围绕数量和几何意义展开,渗透数形结合的思想.
2.教学引人以开放式的问题人手,培养学生的分类和发散思维的能力;把数在数轴上表示出来并观察它们的特征,在复习数轴知识的同时,渗透了数形结合的数学方法,数与形的相互转化也能加深对相反数概念的理解;问题2能帮助学生准确把握相反数的概念;问题3实际上给出了求一个数的相反数的方法.
3.本教学设计体现了新课标的教学理念,学生在教师的引导下进行自主学习,自主探究,观察归纳,重视学生的思维过程,并给学生留有发挥的余地.
