探索规律(2)[上学期]

课件14张PPT。《数学》(七年级 上册)探索规律(2)第三章 字母表示数6探索规律的方法(初步) 对于与自然数n有关的探索规律的题，
可从具体的、简单的对应情境入手，
寻找所得“结果数”与n(个、次)的同一变化关系式 。
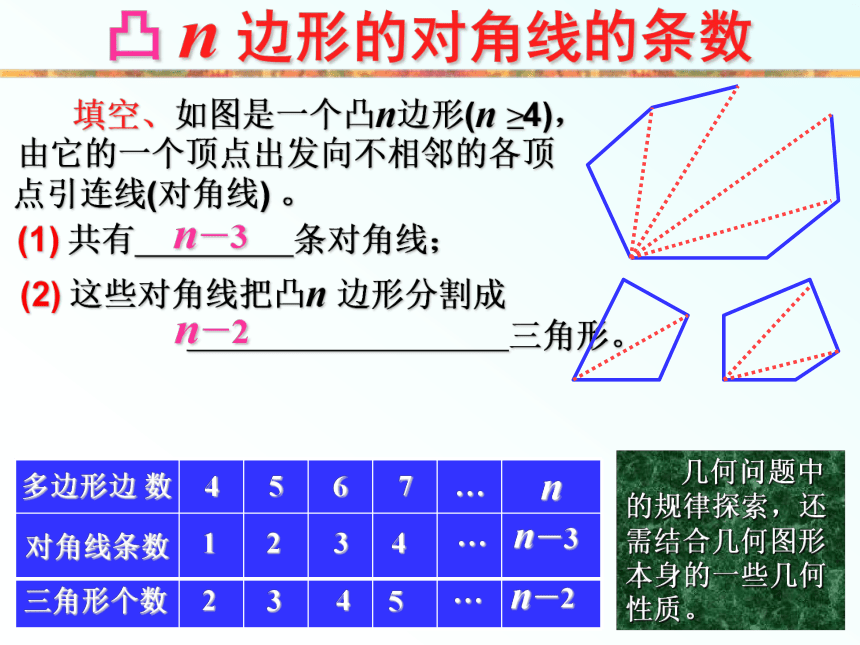
常用 列表的方法分析探索.(由特殊到一般)凸 n 边形的对角线的条数填空、如图是一个凸n边形(n ≥4)， 由它的一个顶点出发向不相邻的各顶点引连线(对角线) 。n－31234…n－32345…n－2n－2 几何问题中的规律探索，还需结合几何图形本身的一些几何性质。棱柱的面数、顶点数、棱数 填空:
(1)五棱柱共有 条棱， 个面， 个顶点;
(2)某棱柱有12个面，那么这个棱柱是 棱柱;
(3)某棱柱有30条棱，那么这个棱柱是 棱柱;
(4)某棱柱有2n个顶点，那么这个棱柱有 条棱，
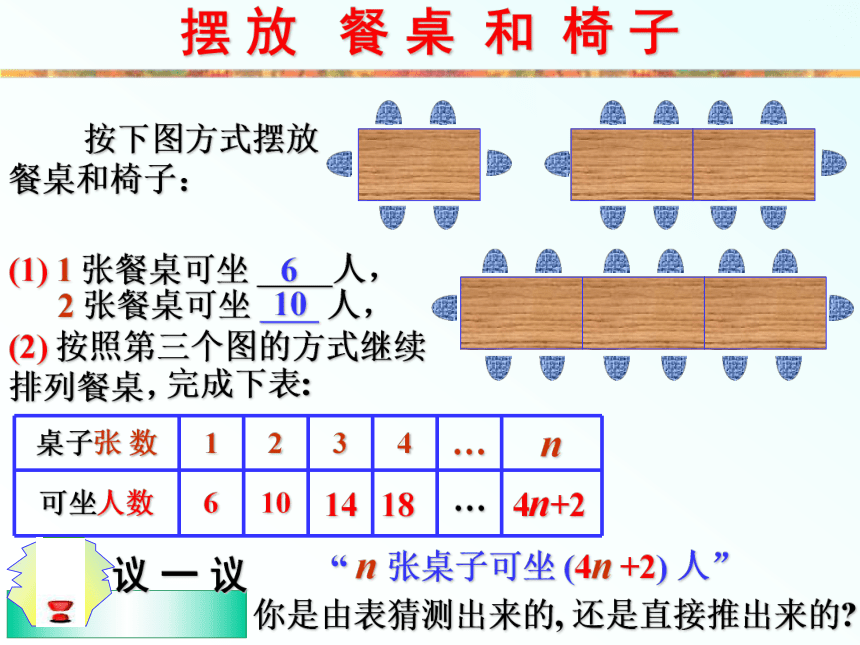
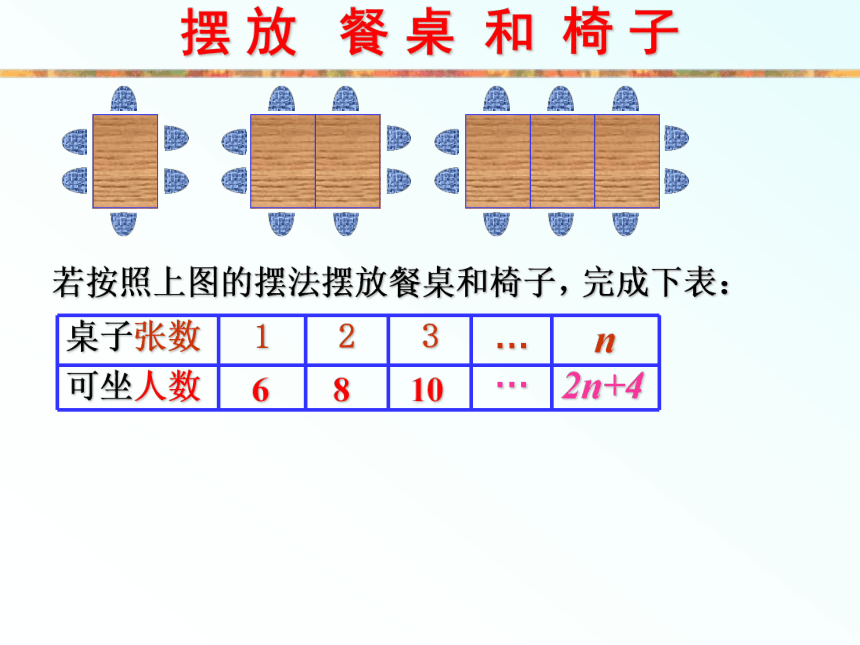
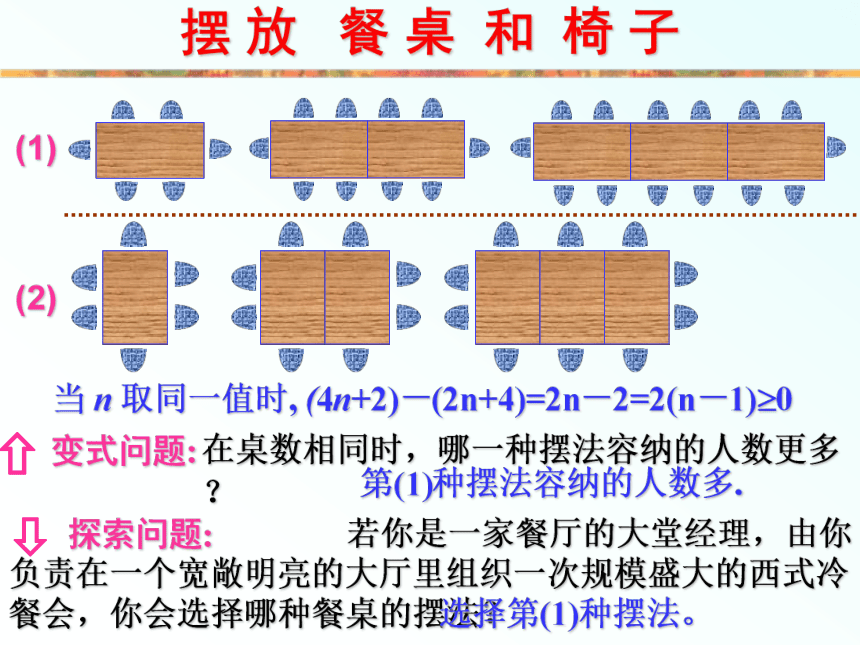
个面。157101010nn+22n3nn+2? 练一练 ?摆 放 餐 桌 和 椅 子 按下图方式摆放餐桌和椅子：(1) 1 张餐桌可坐 人， 102 张餐桌可坐 人，6(2) 按照第三个图的方式继续排列餐桌，完成下表:14184n+2…你是由表猜测出来的, 还是直接推出来的?摆 放 餐 桌 和 椅 子若按照上图的摆法摆放餐桌和椅子，完成下表：6810…2n+4摆 放 餐 桌 和 椅 子(1)
(2)当 n 取同一值时, (4n+2)－(2n+4)=2n－2=2(n－1)?0第(1)种摆法容纳的人数多.选择第(1)种摆法。辅 助 练 习 1、按规律填空，并用字母表示一般规律：
① 2，4，6， ，10，12，…
② 1，3，5， ，9，11，?
③ 2，4，8， ，32，64，…
④ 1，3，7， ，31，63… 说明? “用字母表示一般规律 ”
即“用含有 n 的式子表示第n个数”；
并且，当 n 分别用 1、2、3、4、 …代替时所求出的值
恰好分别等于这串数的第1、第2、第3、第4……个数。2n2n－12n2n － 1871615动一动：13715……?随堂练习：课本P111页　　　　随堂练习第1题对折6次后，折痕数为＿＿条；对折10次后，折痕数为＿＿＿条；对折n次后，折痕数为＿＿＿条。6310232n－1拓 展 练 习2、观察下列等式:
1=1；
l+3=4=22；
1+3+5=9=32；
1+3+5+7=16=42；
l+3+5+7+9=25=52；
(1)预测：l+3+5+7+9+11+13+15+17+19的结果;
(2)预测：l+3+5+…+(2n－1) 的结果;
(3)预测：1+3+5+…+(2n +1) 的结果·102n2( n + 1 )2拓 展 练 习 3、一串分数排列如下:
(1) 第10个分数是多少?
(2) 第2003个分数是多少?
(3) 第n个分数是多少?书上练习：P111 P113 做一做
p114 习题3.8—1；我们这节学到了什么？ 请同学们回顾本节课学习了哪些知识.
获得了哪些有指导意义的结论?1、凸 n 边形的对角线的条数；
棱柱的面数、顶点数、棱数；
摆 放 餐 桌 和 椅 子；
由偶数、奇数、平方数等
组成的一串数的规律；2、在探索规律中遇到挫折，你会怎么办？3、对自己本节课的学习情况进行评价。
（包括所学习到的探索规律的一般方法；
探索规律过程中哪些量是重要的；
探索规律的一般过程等）发现规律的途径与注意事项： ① 通过观察、分析、猜想等活动发现规律，使得问题正确解答;
② 发现的规律要经过检验，是否正确，可以避免出现错误。 说明：探索规律的过程：
问题——猜想——验证——总结——结论。如果验证不合理则进行重新探索。如果验证合理，则上升到总结并得出结论。作 业课本 p117 7 (3) (4)；
p118 (C组)—1(1)(2)(4) 2.
作业 做在书本上练习册； 64~66页