北师大版数学八年级上册第六章 数据的分析单元复习课 课件(共27张PPT)
文档属性
| 名称 | 北师大版数学八年级上册第六章 数据的分析单元复习课 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 197.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-17 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
第六章 数据的分析
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
1.能用条形统计图、折线统计图、扇形统计图直观、有效地描述数据.
2.理解平均数的意义,能计算中位数、众数、加权平均数,了解它们是数据集中趋势的描述.
3.体会刻画数据离散程度的意义,会计算简单数据的方差.
4.能解释统计结果,根据结果做出简单的判断和预测,并能进行交流.
知识导航
数据的分析 平均数 算术平均数:一般的,对于n个数x1,x2,…,xn,我们把 (x1+x2+…+xn)叫做这n个数的算术平均数,简称平均数,记为x
加权平均数:若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,则
叫做这n个数的加权平均数
_
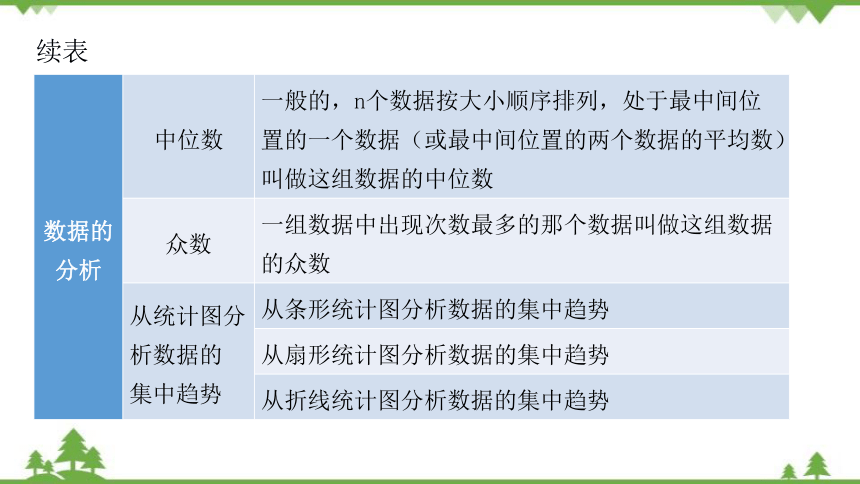
续表
数据的分析 中位数 一般的,n个数据按大小顺序排列,处于最中间位置的一个数据(或最中间位置的两个数据的平均数)叫做这组数据的中位数
众数 一组数据中出现次数最多的那个数据叫做这组数据的众数
从统计图分 析数据的 集中趋势 从条形统计图分析数据的集中趋势
从扇形统计图分析数据的集中趋势
从折线统计图分析数据的集中趋势
续表
数据的分析 数据的离散程度 极差:一组数据中最大数据与最小数据的差
方差:各个数据与平均数之差的平方的平均数,即s2= [(x1-x)2+(x2-x)2+…+(xn-x)2]
标准差:方差的算术平方根
-
-
-
1.(2020黑龙江)一组从小到大排列的数据:x,3,4,4,5(x为正整数),唯一的众数是4,则该组数据的平均数是( )
A. 3.6 B. 3.8或3.2
C. 3.6或3.4 D.3.6或3.2
2. (2020淮安)一组数据9,10,10,11,8的众数是( )
A. 10 B. 9 C. 11 D.8
专题1 平均数、中位数、众数
C
A
3.某公司招聘职员,公司对应聘者进行了面试和笔试(满分均为100分),规定笔试成绩占40%,面试成绩占60%.应聘者蕾蕾的笔试成绩和面试成绩分别为95分和90分,她的最终得分是( )
A.92.5分 B.90分 C.92分 D.95分
C
4.在九年级一次数学单元测验中,某班一个学习小组6人的成绩(单位:分)分别为:85,87,98,70,84,87,则这组数据的中位数和众数分别是( )
A.86和89 B.85和86
C.86和87 D.87和87
C
成绩/m 1.95 2.00 2.05 2.10 2.15 2.25
人数 2 3 9 8 5 3
5.在中考体育加试中,某班30名男生的跳远成绩如下表:
这些男生跳远成绩的众数、中位数分别是( )
A.2.10 m,2.05 m B.2.10 m,2.10 m
C.2.05 m,2.10 m D.2.05 m,2.05 m
C
6.在从小到大排列的五个整数中,中位数是2,唯一的众数是4,则这五个数和的最大值是( )
A.11 B.12 C.13 D.14
7. (2020乐山)某小组七位学生的中考体育测试成绩(满分40分)依次为37,40,39,37,40,38,40,则这组数据的中位数是_________.
A
39
8.在一次青年歌手演唱比赛中,10位评委给某位歌手的打分分别是:9.5,9.8,9.4,9.5,9.6,9.3,9.6,9.4,9.3,9.4,则这组数据的众数是_________.
9.4
9.红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机抽取10名同学的成绩(单位:分),收集数据如下:
(1)班:90,70,80,80,80,80,80,90,80,100;
(2)班:70,80,80,80,60,90,90,90,100,90;
(3)班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数/分 60 70 80 90 100
(1)班人数 0 1 6 2 1
(2)班人数 1 1 3 a 1
(3)班人数 1 1 4 2 2
班级 平均数/分 中位数/分 众数/分
(1)班 83 80 80
(2)班 83 c d
(3)班 b 80 80
分析数据:
根据以上信息回答下列问题:
(1)请写出表格中a,b,c,d的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩最好?请说明理由.
解:(1)由题意知a=4,b= ×(90+60+70+80+80+80+80+90+
100+100)=83,
(2)班成绩重新排列为60,70,80,80,80,90,90,90,90,100,
所以c= =85,d=90.
(2)(2)班成绩最好.理由如下:
从平均数上看三个班都一样;从中位数看,(1)班和(3)班一样是80分,(2)班最高,是85分;从众数上看,(1)班和(3)班都是80分,(2)班是90分.
综上所述,(2)班成绩最好.
1.(2020烟台)如果将一组数据中的每个数都减去5,那么所得的一组新数据( )
A. 众数改变,方差改变
B. 众数不变,平均数改变
C. 中位数改变,方差不变
D.中位数不变,平均数不变
专题2 方差、标准差
C
2. (2020辽阳)某校九年级进行了3次数学模拟考试,甲、乙、丙、丁4名同学3次数学成绩的平均分都是129分,方差分别是s2甲=3.6,s2乙=4.6,s2丙=6.3,s2丁=7.3,则这4名同学3次数学成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D.丁
A
3.某班在阳光体育活动中,测试了五位学生的一分钟跳绳成绩,得到5个各不相同的数据.在统计时,出现了一处错误:将最低成绩写得更低了,则计算结果不受影响的是( )
A.平均数 B.中位数 C.方差 D.极差
B
品种 甲 乙 丙 丁
x 24 24 23 20
s2 2.1 1.9 2 1.9
_
4.去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:kg)及方差s2如下表所示:
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是( )
A.甲 B.乙 C.丙 D.丁
B
5.已知一组数据为7,2,5,x,8,它们的平均数是5,则这组数据的方差为( )
A.3 B.4.5 C.5.2 D.6
6. (2020郴州)某5人学习小组在寒假期间进行线上测试,其成绩(单位:分)分别为:86,88,90,92,94,方差为s2=8.0,后来老师发现每人都少加了2分,每人补加2分后,这5人新成绩的方差s2新=_________.
C
8.0
18
同学 第一次 第二次 第三次 第四次 第五次
甲 90 88 92 94 91
乙 90 91 93 94 92
7.已知一组数据x1,x2,x3,…,xn的方差为2,则另一组数据3x1,3x2,3x3,…,3xn的方差为_________.
8.下表是甲、乙两名同学近五次数学测试(满分均为100分)的成绩(单位:分)统计表:
根据上表数据,成绩较好且比较稳定的同学是_________.
乙
9.甲、乙两名队员参加射击训练,成绩分别被制成如图Z6-1所示两个统计图.
根据以上信息,整理分析数据如下表:
队员 平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 1.2
乙 7 b 8 c
(1)计算出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
解:(1)甲的平均成绩
a= =7(环).
因为乙射击的成绩从小到大重新排列为3,4,6,7,7,8,8,8,9,10,
所以乙射击成绩的中位数b= =7.5(环).
其方差c= ×[(3-7)2+(4-7)2+(6-7)2+2×(7-7)2+3
×(8-7)2+(9-7)2+(10-7)2]= ×(16+9+1+3+4+9)=4.2.
(2)从平均成绩看甲、乙二人的成绩相等均为7环;从中位数看甲射中7环以上的次数少于乙;从众数看甲射中7环的次数最多而乙射中8环的次数最多;从方差看甲的成绩比乙的成绩更稳定.
综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能性更大.
谢 谢
第六章 数据的分析
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
1.能用条形统计图、折线统计图、扇形统计图直观、有效地描述数据.
2.理解平均数的意义,能计算中位数、众数、加权平均数,了解它们是数据集中趋势的描述.
3.体会刻画数据离散程度的意义,会计算简单数据的方差.
4.能解释统计结果,根据结果做出简单的判断和预测,并能进行交流.
知识导航
数据的分析 平均数 算术平均数:一般的,对于n个数x1,x2,…,xn,我们把 (x1+x2+…+xn)叫做这n个数的算术平均数,简称平均数,记为x
加权平均数:若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,则
叫做这n个数的加权平均数
_
续表
数据的分析 中位数 一般的,n个数据按大小顺序排列,处于最中间位置的一个数据(或最中间位置的两个数据的平均数)叫做这组数据的中位数
众数 一组数据中出现次数最多的那个数据叫做这组数据的众数
从统计图分 析数据的 集中趋势 从条形统计图分析数据的集中趋势
从扇形统计图分析数据的集中趋势
从折线统计图分析数据的集中趋势
续表
数据的分析 数据的离散程度 极差:一组数据中最大数据与最小数据的差
方差:各个数据与平均数之差的平方的平均数,即s2= [(x1-x)2+(x2-x)2+…+(xn-x)2]
标准差:方差的算术平方根
-
-
-
1.(2020黑龙江)一组从小到大排列的数据:x,3,4,4,5(x为正整数),唯一的众数是4,则该组数据的平均数是( )
A. 3.6 B. 3.8或3.2
C. 3.6或3.4 D.3.6或3.2
2. (2020淮安)一组数据9,10,10,11,8的众数是( )
A. 10 B. 9 C. 11 D.8
专题1 平均数、中位数、众数
C
A
3.某公司招聘职员,公司对应聘者进行了面试和笔试(满分均为100分),规定笔试成绩占40%,面试成绩占60%.应聘者蕾蕾的笔试成绩和面试成绩分别为95分和90分,她的最终得分是( )
A.92.5分 B.90分 C.92分 D.95分
C
4.在九年级一次数学单元测验中,某班一个学习小组6人的成绩(单位:分)分别为:85,87,98,70,84,87,则这组数据的中位数和众数分别是( )
A.86和89 B.85和86
C.86和87 D.87和87
C
成绩/m 1.95 2.00 2.05 2.10 2.15 2.25
人数 2 3 9 8 5 3
5.在中考体育加试中,某班30名男生的跳远成绩如下表:
这些男生跳远成绩的众数、中位数分别是( )
A.2.10 m,2.05 m B.2.10 m,2.10 m
C.2.05 m,2.10 m D.2.05 m,2.05 m
C
6.在从小到大排列的五个整数中,中位数是2,唯一的众数是4,则这五个数和的最大值是( )
A.11 B.12 C.13 D.14
7. (2020乐山)某小组七位学生的中考体育测试成绩(满分40分)依次为37,40,39,37,40,38,40,则这组数据的中位数是_________.
A
39
8.在一次青年歌手演唱比赛中,10位评委给某位歌手的打分分别是:9.5,9.8,9.4,9.5,9.6,9.3,9.6,9.4,9.3,9.4,则这组数据的众数是_________.
9.4
9.红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机抽取10名同学的成绩(单位:分),收集数据如下:
(1)班:90,70,80,80,80,80,80,90,80,100;
(2)班:70,80,80,80,60,90,90,90,100,90;
(3)班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数/分 60 70 80 90 100
(1)班人数 0 1 6 2 1
(2)班人数 1 1 3 a 1
(3)班人数 1 1 4 2 2
班级 平均数/分 中位数/分 众数/分
(1)班 83 80 80
(2)班 83 c d
(3)班 b 80 80
分析数据:
根据以上信息回答下列问题:
(1)请写出表格中a,b,c,d的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩最好?请说明理由.
解:(1)由题意知a=4,b= ×(90+60+70+80+80+80+80+90+
100+100)=83,
(2)班成绩重新排列为60,70,80,80,80,90,90,90,90,100,
所以c= =85,d=90.
(2)(2)班成绩最好.理由如下:
从平均数上看三个班都一样;从中位数看,(1)班和(3)班一样是80分,(2)班最高,是85分;从众数上看,(1)班和(3)班都是80分,(2)班是90分.
综上所述,(2)班成绩最好.
1.(2020烟台)如果将一组数据中的每个数都减去5,那么所得的一组新数据( )
A. 众数改变,方差改变
B. 众数不变,平均数改变
C. 中位数改变,方差不变
D.中位数不变,平均数不变
专题2 方差、标准差
C
2. (2020辽阳)某校九年级进行了3次数学模拟考试,甲、乙、丙、丁4名同学3次数学成绩的平均分都是129分,方差分别是s2甲=3.6,s2乙=4.6,s2丙=6.3,s2丁=7.3,则这4名同学3次数学成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D.丁
A
3.某班在阳光体育活动中,测试了五位学生的一分钟跳绳成绩,得到5个各不相同的数据.在统计时,出现了一处错误:将最低成绩写得更低了,则计算结果不受影响的是( )
A.平均数 B.中位数 C.方差 D.极差
B
品种 甲 乙 丙 丁
x 24 24 23 20
s2 2.1 1.9 2 1.9
_
4.去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:kg)及方差s2如下表所示:
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是( )
A.甲 B.乙 C.丙 D.丁
B
5.已知一组数据为7,2,5,x,8,它们的平均数是5,则这组数据的方差为( )
A.3 B.4.5 C.5.2 D.6
6. (2020郴州)某5人学习小组在寒假期间进行线上测试,其成绩(单位:分)分别为:86,88,90,92,94,方差为s2=8.0,后来老师发现每人都少加了2分,每人补加2分后,这5人新成绩的方差s2新=_________.
C
8.0
18
同学 第一次 第二次 第三次 第四次 第五次
甲 90 88 92 94 91
乙 90 91 93 94 92
7.已知一组数据x1,x2,x3,…,xn的方差为2,则另一组数据3x1,3x2,3x3,…,3xn的方差为_________.
8.下表是甲、乙两名同学近五次数学测试(满分均为100分)的成绩(单位:分)统计表:
根据上表数据,成绩较好且比较稳定的同学是_________.
乙
9.甲、乙两名队员参加射击训练,成绩分别被制成如图Z6-1所示两个统计图.
根据以上信息,整理分析数据如下表:
队员 平均成绩/环 中位数/环 众数/环 方差
甲 a 7 7 1.2
乙 7 b 8 c
(1)计算出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
解:(1)甲的平均成绩
a= =7(环).
因为乙射击的成绩从小到大重新排列为3,4,6,7,7,8,8,8,9,10,
所以乙射击成绩的中位数b= =7.5(环).
其方差c= ×[(3-7)2+(4-7)2+(6-7)2+2×(7-7)2+3
×(8-7)2+(9-7)2+(10-7)2]= ×(16+9+1+3+4+9)=4.2.
(2)从平均成绩看甲、乙二人的成绩相等均为7环;从中位数看甲射中7环以上的次数少于乙;从众数看甲射中7环的次数最多而乙射中8环的次数最多;从方差看甲的成绩比乙的成绩更稳定.
综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能性更大.
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
